基于WIFI的位置指纹参考节点密度与定位精度关系研究
2019-07-09左泽谦潘军蒋立军邢立新孙也涵仲伟敬
左泽谦,潘军,蒋立军,邢立新,孙也涵,仲伟敬
1. 吉林大学 地球探测科学与技术学院,长春 130026;2.西安卫星测控中心 第一活动站,陕西 渭南 714000
0 引言
室内定位技术是通过无线局域网络进行用户定位,随着WIFI(Wireless Fidelity无线保真)定位技术的成熟,基于RSSI的WIFI室内定位技术与其他定位技术相比,无需添加额外的硬件设备且设备简易、价格实惠,具有广泛的应用价值[1-2],因此深受研究者们青睐。
基于位置指纹的室内定位是WIFI定位技术的一大分支[3-4],原理可分为两个阶段:离线和在线阶段,定位过程包含采集AP(Access Point)发射的无线信号RSSI(Received Signal Strength Indicator接收信号强度)建立离线数据库、测量待测节点在线RSSI数据和指纹匹配定位。为了提高基于位置指纹的室内定位精度,前人从离线数据库参考节点的RSSI滤波、RSSI采集方向、参考节点内在联系等方面进行研究。陶为戈等[5]通过中值、均值、高斯三种混合滤波的算法提高RSSI稳定性和准确性;赵大龙等[6]选择卡尔曼和线性插值的方法对RSSI进行滤波;毕京学等[7]从采集数据时人体对信号干扰导致衰减方面入手,提出一种全向指纹库的定位方法,削弱用户朝向引起的信号强度差异;王怡婷等[8]提出将参考节点层次聚类的方法,明确参考节点聚类个数,缩小了定位范围,减小定位误差;刘志鹏等[9]提出一种在手持设备的定位系统中增加位置指纹特征的改进型定位方法,以提高定位精度。Peng et al.[10]提出一种基于空间变异理论的位置指纹库建立方法,该方法将离线阶段采集的RSSI值分解为趋势项和随机项,根据信号传播模型和克里金法实现在少量参考点采集 RSSI值建立位置指纹库。
目前,已有研究在离线数据库信号滤波、参考节点采集方式、参考节点相关性等方面提出改进方法,用以减小误差。但是缺少从待测节点与参考节点位置关系原理推导出发,对参考节点密度与定位精度相关关系进行研究。因此,本文从参考节点与待测节点理论关系出发,采取建立正方形、三角形和六边形3种不同参考节点排布方式的计算机拟合方法,研究理想环境下不同密度参考节点对定位精度的影响,并以正方形排布方式为例进行实际验证,探究参考节点密度与定位精度关系。
1 参考节点密度与定位精度关系原理分析
位置指纹室内定位可通过在线采集待测节点的RSSI值与离线数据库中参考节点RSSI进行相似度比较,选择与待测节点最相似的一个或多个参考节点作为定位依据,对选取参考节点的坐标采用加权算法进行定位。因此可以推断,参考节点的坐标信息及分布状态决定最终定位结果,待测节点的理论位置应位于与其最相似的参考节点组成的N边形内。为探究参考节点与待测节点关系,本文从待测点与2个参考节点、3个参考节点组合的图形位置关系进行原理分析,并通过挖掘内在联系推广至待测节与N个参考节点位置关系。
1.1 待测节点与2个参考节点所组成图形位置关系
建立两个参考节点与待测节点位置关系(图1),其中A、B两点为与待测节点x相似度最高的两个参考节点,点A坐标为(X1,Y1),

图1 两点加权定位示意图Fig.1 Two-point weighted location diagram
点B坐标为(X2,Y2),待测点X坐标为(X,Y)。其中:
待测点X的坐标为:
X=K1×X1+K2×X2
Y=K1×Y1+K2×Y2
(1)
K1+K2=1
(2)
直线AB的斜率为:
(3)
直线AX的斜率为:
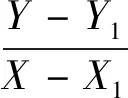
(4)
kAB=kAX
(5)
由式(5)知,点直线AX的斜率与直线AB的斜率相等,所以X在直线AB上,即待测节点在相似参考节点所组成的图形内。
1.2 待测节点与3个参考节点所组成图形位置关系
建立三个参考节点与待测节点位置关系(图2),其中点A、B、C为与待测点x最相似的3个参考节点,坐标分别为(X1,Y1)、(X2,Y2)、(X3,Y3),待测节点X坐标(X,Y),辅助点D坐标(X4,Y4)。

图2 三点加权定位示意图Fig.2 Three-point weighted location diagram
待测节点X的坐标为:
(6)
(7)
点D的坐标为:
(8)
其中:
(9)
以待测点X横坐标X为例证明:
(10)
式(10)整理可得:
(11)
由式(1)和式(11)可知:
(12)
由式(7)和式(12)可知:

(13)
即式(13)待测节点X横坐标表达式等价于式(6)中横坐标表达式。待测点X纵坐标同理可证。
对比式(13)待测节点X横坐标表达式与式(6)中横坐标表达式可知,分步加权效果与总体加权效果等效。由于辅助点D在直线AB内,点X在直线AD内,因此待测点X位于参考节点A、B、C所组合成的图形内。对于多个相似参考节点所组成图形而言,任意一个多边形内三个顶点可以组合成一个三角形,而通过3个参考节点加权计算的待测节点在三角形内,所以推论待测节点也在该多边形内。
通过论证待测点计算结果与参考点所组成图形关系,认为当参考节点间距减小即参考节点密度增大,参考节点所组合的图形面积变小,定位误差范围减小,因此定位精度提高。
2 理论模型仿真与结果
为了验证参考节点密度与定位精度的影响,本文建立正方形、三角形和六边形三种参考节点排布方式的离线数据库,将参考节点与待测节点RSSI值及距离d理论化,讨论在相同环境下三种排布方式不同参考节点密度对定位精度的影响。
2.1 离线数据库建立
以C++为开发平台,设计对数—常态分布模型[11]为RSSI信号模型,模拟场地为60 m×60 m的方形区域。
RSSI=A-10nlg(d)
(14)
其中,环境因子A和n分别为-23和2,参考节点按照三角形分布、正方形分布和六边形分布建立不同密度离线数据库(图3,4,5),每种排布方式的参考节点间距均为0.5 m、1 m、2 m、3 m、4 m、 5 m 6种。 随机选取7 000个待测节点, 并利用式(14)计算待测节点接收4个AP的理论RSSI值。

图3 三角形分布示意图Fig.3 Sketch map of triangular distribution
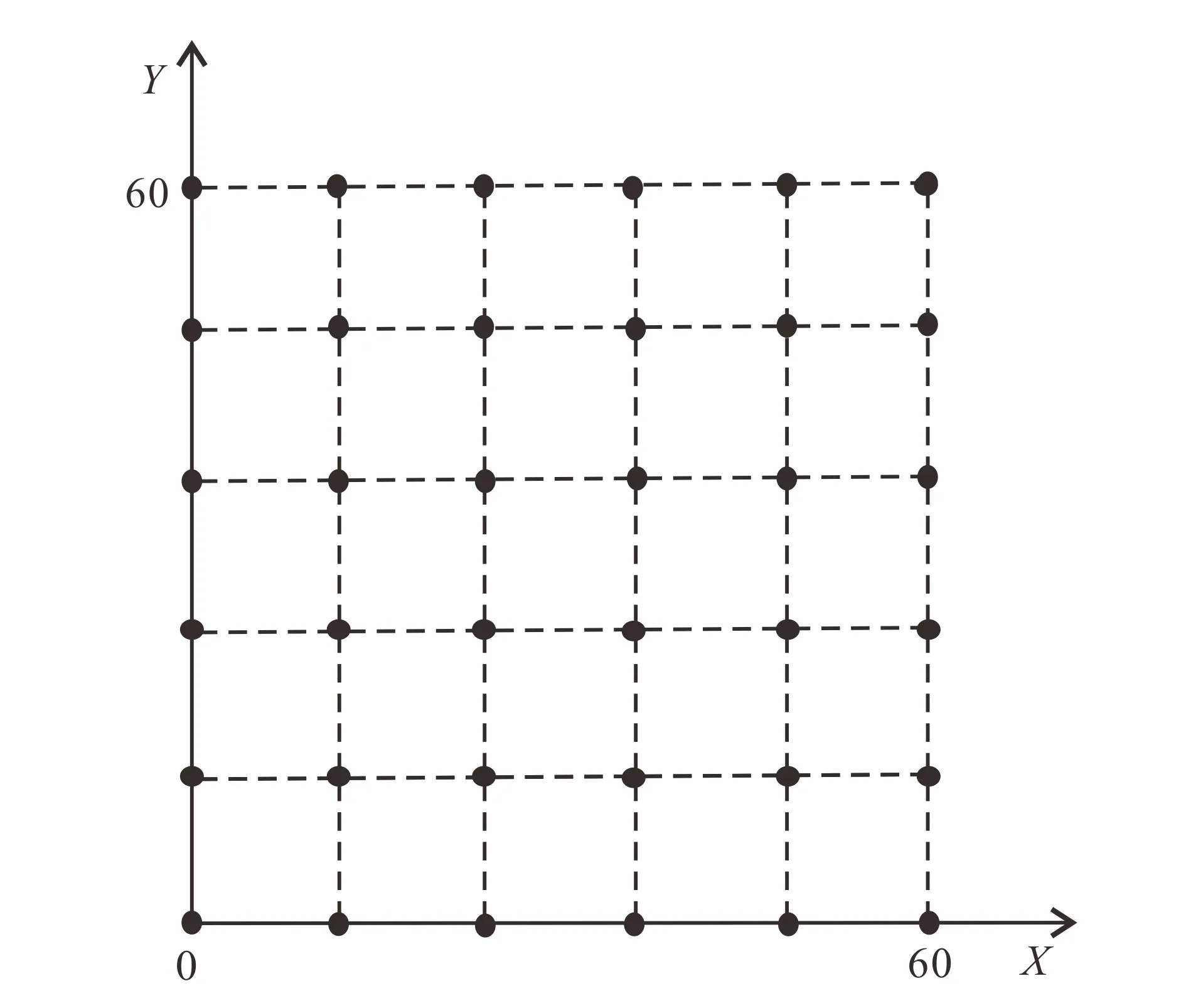
图4 正方形分布示意图Fig.4 Sketch map of square distribution
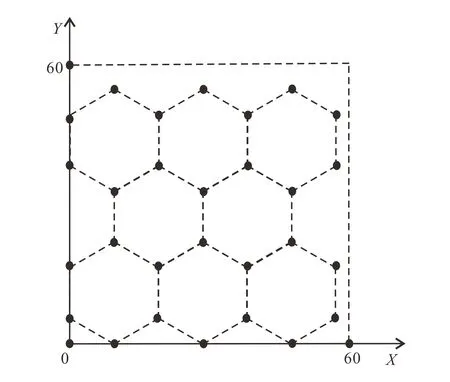
图5 六边形分布示意图Fig.5 Sketch map of hexagon distribution
2.2 加权K近邻算法
基于位置指纹定位算法中,常用的算法有近邻算法(NN nearest neighbor)、K近邻算法(KNN k-nearest neighbor)和加权K近邻算法(WKNN weighted k-nearest neighbor)[12]。WKNN算法是学者们在近邻算法(NN)和K近邻算法(KNN)算法基础上提出的。WKNN算法过程为计算未知节点与参考节点间的欧式距离,选取欧氏距离的倒数作为对应参考节点的权重系数,将前K个欧式距离最小的参考节点对应坐标与相应权重系数相乘并相加,作为最终未知节点坐标。表达式为:

(15)
其中,Di为待测节点与第i个参考节点欧式距离,δ为较小的系数,避免出现分母为0的情况。
2.3 理论实验结果
本文选择计算坐标与实际坐标的误差作为定位精度的评判标准,统计正方形分布、三角形分布和六边形3种参考节点排布方式下不同密度的平均定位误差(表1),并计算回归方程(图6,7,8)。误差公式为:
(16)

表1 三种排布方式定位精度结果

图6 正方形分布回归方程Fig.6 Regression equation of square distribution

图7 三角形分布回归方程Fig.7 Regression equation of triangular distribution

图8 六边形分布回归方程Fig.8 Regression equation of hexagon distribution
通过正方形、三角形和六边形三种参考节点排布方式的理论实验仿真,平均误差随参考节点密度减小而增大,定位精度与参考节点密度存在关系。其中三种排布方式参考节点密度与定位精度回归方程为:正方形:y=0.152x-0.135 3;三角形:y=0.144 3x-0.13;六边形:y=0.242x-0.242。
3 参考节点密度与定位精度实际实验
3.1 定位过程
实验场地为吉林大学虚拟仿真实验教学中心一楼12 m×10 m的矩形空旷环境(图9),实验设备为4台小米路由器(型号MT7628A)SONY笔记本一台(型号SVE151T11E),信号采集软件Homedale。研究在相同环境下,相同待测节点在2 m、3 m、4 m、5 m 4种不同参考节点密度下定位精度的比较。

图9 实验场地Fig.9 Experimental site
(1)实验场地内布设4个AP,以场地左下角为坐标原点,4个AP坐标分别为(0.5,0)、(0.5,8)、(11.5,0)和(11.5,8)。
(2)从原点起每隔2 m间距设置一个参考节点,遍历整个实验区域,共计42个。
(3)手持电脑站在预先布设的参考节点上,通过软件Homedale采集并记录每个参考节点接收4个AP的RSSI值(RSSIAP1i,RSSIAP2i,RSSIAP3i,RSSIAP4i)(i=1,2,3,…,42),每点采集时长2 min,采集频率1次/s。
(4)将42个参考节点采集数据选用均值与众数混合方法进行滤波,滤波后的数据作为最终结果同对应物理坐标(X参,Y参)录入2 m间距参考节点离线数据库。
(17)
(5)重复步骤(3)(4),建立3 m间距、4 m间距和5 m间距参考节点离线数据库。
(6)待测节点采集。在该矩形场地内随机选取25个待测节点,记录每个待测节点实际物理坐标(X待,Y待),采集并滤波每个待测节点4个AP的RSSI值,方法同参考节点。
(7)遍历计算待测节点与参考节点欧式距离,选取最相似的4个参考节点,使用WKNN算法进行待测节点定位,并利用式(16)计算4种不同参考节点密度下的定位误差。
3.2 实验结果
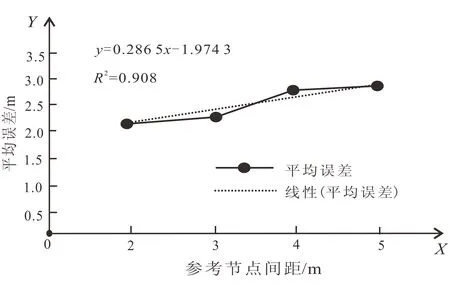
图10 实际实验结果Fig.10 Results of practical experiment
计算4种不同参考节点密度下的平均定位误差(图10),2 m间距的参考节点平均定位误差最小,5 m间距的参考节点平均定位误差最大,回归方程为:y=0.286 5x-1.974 3,定位精度遵循参考节点密度越大精度越高的规律。
4 结论
(1)不同参考节点密度下的定位精度不同,且定位精度伴随参考节点密度的增加而提高。
(2)计算不同密度下的定位精度可知,定位精度与参考节点密度呈显著正相关线性关系。
