一种Fibonacci迭代的差分进化生物地理学优化算法
2019-07-09郑夏,马良
郑 夏,马 良
(上海理工大学 管理学院,上海 200093)
1 引 言
目前的智能优化算法已开始大量用于解决工程优化问题,其基本思想是通过对自然界生物规律的研究来构建仿生群算法.近年来,广泛应用到工程和科研领域的仿生算法有:遗传算法(Genetic Algorithm,GA)[1]、蚂蚁算法(Ant Colony Optimization,ACO)[2]、粒子群算法(Particle Swarm Optimization,PSO)[3]、果蝇优化算法(Fruit fly Optimization,FOA)[4]等.生物地理学优化算法(biogeography-based optimization,BBO)是Simon[5]在2008年提出的一种新的基于生物迁移规律的全局优化仿生算法,可以应用于一些较为复杂的工程优化问题中.因此,对BBO算法的理论和应用研究具有重要的学术和工程价值.
BBO算法的基本思想不同于其他智能优化算法,其信息的相互流通是由各个栖息地之间的物种的迁移来完成,信息的共享以及栖息地适应性的不断提高均是由迁移过程中适当地调整迁入率和迁出率、迁移策略、迁移时间间隔、迁移拓扑结构来实现的,进而得到求解问题的最优解.在进化过程中的原始种群(指栖息地)不会消失,种群适应度通过种群的迁移来提高,反过来种群的迁移率大小又由种群的适应度来决定,这是BBO算法最大的特点,因此其结构简单且效率较高.但是,由于受种群栖息地影响,算法在搜索过程中容易陷入局部最优,且变异算子可能会影响算法的收敛速度.由此,一些改进的BBO算法陆续被提出用于改善其算法性能.文献[6]总结了BBO算法的理论分析、改进的BBO算法及混合算法的应用.文献[7]通过改进的动态选择迁出地来优化迁入策略,增强了算法的全局搜索能力.文献[8]为了增强算法搜索解的能力,进一步提高收敛速度和精度,提出了一种混合迁移策略.文献[9]通过测试函数表明了所提出的的6种新的生物迁移策略有效提高了算法性能.文献[10]为提高算法在特定问题上的性能提出一种Markov精英选择策略.综上所述,大多数改进BBO算法性能的提高均是通过改进迁移算子来实现.
差分进化算法是一种从随机群体开始进行选择、杂交、变异操作的随机并行直接搜索算法,在种群不断迭代的过程中通过淘汰劣质个体,保留适应度值较高的优良个体来逐步逼近最优解,该算法原理简单,控制参数较少,是一种性能优异,鲁棒性强,收敛速度较快的全局优化算法.近些年已有不少关于差分进化算法的研究[11-15].本文在基本BBO算法的主要流程上,首先通过基于Fibonacci数列的迭代思想消除种群内部的重复性来提高种群精度提出了一种改进的IBBO算法,然后在此基础上引入全局搜索能力较强的差分进化算法来改进IBBO算法中的变异算子,提出一种改进的IDEBBO算法,最后针对8个基准测试函数以及与FOA、DE、基本BBO算法、IBBO算法进行实验比较,结果表明,IDEBBO算法的收敛效果最好.
2 BBO算法
生物种群“栖息地”[5],适宜度指数(HSI,Habitat Suitability Index)随栖息地的不同而不同,其如何影响栖息地的种群迁移和分布是由栖息地的迁入率和迁出率来描述的:当栖息地承载的种群数量较大时HSI相对较高,但是随着该地种群迁入的增多,所能容纳的种群量趋于饱和,则迁出率随之增高,部分种群会向邻近栖息地迁移以增加种群个体拥有的单位资源,原栖息地的迁入率随之下降;当栖息地承载的种群数量较少时HSI相对较低,迁入率也由于该地种群数量稀疏而增高,栖息地适宜度的向量(SIV,Suitable Index Vector)是由与HSI有关的特征变量包括:生物多样性、地质多样性、气候多样性、植被多样性和降雨量等因素形成的,其中,SIVs(Suitable Index Variables)是指具体的每一个适宜度变量.由此可知,HSI会随着与其成正比的由于新种群的迁入所引起的生物多样性的提高而提高,但若HSI仍然较低时会引起该栖息地的种群最终趋于灭绝或迁移于别的栖息地.可以看出,当栖息地的HSI较低时所引起的生物种群的动态变化比HSI较高时更加复杂.
2.1 迁移操作
迁移是一种概率性运算,通过分享不同迁移方案之间的特性来修改每一个方案Hi.迁移运算的思想是基于生物地理学中的迁移概念,表明了种群在不同栖息地之间的移动.方案Hi表示向栖息地迁入,其相对应的迁入率为λi.方案Hj表示从栖息地迁出,其相对应的迁出率为μj,Hi(SIVw)表示栖息地Hi的第w个SIV.由此可知,一个栖息地方案被选为迁入或迁出的概率依赖于它的迁入率λi或迁出率μj.因此迁移过程可以表示为:
Hi(SIVw)←Hj(SIVw)
(1)
迁入率λi,迁出率μj和一个栖息地种群之间的平衡关系如图1[10]所示.正如所提到的,较高HSI栖息地方案的特点是倾向于迁出到较低HSI栖息地方案.通过种群的渐增,迁入率减小,迁出率增大的现象.图中E和I分别代表迁出率和迁入率的最大值,Smax表示一个栖息地所能承载的种群最大值,S0表示迁入率和迁出率相等的平衡点.虽然该图中迁入和迁出为线性表示,需要时它们也可以用其他曲线来表示.应注意的是,E和I通常设值为1.公式(1)表明一个迁移策略的特征或SIV和另一个迁移策略的特征或SIV之间是如何在迁移过程中进行调整的.策略的一个SIV表示其一个特征并且被当做一个搜索变量使用.
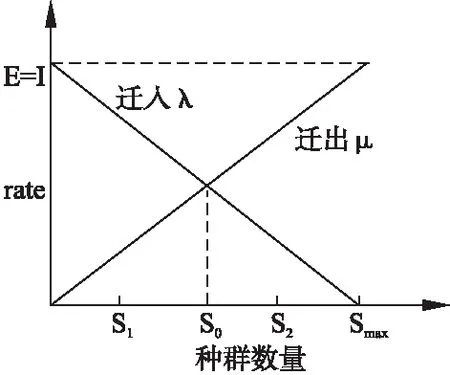
图1 BBO算法中种群迁移模型Fig.1 Species migration model in the BBO algorithm
因此,一组所有可能的适宜度变量SIVs被看作一个迁移策略的搜索空间.
为每一个迁移方案Hj计算完适宜度指数HSI后,可用公式(2)和公式(3)分别来评估迁入率λi和迁出率μj,即这两个比率是该迁移方案的适应度函数或HSI.由于根据生物地理学知识,一个有较高HSI的迁移方案中的SIVs趋向于向较低HSI迁移方案中迁移,这是因为,较高HSI的迁移方案中有较高的迁出率μj,较低的迁入率λi,较低HSI的迁移方案中有较高的迁入率λi,较低的迁出率μj.
(2)
(3)
公式(2)和公式(3)中,ki代表根据它们的HSIs对所有栖息地进行分类后的第i个栖息地的等级,n代表种群的规模.由此可知,由于更多的HSI代表了更好的迁移方案,更多的ki代表了这个更好的迁移方案.因此,第一个迁移方案是最坏的,第n个方案是最好的.另一个需要计算的参数是在栖息地中存在S个种群的可能性,用Ps来表示.由于对时间t到t+Δt之间的变化过程进行建模,以下三个状态中会有一个发生,因此该参数由公式(4)得到:
Ps(t+Δt)=Ps(t)(1-λsΔt-μsΔt)+
Ps-1λs-1Δt+Ps+1μs+1Δt
(4)
1)在时间t有S个种群,且在时间t到t+Δt之间无种群再迁入或迁出.
2)在时间t有S-1个种群,且在时间t到t+Δt之间只有一个种群的迁入.
3)在时间t有S+1个种群,且在时间t到t+Δt之间只有一个种群的迁出.
(5)
(6)
由上可知,迁移操作已完成.
2.2 突变操作
BBO算法中,突变是一种概率运算符,它用于根据其存在的先验概率Pi来修改迁移方案中一个或多个随机选择的SIV,该算法中,根据求解概率Pi计算出突变概率mi如公式(7)所示,因此,突变概率和求解概率是成比例的.
(7)
其中,mmax是突变率的最大值,Pi为栖息地包含i个种群的概率,Pmax=max(Pk).突变操作可以由公式(8)表示.
Hi(SIVw)←lbw+rand*(ubw-lbw)
(8)
其中,Hi表示突变栖息地,ubw和lbw分别是指该栖息地第w个SIV的上、下边界值.
3 IDEBBO算法
基本BBO算法在优化高维复杂问题过程中,若最优个体陷入了局部最优解,整个种群会因此进入早熟收敛,从而降低了优化效率和求解精度.因此可首先通过Fibonacci数列的迭代消除种群内部重复性个体来提高求解精度,从而对BBO算法进行改进,得到IBBO算法,然后再引入全局搜索能力较强的差分进化算法来改进IBBO算法中的变异算子,得到一种改进型的IDEBBO算法.
3.1 IBBO算法设计
3.1.1 消除重复性设计思想
Fibonacci数列的递归思想中产生的大量重复计算,重复计算会消耗算法执行的有效时间,如求解F(n),必须先计算F(n-1)和F(n-2),计算F(n-1)和F(n-2),又必须先计算F(n-3)和F(n-4)…以此类推,直至必须先计算F(1)和F(0),然后逆推得到F(n-1)和F(n-2)的结果,从而得到F(n)要计算很多重复的值,在时间上造成了很大的浪费算法的时间复杂度随着N的增大呈现指数增长,时间的复杂度为O(2^n),即2的n次方.重复计算会导致种群内部出现相同的SIV个体,即冗余的相同值,占用有效的存储空间,导致算法空间复杂度增大.
Fibonacci数列的迭代思想中算法的时间复杂度与n成正比,从(n>2)开始计算,用变量的旧值递推新值,如F(n)=F(n-1)+F(n-2),F(n-1)=F(n-2),F(n-2)=F(n),则算法的时间复杂度为O(n),是不断地用变量的旧值递推新值的过程,从而达到消除种群内部重复性SIV个体的目的,提高了算法求解精度.因此引入Fibonacci数列的迭代思想可以减小算法的时间复杂度和空间复杂度.
3.1.2 IBBO设计核心操作
Step 1.迁移操作
令N表示种群规模,d表示维度的数量,rand表示0到1之间均匀分布的随机实数,若rand<λi,根据迁出率用轮盘赌的方式选择一个迁出栖息地Hj,执行公式(1)来更新Hi(SIVw).
Step 2.突变操作
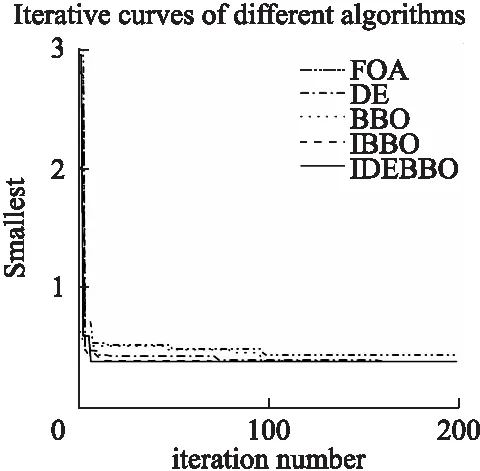
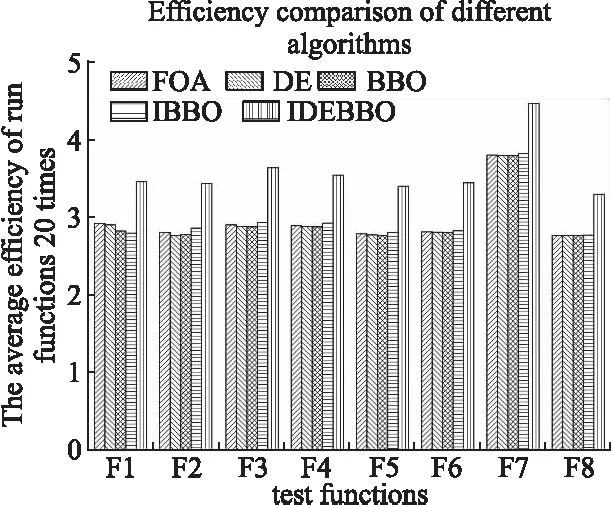
令N表示种群规模,d表示维度的数量,rand表示0到1之间均匀分布的随机实数,执行公式(7)计算变异率mi,若rand Step 3.消除重复性个体操作 若将所有迁入栖息地的SIVs根据HSI排序的序列记作s1,将所有迁出栖息地的SIVs根据HSI排序的序列记作s2.则最后为消除种群内部重复性个体,需对isequal(s1,s2)进行判断,若满足则重新赋值后的迁出栖息地种群表示为: w1=ceil(s2*rand) (9) Hj(SIVw1)=(1-rand)*min(s1)+rand*max(s2) (10) min(s1)=max(s2) (11) max(s2)=Hj(SIVw1) (12) 式中w1指栖息地中第w1个SIV.该赋值在循环过程中,充分利用了不断用旧值递推新值得过程,使得算法效率增高.对相同的种群个体,根据Fibonacci数列的迭代思想重新赋值,执行公式(9)~公式(12),从而消除重复SIV个体,提高求解精度. 3.1.3 IBBO算法伪码 如表1所示为IBBO伪代码. 表1 IBBO伪代码 算法1.IBBO算法Steps:1.Parameterseeting:E=1,I=1,mmax=1,Pop.size=50,Num.itera-tion=2002.Initialization:Generatinghabitatsassizeaspopulationsize3.Populationevaluation:evaluationhabitats4.SortthepopulationaccordingtotheHSIofthehabitatsincreasingly5.fori=1:Num.iteration6. Calculateλi,μi,Pi&miaccordingtohabitat′srank7. forj=1:Pop.size8. GenerateRand∈[0,1]9. IfRand<=λi10. Hi(SIV)=ChooseahabitatrandomlythroughaRoulettgewheelofμ(μ1,μ2,…,μn)11. ExecutemigrationoperatorHi(SIVw)←Hj(SIVw)12. Else13. Thehabitatskeepsunchanged14. Endif15. GenerateRand∈[0,1]16. IfRand<=mi17. Executemutationoperator18. RecodethesamepopulationbasedontheiterativethroughtofFibonaccisequence18. Else19. Thehabitatkeepsunchanged20. Endif21. Endfor22.Calculateλi,μi,Pi&miaccordingtohabitat′srank23.Endfor 3.2.1 差分变异算子设计思想 差分进化DE是一种鲁棒性较强的进化算法[12],通过使用当前种群的距离和方向信息来指引进一步搜索,其差分操作提供了较强的全局搜索能力.因此根据该思想改进IBBO算法的变异算子为更高效的差分变异操作.如公式(13)所示: Hi(SIVw)←Hi(SIVw)+δ*(Hbest(SIVw)- Hi(SIVw)+Hx(SIVw)-Hy(SIVw)) (13) 其中,Hx,Hy(x,y∈[1,n]且x≠y≠i)表示随机选择的两个栖息地.权重δ为0和1之间均匀分布的随机实数,Hbest为当前迭代中HSI最好的栖息地.由上式可知,突变操作栖息地Hi的SIV受其自身和其它三个不同栖息地影响.通过Hbest与Hi之间和Hx与Hy之间的差分运算,得到两个差分值,将这两个差分值乘权重系数δ,并将获得权重的两个差分值加到Hi(SIVw),因此Hi(SIVw)可以接受更加多样的信息来增加种群多样性.另外,由于多样化信息的一部分来自于Hbest,因此更加有利于Hi在搜索空间中向Hbest移动. 与BBO算法中原始的突变操作对比发现,改进后的差分变异操作提高了全局搜索能力,并且可以在搜索空间中引导突变操作向当前最好的栖息地移动,一定程度上预v 防了较为优的迁移方案被破坏的情况. 3.2.2 IDEBBO算法伪码 如表2所示为IDEBBO算法之差分变异操作. 表2 IDEBBO算法之差分变异操作 算法2.IDEBBO算法之差分变异操作Steps:1.GeneratetheinitialpopulationPop.size=50,Num.iteration=2002.Initialization:Generatinghabitatsassizeaspopulationsize3.Populationevaluation:evaluationhabitats4.SortthepopulationaccordingtotheHSIofthehabitatsincreasingly5.fori=1:Num.iteration6. Calculateλi,μi,Pi&miaccordingtohabitat′srank7. PerformEq.(7)tocalculatethemutationratemi8. forw=1toddo9. ifrand 上述算法在Matlab2016b中进行编程并作计算实验,采用8个经典的测试函数进行仿真测试.通过与FOA、DE、基本BBO算法、IBBO算法的对比验证,表明本文改进算法IDEBBO的高效性.由于智能优化算法的思想是模拟生物进化过程且具有一定的随机性.因此实验分别运行算法各20次来降低随机因素干扰,取其平均值来比较算法寻优精度及算法效率. 由于暂无严格标准的理论依据来规范BBO算法中涉及的参数设置,且考虑到对比的公平性,对比算法均须采用一致的参数设置,因此,本文经反复多次实验所得经验值来设置算法的参数如下:栖息地的最大迁入率I和最大迁出率E均设置为1,栖息地SIVs的最小迁入率和最大迁入率为0和1,最大迁移率pmodify设置为1,精英个数为3,最大变异率C为0.2,差分因子δ为0.6. 8个标准测试函数的表达式、搜索空间及理论最优值如表3所示(其中,x′表示该函数在搜索空间里取得最优值的位置不唯一): 表中函数f1是多个余弦波调制成的多峰函数,函数f2是单极值单峰函数,函数f3和f5均为搜索空间里分布大量局部极值且较容易陷入局部最优的多峰多极值函数,f4函数是取值区间趋于平坦且较难搜索到全局最优值的病态单峰二次函数,f6函数是具有强烈的震荡性且较难找到全局最优值的复杂二维函数,f7函数在其搜索区间里有若干局部极小值和3个全局最优值,f8是为使优化很难找到最优值而特意设计了许多个虚假局部最低值的函数.综上,8个函数均为适合检验算法全局搜索能力和跳出局部最优避免早熟之收敛能力的复杂非线性经典测试函数. 表3 标准测试函数 函数名函数表达式维度探索空间理论最优值Ackleyf1(x)=20+e-20exp(-151n∑ni=1x2i)-exp(1n∑ni=1cos(2πxi))30[-30,30]f1(0,…,0)=0Spheref2(x)=∑ni=1x2i30[-100,100]f2(0,…,0)=0Griewankf3(x)=14000∑Di=1(x2i)-ΠDi=1cos(xii)+130[-600,600]f3(0,…,0)=0Rosenbrockf4(x)=∑D-1i=1[100(xi+1-x2i)2+(xi-1)2]30[-100,100]f4(0,…,0)=0Rastriginf5(x)=∑ni=1(x2i-10cos(2πxi)+10)30[-5.12,5.12]f5(0,…,0)=0Schafferf6(x)=sin2x21+x22-0.5[1+0.001(x21+x22)]2-0.52[-100,100]f6(0,0)=-1Braninf7(x)=(x2-54π2x21+5πx1-6)2+10(1-18π)cos(x1)+1030[-5,15]f7(x′)=0.3979Schwefelf8(x)=418.9829×D-∑Di=1xisin(|xi|1/2)30[-500,500]f8(420.96,…,490.96)=0 分别用FOA、DE、基本BBO算法、IBBO算法和IDEBBO算法对上述选取的8个标准测试函数进行优化比较,且各运行5个算法20次来降低随机因素干扰,所得到的最优值、最差值、均值、标准差比较如表4所示. 由表4可知,IDEBBO算法对8个标准函数的测试结果包括最优值、最差值、均值、标准差均比较明显的优于IBBO等其它算法. 表4 测试函数结果对比 Table 4 Result comparison of test functions 函数最优值最差值均值标准差FOADEBBOIBBOIDEBBOFOADEBBOIBBOIDEBBOFOADEBBOIBBOIDEBBOFOADEBBOIBBOIDEBBOF12.8473E+002.0032E+006.0792E+001.9292E+006.2900E-022.6472E+012.2827E+012.0318E+012.0282E+012.0333E+019.6620E+008.3382E+009.1308E+007.4331E+005.1128E+005.9815E+005.4149E+003.2467E+004.8016E+005.5378E+00F22.6947E+022.3637E+002.2606E+021.5329E+025.0610E-018.4237E+046.5807E+046.2431E+045.0575E+044.4461E+045.2041E+034.0372E+033.2533E+032.9291E+032.4385E+031.3728E+041.0500E+048.2591E+037.5396E+037.7741E+03F35.5384E+005.0254E+005.0292E+007.5940E-011.2200E-018.0047E+027.0037E+026.93R8E+026.0152E+027.3135E+021.0563E+026.2950E+013.2960E+012.8885E+013.9325E+011.8708E+021.4469E+029.0917E+018.6226E+011.1865E+02F43.2954E+022.0043E+021.1758E+029.9397E+002.3713E+001.0289E+049.0034E+038.0950E+031.7537E+047.8124E+031.6438E+031.0989E+032.6122E+021.6212E+024.8448E+012.7098E+032.2734E+038.2594E+021.3675E+035.6025E+02F53.1656E+012.9489E+013.8788E+012.853RE+011.3253E+015.1347E+025.0910E+025.0919E+025.1076E+024.9547E+029.1816E+018.2549E+017.8055E+017.89903+017.2417E+019.5803E+01P8.8272E+017.7635E+018.4454E+011.0203E+02F63.7400E-022.4300E-022.9000E-026.2000E-032.5000E-034.1880E-013.9480E-014.0770E-012.1950E-013.1590E-011.4140E-017.2400E-026.0800E-025.4100E-027.9000E-031.0580E-015.6700E-023.9300E-024.8000E-023.4900E-02F74.5320E-013.9800E-013.9800E-013.9790E-013.8760E-013.0373E+002.8434E+006.4820E-012.0417E+002.9884E+005.2830E-014.5790E-014.5370E-014.2660E-014.2810E-013.1430E-012.9590E-015.9600E-022.0010E-012.5970E-01F8-8.3048E+01-8.3613E+01-8.3561E+01-8.3790E+01-1.0455E+02-6.5037E+01-8.0047E+01-6.7020E+01-8.0297E+01-8.0655E+01-8.2456E+01-8.3204E+01-8.3335E+01-8.3620E+01-8.6598E+011.9026E+016.8435E+001.6569E+012.7817E+007.2788E+01 4.3.1 函数收敛曲线对比 由于篇幅限制,以下仅列出具代表性的函数F1、F5、F6、F7、F8分别被三种算法优化所得的迭代曲线对比如图2至图6所示. 图2 F1函数收敛对比曲线图Fig.2 Convergence curve of F1 函数F1和F3均为搜索区间里分布有大量局部极值的高维多峰函数,如图2所示,IDEBBO算法寻优精度均较为明显地优于IBBO等其他四种算法.函数F2是寻优难度较小的单峰函数,改进后的IDEBBO在迭代接近50代时找到优于其他算法的最优值. 图3 F5函数收敛对比曲线图Fig.3 Convergence curve of F5 函数F4由于本身是一个病态二次函数,其仿真图形中的全局最优值位置在一个类似狭长的甬道,容易使算法在寻优过程中陷入局部最优,IDEBBO算法会跳出停s滞过程的局部最优且优化精度较另外四者高.如图3所示,函数F5是一种具有较多局部峰值的多峰函数,可用于验证算法跳出局部最优的能力,IDEBBO算法设计时融合了全局和局部的搜索能力,增强的种群多样性有助于算法跳出迭代初期的局部最优,进而搜索到全局最优.如图4、图5所示,函数F6、F7由于维度较低,五种算法均能搜索到最优值,对F6表现出的寻优性FOA较低.另外四个较优.对F7表现出的寻优性大致相似,IDEBBO稍优于另外四个. 图4 F6函数收敛对比曲线图Fig.4 Convergence curve of F6 图5 F7函数收敛对比曲线图Fig.5 Convergence curve of F7 如图6所示,函数F8的收敛曲线表明了IDEBBO优化所得最优值最接近最优解. 4.3.2 算法效率对比 如图7所示为三种算法效率对比,结合表4及收敛曲线图可知,由于IDEBBO算法中加入基于Fibonacci数列的迭代思想和基于差分思想改进的变异算子,一定程度上影响算法效率,但IDEBBO算法的寻优精度整体上均高于其它四种算法,符合算法改进的宗旨,即保证算法效率不被严重影响的前提下,提高算法的寻优精度. 图6 F8函数收敛对比曲线图Fig.6 Convergence curve of F8 图7 算法效率对比Fig.7 Efficiency comparison 针对基本BBO算法在求解高维复杂问题时求解精度低,收敛速度慢且易陷入局部极值等问题,本文提出了一种改进的IDEBBO算法,首先基于Fibonacci数列的迭代思想消除种群内部的重复性来提高种群精度,设计一种改进的IBBO算法,然后在此基础上引入全局搜索能力较强的差分进化算法中的差分进化思想来改进IDBBO算法中的变异算子,产生新型差分进化变异算子,给出改进的IDEDBBO算法.最后通过对8个经典测试函数的仿真测试对比,实验结果表明了IDEBBO算法在对函数进行优化时跳出局部极值的寻优性能、收敛能力等方面均显著优于BBO等其它四种算法,可用于解决实际工程应用中多目标或非线性等一系列复杂函数的优化问题.
Table 1 Pseudocode for the IBBO algorithm
3.2 IDEBBO算法设计
Table 2 Differential mutation operation of IDEBBO
4 实验与仿真
4.1 实验参数设置
4.2 标准测试函数
Table 3 Standard test function
4.3 实验结果分析

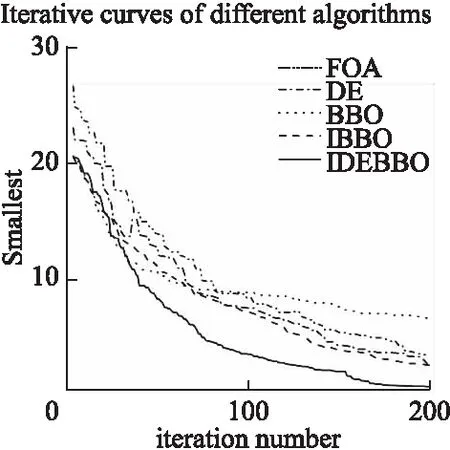
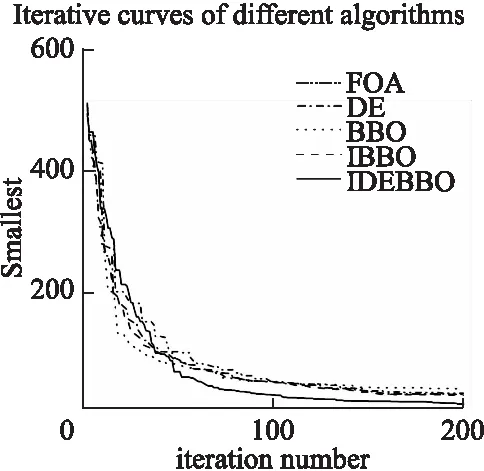
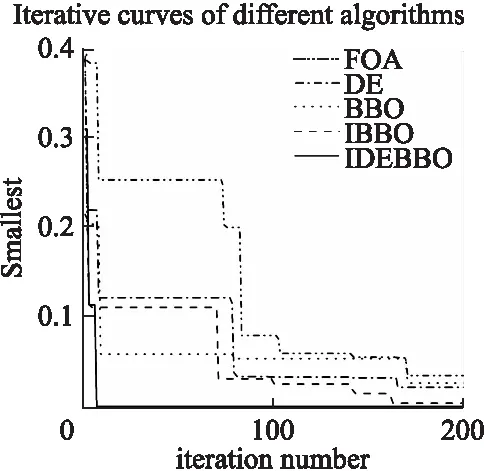

5 结束语
