基于关键路径的工作流瓶颈挖掘与优化
2019-07-09杜明达林荣恒
杜明达,林荣恒,邹 华
(北京邮电大学 网络与交换国家重点实验室,北京 100876)
1 引 言
当今世界,信息化已经成为经济社会发展的总体趋势,越来越多的工作通过计算机和网络的参与得以展开和完成,我们将工作流程中的逻辑和规则抽象化并建模成为工作流,文档、信息和任务等以数据的形式,按照预先设定的规则在工作流中的不同节点之间传递,驱动工作流的执行[1].根据BPMN(Business Process Model and Notation)1的定义,一个工作流是由若干事件(event)、活动(activity)、网关(gateway)和连接对象(connecting objects)等组成的.事件主要包括开始事件和结束事件,代表一个流程的开始和结束,活动代表需要完成的任务,活动之间通过连接对象进行连接.在比较复杂的工作流中,往往存在分支,即一个事件结束后可能有多个备选事件,根据预先设定的条件触发下一个事件,分支的分流与合并用网关表示.
在实际的生产生活中,当一个工作流经过部署并执行一段时间后,我们往往更关心流程实际执行的效率及可能存在的瓶颈.如果能够通过对工作流的执行日志和历史数据等的挖掘找到流程执行的瓶颈,并对其进行有针对性的优化,对于提高该工作流的执行效率和整个生产生活的效率都有积极的意义.考虑到工作流是从开始事件为起点,沿着某条路径依次完成路径上的任务,最终以结束事件为终点,同时我们可以从流程的执行日志和历史数据中挖掘出工作流中每一个任务的执行时间,为了实现对工作流的执行瓶颈挖掘和定位,本文将给出一种将工作流的流程图转化为带权值的有向无环图,并计算该有向无环图的关键路径的方法,并针对瓶颈提出相应的解决方案.
本文的章节安排如下:第2章将介绍在工作流程分析与优化上其他人的相关工作,第3章给出对本文工作流瓶颈的形式化定义和问题建模,第4章提出检测工作流瓶颈的模型及解决算法,第5章以一个实际的例子进行实验对模型及算法进行可行性验证,第6章是结论.
2 相关工作
工作流程可以用三种方式定义模型:第一种是图像表示法,采用流程图的方式进行工作流的表示,从而可以快速地构建工作流程并直观进行展示;第二种是数学表示法[2],采用形式化语义对工作流程进行严格准确的概念定义,这种方式的出现为使用数学分析工作流程、提取知识和推理提供了可能;第三种是业务流程语言[3],它结合了前两种方式,以明确的语义来定义更加复杂的形式化模型,并用图形化的方式表示其结构,这种建模方式迅速成为主流并出现了很多规范,业务流程建模语言(BPML)[注]2 OASIS, Business process execution language (WS-BPEL 2.0), wsbpel-v2.0-OS, OASIS, http://docs.oasis-open.org/wsbpel/2.0/wsbpel-v2.0.html,2011.就是其中的代表.工作流程的优化的目标和方向,主要分为几个方面:1)缩短交付时间和成本,提高产品质量,增强用户满意度[4];2)降低成本和流程时间[5];3)提高设计的“最优性”,由于流程的质量由许多常常互相冲突的标准来定义,故需要达到这些标准的整体最优[6].
为了实现流程的优化,根据工作流程定义的方式及工作流程所在的场景,不同的人给出了不同的解决方案.文献[7]提出了采用图元(metagraph)的数据接口来表示工作流;从而为科学地分析工作流、更有效地设计组织流程提供解决方法;文献[8]提出使用活动图对工作流进行建模,进而转化为Petri图,使用Petri网分析工作流模型;文献[9]提出一种将带有时间信息的有向网络图所表示的工作流模型抓华为时序约束工作流网络的模型映射方法;文献[10]提出一个对工作流循环范式进行规范分析的框架.近年来,人们越来越关注对工作流执行产生的事件日志的挖掘,文献[11]采用ProM框架实现对流程的决策挖掘,检测影响流程路由选择的数据依赖;文献[12]给出了将ProM框架应用于流程日志挖掘应用于道路及水利基础设施建设及维护的例子;文献[13,14]分别在医疗保健和广告市场中对工作流程的日志进行挖掘和分析.
在流程分析和流程优化技术上,文献[15]基于工作流可以视为图形的事实,将图形内核应用于工作流的分析工作中,如工作流发现、工作流推荐、工作流模式提取等.文献[16]实现了一个基于电子表格的业务流程分析工具;文献[17]提出一个同时优化流程结构和流程执行策略的数学规划模型.George Tsakalidis团队提出了以演化计算技术为基础的流程优化框架[18],后来在框架中引入两个计算单元[19],分别用于补货流程设计及计算与评估流程属性,同时引入算法检查每个候选解决方案的可行性.
3 问题定义
本章将给出关于流程瓶颈的定义,并对解决问题进行定义和建模.
3.1 流程瓶颈定义
对于流程的执行瓶颈,我们定义如下:流程中每个活动都有对应的执行时间,每个流程也对应一个总的执行时间,如果存在某个活动,当该活动的执行时间缩短或延长时,流程的总执行时间也相应缩短或延长,我们则称该活动为流程的执行瓶颈.对于存在多条执行分支及多个任务活动的流程,可以具有多个执行瓶颈.我们将多个在逻辑上具有连续性的执行瓶颈构成的执行路径称为流程的关键路径.显然对于关键路径上的活动,都是我们可以考虑优化的目标活动.
以图1所示的流程图为例,在流程中一共存在三条执行路径:
P1:estart→e1→g1→e2→e3→g2→e4→g3→g4→e8→eend
P2:estart→e1→g1→e2→e3→g2→e5→g3→g4→e8→eend
P3:estart→e1→g1→e6→e7→g4→e8→eend
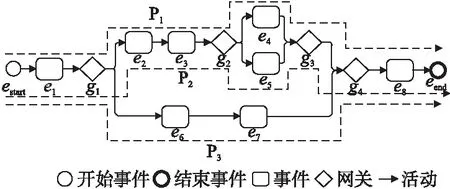
图1 一个简单的流程图Fig.1 A simple flow chart
对于三条执行路径,直观上会认为P1,P2的执行时间要高于P3所需要的执行时间.然而我们需要通过计算每一条路径的平均执行时间才能得到最终的结果.当e6、e7的总执行时间过大时,可以导致P3的总执行时间要高于其他两条执行路径.
当实际生活中给定的流程更加复杂,节点更多,分支更多时,我们在设计初期往往很难把握哪些节点的存在导致了整个流程的执行时间变长.
我们可以采用反证法证明,在具有多条执行分支的流程中,总的执行时间最长的执行路径就是流程的关键路径.假设存在一条执行时间不是最长的执行路径,它也是流程的关键路径,根据前文中流程关键路径的定义,该路径上的所有活动都要满足“当该活动的执行时间缩短/延长时,流程的总执行时间也相应缩短或延长”.对于该路径上的活动,如果该活动也在执行时间最长的路径上存在,显然满足定义.对于不在执行时间最长的路径上存在的活动,当活动的执行时间变短时,该执行路径的总执行时间也将相应变短,然而流程的总执行时间与流程中最长的执行路径的执行时间相关,此时该活动并不影响最长的执行路径的执行时间,故流程的总执行时间并不会相应变短,不满足条件.因此,一个流程中执行时间最长的执行路径就是流程的关键路径.
对于流程的每一个执行实例,我们可以轻易地从流程的执行日志中计算出该实例上每一个活动的执行时间,因此,对于一个给定的流程,我们可以统计多个执行实例中每个活动的执行情况,得到一个平均的执行时间,这个时间代表了一般情况下该活动的执行时间.
故我们要解决的问题可以转化为,对于任意一个给定的具有多条执行分支的流程,我们要找到多条路径中总执行时间最长的路径,该路径就是流程的关键路径,该路径上的每一个活动都是流程的执行瓶颈,通过对这些执行瓶颈的分析和优化,我们有希望提高这些执行瓶颈的执行效率,从而提高整个流程的执行效率.
3.2 问题定义
根据上一小节中我们对流程瓶颈的定义,我们结合BPMN中对工作流程的定义,以形式化的方式对问题进行定义,以求更清晰和准备地描述问题,为下一章模型的提出和算法的设计做铺垫.
我们定义工作流程为S=(E,A,R,C).
其中E= {estart,,e1,e2,…,e|E|-2,eend}为事件集合,特别地,estart,表示开始事件,eend表示结束事件.
A= {a1,a2,…,a|A|} 为活动集合.
R= {ri:ea×eb→ai|aa,ab∈E,ai∈A} 为E集合与A集合的映射关系集合,表示了事件和活动之间的对应关系,一个活动连接了两个事件.
C= {c1,c2,…,c|A|} 为活动消耗时间的集合,每一个活动ai对应一个ci.在工作流中,活动ai所连接的两个事件的起始时间的差值,即为该活动的耗时ci.
根据流程瓶颈定义,对于一个工作流程S,我们需要计算找到A的一个最小子集AC,满足:
1)连通性:estart经过所有Ac后能到达eend;
2)唯一性:去掉AC中的任意元素ai, 1)无法成立;
3)在满足连通性和唯一性的条件下,AC的总耗时为最大.
我们希望可以找到这样的子集AC,并通过优化AC,使得AC的总耗时变小.
4 解决方案
在上一章中我们得到了流程瓶颈的定义,在本章中我们提出将工作流的流程图转化为带权值的有向无环图,并计算该有向无环图的关键路径的方法,涉及到对流程图的模型定义,对关键路径的计算的算法.大致的流程如图2 所示.
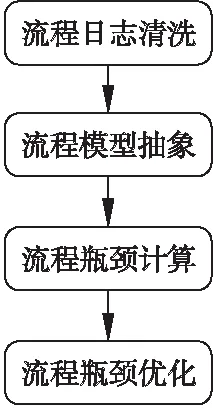
图2 基于关键路径的工作流瓶颈挖掘与优化的总体流程Fig.2 Overall process of workflow bottleneck mining and optimization based on critical path
其中流程日志清洗部分,将目标流程的日志从流程日志中分离出来,剔除异常数据,并计算每一个流程实例中每个活动的执行时间,进而算出该活动的平均执行时间,代表流程中该任务的执行时间.流程模型抽象部分,将采用带权值的有向无环图对流程进行建模.流程瓶颈计算部分,提出基于关键路径的流程瓶颈挖掘方法,对流程瓶颈进行计算.流程瓶颈优化部分,根据流程瓶颈计算结果,结合业务流程的具体场景,给出可能的优化方案.
4.1 模型定义
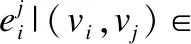
进一步的,我们将网关从流程图中去掉,则图1所示的流程图最终对应的有向无环图如图3所示.
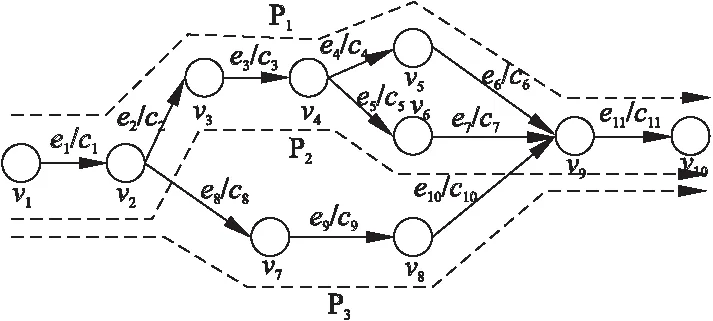
图3 图1流程图对应的有向无环图Fig.3 Directed acyclic graph of flow chart in Fig.1
问题转化为求该带权值的有向无环图G的关键路径CP(Critical Path).
关键路径CP是G中从起点到终点的最长路径,由于在流程中有些活动可以并行执行,故CP的权值之和代表了执行完该工作流程的最长时间,路径上的每条边所代表的活动即为工作流程的执行瓶颈,缩短CP上任一边代表的活动的执行时间,都可以缩短整个工作流程的总执行时间,提高工作流程的执行效率.
在图1 所示的流程图中,我们通过计算可以得到:
P1的执行时间为C1=c1+c2+c3+c4+c6+c11
P2的执行时间为C2=c1+c2+c3+c5+c7+c11
P3的执行时间为C3=c1+c8+c9+c10+c11
故最长路径为maximum(C1,C2,C3).
4.2 基于关键路径的流程瓶颈挖掘方法
本节将具体描述基于关键路径的流程瓶颈挖掘方法.我们将流程图形式化描述得到带权值的有向无环图G后,基于计算关键路径的方法对该有向无环图进行计算,从而得到流程的瓶颈.该方法包括了以下两个过程.
过程1.通过拓扑排序找出图中所有节点的合法执行顺序.
输入:有向无环图G的V集合、E集合
输出:图G各节点的拓扑排序序列topologicalSort数组
1 初始化一个数组inDegree[]用于存储每个节点的入度,初始值均为0
2 对于E中的每一条边e={vi,vj}:
3 更新inDegree[j]的值为inDegree[j] + 1
4 初始化一个空的数组topologicalSort[]表示拓扑排序的结果
5 当节点集合V中还有节点未加入数组topologicalSort中时:
6 遍历集合V中未加入数组topologicalSort且入度为0的节点v:
7 将v加入数组topoligicalSort末尾
8 遍历集合E中的每一条e={vj,vi}:
9 更新inDegree[j]的值为inDegree[j] - 1
10 返回结果数组topologicalSort
过程2.根据拓扑排序结果计算每个节点的最早开始时间和最晚开始时间,最早开始时间与最晚开始时间相等的节点即为关键路径上的节点.
输入:有向无环图G的V集合、E集合、C集合,topologicalSort数组
输出:关键路径的节点集合CP
1 定义数组EST[]表示节点的最早开始时间
2 定义数组LST[]表示节点的最晚开始时间
3 按顺序遍历topologicalSort数组中的每一个节点vi:
4 若是第一个节点,更新EST[i]的值为0
5 若不是第一个节点,遍历集合E中所有以vi为目标节点的边ea={vj,vi}:
6 计算(C[a] +EST[j])的值
7 将所有(C[a] +EST[j])的值计算完毕后取最大值即为EST[i]的值
8 按逆序遍历topologicalSort数组中的每一个节点vi:
9 若是最后一个节点,更新LST[i]的值为EST[i]
10 若不是最后一个节点,遍历集合E中所有以vi为开始节点的边ea={vi,vj}
11 计算(LST[j] -C[a])的值
12 将所有(LST[j] -C[a])的值计算完毕后取最小值即为LST[i]的值
13 初始化一个空的集合CP表示关键路径上的节点
14 遍历集合V中的每一个节点vi:
15 如果EST[i]与LST[i]相等,将vi加入集合CP中
16 返回结果集合CP
经过过程1与过程2的计算,最终我们得到了有向无环图G中最早开始时间与最晚开始时间的相等的节点的集合,该集合所能组成的路径即为原流程的流程瓶颈.
5 实验与结果分析
本章将分两部分进行,第一部分是对基于关键路径的流程瓶颈挖掘方法进行正确性的验证,第二部分我们将该方法应用与一个具体的流程中,通过对流程数据的挖掘和分析找出流程瓶颈并进行优化,验证方法的可行性.
5.1 方法的正确性验证
如图4所示,我们选取了一个具有100个节点的有向无环图进行基于关键路径的流程瓶颈挖掘方法的验证,其中实心的节点构成的路径为预期的流程的关键路径,通过计算我们得到的实际关键路径为:
1→2→3→4→6→7→14→15→16→17→18→23→24→26→28→27→29→30→31→32→37→36→38→41→42→43→44→64→63→62→66→69→70→77→78→79→80→82→83→90→91→92→93→94→95→96→97→98→99→100.符合预期.
5.2 方法在具体流程实例中的应用
我们以某公司的物资申请流程为例,流程的起点为各科室发起物资申请,根据物资的内容分为大宗物资和小件物资,大宗物资需要制定采购计划并提交院务办审核,审核通过后提交财务审核,之后由采购科进行采购及后续的核对和验收,之后入库并进行物资发放.若是小件物资的申请,则直接查询库存,库存充足则直接发放物资,库存不足则发起采购并提交财务科审核,之后的流程与大宗物资采购的流程一致.
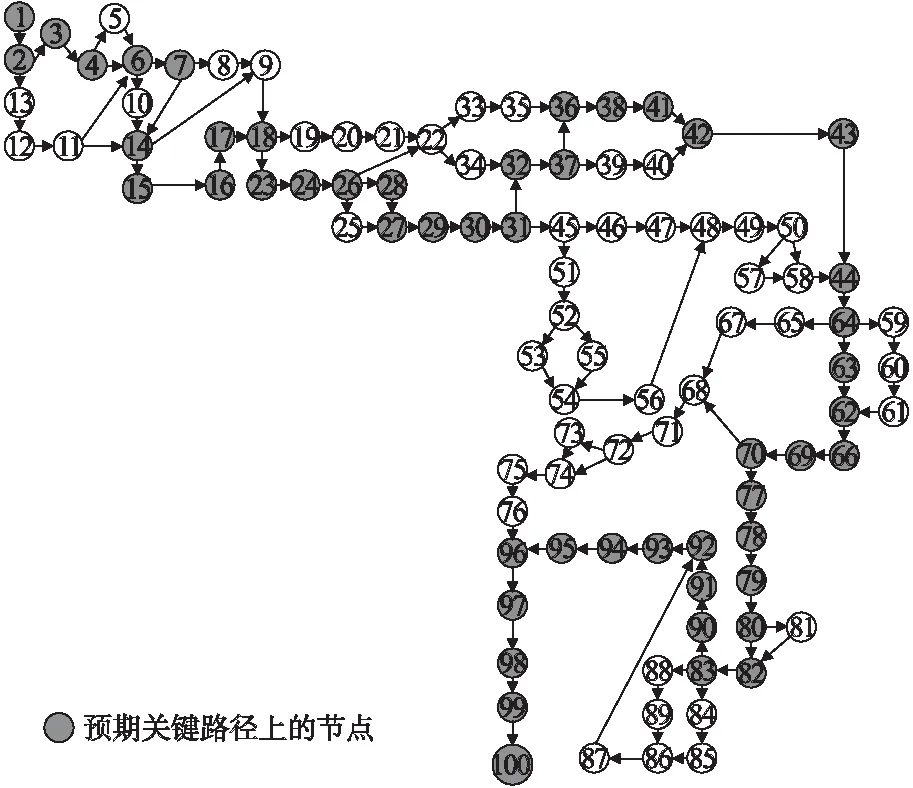
图4 一个具有100个节点的有向无环图Fig.4 A directed acyclic graph with 100 nodes
该物资采购的流程及对应的有向无环图如图5,图6所示.
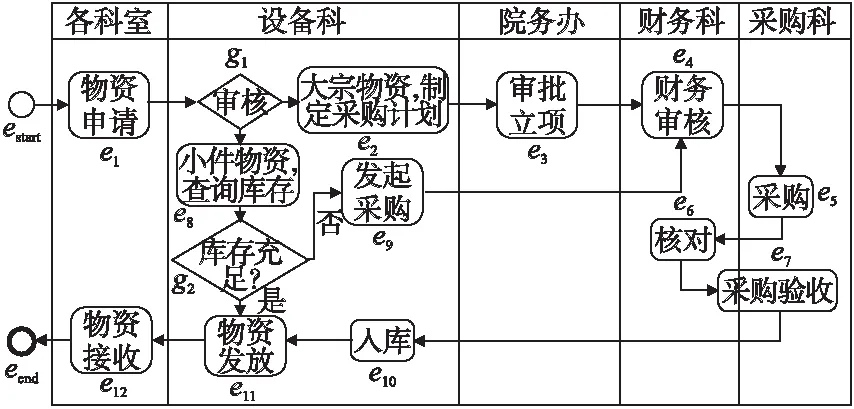
图5 物资采购流程图Fig.5 A material procurement flow chart
我们选取该流程实际执行之后得到的日志,统计后得到如图7所示的数据.
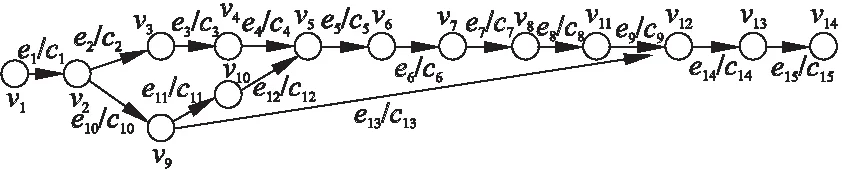
图6 物资采购流程的有向无环图Fig.6 Directed acyclic graph of material procurement flow chart
经过计算后得到的关键路径为:
v1→v2→v3→v4→v5→v6→v7→v8→v11→v12→v13→v14
该流程的总耗时约为27.30小时.
我们将关键路径上的各个节点与流程图对应之后可发现,造成流程执行瓶颈的路径是大宗物资的采购流程.进一步分析各个节点的执行时间可以发现,大部分大宗物资在“采购”任务上的执行时间均高于执行时间,而在其后的“财务科进行核对”及“采购科进行采购验收”也花费了较多的时间.我们考虑到在从“审批立项”之后财务科进行“财务审核”开始到采购科“采购验收”的子流程,各个任务之间均存在较强的关联度.在对采购项目进行财务审核需要对各采购物资的采购细节进行审核,在采购结束后进行核对时还说需要针对采购细节进行核对,最终采购科进行采购验收时仍旧需要核对各采购细节.由于在“采购”任务上花费了大量的时间,我们可以在“财务审核”之后添加一个与“采购”并行执行的任务—“制定核验标准”,根据之前财务审核中对各种采购细节的审核,由财务科制定与本次采购相关的“核验标准”,之后的核对任务急采购验收任务可以根据该核验标准进行核对和验收,从而提高流程在“核对”任务和“采购验收”任务上的执行效率.
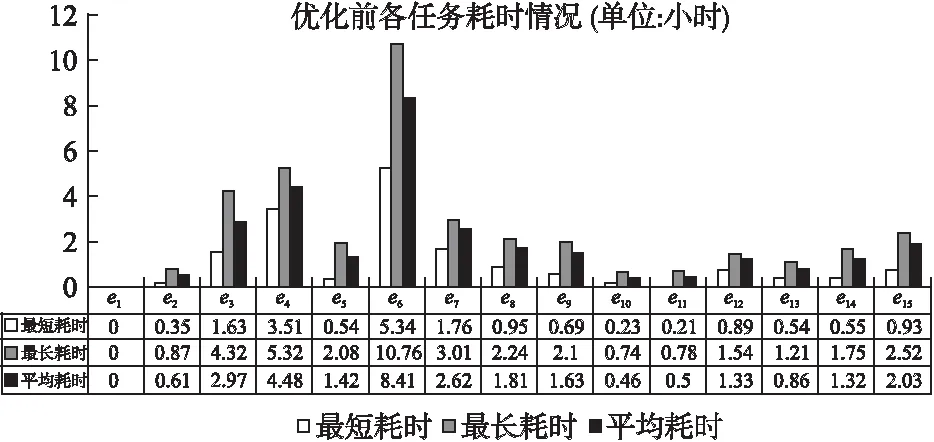
图7 物资采购流程各任务耗时情况Fig.7 Time cost of tasks in material procurement flow chart
经过优化后的流程如图8所示.
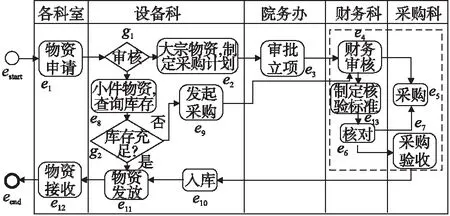
图8 优化后的物资采购流程图Fig.8 Material procurement flow chart after optimization
如之前的分析所示,在“财务审核”任务执行之后,分成了两条并行的分支,在采购科进行采购的过程中,财务科执行“制定核验标准”,之后这两条分支汇聚.
优化后的流程对应的有向无环图如图9所示.
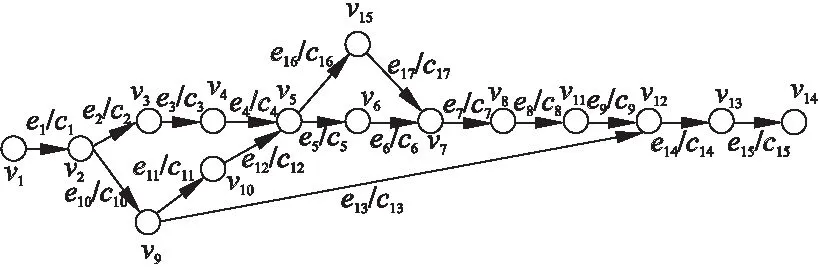
图9 优化后的物资采购流程的有向无环图Fig.9 Directed acyclic graph after optimization
我们选取改进后的流程执行一段时间后得到的日志,统计计算后得到如图10所示的数据.
经过计算后得到的关键路径为:
v1→v2→v3→v4→v5→v6→v7→v8→v11→v12→v13→v14
该流程的总耗时约为24.62小时.
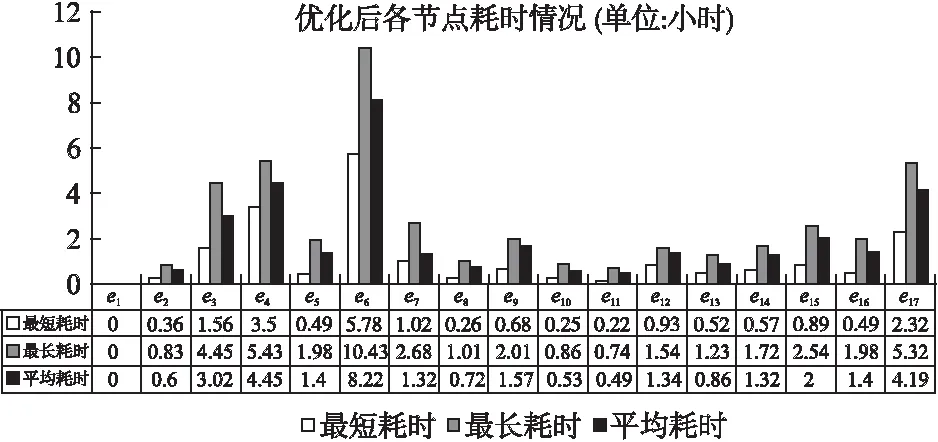
图10 优化后物资采购流程各任务耗时情况Fig.10 Time cost of tasks after optimization
5.3 实验结果分析
与优化前的流程相比,我们可以看到,优化后的流程虽然关键路径不变,但是流程总体的总耗时较优化前有所缩短.
我们将流程优化前后各个任务的平均耗时数据进行对比,得到图11.
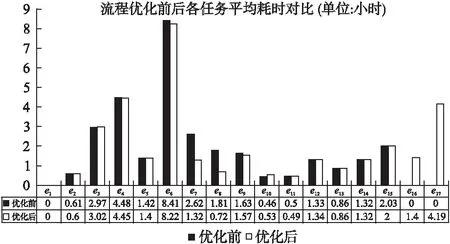
图11 物资采购流程优化前后各任务瓶颈耗时对比Fig.11 Contrast of time cost before and after optimization
可以看到,优化后,关键路径不变,关键路径上e7,e8的耗时明显下降,即“核对->采购验收->入库”的效率明显提高,其中“核对->采购验收”的平均耗时从2.62小时降到1.32小时,效率提高49.6%,“采购验收->入库”的平均耗时从1.81小时降到了0.72小时,效率提高了60.2%;整个流程增加了e16,e17两个任务,由于不在关键路径上,并不会对流程的整体执行效率起决定作用.流程的总执行时间从27.30小时降到24.62小时,效率提高了9.8%.
6 结论与不足
本文提出了工作流中关于流程瓶颈的定义,并提出将工作流的流程图转化为带权值的有向无环图,通过计算该有向无环图的关键路径得到工作流的流程瓶颈的方法,同时以某公司物资采购的流程为例,进行流程瓶颈的挖掘并根据结果给出优化方案.对于拓扑复杂,具有较多的分支的工作流程,该方法可以较快较直观地计算出流程的瓶颈,因此可以应用与相似的工作流程.
然而该方法不能很好地处理带环的工作流,对于带环的工作流,该计算可能陷入某种循环中.故对于带环的工作流,我们还需要进一步的处理,例如采用等效替换等,将工作流中的环进行抽象,用一个任务进行等效替换,对于该问题的具体方案,还有待进一步研究.
