动态规划法的应用分析
2019-07-08李小莲
李小莲


摘 要: 阐述动态规划法的基本原理及其求解方法、求解步骤,分析动态规划法在生产生活中的应用,列举了用动态规划法求解多段图的最短路径问题、资源分配问题和0-1背包问题。通过对不同实例的求解,分析动态规划法的不同计算思路,从而总结出动态规划法的优点。
关键词: 动态规划; 最短路径; 资源分配; 0-1背包
中图分类号:TP301.6 文献标志码:A 文章编号:1006-8228(2019)06-53-03
Abstract: This paper describes the basic principle of dynamic programming method, the method and procedure for solving, and analyses the application of dynamic programming method in production and life. How to use the dynamic programming method to solve the problems of shortest path,resource allocation and 0-1 Knapsack are enumerated. By solving different examples, the different calculation ideas of dynamic programming method are analyses, and the advantages are summarized.
Key words: dynamic programming; shortest path; resource allocation; 0-1 Knapsack
0 引言
动态规划法是运筹学的一个重要分支,也是计算机学里的一种重要的计算方法。动态规划法将一个复杂的多阶段决策问题转换为一系列的单个阶段的问题,利用各阶段之间的关系逐个求解。动态规划法通常基于一个递推公式及一个或多个初始状态,当前子问题的解由上次子问题的解推出,它是以牺牲存储空间换取计算时间的一种计算方法。
1 基本原理
动态规划法的基本思想是将问题分解成若干互相关联的阶段,将各阶段按一定的顺序排列。构造状态转移方程分别求出每个阶段的子问题的解,然后从子问题的解中采取自顶向下或自底向上的方式推出原问题的解。解决第一阶段的问题,依赖于解决第二阶段的子问题,解决第二阶段问题又依赖于解决第三阶段的子问题,如此类推下去直到得到原问题的解为止[1]。
2 解动态规划法的基本方法
动态规划有线性的、树型的、背包类的,不同的问题类型采用的算法并不一致,但解决问题的思路都是一样的,都需要把问题分为多个阶段来处理。
2.1 解題思路
动态规划所处理的问题是一个多阶段决策问题,一般由初始状态开始,通过对中间阶段决策的选择,达到结束状态。这些决策形成了一个决策序列,同时确定了完成整个过程的一条活动路线,如图1所示[2]。
2.2 解题步骤
用动态规划法解决问题可以分为以下几个步骤。
⑴ 按照问题的时间或空间特征把问题分为若干个阶段。划分后的阶段是有序的或可排序。
⑵ 将问题发展到各个阶段时所处的各种客观情况用不同的状态表示出来,状态的选择需要满足无后效性。
⑶ 根据相邻两个阶段的状态关系来确定决策方法和状态转移方程。给出的状态方程需是一个递推式的方程,且给状态方程设置一个终止条件或边界条件[3]。
⑷ 根据状态方程计算出各阶段的最优解。
⑸ 根据计算的各阶段的最优值信息构造出原问题的最优解。
3 动态规划法的应用
动态规划法的应用比较广泛,常用的有多段图的最短路径、资源分配问题、会议安排问题、背包问题、设备更新、最长公共子序列等,下面将分析几个应用方面的问题。
3.1 多段图的最短路径问题
多段图的最短路径问题是求从源点到终点的最短路径或者最小费用的通路,设置数组元素c[][]:存储边的长度,pre[]表示最短路径上当前顶点的前驱顶点,设置对应的状态方程:f(s)=min{f(t)+c(t,s)}[4]。
如图2,A处是一电力站,现在需要从A地架电线到E地,其中途径B、C、D三地。边上的数字表示与其相连的两地间所需架设的电线的长度。求从A地到E地所需电线的长度的最小值。
采用顺序解法,从源点出发,求到达当前状态的最短路径,然后再加入下一阶段计算,直到终点。这里分为A、B、C、D、E五个阶段,详细计算如下。
3.2 资源分配问题
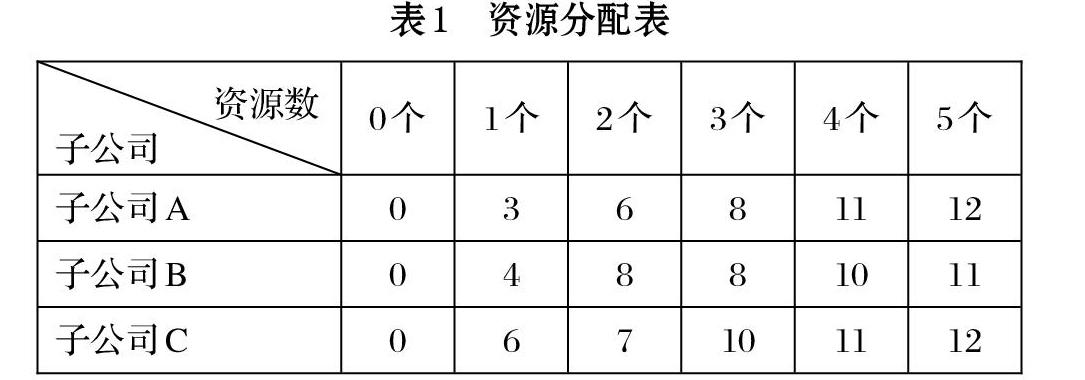
资源分配问题是对一定数目的资源进行合理分配后能够得到最大价值的问题。假设某公司共有5个新增资源,欲分配给其下属的三家子公司,各子公司得到新资源后每年的盈利情况如表1所示。表1显示的是:分配给各子公司的资源数目是多少才能使整个公司盈利最大。
采用动态规划方法,用字母i表示子公司的编号,子公司A、B、C对应编号分别为1、2、3,资源总数为n=5,子公司总数m=3。设置二位动态规划数组d,d[i][s]表示子公司i~m共分配s个资源后能获得的最大盈利,例如:d[2][4]表示子公司2~3共分配4个资源后能获得的最大盈利,即公司B和C一起共分配4个资源后得到的最大盈利。再设置二位数组p[i][s],表示求出d[i][s]对应子公司分配到的资源数。例如:p[2][4]表示求出d[2][4]时对应子公司2(子公司B)得到的资源数目。
确实好状态和状态变量,设置边界条件dp[m+1][j]=0写出对应的状态转移方程如下:
根据状态方程计算最优解,计算过程如下:
显然,d[4][*]=0(边界条件),
接下来,通过p反推各个子公司的分配资源数。p[1][5]=2,子公司A分配资源数为2,余下资源为3;p[2][3]=2,子公司B分配资源数为2,余下资源为1;p[3][1]=1,子公司C分配资源数为1,余下资源为0。最大盈利为6+8+6=20。
3.3 0-1背包问题
设背包的总重量为W,物品的重量为wi,价值为vi,且W、wi、vi都为整数,即讨论关于整数的背包问题。设置二位数组dp用来保存物品的最优解,dp[i][r]表示背包剩余容量为r时,已考虑物品1~i时背包的最大价值。xi表示物品的选取与否,按i=1,2,3,…,n的次序来确定xi的值。xi分为两种状态:
xi=0 表示物品i不装入背包中,
xi=1 表示物品i装入背包中。
0-1背包问题的状态转移方程如下[5]:
其中r=0,表示背包还能装入0个物品;i=0,表示没有任何物品可装入背包;i>0,r>0且r
请看下面实例分析:
有一个背包可容纳W=10,现有4个物品,重量记为wi={2,2,5,3},价值为vi={3,4,3,2},每个物品都不能拆分,只能选择放入或不放入,請用动态规划法求解如何选择装入背包的物品,使背包中物品总价值最大。
根据状态方程求得的dp数组以及求解过程如表2所示,其中数字右边中括号里面0表示不选取该行所对应物品,1表示选取该行所对应物品。
4 总结
动态规划,是求解问题的一种方法,它不是一种确定的算法,有多种类型的问题都可以用动态规划的思路来解,只要满足最优性原理、无后效性、有重叠子问题这三个性质,就可以用动态规划法求解。本文详细分析了动态规划方法在最短路径问题、资源分配问题、0-1背包问题等方面的应用,通过不同的应用实例,分析动态规划的解题思路,高效率地得到更完整的解信息。所有动态规划法对不同问题的解题算法也不尽相同。主要是先要确定好阶段,每个阶段的选择都很重要,先对子问题求出最优解,从而得出原问题的最优解。后续将更深入研究动态规划法在其他方面的应用。
参考文献(References):
[1] 张爱华,郭喜跃,陈前军.动态规划算法分析与研究[J].软件导刊,2014.12:68-69
[2] 赵娟,樊超.动态规划方法的应用研究[J].计算机时代,2014.2:28-30.
[3] 吕国英,李茹等.算法设计与分析(第3版)[M].清华大学出版社,2015.
[4] 李春葆.算法设计与分析(第2版)[M].清华大学出版社,2018.
[5] 刘文强,周波等.算法分析与设计课程中0-1背包问题的探讨[J].高师理科学刊,2018.6:82-85
