机械施工动荷载-采空区顶板失稳判据

李玉飞，叶义成,2，胡南燕，罗斌玉，胡盛栋，元宙昊

(1.武汉科技大学资源与环境工程学院，湖北 武汉 430081；2.湖北省工业安全工程技术研究中心，湖北 武汉 430081)

由于历史原因的影响，我国一些露天矿区形成了大量采空区[1-3]。采空区作为潜在的地质灾害之一，影响矿山的正常生产作业活动。随着露天开采的进行，护顶厚度的不断减小，当采空区上方有作业的采运、挖掘等机械施工荷载时，顶板容易发生垮落、塌陷等突发性灾害[3-5]，威胁采空区上方作业人员和采掘设备的安全。因此，准确判断机械施工荷载作用下采空区顶板失稳条件是保障露天矿安全生产的重要工作。

目前，学者大多通过数值模拟、理论分析等手段，对不同外部荷载作用下矿山空区顶板稳定性问题开展了一些研究。张建文等[2]将机械施工荷载拟为均布力，采用数值模拟分析了不同开挖高程下机械施工静荷载对采空区顶板的影响；王树仁等[3]将施工机械设备视为集中简谐动荷载，基于厚板理论研究了动荷载作用下采空区顶板应力和挠度的变化规律；邹友峰等[6]基于突变理论，建立了建筑荷载作用下采空区顶板岩梁失稳的突变模型，获得了采空区顶板岩梁保持稳定的临界条件；Nie等[7]考虑断层错动情况，通过数值模拟分析了高速公路路面下伏采空区塌陷、变形特征；李建新等[8]视列车为移动的恒定荷载，分析了列车对采空区顶板岩层应力的影响；江学良等[9]将车辆荷载简化为移动的简谐力，采用梁理论研究了车辆荷载作用下地下硐室顶板的动力响应；邓鹏宏等[10]建立了车辆荷载作用下的采空区顶板力学模型，获得了采空区顶板安全厚度表达式，并分析了车速、车质量等对顶板的影响；SINGH P K等[11]采用现场监测数据，分析了露天爆破振动对下伏空区的动力响应。

上述学者研究了不同外部荷载对空区顶板稳定性的影响，为矿山空区顶板治理提供了理论支撑。然而，研究大多视移动且非恒定的机械施工荷载为恒定的静荷载，将其简化为均布力或集中力。同时，采空区顶板岩层的失稳破坏是偏离平衡状态的非线性突变过程[6,12]，突变是采空区顶板结构失稳的一种主要形式。突变理论作为近年来发展起来的一种非线性科学理论，它注重研究系统状态发生突变时外界的条件变化。突变理论已应用到动静荷载下岩石失稳破坏[13]、充填体下采空区顶板结构失稳[14]、地下洞室稳定性评判[15]、采场顶板-矿柱稳定性研究[16]等方面，这些应用证明了该理论可以解释矿岩系统结构失稳的非线性动力学特征。目前，利用突变理论分析机械施工动荷载作用下采空区顶板非线性动力失稳的研究并不多见。另外，机械施工荷载作用下采空区顶板失稳破坏过程的应力、应变较为复杂，从能量角度可以避免研究采空区顶板失稳破坏的中间复杂受力过程[17]。因此，可以考虑从突变失稳和能量守恒角度研究机械施工动荷载-采空区顶板稳定性问题。

基于此，研究需首先分析采空区顶板破坏特征，将机械施工荷载简化为移动简谐荷载，建立机械施工动荷载-采空区顶板力学模型。然后基于突变理论，获得机械施工荷载-采空区顶板失稳判据；基于能量原理，建立临界机械施工荷载计算模型。最后对采用突变理论和能量原理建立的两种失稳判据分别进行实例验证。

1 采空区顶板破坏特征及力学模型

1.1 采空区顶板破坏特征

当采用房柱法对矿山进行开采时，其未充填的采空区剖面工程模型如图1所示[3]。图1中，当采运、挖掘等机械施工荷载驶过采空区上方时，将对下伏采空区顶板形成加载状态，并对采空区顶板产生冲击作用，使采空区顶板呈一定规律的周期性振动。一方面，当采空区顶板的自振频率与机械施工荷载的振动频率接近时，会引起共振现象，导致采空区上覆岩层内应力增大，顶板裂隙失稳扩展，进而引起顶板破坏。另一方面，当采空区顶板厚度不足，采空区上方机械施工荷载超过顶板承载极限时，将导致采空区顶板发生屈服或垮落，从而造成地表沉降或塌陷。

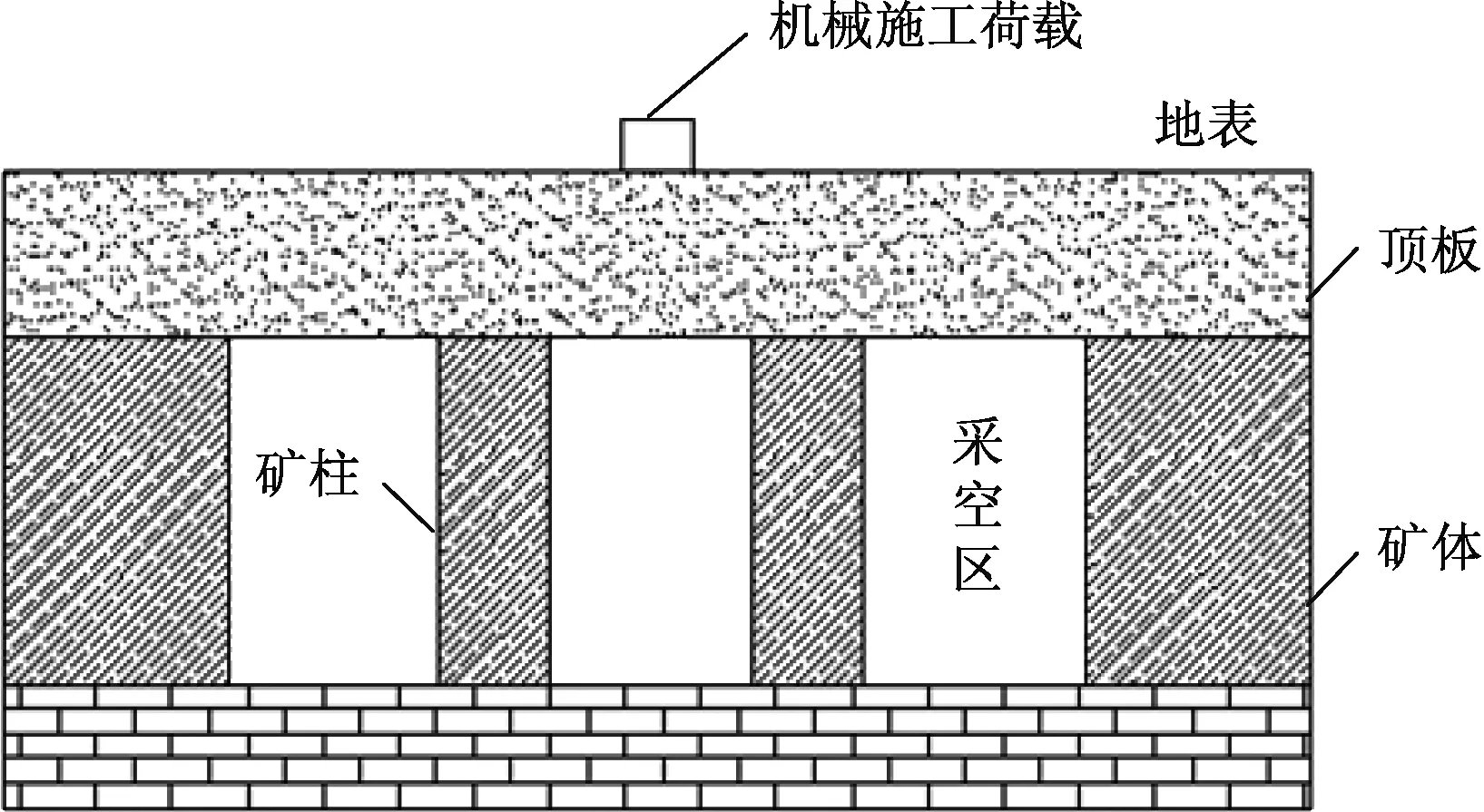
图1 工程模型Fig.1 Engineering model

1.2 采空区顶板力学模型

车辆在凹凸不平的采空区上方路面行驶时，受到激励后将发生振动，可将地面机械施工荷载视为移动简谐力[18]。为简化分析，采空区顶板岩层可看作两端受约束的水平梁，将其视为简支梁力学结构模型[9-10]，建立采空区顶板-移动简谐荷载力学模型(图2)。图中，p为机械施工初始静载；p(t)为移动简谐力。假设顶板岩梁在受力变形过程中以弹性破坏为主，且发生在一个主惯性平面内。设采空区顶板长度为L；顶板宽度为b，取单位宽度1 m；顶板厚度为h。

图2 采空区顶板-移动简谐荷载力学模型Fig.2 Mechanics model of goaf roof-moving simple harmonic force

2 机械施工动荷载-采空区顶板失稳的突变理论分析

2.1 失稳的双尖点突变模型

为反映采空区顶板结构在机械施工荷载动力作用下的非线性特性，设非平衡合力为[19]：

F=-c(x3+ax+b)(1)

式中：F——非平衡合力/N；

c、a、b——常数。

简谐荷载无论取正弦荷载形式还是余弦荷载形式，在简谐荷载作用下的顶板岩梁响应结果只相差1/4周期，并不影响研究结果。因此，假设移动简谐荷载p(x,t)为：

p(x,t)=p0cosωt(2)

式中：p0——机械施工荷载的振幅值/MPa；

ω——机械施工荷载的振动角频率/(rad·s-1)；

t——振动时间/s。

顶板岩梁在移动简谐荷载作用下作简谐振动，考虑到线性阻尼因素，根据牛顿第二定律，得到顶板岩梁在机械施工荷载作用下的振动方程：

(3)

式中：m——微元段的质量/kg；

μ——粘滞阻尼系数。

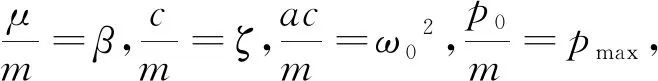
(4)

式中：β——采空区顶板结构的阻尼比；

ζ——顶板结构刚度的非线性系数；

ω0——顶板的初始自振频率/Hz；

pmax——机械施工荷载的最大振幅值/MPa。

由于机械施工荷载形式为谐波，故设式(4)方程解为：

x(t)=Hcos(ωt+φ)+H0(5)

式中：H——顶板的动力响应振幅值/m；

φ——相位差/(°)；

H0——顶板的初始振幅值/m。

将式(5)代入式(4)中，省略三次谐波项，并根据cosωt和sinωt项前的系数必为零，得到：

(6)

将式(6)两端平方相加消去φ，得到：

(7)

对式(7)作微分同胚变换，消去H2项，得到：

(B+M)3+r(B+M)+s=0(8)

其中：

(9)

由突变理论可知，式(8)为尖点突变模型的标准平衡曲面方程，其中r、s为控制变量，B+M为状态变量，可将状态变量看作由B和M两个变量组成，故式(8)可视为由两个尖点突变模型构成的双尖点突变模型(图3)。尖点突变模型作为突变理论中的突变模型之一，其临界曲面容易构造，且几何直观性强，以上表明机械施工动荷载-采空区顶板稳定性问题符合突变模型，突变理论适用于机械施工动荷载-采空区顶板非线性动力失稳研究。

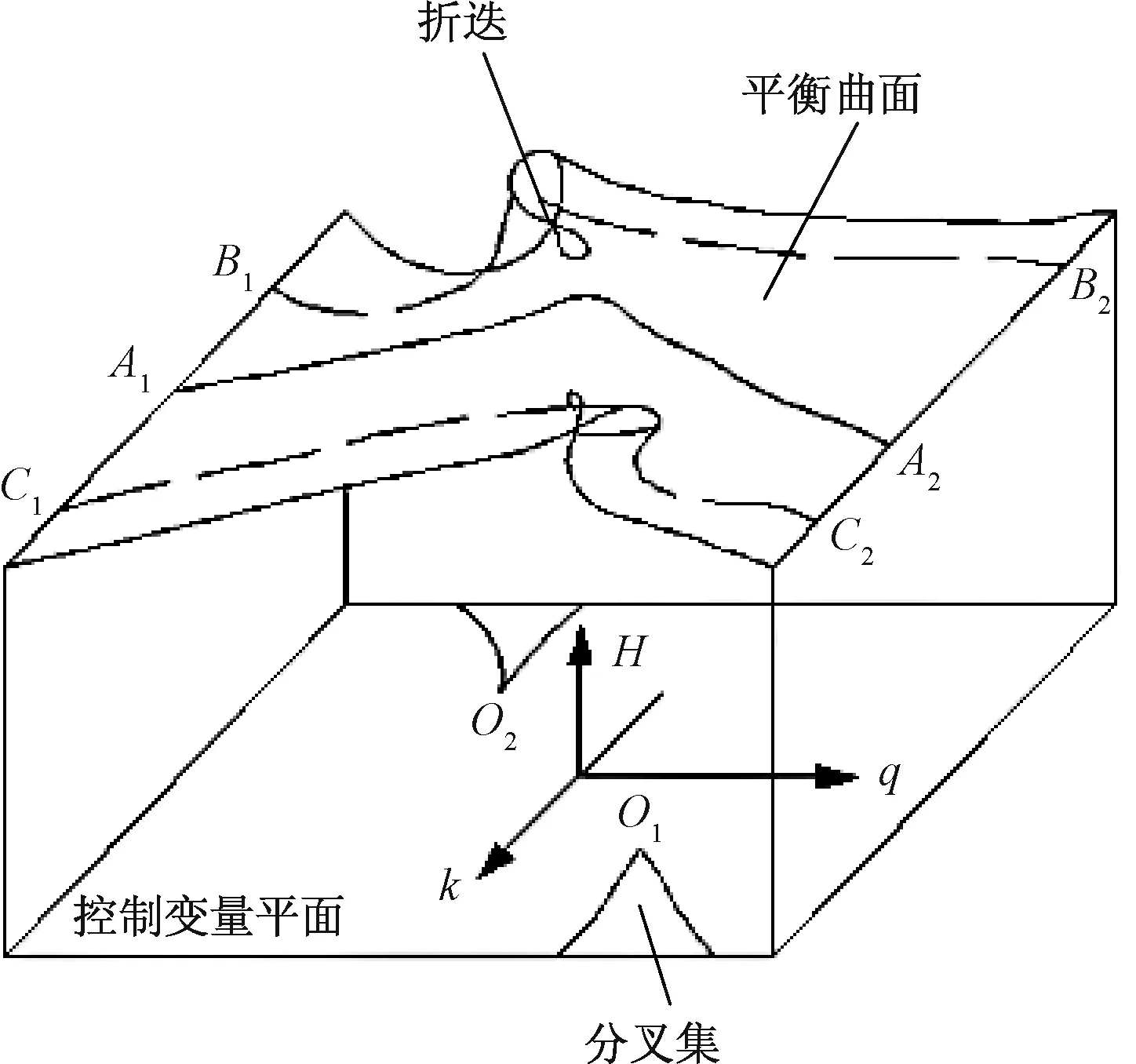
图3 双尖点突变模型Fig.3 Double cusp catastrophe model

2.2 突变失稳判据

(1)失稳的必要条件

对式(8)中B+M进行求导，得到：

3(B+M)2+r=0(10)

联立式(8)与式(10)，得到系统分叉集方程：

Δ=4r3+27s2(11)

根据突变理论知[20]，只有当r≤0时，机械施工动荷载-采空区顶板系统稳定平衡点才能跨越分叉集，此时采空区顶板产生突跃，系统将发生突变失稳。因此，r≤0是系统失稳的必要条件。即：

(12)

(2)失稳的充分条件

当稳定平衡点(r,s)位于分叉集位置时，系统处于临界状态，此时若系统受到外界的微小干扰，系统状态都将发生改变，从而使系统产生突变。因此，当Δ=0时，系统处于临界平衡稳定状态；当Δ>0时，系统处于平衡稳定状态；当Δ<0时，系统处于失稳状态。因此，Δ≤0构成系统失稳的充分条件。由式(11)得到：

3 机械施工动荷载-采空区顶板能量临界状态分析

3.1 总能量方程

由于采空区顶板长宽比一般较大，故忽略转动惯量和剪切变形对顶板岩梁的影响。根据弹性理论和能量原理，结构体总能量为该结构体的应变能和荷载势能的组合。若不计阻尼干扰力作用，由图2的力学模型知，系统总能量由集中简谐荷载做功Wp、顶板弯曲应变能Wm、顶板自重做功Wg以及顶板自重产生的势能增量WΔ组成。

顶板岩梁在集中简谐荷载作用下产生简谐振动，其挠度方程V(x,t)为：

(14)

式中：u——顶板岩梁随时间t变化的振幅/m。

取顶板岩梁中的微元段dx进行分析，考虑到集中简谐荷载对顶板产生的波动效应。则集中简谐荷载做功Wp为：

(15)

式中：v——机械施工荷载的速度/(km·h-1)。

将式(14)代入式(15)得：

(16)

顶板弯曲应变能Wm为：

(17)

式中：M(x)、K(x)——顶板岩梁弯曲后，以岩梁端点为原点的挠曲线上的弧坐标在x处横截面上的弯矩(N·m)和挠曲线曲率。

E——顶板岩体的弹性模量/GPa；

I——顶板岩梁断面的惯性矩/m4；

μ——顶板岩体的泊松比。

顶板岩梁变形曲线在x处的曲率为：

(18)

将式(18)及式(14)代入式(17)中，得到：

(19)

顶板自重做功Wg为：

(20)

式中：γ——岩体容重/(kN·m-3)。

顶板自重产生的势能增量WΔ为：

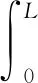
机械施工动荷载-采空区顶板系统总能量W为：

W=-Wp+Wm-Wg+WΔ(22)

将式(16)、(19)、(20)及(21)代入式(22)中，得到机械施工动荷载-采空区顶板系统总能量方程：

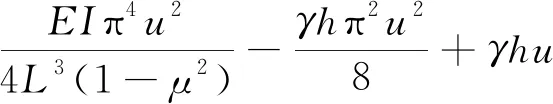
3.2 临界机械施工荷载确定

机械施工动荷载-采空区顶板的平衡条件为：

(24)

将式(16)、式(19)、式(20)及式(21)代入式(23)中，得到：

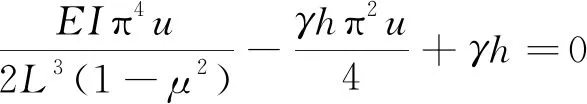
机械施工动荷载-采空区顶板的临界失稳判据为：

(26)

即：

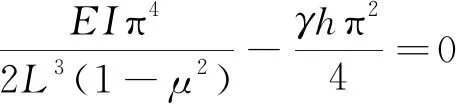
根据式(27)，可得到临界机械施工荷载pcr为：

(28)

要使采空区保持稳定，则机械施工荷载p应满足：

(29)

4 实例验证

通过查阅关于机械施工荷载作用下采空区顶板稳定性方面的文献资料，对基于突变理论的机械施工荷载-采空区顶板失稳判别式(12)及式(13)进行计算，其判别结果如表1所示，表中实测状态代表文献中理论计算、数值模拟或现场实测确定的稳定状态和失稳状态。同时，对基于能量原理的临界机械施工荷载式(29)进行计算，并将其理论值与实测值进行对比，如图4所示，表中实测值代表文献中理论计算、数值模拟或现场实测确定的数值。

其中，采空区顶板结构的阻尼比β取0.1，顶板的初始自振频率ω0为：

(30)

式中：ρ——顶板岩体的密度/(kg·m-3)；

A——顶板横截面面积/m2；

H1——顶板岩梁的跨中挠度/m，H1=L4p0/4πEI。

表1 基于突变理论的理论状态与实测状态对比

图4 基于能量原理的临界机械施工荷载理论值与实测值对比Fig.4 Comparison of theoretical and measured values of critical mechanical construction loading based on energy principle

顶板结构刚度的非线性系数ζ为：

(31)

机械施工荷载的振动角频率：

ω=2πf(32)

式中：f——机械施工荷载的振动频率/Hz。

顶板岩梁断面的惯性矩：

(33)

根据表1知，采用突变理论计算得到的理论状态与实测状态一致；通过图4知，采用能量原理计算得到的临界机械施工荷载理论值与实测值误差相对较小，最大误差为13.73%，最小误差为7.59%。平均误差为11.01%。以上应用说明了基于突变理论和能量原理建立的两种失稳判据适用于机械施工动荷载-采空区顶板稳定性分析，因此采用突变理论和能量原理研究机械施工动荷载-采空区顶板稳定性是可行的，为该类工程提供了一定的理论价值和工程指导。

5 结论

(1)将机械施工荷载简化为移动简谐力，采用力学分析建立了机械施工动荷载-采空区顶板力学模型，针对机械施工荷载作用下采空区顶板失稳破坏具有突发性及受力过程复杂的特点，研究从突变和能量角度分别建立了失稳判据，为解决机械施工动荷载-采空区顶板稳定性问题提供了一种新的定量研究思路。

(2)基于动力学理论，形成了机械施工动荷载-采空区顶板系统的双尖点突变模型，证明了采用突变理论分析机械施工动荷载-采空区顶板非线性动力失稳是可行的。由系统失稳的充分条件和必要条件，获得了机械施工动荷载-采空区顶板失稳判据式。

(3)基于能量原理，推导出由集中简谐荷载做功、顶板弯曲应变能、顶板自重做功以及顶板自重产生的势能增量组成的机械施工动荷载-采空区顶板总能量方程，根据系统临界失稳判据，获得了临界机械施工荷载计算模型。

(4)将基于突变理论和能量原理建立的两种失稳判据分别进行实例验证，采用突变理论计算得到的理论状态与实测状态一致，采用能量原理计算得到的临界机械施工荷载理论值与实测值较吻合，平均误差为11.01%。研究可为露天开采下车辆荷载大小控制、采场结构参数设置、采空区控制与治理等提供参考。