粒子与极板间作用力问题的分类剖析

浙江

随着新课改的推进，教育部正式公布的《2017年普通高考考试大纲》中涉及了动量定理知识。浙江省在2014年已将动量定理作为加试部分的重点考查对象。近几次选考真题中都有考查动量定理知识，分值大，区分度明显。笔者分析近年来各大、中、小型考试压轴题发现，很多粒子在磁场中运动射极板问题都与动量定理有关。笔者深入分析发现这类问题可归结为两种类型——垂直射极板与极板作用问题和倾斜射极板与极板作用问题。为了更好地解决这类问题，笔者对这类问题归类剖析求解，以飨读者。

1.粒子垂直射极板与极板作用问题

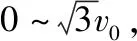
图1

(1)求离子束从小孔O射入磁场后打到x轴的区间；

(2)调整磁感应强度的大小，可使速度最大的离子恰好打在探测板右端，求此时磁感应强度大小B1；

(3)保持磁感应强度B1不变，求每秒打在探测板上的离子数N；若打在板上的离子80%被吸收，20%被反向弹回，弹回速度大小为打板前速度大小的0.6，求探测板受到的作用力大小。

【解析】离子先在电场中加速，以某一速度进入磁场中偏转，经磁场偏转后打到x轴极板上，由于离子打在极板上动量发生变化，所以离子对极板有冲力的作用。

(1)对离子在加速电场中应用动能定理有

离子打在x轴上的坐标x=2R③

联立①②③式代入数据得2a≤x≤4a

(3)离子束能打到探测板的实际位置范围2a≤x≤3a

所以每秒打在探测板上的离子数

由于离子在极板上均匀分布，离子动量随距离均匀变化，可应用平均动量思想，认为作用在板上的平均动量即为作用在板中点位置离子的动量。所以吸收的离子受到板的作用力的冲量

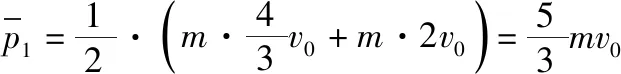
反弹离子受到板作用力大小

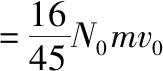
探测板受到总的作用力

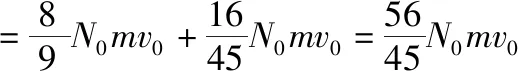
【点评】离子在磁场中偏转后与极板垂直发生作用，对极板有力的作用，求解这一作用力大小往往对离子用动量定理求解。而打在极板上的位置不同，离子的动量不同，所以题设条件中一定会告知离子在极板上均匀分布，此时可以应用平均动量的思想求解离子与极板作用动量变化量。

图2

(1)离子束射出磁场后打到y轴上的范围；

(2)若速度最小的离子在电场中运动的时间与在磁场中运动的时间相等，求电场强度的大小；

(3)探测板受到的作用力大小。

【解析】离子以不同速度进入磁场后，垂直打在极板上，与极板发生相互作用，离子动量发生变化，与极板间有力的作用，离子运动轨迹如图3所示。

图3

离子进入电场后做类平抛运动有

由于t1=t2，联立解得

(3)离子射到极板上的位置沿极板均匀分布，故可对射到极板上的离子应用平均动量思想求离子总动量。对吸收的离子应用动量定理

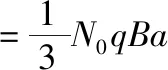
由于穿透探测板间离子能量损失64%得

故穿透探测板后离子速度为v1=0.6v

对射穿的离子应用动量定理

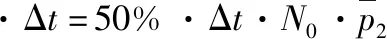
所以探测板受到离子的作用力大小

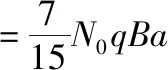
2.粒子倾斜射极板与极板作用问题

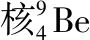
图4

(1)α粒子射出加速电场后的速度为多少？

(2)打在Q点的是什么粒子？打在Q点的粒子速度为多大？

(3)探测器上单位时间受到的撞击力为多大？

【解析】α粒子经电场加速后获得一个比较大的速度，在反应区与铍核发生核反应生成新的两种粒子，经磁场偏转后打在探测器极板上的P点和Q点。由粒子打在P点和Q点的位置易知打在P点的粒子不带电，打在Q点的粒子带正电。

(1)在加速区对α粒子应用动能定理

解得vα=4×107m/s

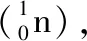
即θ=60°

碳核在磁场中做匀速圆周运动有

解得vC=1×107m/s

(3)核反应过程中根据动量守恒定律有

4m·vα=12m·vC+m·vn

解得vn=4×107m/s

在P点，对吸收的中子用动量定理

F1·Δt=50%(Δm·vn-0)·N·Δt

解得F1=3.2×10-5N，方向向下

对穿透的中子应用动量定理

F2·Δt=50%·Δm·(vn-0.5vn)·N·Δt

解得F2=1.6×10-5N，方向向下

F3·Δt=(12Δm·vC-0)·N·Δt

解得F3=1.92×10-4N，方向斜向右下方，与探测器成30°角

将F3水平和竖直方向分解后有

F3y=F3·sin30°=0.96×10-4N

探测器在y方向受到合力大小

Fy=F1+F2+F3y=1.44×10-4N

探测器x方向受到合力大小

所以探测器受到的撞击力大小

【点评】极板对粒子作用力的方向为粒子动量变化量的方向，对于粒子倾斜与极板发生作用的问题，可先根据动量定理求出极板对粒子作用力的大小和方向，再正交分解求出沿极板方向分力的大小和垂直于极板方向分力的大小，最后再进行力的合成，求出总作用力的大小和方向。