基于回归理论的烧结混合料加水参数估计

吴岳明，周纪平，吴朝霞

(1.宝钢股份上海梅山钢铁股份有限公司，江苏 南京 210039；2.东北大学秦皇岛分校 控制工程学院，河北 秦皇岛 066004)

0 引言

烧结混合料水分百分含量的稳定控制对于烧结生产十分重要，混合料水分会直接影响混合过程的制粒效果[1]。除此之外，混合料水分还会间接影响到烧结生产效率，只有将其控制在7%～7.5%左右的范围内时才会有最佳的烧结生产效率[2]。

烧结加水混合过程是一个典型的流程工业过程，对于加水过程而言，从加水到混合，再到最后的水分含量检测大约需要十分钟左右的时间。目前，大多数工厂针对该工艺的操作，仍完全或部分采用人工目测来观察出口物料的含水量，并根据各原料的下料量和总配料量凭借经验估计加水量。每次调整加水量后，还必须等待观察数分钟或数十分钟的时间，再确定是否需要进行下一步的调整。如此的大滞后调节，常会因为经验不足、操作失误或调整不及时等问题，使得混合料水分波动较大，造成烧结机生产不稳定，效率下降。也正是因为该工艺过程的大滞后性，给自动控制模型的设计带来巨大的挑战。

多年来，许多专家学者针对上述工艺过程，进行了广泛的调研和研究实验，考虑到这是一个具有典型较大纯滞后环节的流程工业过程，前馈预测控制是一个基本有效方法。1995年，金伟博士提出了以物料平衡和热量平衡为依据，建立加水模型，采用模糊集合理论建立了模糊前馈预测模型，并且进行了实际应用的实验总结[3]。2003年，孙乐等人将神经网络模型应用到混合料水分的前馈控制研究上，对其进行了有益的探索[4]。2011年，陈略峰等针对烧结混合制粒过程存在原料流量波动和时滞的问题，提出一种原料工况自适应的水分前馈串级控制方法[5]。2013年，Li Guo等通过机理分析和工艺参数的相关性，建立了RBF神经网络渗透率模型，结合渗透性综合评价模型，建立了基于渗透性的烧结混合料水分智能控制方法[6]。2016年，蔡洪岩对前馈模型中的各个物料含水量进行了参数辨识的研究，并对前馈控制模型的修正进行了仿真实验[7]。

多元线性回归分析可以根据历史的样本数据,建立多元线性回归的预测模型，从而在不需要未来样本数据的情况下，预测未来时刻多元线性回归模型中的回归参数[8]。近年来，其理论方法在许多领域都有所应用，在实际生产生活中发挥了重要作用[9-16]。回归分析在很多情况下虽然自变量和因变量之间没有严格的、确定性的函数关系，但可以设法找出最能代表它们之间关系的数学表达形式。可以认为烧结混合加水过程正是这样的一个由多种物料输入，且各物料加水参数未知的这样一个系统。考虑当各物料波动在小范围内，物料与加水量之间是一个近似线性关系，所以可以认为将多元线性回归的方法应用于加水参数估计上是可行的。

本文根据梅钢炼铁厂4号烧结机的各配料仓下料量、加水流量和水分测量值的在线测量数据，选取水分测量值为7%左右的实测数据，将多元线性回归算法应用于烧结混合过程各物料加水参数估计，之后建立回归方程，并分别利用传统烘干称重法和现场实验对所完成的加水回归模型进行验证。

1 烧结混合料加水模型

加水混合过程是烧结工艺原材料准备的过程，其工艺流程如图1所示。

图1 加水混合工艺流程
Fig.1 The process flow of adding water for mixing

从图1中可以看出，加水混合过程首先是将按比例要求配好的原料利用传送皮带运到混合机，同时根据配料量加入适量的水进行混合，混合机一边加水一边旋转，使混合料充分混合，在第一次混合完成后，再经过第二个混合机的混合制粒作用，使原料完全混合并达到所需要的含水量及粒度要求。

根据工艺流程分析可知，影响加水量大小主要因素有物料量、物料含水量、目标含水量。因此加水量的计算公式也要涉及到这些变量，其中物料含水量是整个加水模型的基础，根据物料守恒有

(1)

式中，M为混合料水分检测值，Wi为每种物料的质量，F为加水量，Ki为每种物料的含水量，i为某种物料序列数，n为全部物料的总数。

式(1)中，分母为混合料的总质量，分子为混合料中总共含水的质量。每种物料量的质量Wi可以通过每个配料仓下料时的皮带称计量得到，含水量M是二次混合机出口处的水分测量仪测量得到，加水量则是通过电磁流量计的测量显示得到。实际生产中可以将式(1)转换为

(2)

式中，FQ为前馈加水量，Mm为水分含量设定值，Wi为每种物料的质量，Ki为每种物料的含水量，i为某种物料序列数，n为全部物料的总数。

将式(2)进行整理，可得

(3)

FQ=k1W1+k2W2+…+knWn。

(4)

式中，k1，k2，…，kn为各物料加水参数，W1，W2，…，Wn为各物料质量。

式(4)就是自动预测加水控制的基础，加水量的计算是由各个物料配料量的测量值和加水参数值确定，由此需要通过多元线性回归方法估计加水参数。

2 多元线性回归法加水参数估计

2.1 数据的获取

为了对烧结混合料水分控制和混合料水分值与配料量和加水量之间的关系进行深入的研究，需要将每一种物料的配料量、混合料加水量以及水分测量值等相关的实测数据进行采集。数据已经预先从梅钢炼铁厂烧结分厂4号烧结机混合料工艺现场采集完毕，此处不再赘述采集过程。该配料车间有19个物料配料仓，每一个仓沿着传送带一线排开。物料名称以及对应的物料仓号如表1所示。

表1 物料名称和物料仓号Tab.1 Material name and bin number

用MATLAB将某时刻的实测数据的二进制文件打开，并将每一种量的数据放在相应列向量中，各料仓下料瞬时量数据如表2所示。

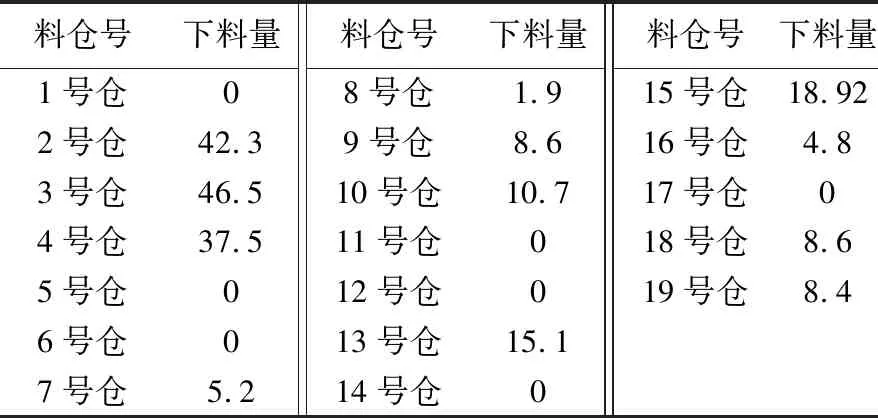
表2 各料仓下料瞬时量Tab.2 Instantaneous discharge of each bin t/h

2.2 数据的预处理

参数估计和建立回归模型需要一定量的数据，采集完的数据不能立刻作为模型的样本，因为此时的数据包括停料、状态不稳定等情况，所以要对这些数据进行预处理。数据预处理的几个步骤主要如下：

1)删除停料、开始下料的环节

在现场实际生产中，有时候因为检修、调整配料比等情况，会存在停料或状态不稳定的情况。根据烧结工艺，当加水量小于某一个值时，或者短时间内加水量出现急剧的增加或者减少，可以认为是停料，可以将停料时采集的所有的数据删除。

2)删除坏点

在删除停料等工况不稳定情况时的数据之后，还有要注意的一点是，要将不合理的点删除，这些不合理的点俗称坏点。本文采用的一种有效的去除坏点的方法是莱达因准则，这种方法可以有效地避免人为过于主观的去除坏点，好处就是尽量地减少误差，即测量的数据误差大于3σ的数据出现的概率小于0.03，σ为误差的标准差，根据概率论与数理统计的相关知识，小概率事件仅为一次实验其概率近似为零，当小概率事件发生，完全可以认为那个点就是坏点。也就是说，误差大于3σ的数据为坏点，应予以剔除。

2.3 多元线性回归加水预测模型

多元线性回归是在线性相关条件下，两个或两个以上自变量对一个因变量的数量变化关系[17]。

多元线性回归加水预测模型以式(4)为基础，加水控制模型是一个线性的模型，结合在工厂所采集的数据，在进行数据预处理后，建立多元线性回归模型：

y=β0+β1x1+…+βpxp+ε,

(5)

式中，β0，β1，…，βp是p+1个未知参数，ε是不可测的随机误差，y为被解释变量(因变量)，x为解释变量(自变量)。

模型的建立，即在确定的具体结构的基础上，通过在工厂大量采集的实测数据并对相关的数据进行预处理后，应用数理统计的方法求得β0，β1，…，βp的估计值使生产过程中可以根据自变量x1，x2，…，xm预测出因变量y的值。

现场采集大量数据，并经过删除停料、下料环节，删除坏点等预处理操作后得到一批数据，y1，y2，…，yn；x11，…，xmn。在此基础上，可以得到下列方程组：

(6)

通过求解方程，最终确定回归方程为

E(y)=β0+β1x1+…+βpxp。

(7)

在本文中β0为加水量预测回归模型的常数项，β1，β2，…，βp代表各物料的加水参数，本文共有9种物料，所以p=9，接着选取水分测量值为7%的样本数据进行回归分析，最终的加水参数估计值如表3所示。

表3 加水参数估计值Tab.3 Estimate of addition parameters

得到回归预测模型为

y=5.293+0.001x1+0.332x2+0.136x3+
0.044x4+0.127x5+0.001x6-0.032x7+
0.279x8-0.043x9。

(8)

式中，y为混合过程加水量，5.293为多元线性回归预测模型的常数项，x1，x2，…，x9分别代表混匀矿、生石灰、石灰石、白云石、内返矿、高炉返矿、粉尘、煤粉和焦炭的物料瞬时流量数值，通过各物料的瞬时流量可以计算出混合过程所需要的加水量。

3 加水参数的验证

为了分析回归模型所估计出来的加水参数的可行性，本文采用烘干称重法进行验证。首先根据已经获得的多元线性回归模型的加水参数和建立的加水回归方程，分5次按照配料工艺的物料配比要求取一定量的各种原料作为样本，然后按照回归方程计算出加水量，混合搅拌后得到混合料。接下来通过湿料称重、烘干，再继续进行干料称重等一系列步骤，最后计算出混合料的水分含量值。5个样本的取样质量数据如表4所示，加水量、烘干前后质量和混合料水分含量的计算数据如表5所示。

表4 5个样本各物料的取样质量Tab.4 The sample weight of each material for five samples g

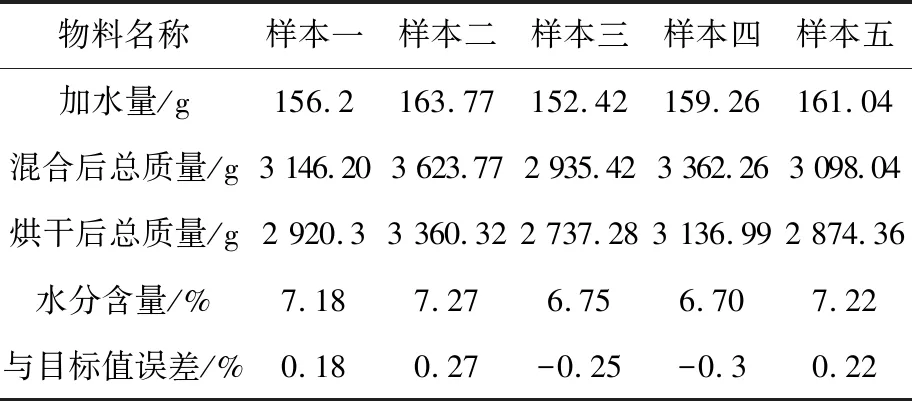
表5 5个样本加水量、烘干前后质量和混合料水分含量Tab.5 The weight of water,weight before and after drying and the moisture content of the mixture of five samples

从以上数据分析可知，5个样本按照多元线性回归模型计算的加水量进行加水并烘干验证，最终的混合料水分含量分别为7.18%、7.27%、6.75%、6.70%、7.22%，与目标值7%相比，误差分别为0.18%、0.27%、-0.25%、-0.3%和0.22%，标准偏差为0.275 4%，符合工艺指标要求。

利用烘干称重法验证多元线性回归模型后，还将预测模型放在烧结混合料加水控制系统中，并与人工手动加水进行了对比实验。人工手动控制加水时的加水量和混合料水分测量记录曲线如图2所示，采用了本文构建的回归预测模型进行自动控制加水时的记录曲线如图3所示。

图2 人工加水过程加水流量和水分含量检测值数据曲线
Fig.2 Curve of water flow and water content in manual water adding process

由图2可知，人工手动控制加水量是根据水分仪检测的数据手动开大或关小阀门，实现加水流量的改变，加水流量曲线呈阶梯型曲线，导致混合料水分测量值波动较大。由图3可知，利用回归模型进行加水流量控制时，系统可以自动根据配料量与加水系数计算出加水量并进行实时调整，使得混合料水分含量检测值波动范围小于±0.3%，且比较稳定。因此利用回归模型进行加水流量控制可以保证混合料水分波动在工艺指标要求的范围内。

图3 利用回归模型进行加水加水流量和水分含量检测值数据曲线
Fig.3 Curve of water flow rate and water content detection value by using regression models

4 结论

本文结合实际烧结生产中混合料加水工艺流程，基于物料平衡原理建立混合加水模型，并以多元线性回归理论为基础，由构建的回归模型计算出加水参数的估计值。采用烘干称重法进行了验证，结果表明依据回归模型计算出的加水量进行配料和加水，混合后得到的混合料水分含量与工艺目标值7%相比误差小于±0.3%，标准偏差小于0.3%。通过进一步的现场实验，验证了基于多元线性回归方法计算的加水参数估计值和所构建的加水量回归预测控制模型可以满足工艺控制的指标要求。所述方法具有理论参考意义和实际应用价值。