轮缘封严面网格匹配性对封严数值结果的影响

张晶辉,白 涛

(西安航空学院 飞行器学院， 西安 710077)

涡轮通道主流高温燃气会通过转子与静子之间的间隙入侵涡轮盘腔，造成涡轮盘工作环境恶劣，从而严重威胁到其安全工作。一般从压气机级间引入冷气通入涡轮盘腔以阻止主流高温燃气的入侵，同时对涡轮叶片进行冷却。封严流量越大，封严效果越好，但是封严冷气流量过大，会降低航空发动机的整机效率。涡轮封严结构设计就是要以最小的封严流量保证足够的封严效率，这就要求对封严机理有深刻的认识。

国内外学者已通过试验和数值方法对涡轮盘腔燃气入侵的机理及封严流动进行了大量研究，一般认为燃气入侵是三维非定常流动[1]。Jakoby[2]、Cao[3]和Schuepbach[4]都发现涡轮盘腔中存在低频的大涡结构。O’Mahoney[5]采用大涡模拟技术较好地捕捉到了燃气入侵的物理现象，Rabs[6]通过封严间隙内开尔文-赫姆霍兹涡的形成理论解释了非定常封严间隙涡抑制了燃气入侵的机理。

程舒娴等[7]比较了涡轮动静交界面位置对数值结果的影响，并数值研究了变工况对动叶下游压力分布和后腔封严效率的影响。杨帆等[8]通过非定常数值研究，发现封严腔体出口燃气入侵和封严出流的周向分布是由静子主导。高庆等采用SST湍流模型发现轮缘密封间隙结构会影响到间隙射流，进而影响涡轮气动性能[9]，也发现涡轮压比和转速的变化会通过影响动叶前缘压力势场分布来影响轮缘封严性能[10]。贾惟[11]非定常数值研究得到在封严流量较小时，封严腔内存在大尺度低频率的压力扰动，并向主流传播过程中强度逐渐减弱。王鸣等[12]试验发现封严腔内凸起结构可减小最小封严流量。张晶辉等数值研究了轴向封严结构内的非定常流动现象[13]，通过改变封严结构改变封严间隙内的非定常涡进而减小最小封严流量[14]。数值研究方法对封严流动计算结果会有很大影响。

已有文献通过数值计算来研究封严间隙内流动细节时，主要集中在封严机理方面，在数值方法上仅对网格进行了无关性验证，封严处网格匹配性对结果的影响鲜有报道。由于轮缘封严处为强剪切流动，流场参数梯度变化大，同时在封严间隙内存在非定常封严间隙涡，此处需要较为精细的网格划分，而工程计算中网格划分难度大且占大部分工作量，一般单独划分主流和封严间隙内的网格并设置计算域交界面，探讨封严面网格匹配性对计算结果的影响具有很大的工程应用价值。本文基于简单轴向封严结构研究轮缘封严处的网格匹配性对封严流动定常和非定常数值计算结果的影响。

1 数值计算方法

1.1 研究对象

研究对象为Aachen大学蒸汽燃气涡轮研究所1.5级涡轮盘腔试验台(图1)。两排静子各有16个叶片，转子32个叶片，封严结构如图2所示，盘腔间距比(G=s/R)为0.092 6，封严间隙比(Gc=sc/R)为0.029 6。

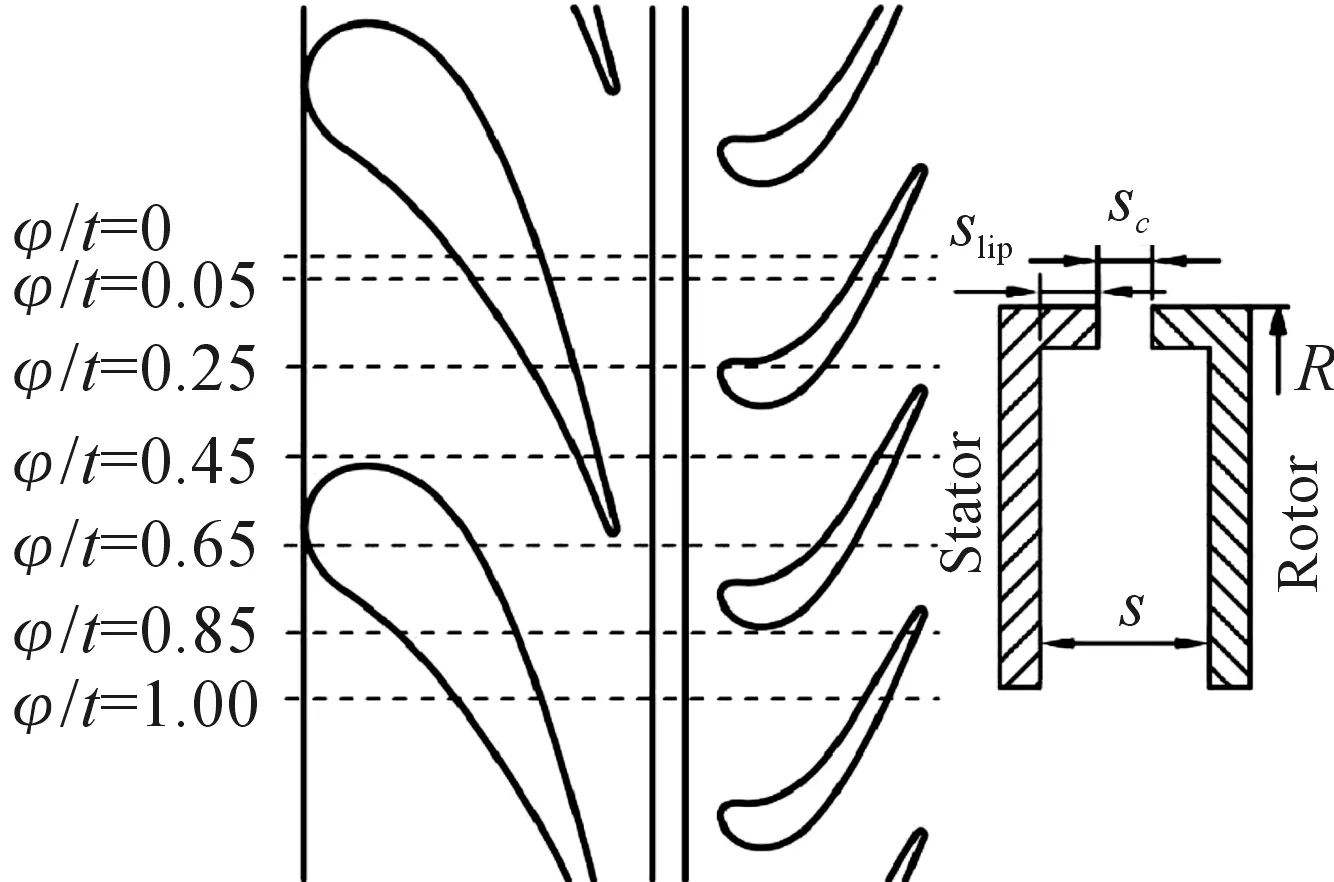
图2 轴向封严几何结构

1.2 计算模型、网格及边界条件

简化物理模型如图3所示，其进口位于导叶上游1.5倍弦长处，出口位于动叶下游1.5倍弦长处，涡轮盘腔为静子域，忽略叶顶间隙的影响。采用ANSYS-CFX 12.0软件求解三维非定常粘性雷诺平均的N-S(Navier-Stokes)方程，使用k-ωSST湍流模型，工质设置为多组分气体：主流和封严气流，但物性都为理想空气。

图3 计算域

静子域、盘腔及转子域均为结构化网格。为了研究封严处网格质量对计算结果的影响，封严面网格分别为匹配和非匹配交界面，如图4所示。匹配网格静子域和盘腔一起划分，非匹配网格分别划分，封严面处设置域交界面。网格数为247万个，周向间距最大为0.34°，主流壁面y+小于5，盘腔壁面y+小于2。采用冻结转子转静交界面进行了网格无关性验证，数值结果表明所采用的网格数量满足计算需求。

图4 网格比较

2 数值结果分析

2.1 封严面网格匹配性对定常计算结果的影响

通过封严间隙内封严气体浓度可直观地比较封严面网格匹配性对数值结果的影响，如图5、图6所示。两种网格时，燃气入侵现象都局限于封严间隙内，同一周向位置处，非匹配网格得到的封严气体浓度比匹配网格稍大，封严气体从动盘轮缘流入主流，主流燃气主要从静盘轮缘入侵封严间隙内。

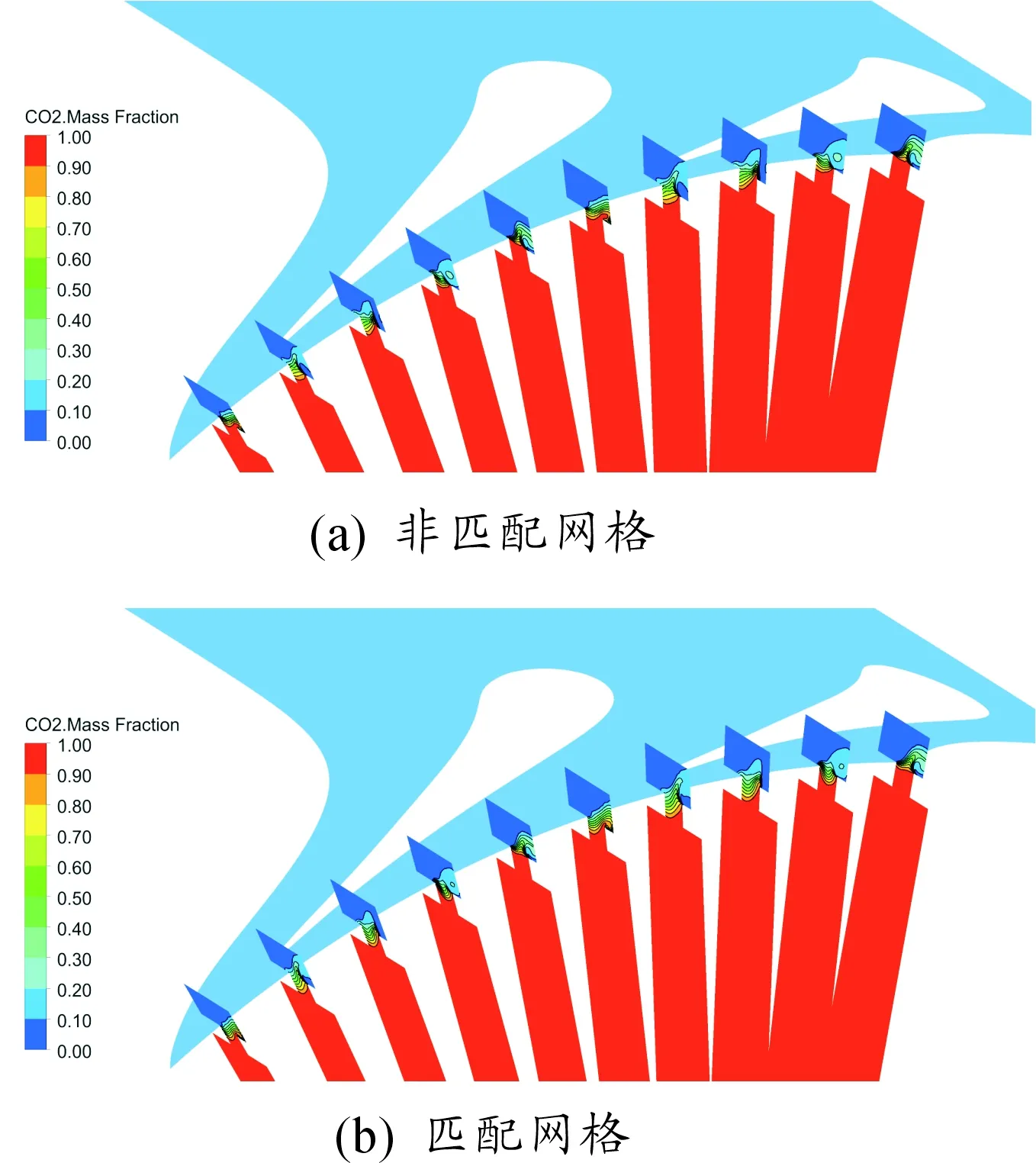
图5 封严间隙内封严气体浓度定常计算结果

图6 封严面上封严气体浓度定常计算结果

影响封严间隙内流动的因素主要是切向速度和静压分布，切向速度系数为CVtan=Vtan/(Rω)，静压系数为CPs=(Ps-Pshub)/Pshub，其中Pshub为导叶下游机匣壁面的静压分布均值。从图7、图8可以发现匹配网格时封严间隙内的切向速度较大，对比图6可以看出，这是由入侵的主流燃气高的切向速度引起，封严间隙内流场参数梯度变化大，匹配网格之间的数据传递带来的数值误差小，非匹配网格带来的数值误差大。从静压分布(图9)和径向速度分布(图10)可以看出：封严面非匹配网格引起流场参数周向变化强烈，匹配网格流场参数周向变化比较连续。

图7 封严间隙内切向速度系数定常计算结果

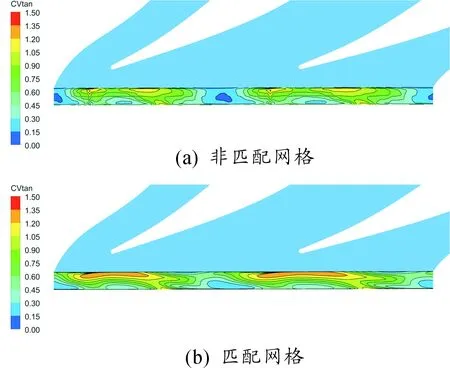
图8 封严面上切向速度系数定常计算结果

图9 封严面上静压系数定常计算结果

图10中径向速度系数CVr=Vr/Vr_ideal，其中Vr_ideal为假设封严气体在整个封严面上都以相同的径向速度流入主流。由此可见封严面网格匹配性影响封严间隙内静压、切向速度及径向速度的数值传递，对定常计算结果的影响不可忽略。

2.2 封严面网格匹配性对非定常计算结果的影响

对非定常计算结果进行时间平均的封严气体浓度如图11、图12所示，与定常结果(图5、图6)相比，非定常计算结果显示燃气已入侵到涡轮盘腔内，定常计算结果的燃气入侵仅局限在封严间隙内。封严面匹配网格计算结果显示燃气入侵更严重。

图10 封严面上径向速度系数定常计算结果

图11 封严间隙内封严气体浓度非定常时均结果

图12 封严面上封严气体浓度非定常时均结果

图13、图14为切向速度系数分布对比，封严面匹配网格时计算结果切向速度较大，对比封严气体浓度结果，发现燃气入侵区域的切向速度大于当地动盘的旋转速度。从封严面上静压(图15)和径向速度(图16)分布可以看出，封严面非匹配网格的时间平均结果显示气流参数出现较强的变化，而封严面匹配网格时气流参数的时间平均结果较为连续。由此可见封严面网格匹配性对非定常计算结果也有很大影响，封严间隙内静压、切向速度及径向速度的数值传递受到网格质量的影响。

图13 封严间隙内切向速度系数非定常时均结果

图14 封严面上切向速度系数非定常时均结果

图15 封严面上静压系数非定常时均结果

图17为盘腔内静盘壁面压力沿径向的分布，图18为盘腔内静盘壁面封严气体浓度沿径向的分布，定常结果为周向平均值，非定常结果为周向平均的时间平均值。定常计算燃气入侵局限在轮缘附近，非定常计算时主流燃气入侵到涡轮盘腔无量纲半径0.75位置处。匹配网格时非定常计算比定常计算得到的封严效率低26%。匹配网格在封严面处静子域和盘腔的网格节点是一一对应的，数值传递误差小，得到的封严效率较低。非匹配网格在封严面处静子域和盘腔网格节点不是一一对应的，主流网格较为稀疏，封严间隙内网格较为密，也考虑了壁面附面层的网格质量，因此在数值求解过程中，封严间隙内和主流的数据在封严面处通过网格插值传递。定常计算时封严面匹配网格比非匹配网格得到的封严效率低8.5%，非定常计算时封严面匹配网格比非匹配网格得到的封严效率低14%，由此可见网格匹配性对数值传递有很大影响，不可忽略。

图16 封严面上径向速度系数非定常时均结果

图17 静盘壁面压升径向分布

图18 静盘壁面封严气体浓度径向分布

3 结论

由于封严间隙内流动复杂，流场参数变化梯度大，封严面非匹配网格会带来较大的数值插值误差，定常计算时封严面匹配网格得到的封严效率比非匹配网格低8.5%，非定常计算时封严面匹配网格得到的封严效率比非匹配网格低14%，数值计算中封严面网格匹配性对计算结果的影响不可忽略，在工程计算中须对封严间隙内网格进行细致的划分，以减小插值误差。