小卫星瞬态外热流下动态传热特性分析

闾 浩，张镜洋，陶晶亮，陈 丽，张若骥

(1. 南京航空航天大学 航天学院，江苏 南京 210016；2. 上海卫星装备研究所 上海空间环境模拟与验证工程技术研究中心，上海 201102)

0 引言

当前卫星技术发展格局产生了变革。卫星的集成化和小型化技术、深空探测技术、小卫星编队组网技术成为航天技术的突出发展主题[1]。

深空探测卫星在到达遥远目标轨道或星球的飞行中，需要进行多轨道转移和对地通信的实时对准；编队和星座卫星需要进行实时而随机的姿轨调整，以满足相对位置保持的精度要求。这些应用带来卫星与日地相对关系的复杂变化，以及飞行器间的交替遮蔽影响，从而引起外热流大幅复杂变化[2-3]。更小系统热惯性和更复杂的热条件，使卫星瞬态传热特征凸显，传统稳态传热的热控设计理论难以满足卫星技术发展的新形势需求[3-4]。欧洲太空局(ESA)Magion系列卫星热控系统的研制总结中指出，稳态的热分析和试验技术难以涵盖卫星在轨复杂动态变化的热条件全状态，卫星热控系统优化和考核手段需要从瞬态的角度上进行完善[5]。中国空间技术研究院钟奇等[6-7]通过理论分析、数值仿真和专项试验，对比研究了卫星瞬态、准瞬态、稳态传热模型下的温度结果差异，认为瞬态热试验或仿真获得的动态温度均值与稳态试验或仿真值存在差异，前者接近在轨真实状态。

在此情况下，近年来瞬态热仿真和试验技术在卫星研制中被广泛应用[8]，国外的BIRD，Dawgstar等卫星，我国的试验一号、神舟伴星、天巡一号等小卫星均采用瞬态热分析和瞬态热平衡试验技术，对其热控系统设计和性能进行优化和考核[9-10]。

当前卫星热控系统的设计中多依靠稳态传热准则[11-12]，针对性的瞬态传热理论研究较为匮乏，在热分析和热试验中也缺乏普适性的瞬态传热规律指导内因分析，因此亟待开展小卫星瞬态传热规律的理论研究。

本文在建立卫星双层集总参数模型基础上，将卫星“热激励-温度响应”动态热平衡方程类比为二阶阻尼振荡系统，利用解析方法求解瞬态传热方程，利用频域传递函数分析的方法，对表征温度及热流波动量间的幅值、相位特性，随热参数变化规律进行分析。最后对解析方法求得的幅频特性和相频特性进行数值方法验证，以期为小卫星瞬态热分析、热试验提供理论分析依据。

1 模型建立

1.1 双层集总参数模型建立

将小卫星结点网络传热模型外部结构简化为壳体结点K，将进行了等温化设计的内部设备结点简化为内部结点N，建立双层集总参数模型如图1所示[12]。

图1 双层集总参数模型Fig.1 Double-layer aggregate model of microsatellite

壳体结点和内部节点瞬态热平衡方程为

(1)

Rnk(Tn4-Tk4)

(2)

从上述方程可看出，作为热控设计的目标内部结点温度Tn，随轨道外热流qs，qa，qi和内热源qn动态变化而变化。卫星在单个轨道周期内，太阳辐射热流和地球阳光反照热流随进出地球阴影区过程而发生动态变化。卫星在轨吸收热流变化如图2所示。

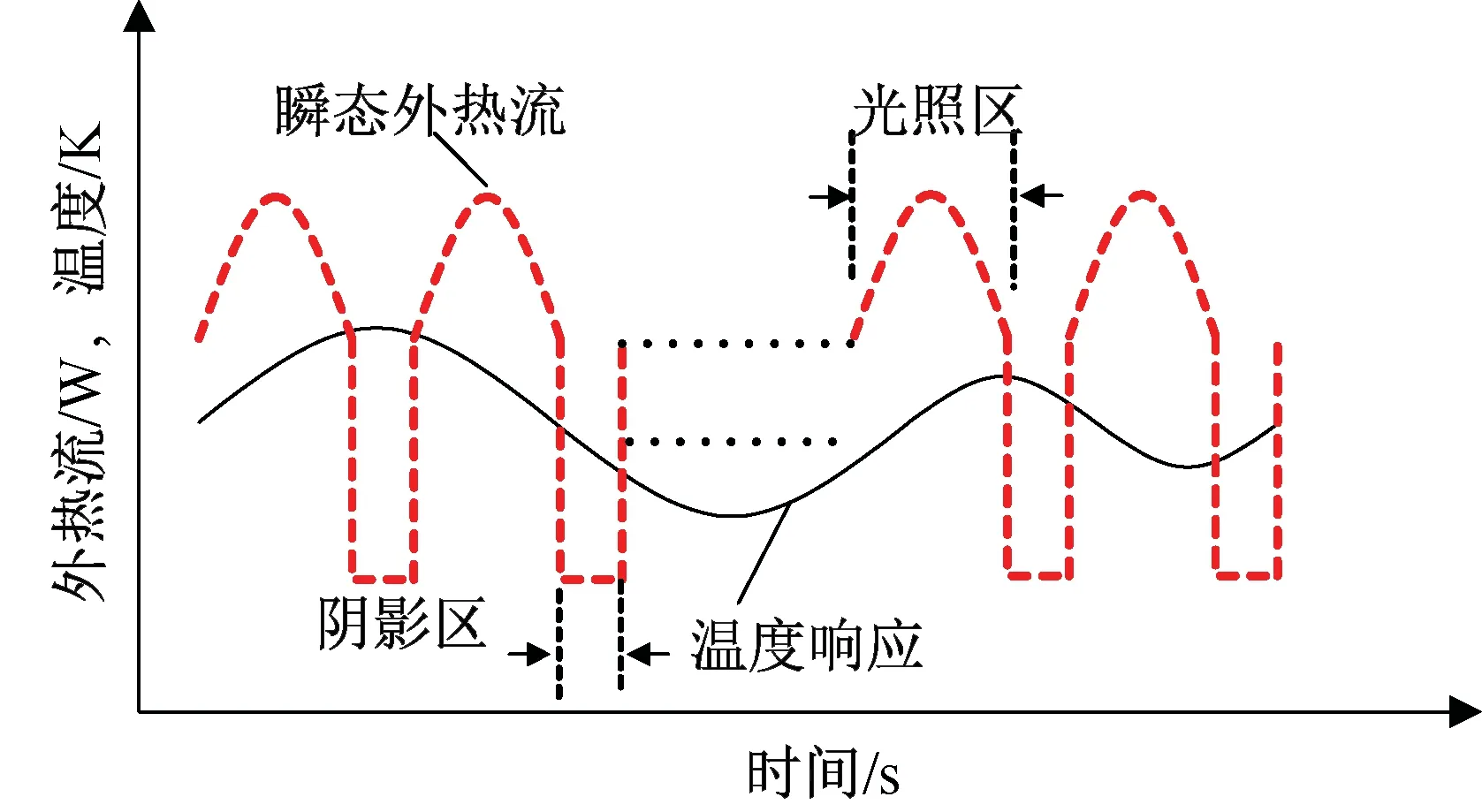
图2 卫星在轨吸收热流变化Fig.2 Change of absorption heat flow for on-orbit satellite

2 解析解推导

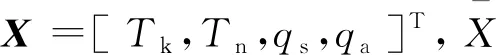
(3)

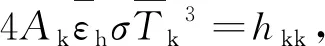
(4)

(5)

式中：qa+qi+qs=qw壳体节点吸收总外热流。

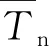
(6)

(7)

将式(1)，(2)分别与式(4)，(5)相减，并进行辐射项线性化处理后可得

(8)

(9)

将式(9)及其一阶求导结果代入式(8)中可得

(10)

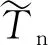
(11)

(12)

根据阻尼振荡系统特性的定义方法，小卫星不稳定传热的系统特性参数阻尼比ζ和自然频率ωn如式(13)，(14)所示，其中ζ>1说明传热系统热激励下振荡特性为过阻尼，不会出现共振峰值，即证明高低温工况能囊括卫星在轨温度动态变化范围。

(13)

(14)

(15)

3 基于解析解的小卫星动态传热特性分析

图3 阻尼比ζ随参数H和C变化曲线Fig.3 Change curve of damping ratio ζ with parameter H and C

为研究温度的波动特性随热参数变化规律，在控制理论中通常将此无因次量称为幅值特性[15]，它是系统对静态位移f0/K的放大倍数，表征了温度波动与外热流波动间的幅值传递关系。将ψd称为相位特性，它是温度波动相对外热流波动的延迟量，表征了两者间的相位传递关系。定义G为

(16)

式中：K=hkk。

图4 幅频特性曲线Fig.4 Characteristic curve of amplitude frequency

图5 相频特性曲线Fig.5 Characteristic curve of phase frequency

利用控制理论中常用的频域传递函数分析方法，对其幅频特性和相频特性进行分析[15]。依据G和ψd的表达式，得到幅频特性曲线和相频特性曲线如图4,5所示，图中阻尼比ζ=1.5,2,4,6,8,10，频率比λ∈(0,8]。从幅频特性曲线中可看出，增大阻尼比ζ和频率比λ，幅值特性下降。频率比的增大会增加热流的波动量与温度波动量间的相位差，当0<λ<1时，阻尼比ζ的增大会使延迟增大，当λ>1时，阻尼比ζ的增大会使延迟减小。从热控设计的角度来说，由内外结点传热系数hnk、外部节点对空间传热系数hkk及内部节点热容Cn，Ck决定的阻尼比ζ和自然频率ωn越大，越有利于削弱温度的波动振幅Bd。对于一个确定的热控系统来说，轨道周期越短，热流的波动频率ω越高，则幅值G越小。当到达热流确定时，光照面表面对到达热流的吸收特性和光照面所对应结点对空间辐射传热的传热系数，决定了静态位移f0/K，其值越小，则热流的波动振幅Bd越小。

4 数值验证

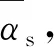
表1 数值计算参数范围

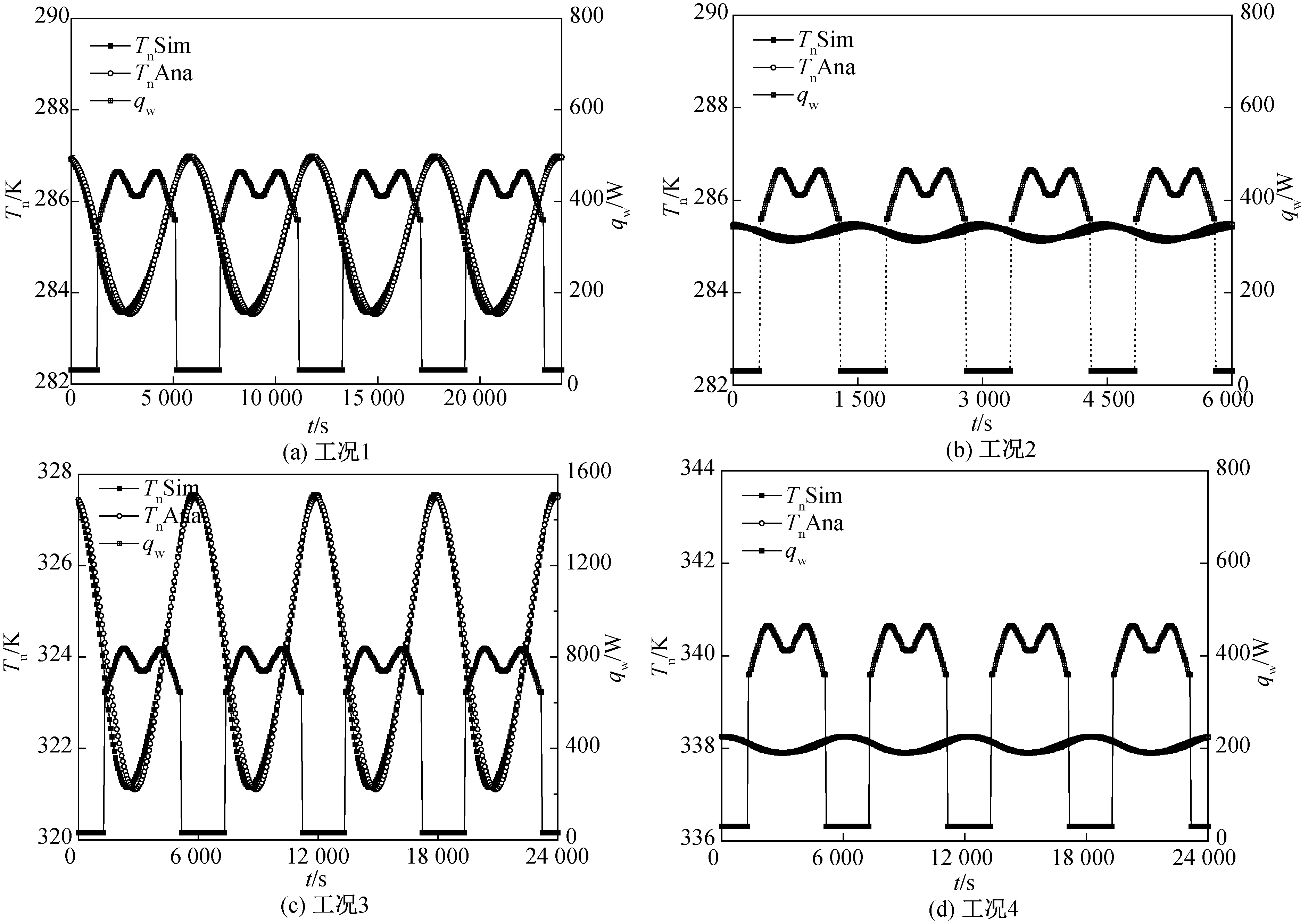
图6 数值解与解析解时域过程比较Fig.6 Comparison of time domain process between numerical solutions and analytical solutions

5 结束语

本文在小卫星双层集总参数模型下，对“热激励-温度响应”动态热平衡方程进行解析求解，并着重对其阻尼、相频及幅频特性进行了分析，得到主要结论如下：

1) 系统特性取决于系统阻尼比ζ和自然频率ωn，并证明系统热激励下振荡特性为过阻尼，传热系数比和热容比对阻尼系数的影响是对称的。阻尼比和自然频率定义与传热机理相符。

2) 对幅频和相频特性的分析表明，阻尼比ζ和频率比λ的增大以及静位移f0/K的减小均可降低温度的波动振幅，频率比的增大会增加热流的波动量与温度波动量间的相位差。当0<λ<1时，阻尼比ζ的增大会使相位差增大；当λ>1时，阻尼比ζ的增大会使相位差减小。

3) 利用四阶龙格-库塔方法对未简化的微分方程进行数值求解，验证解析解计算的准确性。结果表明，两种方法计算得到的典型工况下温度时域过程相符，幅频和相频特性曲线吻合较好。

在后续研究工作中将对本文研究结果进行验证，并进一步开展内热源变化下的小卫星动态传热特性研究。