考虑单框架控制力矩陀螺性能约束的小卫星姿态星载控制

李德婷，张元媛，王 华

(国防科技大学 空天科学学院，湖南 长沙 410073)

0 引言

随着空间技术的发展，小卫星因其功能密度高、研制周期短、发射灵活而成为新一代卫星的发展热点。姿态控制系统作为核心组成单元，是小卫星研究的重中之重。典型的姿态控制系统由喷气系统、磁力矩系统、动量轮等组成，广泛应用于转动惯量较大的航天器，但不适合转动惯量较小的航天器。单框架控制力矩陀螺(SGCMG)采用电能驱动，不需要消耗燃料，且具有较大的力矩输出能力，是小卫星姿态控制的理想设备[1]。

SGCMG虽具有优良的输出性能，但存在奇异问题，这使得姿态机动控制过程变得更加复杂。针对机动过程中的奇异失效问题，许多学者进行了相关研究。赵乾[2]采用伪谱法和直接打靶法混合求解策略，设计了单目标和多目标的轨迹规划模型，能满足SGCMG奇异饱和约束条件，但混合求解策略采用打靶法对奇异度量值进行优化，耗时较长，不能满足快速机动的需求。孙志远等[3]提出的基于自适应Gauss伪谱法的SGCMG 无奇异框架角轨迹快速规划方法，考虑了时间和能量加权的性能指标。该方法仅约束了终端的奇异度量，没有考虑机动环境中重力梯度力矩和轨道角速度的影响，且未考虑机动过程中的奇异情况，不具备稳定性，不适用于卫星在线姿态控制。

平坦微分理论是FLIESS等[4-5]在20世纪90年代针对非线性系统提出的概念，之后经过一系列的发展，在机器人、飞行器轨迹规划等方面得到广泛应用。本文将快速轨迹设计和抗干扰跟踪控制算法相结合，设计了一种星载在线控制方法。借鉴微分平坦理论在解决最优控制问题方面的研究成果，设计了一种姿态路径快速规划方法。该方法综合考虑了重力梯度力矩、轨道角速度等环境因素的影响，考虑了星体始末状态约束和SGCMG的动力学性能的约束，能快速求得满足约束条件的能量次优路径。通过将滑模控制与自适应相结合，获得了一种自适应滑模控制器。该控制器能克服外界扰动和陀螺执行误差对跟踪目标轨迹的影响。

1 动力学模型

1.1 姿态动力学模型

定义3个坐标系：惯性参考系、轨道坐标系和与航天器固联的体坐标系。采用修正罗德里格斯参数(MRP)描述姿态，MRP是姿态描述的最小实现，同时具有不易出现奇异和计算效率高的特点。与四元数相比，基于MRP的姿态计算在不损失计算精度的前提下计算量更小[6]，有利于提高姿态计算的效率。用MRP表示的姿态转移矩阵为

M(σ)=I3+

(1)

式中：I3为3维单位矩阵，[σ×]为矢量叉乘运算的反对称矩阵，即

(2)

用MRP表示的姿态运动学微分方程为

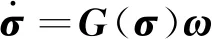
(3)

式中：ω为姿态角速度，G(σ)为

(4)

假设刚性小卫星在体坐标系下的惯量张量J为常值矩阵，则在体坐标系下卫星动力学方程为

(5)

式中：τgg为重力梯度力矩；u为姿态控制执行机构产生的控制力矩。

1.2 SGCMG动力学模型和奇异特性分析

SGCMG是由多个(一般3个以上)单框架控制力矩陀螺组成的具有三维输出能力的动量交换装置。若设每个力矩陀螺角动量的模相同且皆为h0，则陀螺群总角动量可表示为

H=h0(Asins+Bcoss)E

(6)

式中：A和B为与控制力矩陀螺中陀螺群的构型相关的安装矩阵；s为陀螺群的框架角矩阵，sins，coss为框架角正、余弦对角阵；E为元素都为1的3维单位向量。

由控制力矩陀螺对航天器作用的控制力矩为

(7)

C(s)=Acoss-Bsins

(8)

在SGCMG工作的过程中，系统力矩如果持续朝一个方向输出，则角动量在某个方向上的值不断积累，就有可能导致角动量值达到SGCMG系统最大角动量，这种情况被称为角动量饱和，是SGCMG失效的一种形式。金字塔构型的SGCMG的角动量饱和包络面为如图1所示的具有8个凹陷的不规则球面，球体半径约为

Hmax=3.3h0

(9)

图1 金字塔构型控制力矩陀螺角动量饱和面Fig.1 Envelope surface of pyramid configuration

当SGCMG系统框架角处于某些特定状态时，期望力矩与控制力矩正交，此时SGCMG系统无法输出期望力矩，失去控制能力，这种现象称为奇异失效。当期望力矩ut和安装方向gi平行时，该陀螺所有状态均奇异；当期望力矩ut和安装方向不平行时，ut与gi方向存在夹角，如图2所示，则每个陀螺的奇异角动量有2个方向[7]，奇异角动量为hi=±(gi×ut)×gi/‖gi×ut‖。

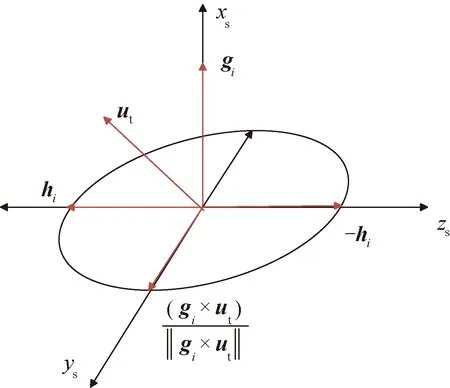
图2 控制力矩陀螺奇异机理分析Fig.2 Mechanism analysis of SGCMG

在进行轨迹规划时，需要根据当前的框架角对奇异状况作出判定，即需要定义一种度量不同框架角组合所对应奇异程度的奇异状态量。根据框架角奇异的原理，即当C-1不存在时发生奇异，使用奇异度量[8-9]来衡量当前框架角的奇异状态，即

D=det(CCT)

(10)

当D=0时，系统处于奇异状态，D越大，离奇异点就越远。

2 在线控制方法设计

2.1 基于平坦微分理论的姿态轨迹规划

2.1.1 微分平坦系统

FLIESS于1992年首次提出了微分平坦理论，即采用微分代数来描述一个微分系统，将对微分系统中微分方程的求解转化为对代数多项式参数的求解，从而减少系统中的积分运算，缩短计算时间。考虑非线性系统

(11)

式中：x∈Rn，u∈Rm，且m≤n。根据微分平坦理论，如果能找到一个平坦输出z∈Rm，将式(11)中所有的输入量和状态量都用z和它的有限次导表示出来，则称这个系统为微分平坦系统[10]，即

(12)

文献[11]已证明，由姿态运动学方程(3)和姿态动力学方程(5)描述的姿态控制系统是以(σ1,σ2,σ3)为平坦输出的微分平坦系统。本文的研究在该系统的基础上加入SGCMG操纵系统，即在该系统中加入状态量框架角(s1,s2,s3,s4)。SGCMG的操纵律即是根据指令力矩来合理分配框架角的转速，使陀螺群的输出力矩与航天器姿控系统要求的指令力矩相等。因SGCMG是一个冗余系统，利用式(1)，(2)反解求得的框架角速度不唯一，故考虑框架角的姿态控制系统不具备微分平坦属性，无法直接基于微分平坦开展轨迹设计。为扩展系统的平坦属性，约束框架角为最优伪逆操纵律[12]的解，即定义框架角为

(13)

框架角可由平坦输出唯一表示，则系统是微分平坦系统。

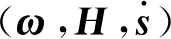
(14)

式中：τgg为重力梯度力矩；ωo为卫星的轨道角速度；τgg=3(ωo)2[i×]Ji，其中，i为地心与卫星质心连线方向的单位矢量。

2.1.2 平坦输出基函数

平坦输出参数化是轨迹优化的关键，通过参数化将含有微分的最优控制问题转换为非线性规划问题[13]，不同的基函数对优化效果和计算效率有不同的影响。

受文献[14]的启发，采用虚拟域的方法，通过分离时间域与空间域，使轨迹可用不同的速度场描述。引入虚拟域参数γ，则γ与时间域t相互转换，即

(15)

给定控制点p0,p1,p3,…,pn，则由这些控制点约束的虚拟域的Bezier多项式p(γ)为

(16)

式中：βi,n(γ)为第n个伯恩斯坦多项式，即

(17)

Bezier多项式的性质[15]为

(18)

每个MRP都可在虚拟域γ∈([0,1]中用Bezier多项式表示，即

(19)

(20)

式中：j=1,2,3。

对于有NB个端点约束的Bezier多项式，其控制点的个数要求n≥NB+1，则至少有1个控制点参数可作为优化变量对路径进行优化。

2.1.3 非线性规划模型

本系统中的状态量和控制量都可由平坦输出(σ1,σ2,σ3)表示，通过对平坦输出参数化，将系统中的状态量和控制量都由控制点待定的Bezier多项式表示出来，则轨迹规划问题被转化为对Bezier曲线的控制点求解的非线性规划问题。

对于不同的任务要求，非线性规划问题的性能指标不同。本文以最小能量为优化目标，定义性能指标

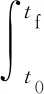
(21)

minQ=Q[p0,p1,p3,…,pn]

(22)

(23)

式中：p0,p1,p3,…,pn为Bezier曲线的一组控制点。

2.2 姿态跟踪控制算法设计

2.2.1 基于跟踪误差的姿态动力学模型

基于微分平坦理论设计的姿态轨迹，虽然考虑了轨道角速度和重力梯度力矩的影响，但在实际机动过程中，仍受到不确定的环境力矩和干扰力矩的影响。需要采用合适的控制算法，在环境干扰的影响下，于有限的时间内使实际姿态轨迹快速收敛至所规划的开环最优轨迹上。

(24)

根据式(24)，定义姿态误差MRPσe[16]，有

(25)

同样，使用角速度偏差ωe来表示实际角速度ω和目标角速度ωc之间的偏差，有

(26)

(27)

将式(5)代入式(27)，可得关于角速度偏差ωe的运动学微分方程为

(28)

式中：τ=τgg-u+τo，τ为控制力矩、重力梯度力矩和气动力矩的总和；d为环境的干扰力矩。

根据式(3)可列出关于姿态偏差σe和角速度偏差ωe的运动学微分方程，即

(29)

对式(29)求导，得到

(30)

对式(30)左乘JG-1，再将式(28)代入，整理得到

(31)

式中：

(32)

2.2.2 滑模控制器设计

定义滑模控制器的切换函数为

(33)

式中：λ为三阶正定对角矩阵。

趋近律采用指数趋近律[17]，形式为

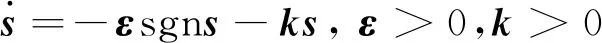
(34)

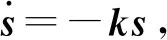
对式(33)求导，代入式(34)中整理后可得

(35)

将式(35)代入式(31)，化简得到滑模控制方程为

A1kλσe+(A3-A1εsgns)

(36)

式中：εsgns为鲁棒项，用于克服不确定的干扰力矩的影响。但是，由于使用了阶跃的切换函数，使得产生的控制信号产生抖振。考虑采用连续切换的双曲正切函数来代替阶跃函数，从而降低滑模过程中的抖振[18]。设计鲁棒项γtanh(βs)代替εsgns。其中，将向量的双曲正切函数性质定义为[19]

tanh(q)=diag(tanh(q1),tanh(q2),tanh(q3))

(37)

式中：γ和β为大于0的参数。γ与环境干扰力矩的上界有关，干扰上界越大，γ取值也越大。β的取值和边界层Δ相关，β=1/Δ。边界层具有如下性质：在边界层外，鲁棒项采用切换控制，系统能以较快的速度到达切换面；在边界层内，鲁棒项采用反馈控制，可减小抖振效应。则控制器设计为

A1kλσe+[A3-A1γtanh(βs)]

(38)

3 仿真算例

卫星转动惯量为J=diag(36,36,60)kg·m2，在高度约为380 km的圆轨道运行，轨道角速度近似于常值0.001 1 rad/s。SGCMG选用由4个陀螺组成的金字塔构型，如图3所示。

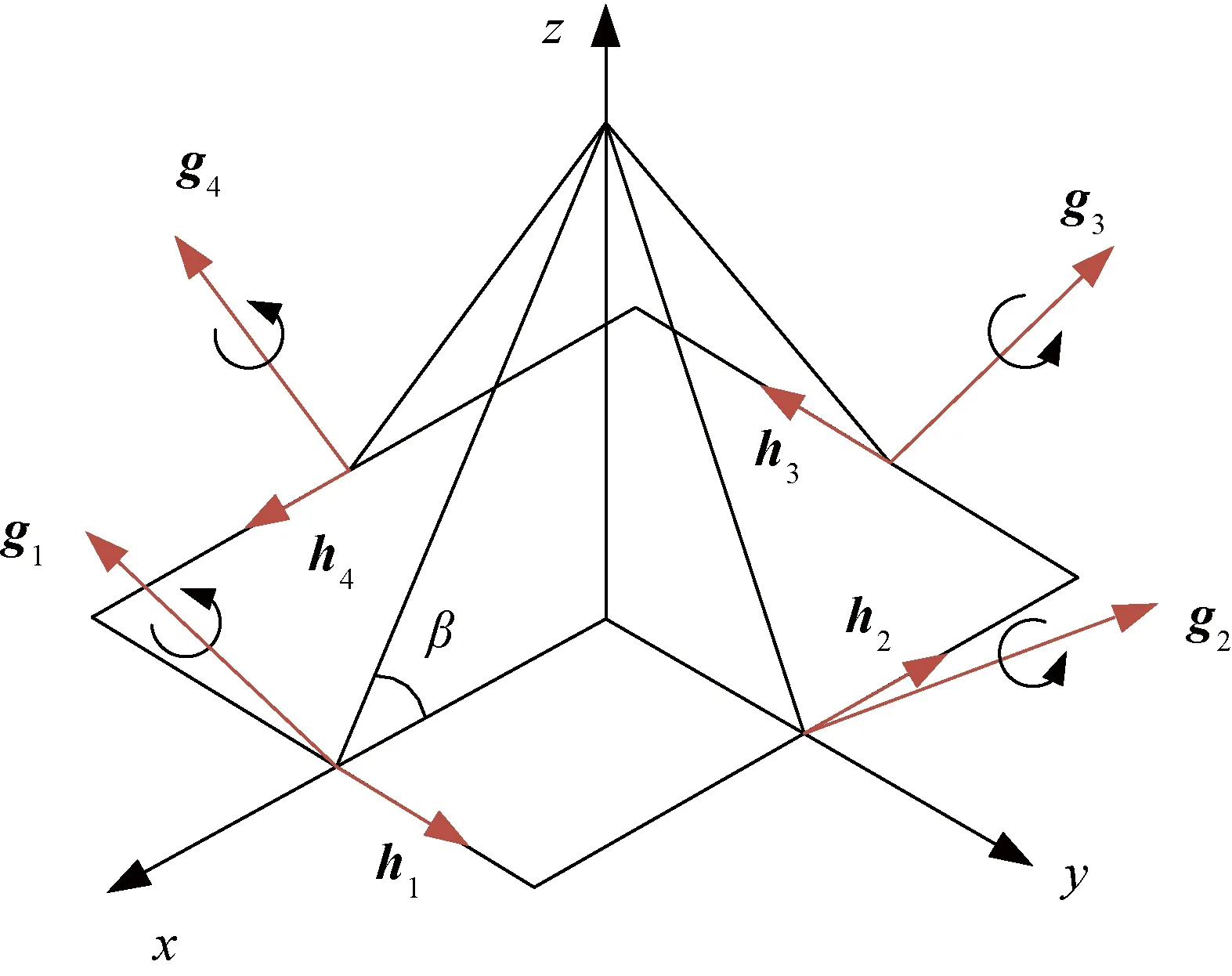
图3 金字塔构型控制力矩陀螺机构示意图Fig.3 Schematic diagram of pyramid configuration SGCMG

系统安装倾角β=54.13°，gi(i=1,2,3,4)为每个陀螺的框架安装方向，框架绕安装方向逆时针旋转。图3中，hi(i=1,2,3,4)为框架角为0°时输出角动量的方向。根据构型，安装矩阵为

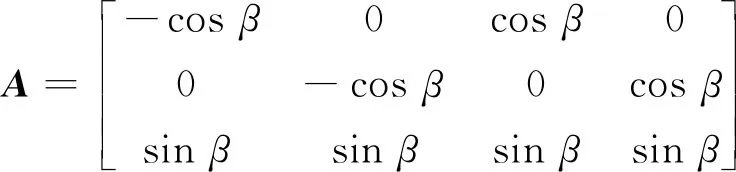
(39)

(40)

单个陀螺角动量大小为1.5 N·ms，根据式(3)，角动量幅值为4.95 N·ms。可输出的最大控制力矩为5 N·m，最小奇异测度为1.2，机动时间为50 s，机动起始端点约束见表1。

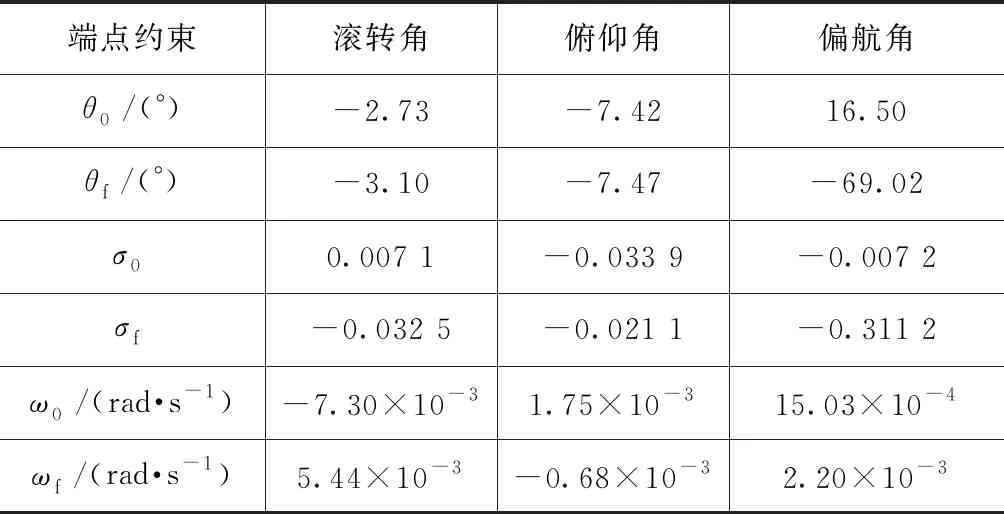
表 1 姿态端点约束

仿真试验所用的电脑配置为Inter(R) Core(TM) i7CPU，主频为3.6 GHz，内存为4 GB，仿真编程环境为MATLAB R2016b。采用SQP算法进行非线性优化，Bezier曲线的控制点个数分别取5，6，7，8(多项式阶次分别为4，5，6，7)。优化得到的轨迹性能指标和所需计算时间见表2。由表可知，随着控制点增多，优化得到的轨迹性能指标越优，但所需的计算时间也越多，其中，当控制点取到最小值5时，规划时间仅需0.7 s。

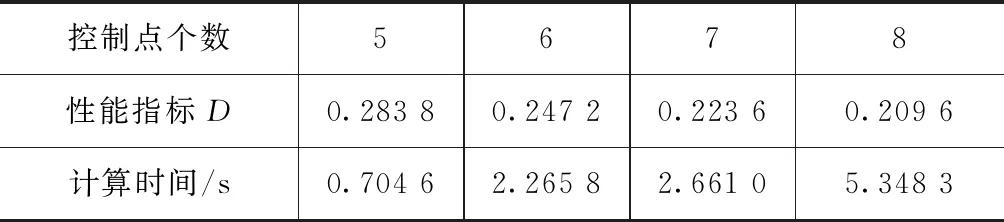
表 2 不同控制点个数轨迹规划结果比较

取5个控制点优化所得的姿态路径作为目标路径，如图4所示，采用滑模跟踪算法进行姿态控制。控制器参数选取为

(41)

图4 4阶最优轨迹Fig.4 Optimal trajectory in 4 orders

误差MRP的变化曲线如图5所示。由图可知：为完成初始姿态捕获，前6 s控制方式为变结构控制，有抖振现象出现；当误差足够小后，控制方式变为反馈控制，实际姿态能以较小的误差平稳跟踪目标姿态。控制力矩随时间变化情况如图6所示。由图可知：在变结构控制阶段，控制力矩较大；从变结构控制转为反馈控制后，控制力矩以较小量完成姿态跟踪。机动全程控制力矩小于5 N·m，符合SGCMG力矩输出能力。机动全程MRP误差在3×10-3以内，在反馈控制阶段，MRP误差在2×10-4以内。控制算法能很好跟踪期望姿态路径。奇异度量值的变化曲线如图7所示。由图可知：在机动过程中，奇异测度值始终大于1.2，SGCMG一直处于远离奇异的状态，具有稳定的控制能力。机动全程的角动量曲线如图8所示。由图可知：角动量一直小于2 N·ms，处于角动量饱和上限以内。

图5 误差修正罗德里格斯参数Fig.5 Error MRP

图6 控制力矩随时间变化Fig.6 Control force versus time

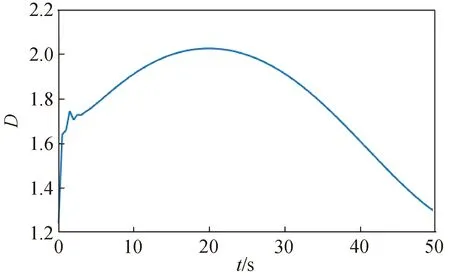
图7 奇异度量随时间变化Fig.7 Singularity parameter versus time

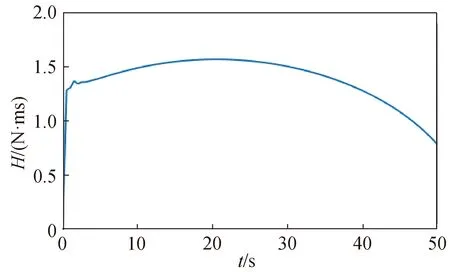
图8 角动量值随时间变化Fig.8 Angle momentum versus time

4 结论

本文主要针对以SGCMG为姿态执行机构的小卫星的姿态机动问题，基于SGCMG力矩输出效率高，但具有奇异饱和性能的特点，设计了基于平坦微分理论的快速参考轨迹规划方法和滑模控制器相结合的控制方法。该方法考虑了轨道角速度、重力梯度力矩和空间扰动力矩的影响，在约束范围内具有很好的控制精度，且所需的计算时间少，能满足星载在线控制的需求。该方法基于平坦微分理论将最优控制问题转化为非线性优化问题，提高了计算效率。与文献[2]中需要6 min计算时间相比，该算法能在0.8 s内找到光滑无奇异的姿态轨迹，大大提高了规划效率；与文献[3]中仅考虑端点奇异状态的规划方法相比，该算法考虑了机动过程中的奇异状态，能保证在机动过程中不会陷入奇异，更具稳定性，可满足星载在线控制的需求。采用具有NB个控制点的Bezier多项式来表示轨迹，保证姿态轨迹NB-1阶连续，所设计的的轨迹具有角速度和角加速度连续、轨迹平滑的优点。本文算法能在有限干扰的影响下以小误差跟踪期望姿态，保证了跟踪精度，使机动全程控制力矩、角动量、奇异测度都在限定范围内。然而，多项式对曲线的表述能力有限，这也导致优化得到的姿态轨迹一般是能量次优解。在后续研究中，将寻找更具完备性的多项式来描述平坦输出。