某二级斜齿圆柱齿轮减速器NVH性能预测及优化
2019-07-05魏显坤杨兴国赖天华
魏显坤,杨兴国,赖天华
(1.重庆工商职业学院, 重庆 401520; 2.重庆耐世特转向系统有限公司, 重庆 401520)
当前,随着对噪声污染认识水平的提高,人们对机械设备的NVH(Noise Vibration Harshness)性能也空前的重视。在现代工业中,齿轮以其高的效率、稳定的传动比以及紧凑的结构等在机械传动中起着至关重要的作用。因此,减速器在产品设计阶段预测NVH性能和优化具有重要的现实意义。
国内外学者就齿轮系统减振降噪已经开展了广泛的研究工作。对于齿轮-转子系统振动响应的研究,提出了基于齿轮副集中参数模型的齿轮刚度激励、啮合冲击激励模拟方法[1-2],对齿轮-转子系统进行固有特性及动态响应的数值仿真分析[3],齿形修型对传动误差及
动态响应的影响[4-7]。对于壳体的动态特性及辐射噪声的研究,应用声固耦合的方法对壳体进行声辐射分析[8],就各面板对声场声压贡献度分析[9],应用能量统计方法对壳体进行振动噪声预测[10]。
1 减速器的振动噪声与传播路径
减速器的噪声主要表现为敲击噪声和啸叫噪声。前者是由于齿轮副存在间隙和动力源输入的激励为扭转振动激励而产生的,然而本减速器是以三相异步电机为动力源,其输出转速非常平稳,所以本减速器的敲击噪声理论上没有或很小。而后者主要是由于齿轮的传动误差引起的,其原因有两方面:一是齿轮本身的精度等因素影响;另一方面是由齿轮啮合错位造成的,啮合错位是由轴、轴承的变形导致的。 减速器振动噪声传播可分为三部分:振动经齿轮、轴、轴承等传到壳体,通过壳体外壁振动而辐射到箱外空气中,形成第一次空气声;箱内噪声激发壳体振动,通过壳体辐射到箱外空气中,形成第二次空气声;箱内噪声通过各种缝隙传到箱外。实验表明,减速器噪声中约90%~95%是通过振动传递,最后由齿轮箱壳体振动而辐射到箱外的[11]。振动噪声传递路径如图1所示。
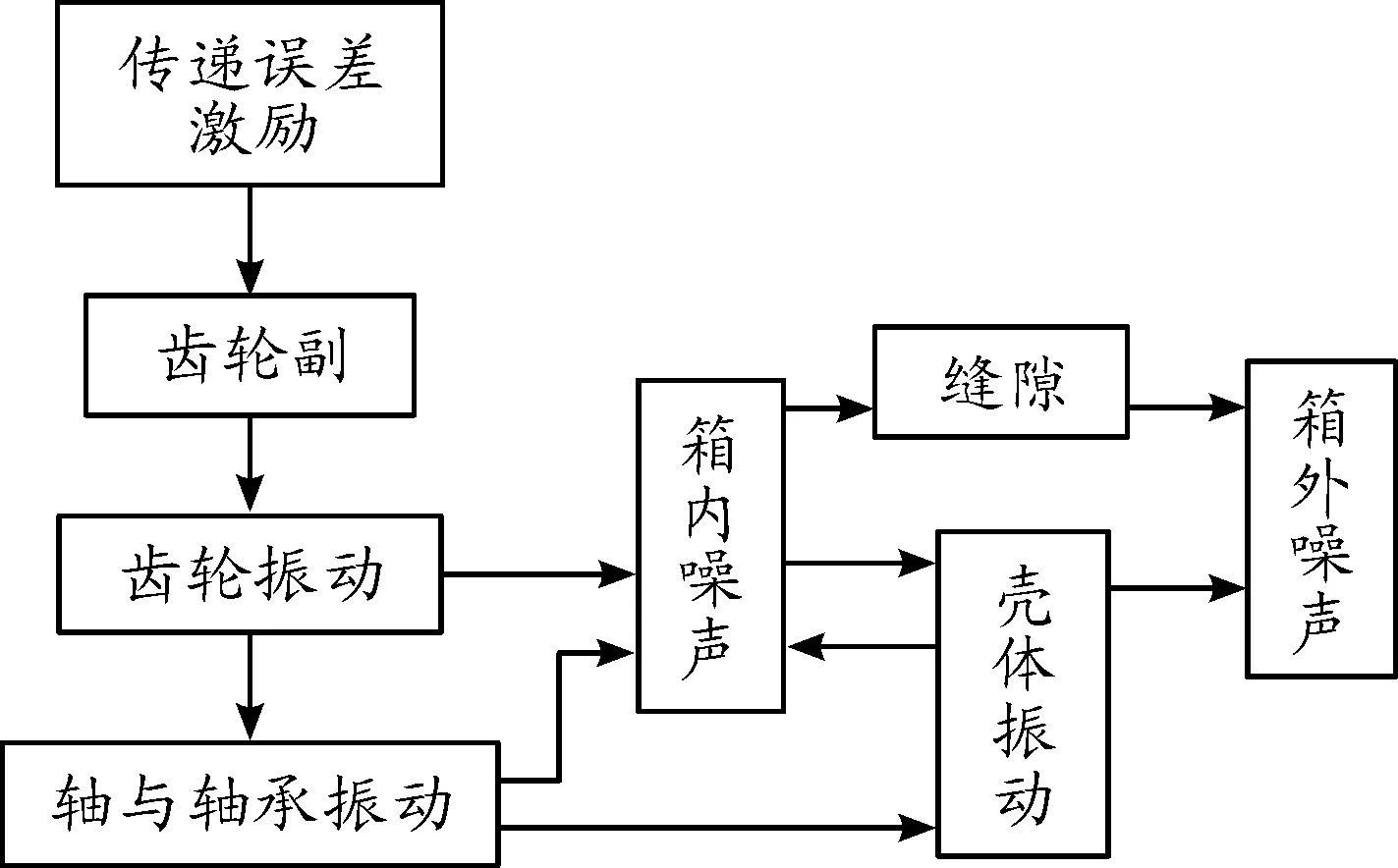
图1 振动噪声传递路径
2 齿轮-转子系统动态分析
2.1 齿轮-转子系统Romax模型
在Romax软件中,根据设计参数依次完成轴的建模、齿轮建模、轴承的选择。齿轮建模分为概念建模和详细建模,详细建模包括定义齿轮的精度等级、表面粗糙度、变位系数和齿侧间隙等。然后装配成齿轮-转子系统模型,如图2所示。
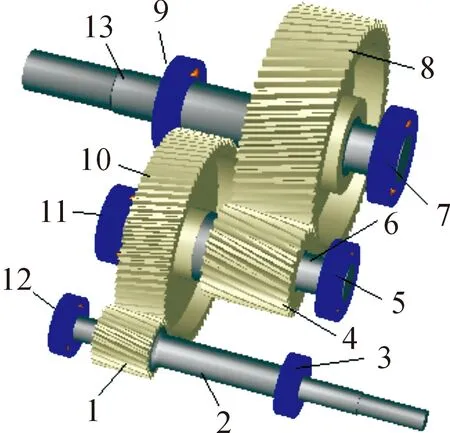
1.第一级主动齿轮; 2.输入轴; 3.轴承2; 4.第二级主动齿轮; 5.轴承4; 6.中间轴; 7.轴承6; 8.第二级从动齿轮; 9.轴承5; 10.第一级从动齿轮; 11.轴承3; 12.轴承1; 13.输出轴;
图2 齿轮-转子系统模型
2.2 传动误差激励
传动误差是齿轮副实际啮合点与理论啮合点的偏差,可以表示为一对齿轮节圆相切点的线性偏差,所以定义传动误差为
TE=θc*rc-θz*rz
(1)
式中:θc为从动齿轮转角;θz为主动齿轮转角;rc为从动齿轮基圆半径;rz主动齿轮基圆半径。
在Romax软件中进行齿轮-转子系统动态分析时,是以齿轮传动误差为激励的,同时考虑啮合综合刚度和系统固有特性的影响。齿轮副啮合时载荷计算公式
{p}={po}+[k′]{e}
(2)
式中:{p}为载荷阵列;{po}为静态载荷阵列;[k′]为啮合综合刚度矩阵;{e}为传动误差激励。
本研究在校核齿轮、轴承以及轴的疲劳寿命和静态分析后,计算得到两级齿轮副传动误差如图3所示。

图3 传动误差
第一级齿轮副传动误差值在-1~1 μm,其中最大值为0.94 μm,最小值为-0.82 μm,相差1.76 μm。第二级齿轮副传动误差值在3.3~4 μm,其中最大值为3.92 μm,最小值为3.37 μm,相差0.55 μm。产生传递误差的原因有齿轮的精度误差、表面粗糙度以及齿轮轴和轴承变形引起的啮合错位。
2.3 齿轮-转子系统模态分析
应用Romax软件中的NVH模块,可以计算得到齿轮-转子系统各阶模态的固有频率和振型,如表1所示。本减速器的齿轮-转子系统的前25阶模态的固有频率范围为182~4 209 Hz,若激励频率与齿轮-转子系统的固有频率重合容易引发共振,该频率下的激励将被放大后传递到壳体上。
2.4 齿轮-转子系统振动响应
在两级齿轮传递误差的激励下,齿轮-转子系统发生振动,图4分别是输入轴和输出轴安装第一级主动齿轮和第二级从动齿轮处的响应加速度曲线。其中,振动加速度出现在频率为3 366 Hz和2 330 Hz处,值为743 m/s2和69.6 m/s2,分别对应齿轮-转子系统的第19阶和第21阶固有频率。
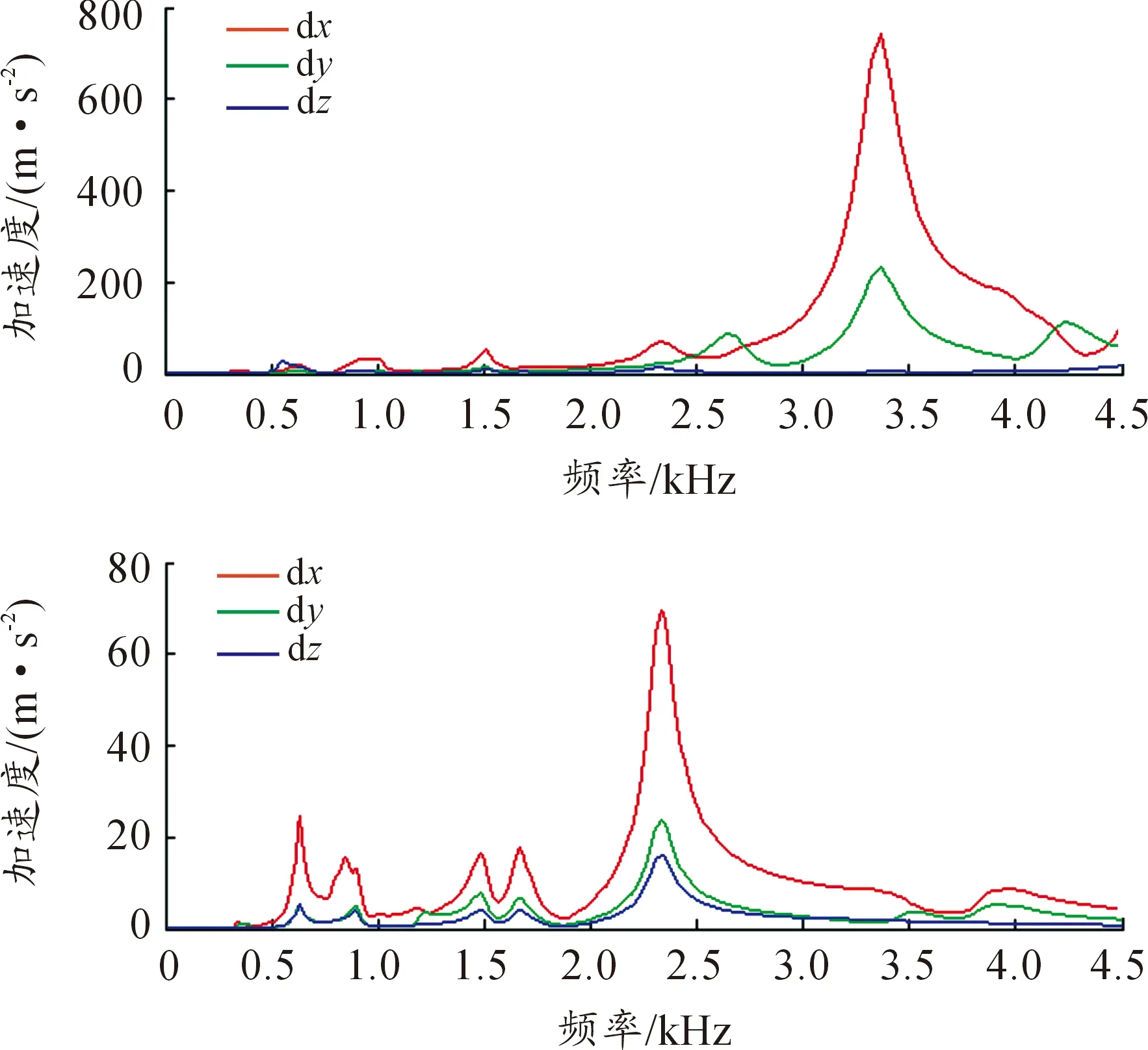
图4 输入/出轴振动加速度幅值谱
齿轮-转子系统的振动会向周围空间(箱内空间)辐射噪声,由于辐射的表面积较小和壳体等密封件的隔声作用,该噪声传递到箱外很少,不给予考虑。本研究重点关注轴承传递给壳体的作用力,图5是轴承1~6在X轴、Y轴和Z轴的作用力幅值谱。可以看出,各个峰值都出现在齿轮-转子系统的固有频率处,说明齿轮-转子系统的固有特性对轴承作用力影响巨大。
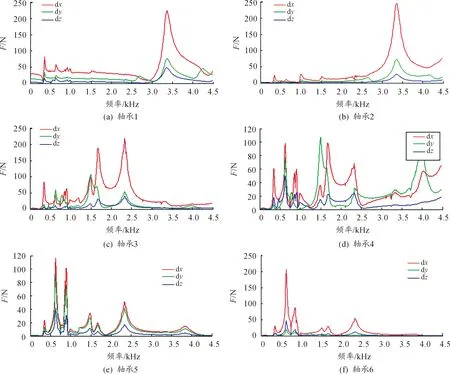
图5 轴承作用力幅值谱
3 壳体的振动分析
3.1 模态分析
模态分析主要用于确定零件或部件的固有特性,即各阶模态。壳体是减速器声辐射的主要部件,其固有特性对整个减速器的NVH性能起着至关重要的作用。通过模态分析,可以得到壳体的固有频率和振型,为减速器NVH性能预测和优化提供重要帮助和参考。模态振型如图6所示。
对于多自由度线性定常系统,建立结构的动力学方程为

(3)
式中:[M]为总质量矩阵;[C]为总阻尼矩阵;[K]为总刚度矩阵;{f}为节点等效载荷列阵;{x}为节点位移列阵。
在结构的动力学方程中,令[C]=0和{f}=0,得到无阻尼自由振动方程为
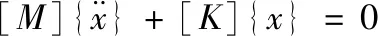
(4)
式(4)的特征方程为
(5)
求解特征方程的前n个特征值,这n个特征值就是结构的前n阶固有频率。
本文将Creo Parametric建立的减速器壳体三维模型导入前处理软件ANSA中建立有限元模型,然后应用ANSYS求解器进行计算并进行后处理。本文计算壳体在约束条件下且固有频率在4 500 Hz内的模态,表2是壳体前20阶固有频率及振型描述。
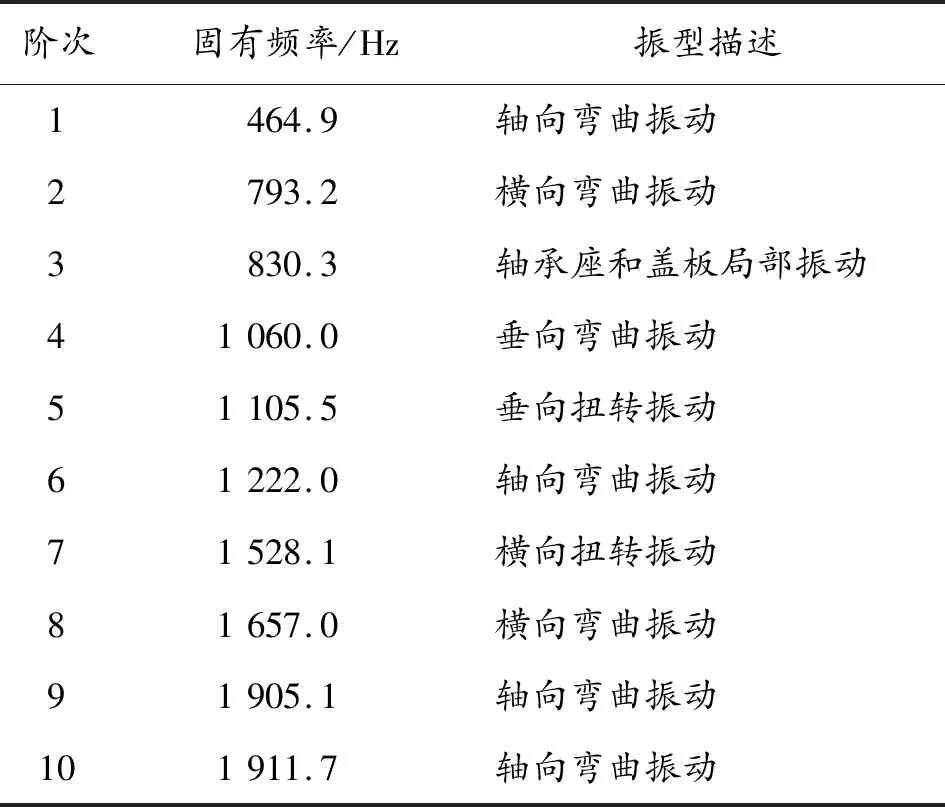
表2 壳体前20阶约束模态
3.2 振动响应分析
减速器壳体是由大板件组成,在外在激励下容易激发大的振动,声辐射效率较高,是加速器声辐射的主要部件,所以它的振动是决定减速器NVH性能的关键。如图1所示,壳体振动由两部分组成:一是箱内噪声传到壳体内壁上,激发壳体振动,同时壳体振动也向箱内辐射噪声;二是振动经齿轮、轴和轴承传递到壳体上,激发壳体振动。因为减速器壳体刚度较大,声音激起的振动非常小,所以壳体的振动主要是后者。

图6 模态振型
本研究以2.4节的轴承作用力及其相位作为激励,应用模态叠加法计算壳体的振动响应,得到的结果可以作为边界元法计算壳体声辐射的边界条件。图7是箱盖后端某点的振动加速度频谱和箱盖前端某点的振动加速度频谱,后点振动加速度在3 370 Hz时有最大值为101.7 m/s2,主要是轴承1和轴承2的激励引起的,其他峰值频率分别对应壳体的第1阶、第2阶、第4阶、第8阶、第9阶、第14阶及第39阶固有频率;前点振动加速度在3 320 Hz时有最大值为190.8 m/s2,主要是壳体的第29阶模态和轴承作用力引起的,其他峰值频率分别对应壳体的第1阶、第2阶、第4阶、第8阶、及第14阶固有频率。
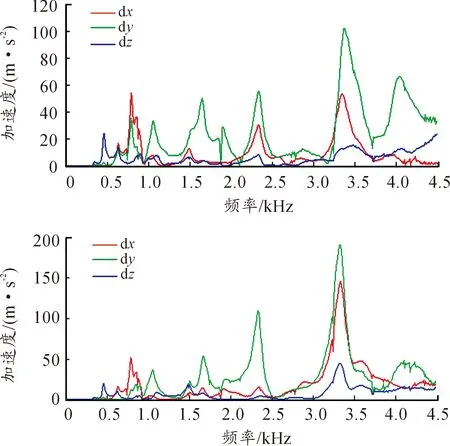
图7 振动加速度幅值谱
4 壳体声辐射预测
4.1 ATV和MATV方法
在小压力扰动情况下,可以认为声学方程是线性的,因而可以将结构表面的振动和某场点声压之间建立某种线性对应关系,把结构表面离散成有限个单元,这样在某场点的声压为
p={ATV(ω)}T{νn(ω)}
(6)
式中:ATV(ω)为声传递矢量(Acoustic Transfer Vector);νn为结构表面法向振动速度;ω为圆频率。
通过声传递矢量,可以在声场中某场点声压与模型振动速度之间建立联系,ATV的物理意义可以理解为节点或单元在某频率下的单位模型振动速度在某场点上引起的声压值。
另外,结构振动位移响应可以通过模态线性叠加得到,即
{x}=Ω*{MRSP(ω)}
(7)
式中:{x}为结构位移;Ω为结构模态矩阵;MRSP(ω)为模态参与因子向量。
将结构表面振动的位移向量{x}投影到结构表面的法向上,就可以得到结构在法向的振动速度
{vn}=jωΩn{MRSP(ω)}
(8)
式中Ωn是结构振动模态在结构表面法向分矢量组成的矩阵,由此可以得到声场中任意场点的声压为
p={ATV(ω)}T·jωΩn·{MRSP(ω)}=
{MATV(ω)}T·{MRSP(ω)}
(9)
式中{MATV(ω)}T为模态声传递矢量(Model Acoustic Transfer Vector),{MATV(ω)}T的表达式为
{MATV(ω)}T=jωΩn·{MRSP(ω)}
(10)
MATV的物理意义为单元或节点在特定频率下的单位模态响应在声场中某场点处引起的声压值。
4.2 壳体的声传递矢量
本研究在LMS Virtual.lab软件中创建的边界元模型,声学网格采用线性网格,其最大尺寸小于最高计算频率(4 500 Hz)点处的波长的六分之一;在壳体下方10 mm处创建对称面,用来模拟地面;声速为341 m/s,空气密度为1.21 kg/m3,并生成ISO声场,如图8所示,该声学边界元模型共有19个场点组成。图9是频率为640 Hz、790 Hz、1 060 Hz、1 660 Hz、2 330 Hz以及3 300 Hz时声学网格与19号场点的声传递矢量云图。可以看出在低频时,底板表面的声学传递矢量较大,而高频时箱盖表面的声学传递矢量较大。

图8 声学边界元模型

图9 声传递矢量云图
4.3 壳体的声辐射
声功率是声源在单位时间内辐射的声能量,是描述声源声能量大小的量。在声学中,声功率用声功率级表示
LW=10lg(W/W0)(dB)
(11)
式中:W0为基准声功率;在空气中取W0为10-12W。
图10为壳体辐射的声功率谱,峰值频率(Hz)和声功率级(dB)值分别为:(460,88.39)、(640,91.75)、(790,91.04)、(1 060,89.66)、(1 480,89.55)、(1 660,88.29)、(2 330,88.1)以及(3 300,92)。这些峰值都是壳体的强烈振动造成的,它们分别对应壳体的某阶固有频率或激励的峰值频率。其他频率下的声功率级集中在70~90 dB间,可以看出壳体辐射的声能量较大,其原因是两级齿轮啮合状态很差,造成大的传动误差造成的。
图11为第19号场点声压谱,峰值频率(Hz)和声功率级(dB)值分别为:(460,86.26)、(640,19.75)、(910,80.38)、(1 060,90.85)、(2 030,85.13)、(2 290,85.16)以及(3 300,88.81)。图12是第1~9号场点声压-频率谱,图13是第10~18号场点声压-频率谱,图14分别为频率为460、640、790、1 060、1 480、1 660、2 330以及3 300时的声场声压分布云图。

图10 声功率谱

图11 第19号场点声压谱
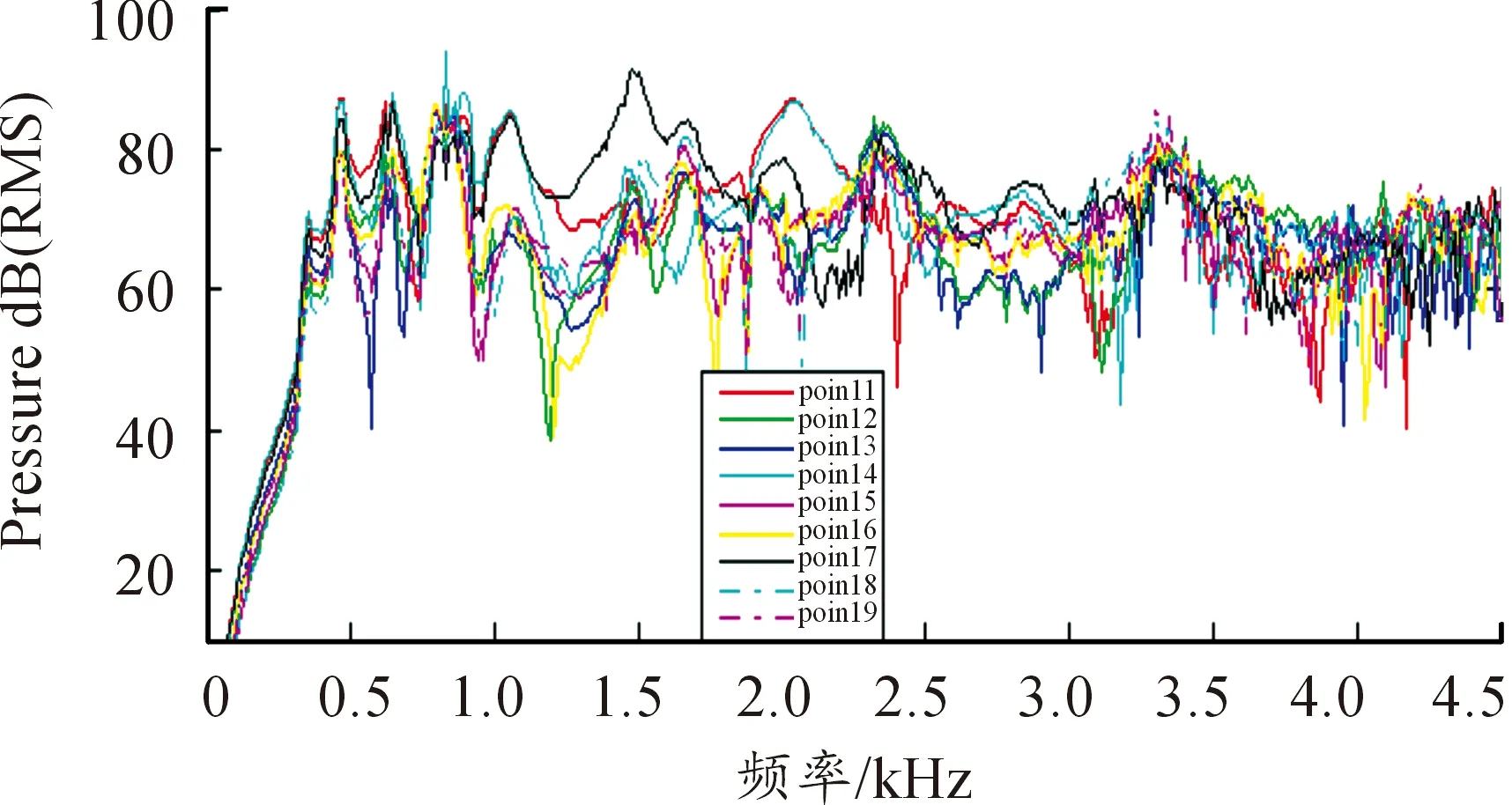
图12 第1~9号场点声压-频率谱
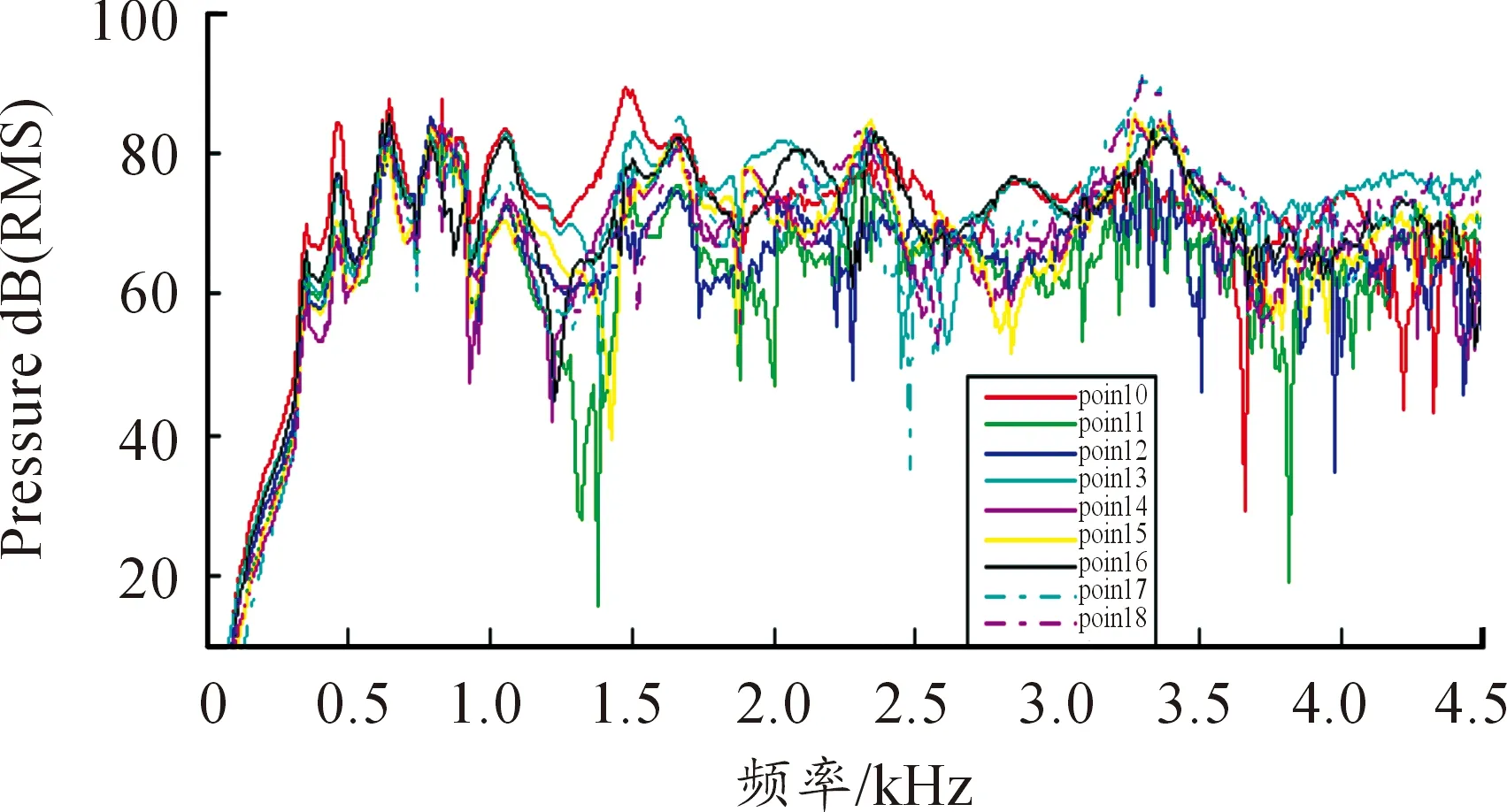
图13 第10~18号场点声压-频率谱
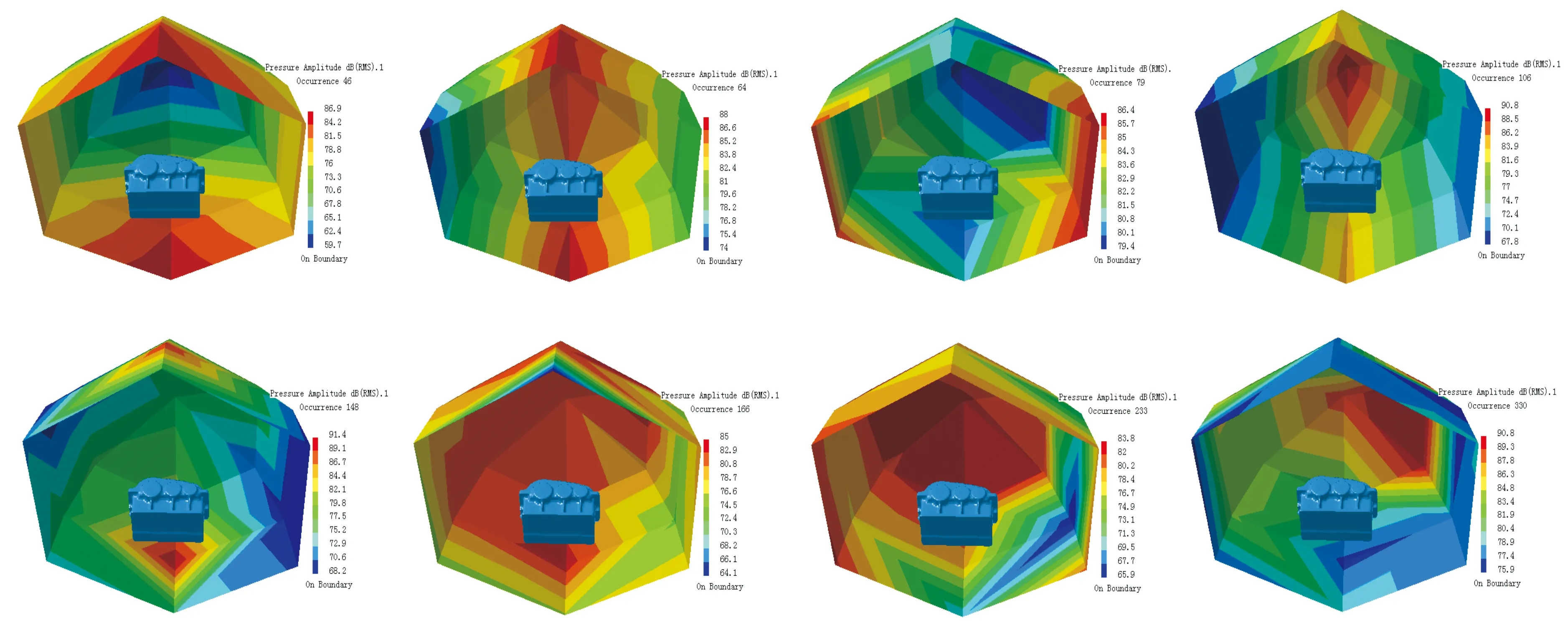
图14 声场声压分布云图
总的来说,该减速器的噪声辐射较大,如不加以优化,产品会有较大噪声的风向,所以必须对其进行NVH性能优化。
5 减速器NVH性能优化
5.1 轴的优化
在齿轮-转子系统中,从研究齿轮激励入手,可以简化成质量-弹簧振动系统,如图15所示,K是等效弹簧刚度,M是等效质量。当质量块振动时,传递到地面的力为F=Kx=Md2x/dt2,在相同的位移激励下,等效刚度和等效质量越大,力就越大。所以可以通过减小轴的刚度,从而减小齿轮-转子系统轴承作用力。
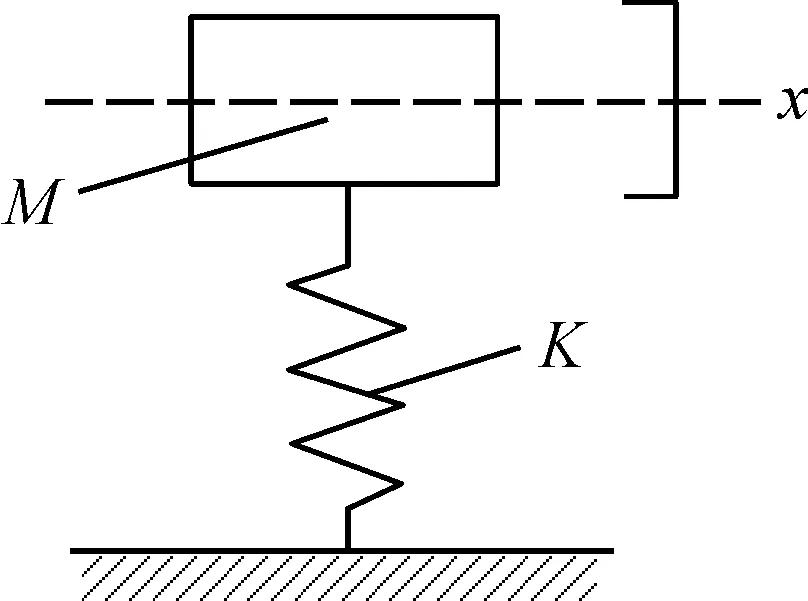
图15 齿轮-转子系统的简化示意图
本研究在满足齿轮-转子系统对轴强度要求的条件下,减小输出轴和输入轴的刚度。将第一级主动齿轮和轴承3之间修改成直径20 mm、长94 mm和直径35 mm、长6 mm的两段。将第二级从动齿轮的固定台阶和轴承6之间修改成直径46 mm、长10 mm和直径35 mm、长61 mm。从结果看,第一级齿轮副传动误差增大而第二级齿轮副传动误差基本不变,如图16所示,第一级齿轮的传动误差的最大最小值分别为-5.13 μm和-2.41 μm,相差2.72 μm,增加了54.5%,而第二级齿轮的传动误差的最大最小值分别为3.65 μm和3.12 μm,相差0.53 μm。这是由于减小轴的刚度使轴的静态变形增大,从而影响齿轮副的啮合状态,造成传递误差变大。图17是未修改时轴承作用力和修改后轴承作用力的差值曲线,可以看出多数频率下轴承作用力变化不大,在部分频率范围内既有大幅增大,也有大幅减小,这是修改轴后使系统的固有频率移动造成的,总的来说轴承力变化不大。总之,修改轴使第一级齿轮副传递误差增大,但轴承力变化不大,提高了通过齿轮修型减小轴承力的空间。
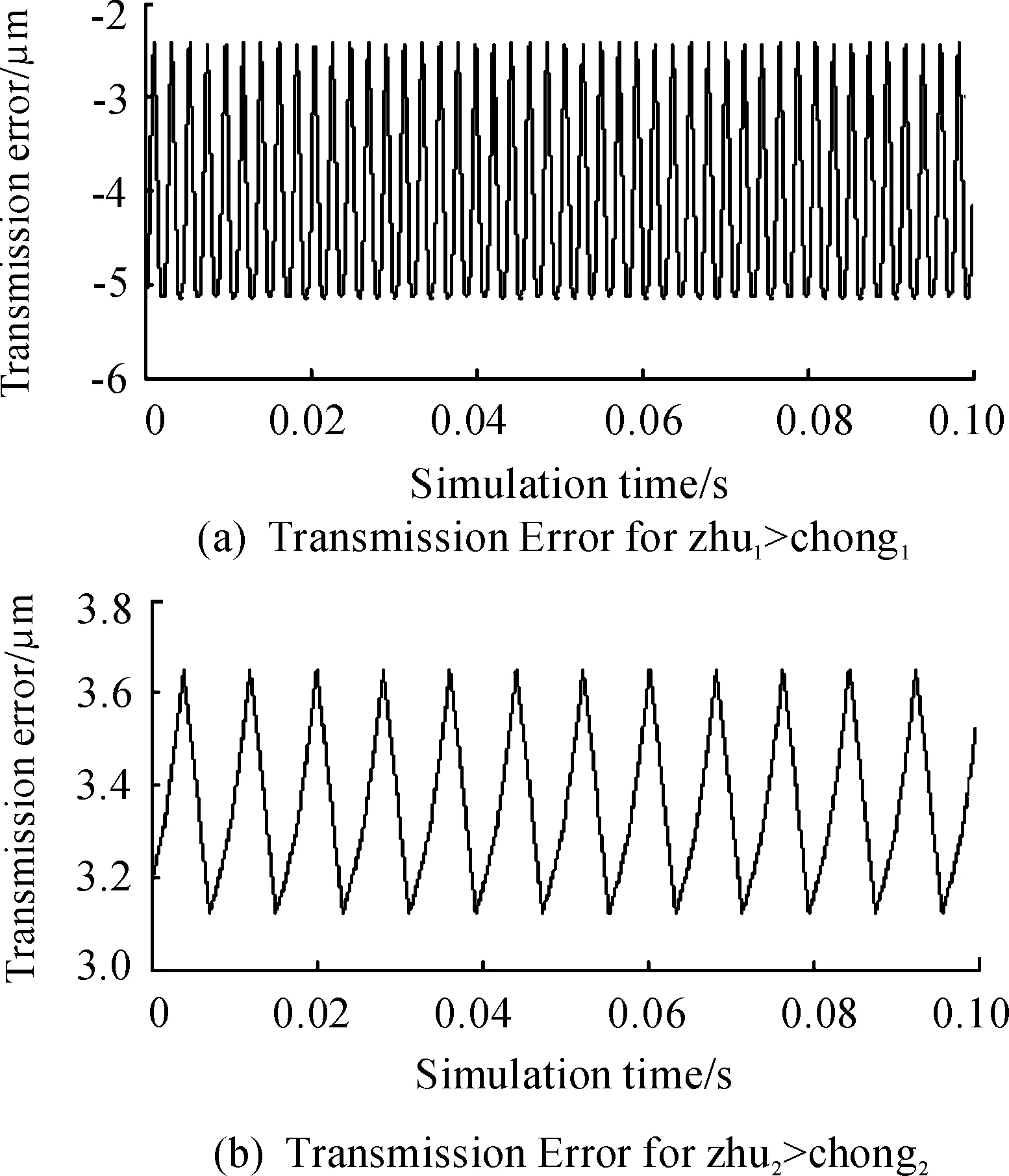
图16 传动误差曲线

图17 轴承作用力差值曲线
5.2 齿面的优化
齿面微观修形是为了减小系统和轮齿变形引起的齿轮错位,尽可能地使齿轮在发生接触受载变形后,齿面压力分布均匀,从而减轻齿面的偏载现象,保证轮齿受载变形后依然能够相对平稳地传递力矩。从Romax齿轮载荷分析结果可以看出,修形前齿轮出现极其严重的偏载现象,低速端不承受载荷,而高速端载荷却很高,因此必须对齿轮进行修形。
Romax软件自带的修形曲线有直线和抛物线,使用时不许手动确定修形曲线的具体形状,只需在软件中确定修形量、修形长度和响应的修形曲线类型。本文只对主动齿轮的啮合面进行齿向修形,修形曲线为直线,第一级主动齿轮啮合面修形量为20 μm、齿向倾度30 μm,第二级主动齿轮啮合面修形量为215 μm、齿向倾度-10 μm。修形后齿轮载荷分布得到很大的改善、传递误差也大大减低、轴承作用力也减小很多,优化结果如图18所示。
5.3 壳体的优化
本研究对壳体进行三处局部优化,一是在箱体轴承座下方加横向加强筋,二是在两侧的螺栓孔间增加一个螺栓孔,用于螺栓固定,三是在盖板的下表面加加强筋。
本研究以5.2中得到的轴承作用力为激励,分别计算优化前和优化后壳体的振动响应,取了三个测试点,分别为箱盖上后端某处(1号测点)、箱体中间轴承座下方某处(2号测点)以及箱体底板面中间点(3号测点)。优化前和优化后壳体对应点的振动加速度差值曲线如图19所示,除了1号测点由于移频是某些频率振动大幅度加强和减弱外,其余两个测点的振动大大减弱,说明壳体的优化效果明显。
5.4 优化后的声辐射预测
采用5.1、5.2和5.3小节中所述的方法即轴-齿形-壳体综合优化方法对减速器进行优化,优化后辐射声功率谱曲线如图20所示,声功率的降低量曲线如图21所示,在大部分频率谱曲线下声功率都大大减低,各峰值降低量分别为34.54 dB、28.12 dB、24.47 dB、13.68 dB、13.17 dB、18.87 dB以及11.48 dB。
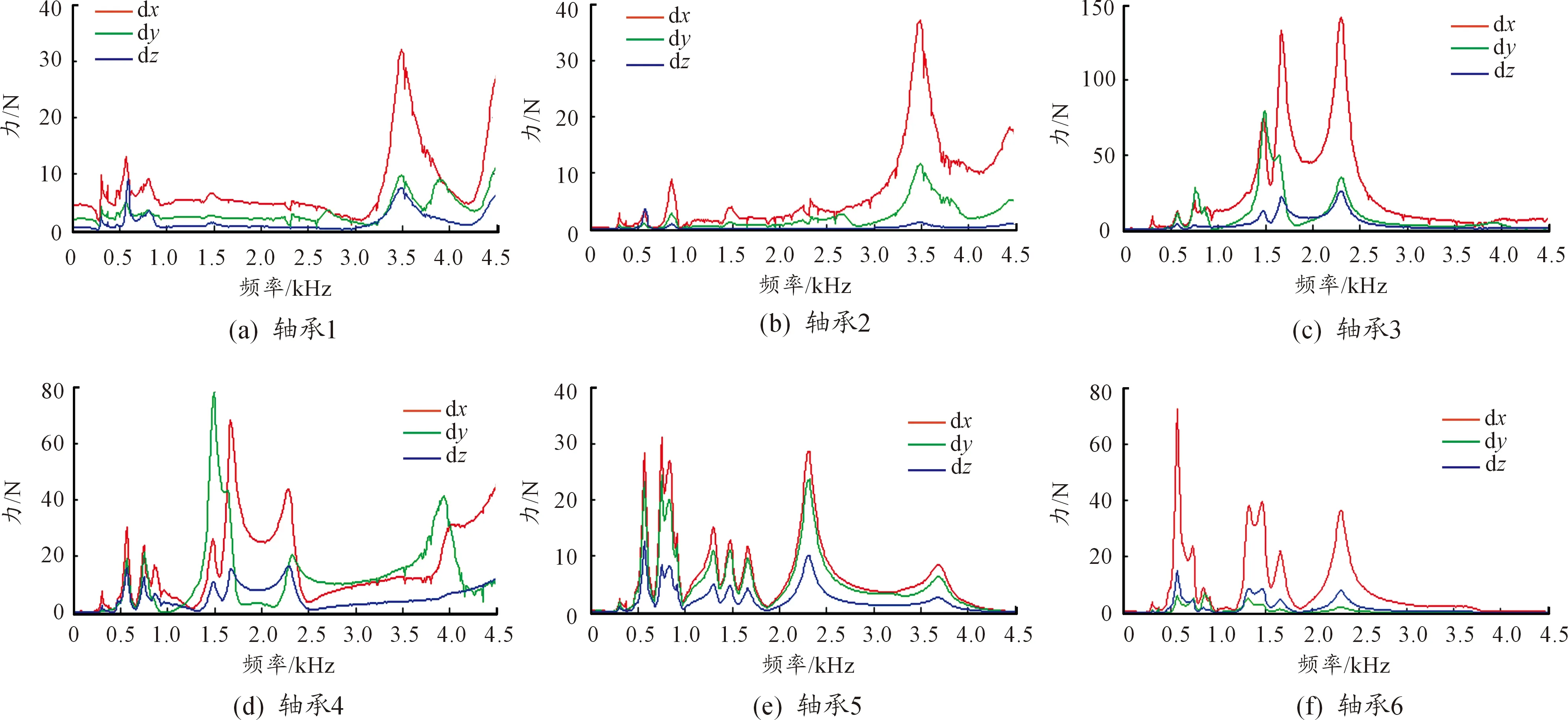
图18 优化后轴承作用力曲线
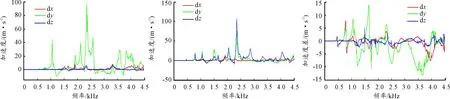
图19 测点加速度差值曲线
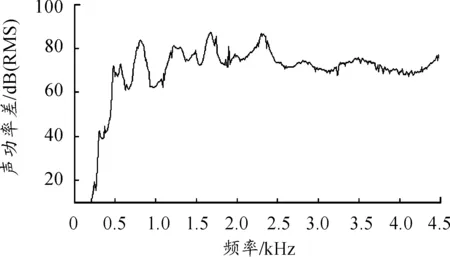
图20 优化后声功率谱曲线
6 结论
1) 齿轮副传动误差激励引起振动,经齿轮、轴以及轴承传递到壳体上,齿轮-转子系统的固有特性对振动的传递影响巨大;
2) 壳体的固有特性对壳体的振动和声辐射影响深远,而固定位置的选择和数量对壳体的固有特性影响非常大;
3) 本文提出的轴-齿面-壳体综合优化方法对降低减速器声辐射、改善其NVH性能具有良好的效果,可成为齿轮传动NVH设计的重要依据。
