一类Monge-Ampère系统非平凡径向凸解的存在性
2019-07-04薛春艳
杨 洋, 薛春艳
(北京信息科技大学 理学院, 北京 100129)
考察如下Monge-Ampère系统:
(1)
在单位球B={x∈RN:x<1}中非平凡径向凸解的存在性。其中,D2ui(i=1,2,…,n)是ui的Hessian矩阵,即
另外,fi(i=1,2,…,n)满足下列条件
H1:fi∈C[R+,R+]且fi(0)=0.其中,R+=[0,+∞)。
当n=2时,Monge-Ampère系统(1)退化为Zhang和Qi在文献[1]中研究的问题。作者运用不动点指数理论证明了该问题解的存在性。与文献[1]相比,本文考虑系统(1)中非线性项为一般函数时的情况,并证明了系统(1)非平凡径向凸解的存在性。
考虑到生产和科技发展的需要,本文主要研究一类完全非线性偏微分方程----Monge-Ampère方程。众所周知,Monge-Ampère方程是在18世纪由2位法国数学家Monge和Ampère建立的。自此之后,Monge-Ampère方程一直是非线性偏微分方程研究中的热点,在流体力学、大气物理学、光学等许多领域中起着非常重要的作用。同时,国内外的学者们将它广泛应用于最优运输、仿射几何等问题中。已取得了很多好的结果[2-5]。
例如,Zhang和Wang在文献[4]中运用移动平面法研究了下列Monge-Ampère方程
解的存在性。其中,Ω是一个有界光滑的严格凸区域。
在文献[5]中,Kutev利用Schauder’s不动点定理证明了下列Monge-Ampère方程
严格凸解的存在性。其中,B={x
在以往文献中,作者大多研究非线性项是幂函数或是指数函数的Monge-Ampère方程。目前为止,对非线性项为一般函数的Monge-Ampère方程的研究并不多见[6],尤其对非线性项为一般函数的Monge-Ampère系统的研究更少[7-8]。本文致力于解决在这种情况下的Monge-Ampère系统非平凡径向凸解的存在性问题,应用的主要工具是不动点指数理论。
1 预备知识
在本节中,主要介绍一些基本概念和引理。
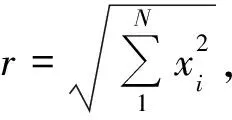
(2)
根据式(2),可将系统(1)化为下列系统
(3)
其中,N≥2,i=1,2,…,n。
令-ui(r)=vi(t),则系统(3)可退化为
(4)
接下来,主要讨论系统(4)正解的存在性。
注:由上面的变换可知,Monge-Ampère系统(1)等价于微分系统(4)。因此,若v=(v1,v2,…,vn)是系统(4)的解,则u=(-v1,-v2,…,-vn)=(u1,u2,…,un)是系统(1)的解;若u=(u1,u2,…,un)是系统(1)的解,则v=(-u1,-u2,…,-un)=(v1,v2,…,vn)是系统(4)的解。
显然,X是实Banach空间。另外,定义X1=C1[0,1]。
为了应用不动点指数理论,在Banach空间X中构造锥K
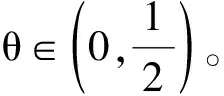
Kr=vi∈X:vi 对任意vi∈K,定义算子Ti:K→X(i=1,2,…,n) 定义T:K→X为复合算子且T=T1T2…Tn-1Tn。由下面的引理2可知,T1,T2,…,Tn-1,Tn,T都全连续。通过计算可得,当(v1,v2,…,vn)∈K{0}×…×K{0}且满足v1=T1v2,v2=T2v3,…,vn=Tnv1时,(v1,v2,…,vn)∈X1×…×X1是系统(4)的解。因此,若v1∈K{0}是T的一个不动点,定义v1=T1v2,v2=T2v3,…,vn=Tnv1,则有v2,…,vn∈K{0},那么(v1,v2,…,vn)∈X1×…×X1是系统(4)的解。反之,若(v1,v2,…,vn)∈X1×…×X1是系统(4)的解,则v1是算子T在锥K上的一个非平凡不动点。因此本文主要任务是找T的一个不动点。 vi(t)≥min{t,1-t}vi,t∈J。 并且,当vi(0)=vi时,有 vi(t)≥(1-t)vi,t∈J。 证明 类似于文献[3]中引理2.2的证明。 引理2 假设条件(H1)成立,则T(K)⊂K且T:K→K是全连续算子。 证明 观察算子的表达式可知,每一个算子都是[0,1]上的非负凹C1-函数。由引理1可知,上述的n个算子是从K映射到K的。运用Arzel-Ascoli定理,可得每一个算子都是全连续算子。因此,复合算子T也是从K映射到K的全连续算子。 为了证明定理1,给出下列引理,见文献[11]。 1) 如果Ax≥x,∀x∈∂Kr那么i(A,Kr,K)=0; 2) 如果Ax≤x,∀x∈∂Kr那么i(A,Kr,K)=1。 在这一节中,运用引理3讨论系统(1)非平凡径向凸解的存在性。 引入记号如下: 定理1 假设条件(H1)成立,则下列结论成立。 1) 若fi0=0且fi∞=∞,则系统(1)至少有一个非平凡径向凸解; 2) 若fi0=∞且fi∞=0,则系统(1)至少有一个非平凡径向凸解。 证明 因为当条件ⅱ)成立时的证明,和条件ⅰ)成立时的证明方法类似,所以仅证明当条件i)成立时结论成立。 如果fi0=0,则存在0<ε<1和0 fi(vi+1)≤ε(vi+1)N,0≤vi+1(t)≤r,∀t∈[0,1] 因此,对任意vi+1∈∂Kr,得 同理可得 则有, 由T算子的定义可知, T(v1)=T1T2…Tn(v1)≤εv1, 意味着 T(v1)≤εv1≤v1,∀v1∈∂Kr。 (5) 另一方面,如果fi∞=∞,则存在η>0和R>r>0使得 fi(vi+1)≥η(vi+1)N,vi+1(t)≥R,∀t∈[0,1] 其中,η满足 ηγNξN(1-ξ)N>1, vi+1(t)≥γvi+1=γο=R,t∈[0,1] 进而,得 同理可得 则可知 由算子定义可知, T(v1)=T1T2…Tn(v1)≥ηγNξN(1-ξ)Nv1, 意味着 T(v1)≥ηγNξN(1-ξ)Nv1≥v1,∀v1∈∂KR。 (6) 由式子(5)和(6),根据引理3可知 i(T,KR,K)=0,i(T,Kr,K)=1。 由不动点指数的可加性,得 (7) 综上所述,本文利用不动点指数理论研究一类Monge-Ampère系统,并证明了非线性项为一般函数的Monge-Ampère系统非平凡径向凸解的存在性。 主要从2个方面推广了Zhang和Qi在文献[1]中研究的问题: 1) 由两个方程的Monge-Ampère方程组推广到n个方程的Monge-Ampère系统。 2) 将f1,f2为幂函数推广到f1,f2,…,fn为一般函数。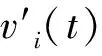
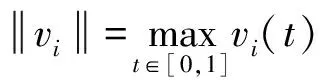
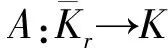
2 主要结果
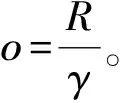
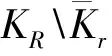
3 结 语
