基于增量型极限学习机的材料力学性能预测

吴 迪, 曹培智, 张国英, 焦兴强

(沈阳师范大学 物理科学与技术学院, 沈阳 110034)

0 引 言

传统的材料科学研究和材料制备过程大都依赖于大量实验,这个过程中需要投入大量的时间、人力、物质资源,尤其研究成本较高。专家系统可以利用领域内已有的专家经验进行推理并做出决策,提高了研究效率,但材料中依然存在一些较为复杂的内在规律很难用明确的数学模型描述,因此在一些材料研究中专家系统也不能解决所有现有问题。

近年来计算机仿真在材料科学的研究中发挥了巨大的作用,计算材料学的发展为材料科学的研究提供了新的方法,常用的计算材料学方法有有限元方法、第一原理法、人工神经网络等。对于一些结构复杂很难描述其表达函数的材料结构,神经网络直接对实验数据进行迭代训练来得到反应数据内在规律的模型,因此对复杂的非线性系统有很好的映射能力,人工神经网络在材料制备、结构分析、性能分析中有很多应用。刘贵立等[1]利用BP神经网络对高Co-Ni二次硬化钢进行结构分析和力学性能预测。但BP神经网络需要重复迭代训练,速度较慢,可能陷入局部极小值,又有学习率不确定的问题。极限学习机(extreme learning machine,ELM)相较于BP神经网络,通过设置隐层节点数,随机赋予网络输入权值和阈值,在算法过程中只需计算隐层输出权值,有训练速度快、泛化程度高、训练参数少的优点[2]。针对普通的极限学习机隐层节的最佳选择问题,本文采用增量型极限学习机[3](incremental extreme learning machine,I-ELM)对高Co-Ni二次硬化钢进行研究。I-ELM会逐渐向网络中添加节点,然后计算网络输出误差,直到达到满足误差要求或到达最大节点数时算法结束,既能满足训练速度快、拟合程度高的条件,又可以避免ELM节点选取不当导致的算法不稳定问题。

1 实验数据处理

高Co-Ni二次硬化钢样本数据取自文献[1]共41组见表1,合金元素C、Ni、Co、Cr、Mo、Nb、Ti和时效温度、淬火温度为9项输入指标分别用I1～I9表示;屈服强度E0.2(MPa)、抗拉强度Eb(MPa)、韧性Kic(MPam1/2)、延伸率(W)、截面收缩率(ψ)为5项输出指标,分别用O1～O5表示。将其划分为33组训练集,8组测试集见表2。

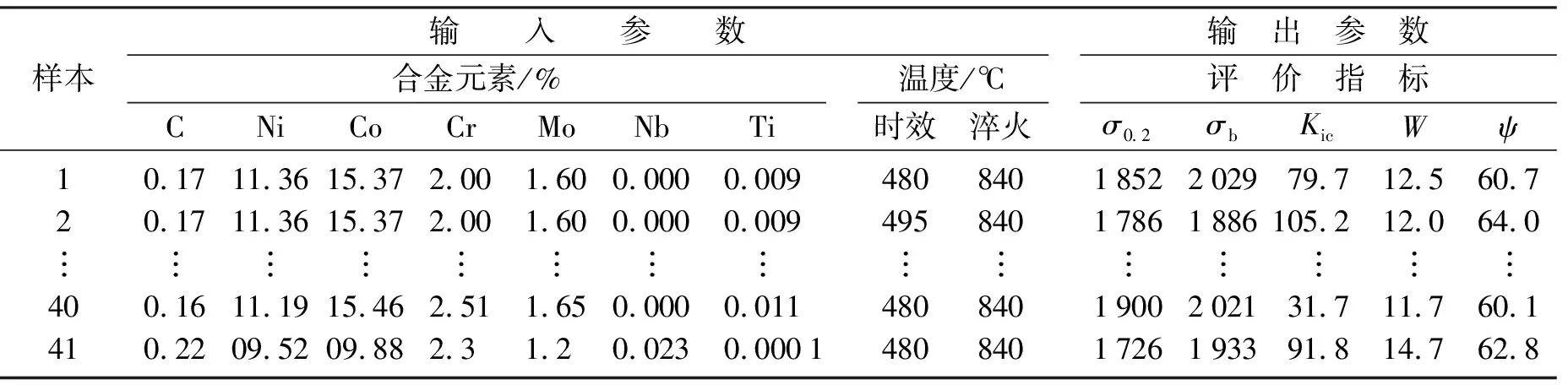
表1 高Co-Ni二次硬化钢部分样本数据Table 1 The partial sample data of high Co-Ni secondary hardened steel

表2 高Co-Ni二次硬化钢数据集划分

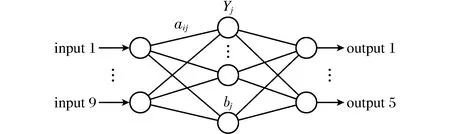
图1 SLFN网络结构图Fig.1 The SLFN network structure

实验数据经过归一化使值域在区间[0,1]内,令一组数据中最大值为a,最小值为b,则归一化前数据X对应归一化后为

c=(X-b)/(a-b)

(1)

同理,网络输出的数据c经过反归一化后是实际物理数据:

X=a+c×(b-a)

(2)

2 高Co-Ni二次硬化钢BP神经网络模型

BP神经网络是一种误差反向传播结构如图1所示,在其网络结构中有20个隐层神经元,9个输入层神经元,5个输出层神经元。

aij表示第i个输入层神经元到第j个隐层神经元连接权值,取值范围是[-1,1];bL表示第L个隐层神经元的阈值,取值范围是[-1,1]。参考文献[1]中的网络指标函数E为

(3)

其中:Dij表示训练模拟输出值;Oij表示对应的实际数据;P为样本数。设置BP网络训练的最大循环次数为1 000次,期望误差指标E小于0.001。

3 高Co-Ni二次硬化钢I-ELM模型

3.1I-ELM

增量型极限学习机(I-ELM)也是一种单隐层前向传播神经网络[6], 其网络结构同图1所示。 I-ELM网络结构为m个输入神经元,n个输出神经元,L个隐层神经元。 训练样本为X=[x1,x2,…,xm],X的维数为m×N;Y=[y1,y2,…,yn],Y的维数为N×n。 假设网络隐层神经元个数最大值为N, 网络余差为E(指网络输出与实际数据间的差值矩阵), 期望误差为ε。 则I-ELM训练过程[4]如下:

1) 首先给隐层神经元与输入节点的连接权值a和阈值b设定一个随机值。

2) 计算当前加法隐层神经元输入x公式为:

x=aX+b

(4)

3) 计算当前加法隐层神经元输出:

(5)

4) 由最小二乘法计算该隐层神经元输出权值矩阵:

(6)

5) 计算增加一个隐层神经元后网络的余差:

E′=E-βH

(7)

6) 判断是否超过最大节点数L>N或误差指标是否满足要求E<ε,若是则算法结束,否则令L=L+1,返回1)继续循环。

文献[3]中的Theorem Ⅱ.1证明了随着隐层节点添加,由式(6)最小二乘法计算出的权值可以使网络误差逐渐下降。

I-ELM训练速度快的优点对材料数学模型进行在线预测有很多的潜在作用[12]。

3.2 仿真研究

本文对高Co-Ni二次硬化钢进行了I-ELM模型和BP神经网络模型的研究,并将其结果进行对比,2种方法均在同一计算机的Matlab 2018a版本上完成。

I-ELM模型初始化参数设置:隐层节点最大值3 000,初始隐层节点数N=0,初始误差矩阵E为测试集输出矩阵,网络精度ε为误差矩阵E的二范数,即矩阵ETE的最大特征值开平方。设定期望精度ε不高于1.5。表1为高Co-Ni二次硬化钢数据集的划分。

图2为I-ELM网络对测试集数据的预测结果与材料实际数据的对比,结果表明拟合效果良好。图2中有5组数据,每一组有2条的数据线,其中红线表示I-ELM模型预测输出的数据值,蓝线表示实际数据值。为了便于观察对数据绘图时进行了放缩操作,图中数据与真实值比例对应关系参照表3。

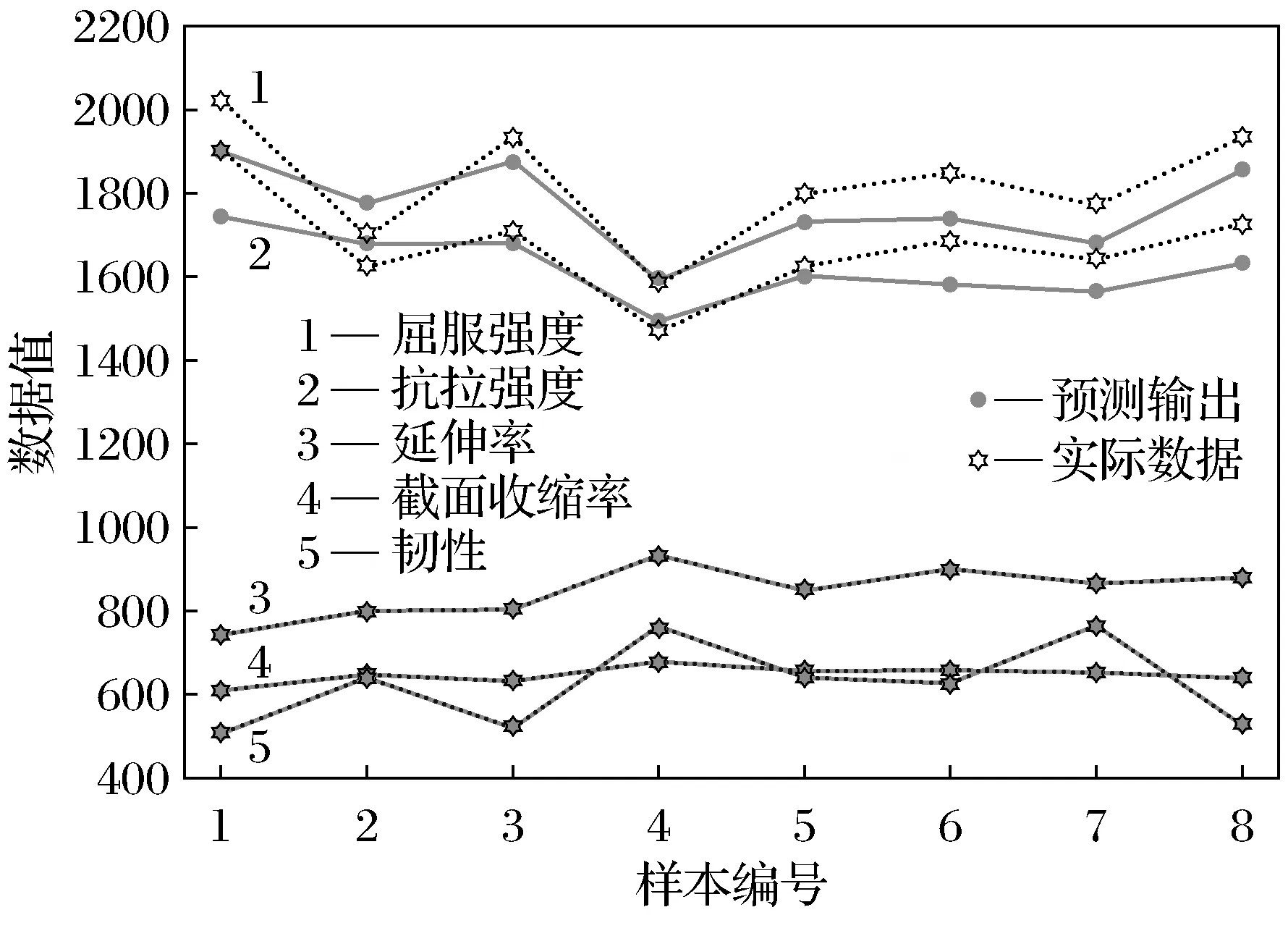
图2 5组I-ELM模型预测结果Fig.2 Five groups prediction results of I-ELM model

表3 绘图数据值与真实值对应比例Table 3 The corresponding ratio of plot data values to real values

3.3 I-ELM预测微量元素Co时效温度对材料力学性能影响

以表1中样本40数据为基础,通过控制变量分别改变微量元素Co含量和时效温度,研究微量元素Co和时效温度对材料力学性能的影响。计算结果如图3和图4所示。为便于观察,图中显示韧性,截面收缩率指标为实际值10倍,延伸率为实际值100倍。当微量元素Co含量由8%逐渐增加时,材料的屈服强度、抗拉强度逐渐增加,而延伸率和韧性会降低;当时效温度由480 ℃逐渐增加,材料的屈服强度、抗拉强度会降低,延伸率和韧性增加。截面收缩率受微量元素Co和时效温度变化影响较小。

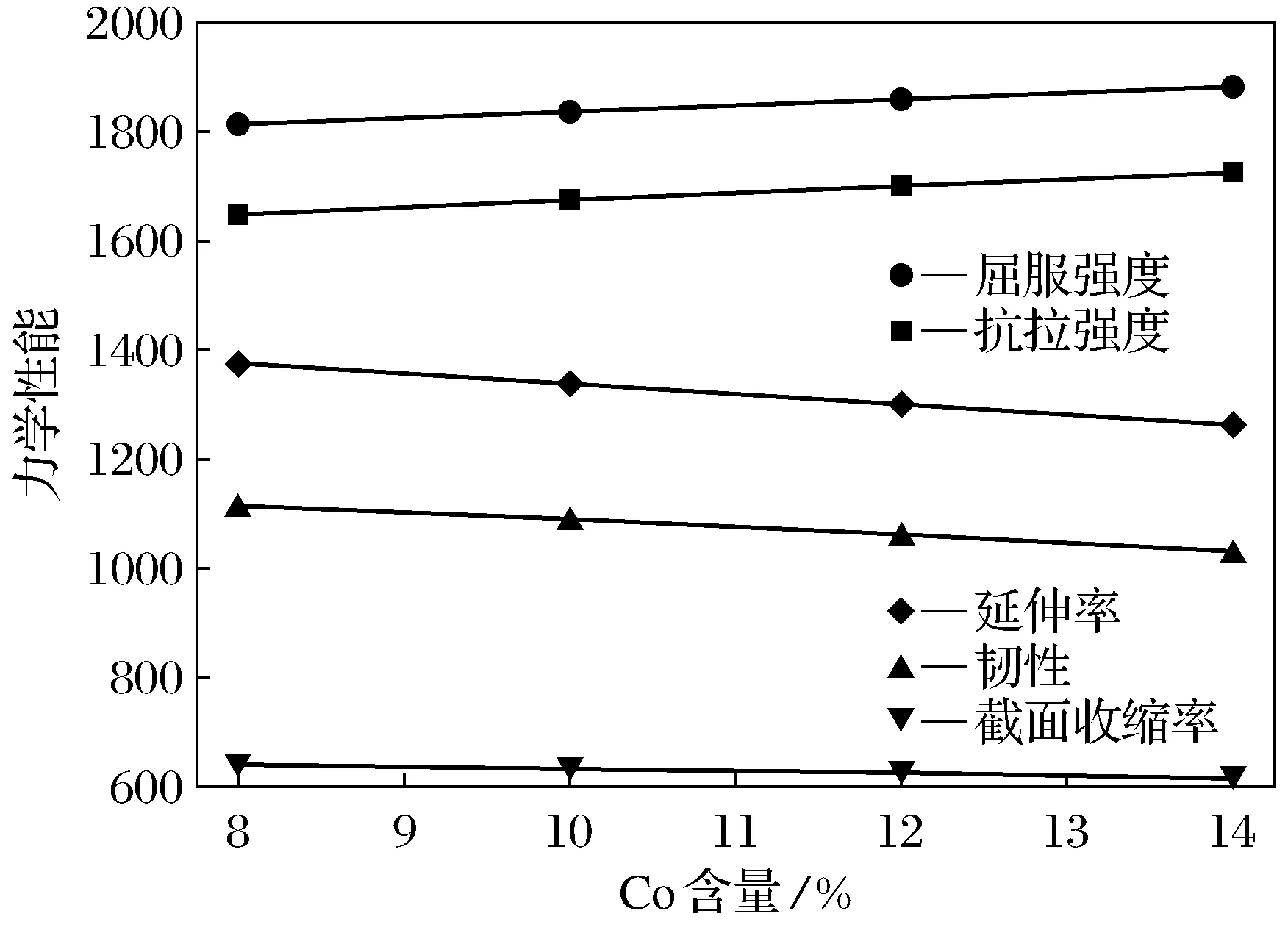
图3 Co元素对材料力学性能影响Fig.3 The effect of Co element on mechanical materials

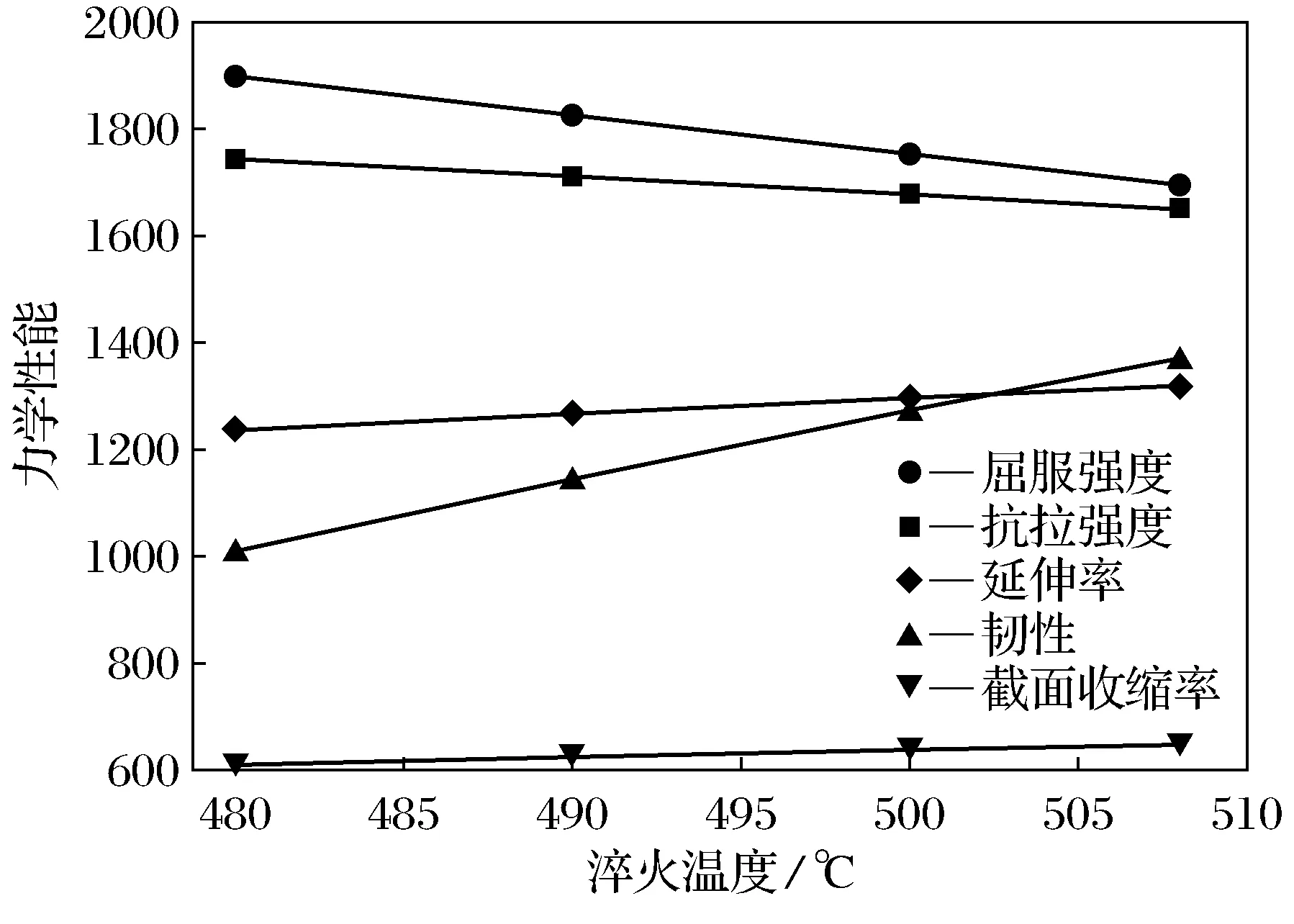
图4 时效温度对材料力学性能影响

理论分析:根据文献[10]研究,材料中Co元素的加入使得铁短程有序,降低了铁自扩散系数;元素Co还是一种固溶强化元素,能削减残余奥氏体量,致使的强度性能降低,增添了马氏体量。但铁中Co元素含量不应过多,过多会使韧性下降,I-ELM预测结果与文献[10]结果相符。文献[11]指出随着时效温度的提高,强度会下降,韧性会提高;时效温度对延伸率及截面收缩率影响较小,这与I-ELM网络的预测结果相符。

4 I-ELM模型与BP神经网络模型的拟合效果对比

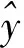
(8)

表4表示I-ELM和BP神经网络对高Co-Ni二次硬化钢数据训练结束后模型预测结果的决定系数对比。5项评价指标中,对材料的拟合程度I-ELM均优于BP神经网络,其中韧性指标由于1号和3号样本存在离群点导致拟合精度较低。

表4 决定系数R2对比结果Table 4 The determination coefficient comparison results

还可以通过如下几项指标来衡量I-ELM和BP神经网络对高Co-Ni二次硬化钢的训练效果,其结果列在表5中。

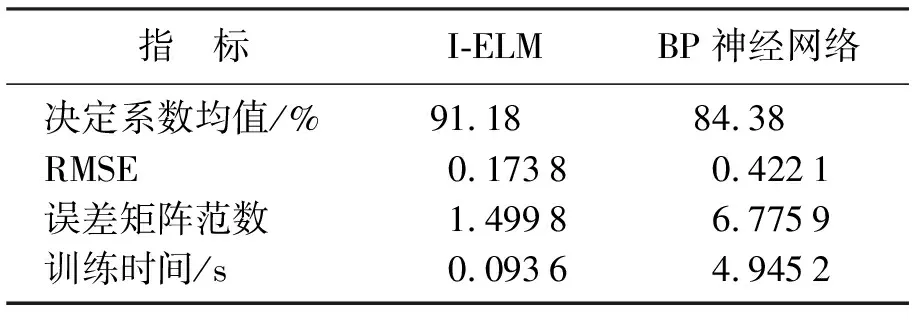
表5 I-ELM和BP神经网络各项性能对比

1) 决定系数均值是5组决定系数R2的平均值,反映网络预测模型的拟合效果。

2) 均方根误差(RMSE)是指观察值与真实值偏差的平方和观测次数n比值的平方根,本次试验中反映预测值和实际值的关系,是预测值与真实值的误差的平方的算术平均值再开方。RMSE反映了预测数据偏离真实值的程度,RMSE越小,表示模型预测精度越高。

(9)

3) 误差矩阵的2范数(E2)是指即误差矩阵ETE矩阵的最大特征值的开平方,此次实验中用来表征模型训练精度。

4) 训练时间(s)反映网络对数据训练的速度快慢。

5 结 论

本文采用I-ELM训练高Co-Ni二次硬化钢材料模型,同BP神经网络相比,直接计算隐层神经元输出权值矩阵可极大地减少计算量,然后通过增加隐层节点的方式调整网络结构,防止出现过拟合问题。结果表明,I-ELM对样本数量少、材料结构复杂的高Co-Ni二次硬化钢材料拟合效果很好。模型预测的结果能较好地反映材料力学性能规律。下一步I-ELM网络模型还可以通过对隐层输出增加偏置从而提高部分神经元输出权值,提高网络模型的结构效率。综上,本文为高Co-Ni二次硬化钢材料力学性能研究提供了一种在样本数量少条件下采用现代优化算法进行快速高精度拟合的有益参考。