一类具有优化控制策略的计算机病毒传播模型分析

2019-07-04谭宏武白云霄乔蓉蓉

陕西科技大学学报 2019年4期

谭宏武，白云霄，乔蓉蓉

(陕西科技大学文理学院，陕西西安 710021)

0 引言

2017年5月，一种名为“想哭”的勒索病毒席卷全球，在短短一周的时间里，上百个国家和地区受到影响.据美国有线新闻网报道，截至2017年5月15日，大约有150个国家受到影响，至少30万台电脑被病毒感染[1].可见，计算病毒对信息安全的危害，以及带来的相应的经济损失不可估量.因此，计算机病毒的防治就成为信息安全领域内重要的研究课题之一[2,3].

计算机病毒是指编制或者在计算机中插入的破坏计算机功能或者毁坏数据，影响计算机使用，并能自我复制的一组计算机指令或者程序代码[4].它具有传播性、隐蔽性、感染性、潜伏性、可激发性、表现性或破坏性等特点[5].与生物病毒相似，计算机病毒不仅会感染其它文件，而且自身也会不断复制.计算机病毒的传染渠道多种多样，它可能会通过互联网，感染网络另一端的一台或多台计算机，也可能通过U盘等其它移动设备进行传播.

目前，基于计算机病毒传播机理的动力学模型分析已经不少[6-12].但是在计算机病毒传播的动力学模型中考虑优化控制的研究很少.本文考虑一类具有一定安全防范控制措施的计算机病毒传播模型.通过定性的动力学理论和优化控制理论，来设计可行、有效的控制计算机病毒传播的措施方案，并利用数值模拟展示措施的有效性.

1 计算机病毒传播的模型

基于文献[11]的研究内容，可将所有联网和未联网的计算机看作网络中的节点，根据节点所处的状态，即，是否感染病毒，将所有节点分为三类，分别是易感类、潜伏感染类和病毒爆发类，并且分别用S(t)、L(t)和B(t)表示t时刻这三类的个体数量.设N(t)=S(t)+L(t)+B(t)，表示t时刻网络中的总节点数.

假设一台计算机一旦接入互联网，则必为这三类中的某一类，且这三类节点分别以固定概率接入互联网，即易感类S(t)的接入概率为μ1，潜伏感染类L(t)的接入概率为μ2，病毒爆发类B(t)的接入概率为μ3.网络中的节点会以相同的概率δ断开与网络的连接.每个易感类节点被可移动存储设备感染的概率为θ.在t时刻，每一个易感类节点被潜伏感染类节点L感染病毒的概率为β1L，被病毒爆发类节点B感染病毒的概率为β2B，其中β1和β2均为常数.潜伏感染类节点以概率α爆发成为病毒爆发类节点.潜伏感染类节点通过修复和杀毒的方式恢复为易感类节点的概率为γ1，病毒爆发类节点通过修复和杀毒的方式恢复为易感类的概率为γ2.根据以上假设，本文建立了下面的计算机病毒传播模型：

(1)

显然，模型(1)中所有的参数都是正数，并且模型(1)任意一个具有非负初值的解都是非负的.对于模型(1)的有界性有下面的结论：

证明：由于N(t)=S(t)+L(t)+B(t)，可以得到下面的方程：

证毕.

(2)

2 平衡点的存在性和稳定性

定理1模型(2)存在唯一的计算机病毒平衡点E*=(L*,B*)，其中

这里

证明：为了得到模型(2)的计算机病毒平衡点，需要求解下面的方程：

(3)

由方程组(3)中的第二个方程，可得

XL2+YL+Z=0，

(4)

其中，

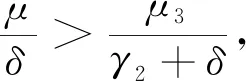
证毕.

定理2模型(2)的计算机病毒平衡点E*=(L*,B*)是局部渐近稳定的.

证明：由定理1可知模型(2)存在唯一的计算机病毒平衡点E*=(L*,B*).将系统(2)在平衡点E*处线性化，可得Jacobian矩阵为：

(γ1+α+δ),

其特征方程为λ2+a1λ+a0=0，其中

a1=β1(2L*+B*)+β2B*+α+γ1+γ2+θ+

2δ-β1N*，

a0=[β1(2L*+B*)+β2B*+α+δ+γ1+θ-

β1N*]·(γ2+δ)+α[β2(L*+2B*)+β1L*+

θ-β2N].

由于

μ2+β1S*L*+β2S*B*-(α+γ1+δ)L*+θS*=0,

L*[β1S*-(α+γ1+δ)]+μ2+β2S*B*+θS*=0.

这说明β1S*-(α+γ1+δ)<0成立，也就是

a1=β1(2L*+B*)+β2B*+α+γ1+γ2+θ+

2δ-β1N*=β1L*+β2B*-β1S*+α+γ1+

α+γ1+γ2+θ+2δ=β1L*+β2B*+γ2+

θ+δ>0.

另外，由于

μ2+β1S*L*+β2S*B*-(α+γ1+δ)L*+θS*=0,

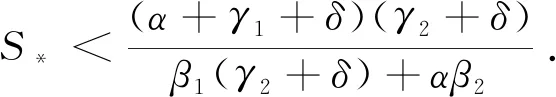
a0=[β1(2L*+B*)+β2B*+α+δ+γ1+

θ-β1N*]·(γ2+δ)+α[β2(L*+2B*)+

β1L*+θ-β2N*]=[β1(2L*+B*)+β2B*+

α+δ+γ1+θ](γ2+δ)+α[β2(L*+2B*)+

β1L*+θ]-[β1(γ2+δ)+αβ2]N*=(α+

γ1+δ)(γ2+δ)+(β1L*+β2B*+θ)·(α+

γ2+δ)-[β1(γ2+δ)+αβ2]S*>(β1L*+

β2B*+θ)(α+γ2+δ)>0.

由根与系数的关系以及霍尔维兹判据[15,16]可知，特征方程的两个根的实部都小于零.因此，地方病平衡点E*=(L*,B*)是局部渐近稳定的.

证毕.

接下来，证明模型(2)的计算机病毒平衡点E*是全局渐近稳定性的.为此，给出以下引理.

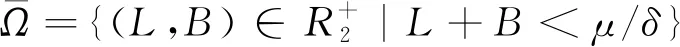
直接计算可得：

由Bendixson-Dulac定理[17]可知，引理2成立.

证毕.

定理3模型(2)的计算机病毒平衡点E*是全局渐近稳定的.

证明：由引理1可知系统(1)有界，这说明系统(2)也有有界的.定理1说明系统(2)存在唯一的计算机病毒平衡点E*.定理2说明系统(2)唯一的计算机病毒平衡点E*是局部渐近稳定的，引理2显示系统(2)在可行域内部不存在周期轨.

结合广义的Poincaré-Bendixson定理[17]，及以上分析，可知计算机病毒平衡点E*是全局渐近稳定的.

证毕.

由于模型(2)和模型(1)有相同的动力学性态，也就是模型(1)也存在唯一的计算机病毒平衡点

3 控制措施

在本节中，将利用庞特里亚金极大值原理[18-20]来分析在计算机运行的过程中采取定期查毒、杀毒、升级杀毒软件、使用移动设备前首先进行查杀毒等措施对于减少计算机感染病毒的有效性.基于模型(1)，给出下面的具有优化控制措施的计算机病毒传播模型：

(5)

这里，u1(t)表示对计算机进行定期的查毒杀毒，并且对计算机中的杀毒软件进行更新升级等方式降低计算机病毒的传播.这一控制措施有助于及时发现网络中的计算机病毒，并在最短的时间进行杀毒处理.如果发现病毒不能及时处理，就采取断网的方式强行将计算机病毒的传播在网络中终止.u2(t)表示对接入计算机前的移动设备进行病毒检查的控制措施.这一措施可以有效地降低由于插入感染的移动设备而导致健康计算机的感染.可给出控制域为：

U={(u1,u2)∈L1(t0,tf)0≤ui≤1,i=1,2}

定义目标函数：

J(u1(t),u2(t))=

(6)

为了寻找最优解，定义Hamilton方程为：

λ1[μ1-u1(t)β1L(t)S(t)-u1(t)β2B(t)S(t)+

γ1L(t)+γ2B(t)-(δ+u2(t)θ)S(t)]+

λ2[μ2+u1(t)β1L(t)S(t)+u1(t)β2B(t)S(t)-

(γ1+α+δ)L(t)+u2(t)θS(t)]+

λ3[μ3+αL(t)-(γ2+δ)B(t)]

(7)

其中λi(i=1,2,3)为伴随变量，满足方程：

(8)

横截条件为λi(tf)=0(i=1,2,3).利用最优控制条件，可得

(9)

(10)

由于0≤ui≤1,i=1,2,利用控制域U，有以下三种情况出现：

因此有：

(11)

类似地，有：

(12)

4 数值模拟与讨论

在这部分，将借助数学软件Matlab来数值展示系统(5)的动力学行为，以及各类控制措施对于计算机病毒传播的作用.

首先展示系统(1)的计算机病毒平衡点是全局渐近稳定的.为此，选取β1=0.01，β2=0.05，γ1=0.3，γ2=0.1，μ1=4，μ2=2，μ3=3，α=0.2，δ=0.1，以及θ=0.2.相应地，可以得到计算机病毒平衡点为(S*,L*,B*)=(6.185 0,34.407 5,49.649 7).数值模拟显示，模型(1)在五组不同初值下的解都会随着时间的变化而趋近于计算机病毒平衡点，如图1所示.这说明计算机病毒平衡点是全局渐近稳定的.也就是，在不采取控制措施的情况下，计算机病毒将会在整个网络中永久存在.