轨道-路基体系一致动力相似设计方法与动力试验
2019-07-04周颖,陈瑾,2
周 颖, 陈 瑾,2
(1. 同济大学 土木工程防灾国家重点实验室, 上海 200092; 2. 长安大学 建筑工程学院, 陕西 西安 710061)
截至2017年底,全国高速铁路营业里程达到了2.5万公里,占世界高铁总量的66.3%.根据规划,到2020年,中国高速铁路营业里程将达到3万公里,高速铁路网覆盖80%以上的大城市.高速铁路的快速发展给许多国家带来了巨大的社会和经济效益,但同时在其自身也呈现出了一些问题,特别是长期高速运营下轨道结构的离缝问题,以及极端环境下路基结构的翻浆和变形问题等[1-3].
在高速列车荷载下,轨道结构和路基结构是一个共同工作的整体体系,轨道结构将上部动荷载向下传递给路基,路基产生的沉降变形在动荷载作用下又会对轨道结构形成不良效应,这种轨道结构和路基结构之间的耦合作用是典型的土和结构相互作用问题.因此,不管是针对轨道结构还是路基结构动力响应试验,在轨道-路基体系这个系统内进行分析研究是相对更为合适的选择.
邹春华等[4-5]在室内建设了1∶1足尺有砟轨道模型,研究结果表明对于定波长的余弦型路基沉降,轨道结构的沉降类别可采取余弦函数来确定,并提出了轨枕临界空吊的计算方法.边学成等[6]室内建立了1∶1的足尺单线无砟轨道路基试验平台,该模型以沪宁城际高速铁路的设计为依据,钢轨、轨道板、路基等均为真实原型材料,该平台实施了多组轨道-路基试验并研究了不同速度和不同环境条件下轨道和路基的振动和动应力响应.王启云等[7]进行了无砟轨道路基结构1∶1足尺试验模型设计,给出了轴重和速度变参数下的输入荷载的时程曲线.邱明明等[8-9]建立了膨胀土有砟轨道路基系统动力模型试验平台,比较了列车荷载与极端使用环境耦合作用下的新型路堑结构的动力特性,提出一种改进的经验公式来预测膨胀土有碴轨道路基的动应力.冷伍明等[10]以朔黄铁路为原型,开展了重载铁路路基1:1足尺模型的试验研究,结果发现轴重荷载越大,土压力在路基中衰减越慢.王贺等[11]以青荣城际铁路为原型,建立了高速铁路加筋土挡墙模型,得到了挡墙在静、动力激振力下的应力分布规律,结果发现,各向土压力的分布沿拉筋方向呈中间大两端小的特征.
王明昃等[12]在足尺轨道路基试验台上进行了CRTS系列轨道结构系统动力性能的落锤试验研究,通过试验比较了不同轨道结构的振动特性并得到了各轨道系统的动刚度和阻尼系数.詹永祥等[13]进行了1:12桩板结构路基试验,路基和地基采用现场取土制作,采用与原型同标号的微粒混凝土制作桩和上部承载板,分析了不同位置激振时桩板结构路基的动力和变形特性.姜领发等[14]开展了1:2的高铁路基激振模型试验研究,基床和路堤采用现场填料进行填筑,地基部分采用红粘土进行填筑,得到了路基不同位置的动应力和速度的时程变化曲线及衰减特征.Shaer等[15]设计了1∶3的有砟轨道路基模型,轨枕尺寸和土层厚度缩尺为原型的1/3,基床采用未处理的砾石,道砟采用压实的微粒碎石,得到了路基的累积沉降和轨枕加速度的关系.
目前国内外对于动力荷载作用下轨下结构(轨道、路基、地基、桩等)缩尺模型试验设计,多数进行静力相似设计,时间的影响在试验设计当中有待考虑.在实际情况下,轨道和路基结构主要承受的是上部列车荷载动力作用.现有文献表明,随着速度的增加,传导至轨道结构表面的列车动荷载存在放大效应[16],速度越快,动荷载数值越大,轨道和路基结构的动力响应越明显,也就是说轨道和路基结构经历的动力过程与时间相关性大.因此,对于主要承受动力作用并需要考虑时间因素相关性的结构,对其进行考虑时间因素的动力相似设计十分必要.对于路基填料的缩尺,常采用尺寸小些的材料,其与原型的对应关系有待明确.对于采用原型或稍小尺寸材料的缩尺路基,因此在动力相似设计中,应合理选择能动力控制参数来进行路基模型的相似设计[17-20].对于轨道和路基结构两个相互影响的组合体系,缺乏相关相似设计方法考虑组合体系的一致作用.对于这种轨道结构和路基结构之间的耦合作用,应考虑体系的一致作用问题.
针对以上问题,本文提出了一种基于轨道-路基体系一致动力相似设计方法,来实现模拟轨道-路基原型的相互作用、轨道-路基体系中的动力荷载传递、轨道受力特性以及路基沉降变形等的研究.通过不同激振频率下的动力试验,得到不同频率动荷载下路基结构各位置处的加速度分布和衰减特性,以及路基结构各位置处的加速度和激振频率之间的联系,从而探究共振发生的机制.
1 基于轨道-路基体系的组合控制动力相似设计方法
1.1 方法的提出
首先对无砟轨道和路基结构的相似设计进行了如下分析:无砟轨道结构主要由钢筋和混凝土组成,类似于建筑结构中的叠合板,包括预制和现浇部分.对于此结构,基于多年动力试验设计研究基础[21-23],在考虑施工条件和试验能力确定长度相似比Sl后,提出将整体轨道-路基结构体系加速度相似常数Sa定为1来避免重力失真,从而不再附加配重,再通过选用质量密度等可控相似常数,把握构件层次上的内力相似原则,对轨道结构进行动力相似设计.
路基结构是由基床表层、底层和路堤构成的层状体系,组成材料有级配碎石、A、B、C组填料.其主要由散粒体材料组成,材料具有较强的非线性特征,相似设计依据较难选择.周燕国[17]通过动三轴试验和离心机试验发现利用剪切波速可以较合理地表征土体状态和动力变化过程,从而可以为揭示土体场地液化、大变形等动力机理提供定量参数.陈国兴等[19-20]根据时间相似常数和反映重力相似律的Froude值一致[24-25]确定了软土和可液化土地基的长度相似比,通过剪切波速相似建立了模型与原型土的对应关系,获取了有效的试验数据.Froude值一致即量纲相似中的速度相似,可通过量纲协调求出.
因此,本文提出在考虑路基结构与轨道结构一致长度相似比的前提下,控制路基模型剪切波速相似进行路基结构动力设计.轨道-路基体系一致动力相似设计方法,设计基本原则如下:
(1) 轨道结构设计采用结构动力相似设计方法;
(2) 不允许重力失真,即不附加配重,轨道-路基体系加速度相似比Sa为1;
(3) 路基和轨道结构遵循相同的长度相似比Sl;
(4) 通过模型路基与原型路基各层材料(基床表层、基床底层、路堤、地基)的剪切波速相似关系来定义模型材料的长度相似比Sl;
(5) 必须考虑施工条件和试验能力.
根据以上原则和轨道-路基结构体系的特点,选取长度、密度和加速度作为轨道结构的三个可控相似参数,根据似量纲分析法[23],求出包括应力相似常数、速度相似常数在内其余相似常数(式(1)和式(2)),确定路基各层材料的剪切波速的取值(式(3)),再进行相应配置路基和各层材料.
(1)
式中:Sσ为应力相似常数;Sρ为密度相似常数;Sa为加速度相似常数;Sl为长度相似常数.
(2)
(3)
式中:Sv为速度相似常数;Vsm为模型路基各层材料的剪切波速;Vsp为原型路基各层材料的剪切波速.
1.2 模型相似设计
综合考虑模型箱的尺寸、作动器的性能参数、试验室施工条件等因素,本试验轨道-路基结构模型长度相似常数Sl为0.25,密度相似常数Sρ为1,加速度相似常数Sa为1.通过似量纲分析法[23]求得本试验轨道结构模型相似比,见表1.表中,S为相对应物理量的相似常数.
对于轨道模型这种钢筋混凝土结构,动力设计基本原则是把握构件层面上的相似原则[23].轨道板和支承层为正截面受弯构件,控制因素为正截面承载能力,故依据抗弯能力等效的原则进行配筋相似.原型结构、模型结构的弯矩分别表示式(4)和式(5),根据弯矩相似常数(式(6))进行计算得到了模型结构的配筋相似常数(式(7))并进一步得到配筋面积等参数,见表2.
(4)
(5)
(6)
(7)
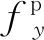
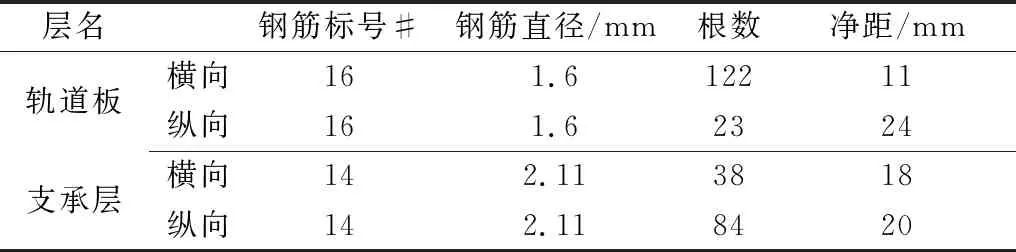
表2 轨道结构配筋
屈畅姿等[26-30]通过现场试验测得了路基原型结构各层的剪切波速范围,在式(2)中取剪切波速相似常数Sv为0.5,从而可以得到各层填料应符合剪切波速的范围,详见表3.
通过参考不同种类土的剪切波速,经多次尝试,最终确定了符合上述波速范围的模型材料.基床表层采用青石子掺5%的水泥,模型基床底层和路堤采用不同压实度相同配比的配置土(中砂、高岭土和水按质量比87∶13∶12.5混合),模型地基采用上海深层软土.模型基床底层、路堤、地基土剪切波速的测试采用了英国GDS共振柱设备[31](图1),结果见表3.由于青石水泥大颗粒成分较多,该设备无法支持,因此,对模型基床表层剪切波速的测试采用在试样现场测试的手段,即在配好的试样中,选择两个同一深度且水平间距不小于0.53 m的位置分别布设加速度传感器,在一端进行敲击,同时采集相应数据结果(采集设备采样频率为500 Hz),水平间距除以两传感器时程曲线峰值点的时间差值得到的速度即为模型基床表层的剪切波速,测试结果见表3.
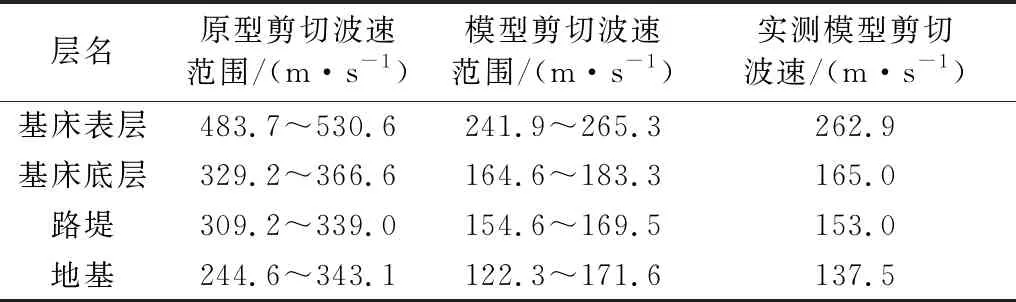
表3 路基各层及地基的剪切波速

图1 弯曲元试验
2 轨道-路基模型体系动力试验
2.1 模型制作
本试验模型位于双线高铁轨道路基模型箱(图2)内.模型箱为规则长方体,长6.7 m、宽1.7 m、高2 m.由于试验条件的限制,设计双线轨道结构、路基和地基模型缩尺比例为1/4.缩尺模型由钢轨、扣件系统、轨道结构(含轨道板、砂浆层、支承层)、路基(含基床表层、底层、路堤)和地基组成.
2.1.1钢轨和扣件系统
钢轨原型为我国60 kg·m-1标准钢轨,弹性模量为210 GPa,密度为7 800 kg·m-3,缩尺计算后采用5 kg·m-1轻型钢轨.对于WJ7-B型扣件系统规范规定弹性垫层静刚度为20~30 kN·mm-1,通过参考相关文献[13],并经评估后采用螺栓、相应钢轨扣板和橡胶垫板.

图2 加载系统和轨道-路基模型结构
2.1.2轨道结构
轨道结构主要由轨道板、砂浆层、支承层组成,原型轨道结构采用CRTS II型无砟轨道,长度、强度和配筋经缩尺计算后进行支模施工.首先开始上部轨道板的施工,在模板内先固定连接扣件的螺栓,安放编制好的铁丝网(图3),混凝土现浇之后对其进行养护.

图3 轨道板支模(平面)
同时对支承层进行施工,固定木质模板,安装吊环,混凝土现场浇筑养护;28 d后拆模,在支承层上浇筑约8 mm厚的砂浆,再吊装轨道板至砂浆层上,待8 h砂浆初凝后(图4),将轨道板落下,对轨道结构覆盖薄膜和土工布进行养护.
轨道结构养护完成后,进行钢轨和扣件的安装(图5),通过螺栓、扣板和垫板连接二者并最终固定于轨道板上预留的螺栓上.
2.1.3路基结构
路基结构包括基床表层、底层和路堤,缩尺后路基模型各层厚度分别为10、57.5和50 cm,模型坡度为1∶1.5.通过1.2节土样相同配比来配置各层填料,采用分层填筑振动夯实的方法,通过取样测量波速、密度等来保证填料质量.基床表层采用青石子掺5 %水泥(图6),分层填筑,每层虚铺厚度2 cm,夯土机夯实至1 cm,达设计各层标高后,对每层抽样检查,采用灌水法测密度,烘干法测填料含水量,采用试样现场测试的方式测试剪切波速;基床底层采用中砂、高岭土和水按质量比87∶13∶12.5混合(图7),属于B组填料,分层填筑,按压实度95%压实,每层虚铺厚度6 cm,夯实至5 cm;基床以下路堤采用中砂、高岭土和水按质量比100∶15∶12.5混合,属于B组填料,分层填筑,按压实度90%压实,每层虚铺厚度6 cm,夯实至5 cm,达设计各层标高后,对每层抽样检查,环刀法测试填料密度,烘干法测填料含水量.采集除表层外的各层样本进行GDS公司弯曲元试验测试波速.层与层之间需进行打毛,使得各层之间能够更好接触.

图4 轨道结构施工(侧面)

图5 钢轨、扣件安装
2.1.4地基
地基材料为1.2节经波速试样测试过的上海深层软土,缩尺后厚度为50 cm,每层虚铺厚度6 cm,夯实至5 cm,通过取样测量波速和密度来保证填料质量.达到设计各层标高后,对每层抽样检查,环刀法测试填料密度,烘干法测填料含水量,由GDS弯曲元试验测试波速.

图6 模型基床表层填料拌合

图7 夯土机夯实路基
2.2 试验加载方法及输入荷载
列车荷载模拟加载系统由1个作动器和相应的反力框架(图2)构成.作动器输出荷载范围为0~16 kN,作动器最高频率工作时内置活塞的行程为200 mm,最大激振频率33 Hz时的最大动荷载为10 kN.作动器通过安装于其下方的加载梁,将荷载传递至两侧的钢轨上面,从而实现列车轮轴荷载的模拟和力的传递.反力框架装配于模型箱的正上方,以模型箱两侧的刚性顶梁和立柱作为竖向支撑.
作动器输入荷载波形为正弦波,荷载函数如下:
F=1 933sin 2πft+2 707
(8)
式中:F为作动器输出荷载,N;f为频率,Hz,作动器加载频率从1 Hz依次加到30 Hz;t为时间,s.
2.3 传感器布置
针对路基结构的动力响应,为满足测试分析需要,在路基不同位置分别埋设了7个加速度传感器(图8).1、2、3、4、5依次为距路基表面1.175、0.925、0.675、0.375和0.1 m的位置,6为路基表面轨道结构附近靠近路基边缘位置,7为路基表面中心位置.
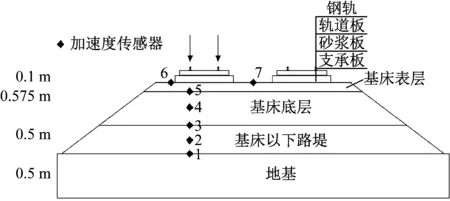
图8 传感器布置图
3 轨道-路基模型体系动力试验结果分析
3.1 路基各点加速度随时间的变化关系
路基加速度数据采用扬州晶明动态振动测试系统进行采集,每个通道采用独立24bits ADC(模数转换器),具有较高的信噪比,配接传递IEPE信号的加速度传感器,采样频率设为500 Hz.图9和10为25 Hz时钢轨下方路基中1~7位置处加速度的时程曲线.
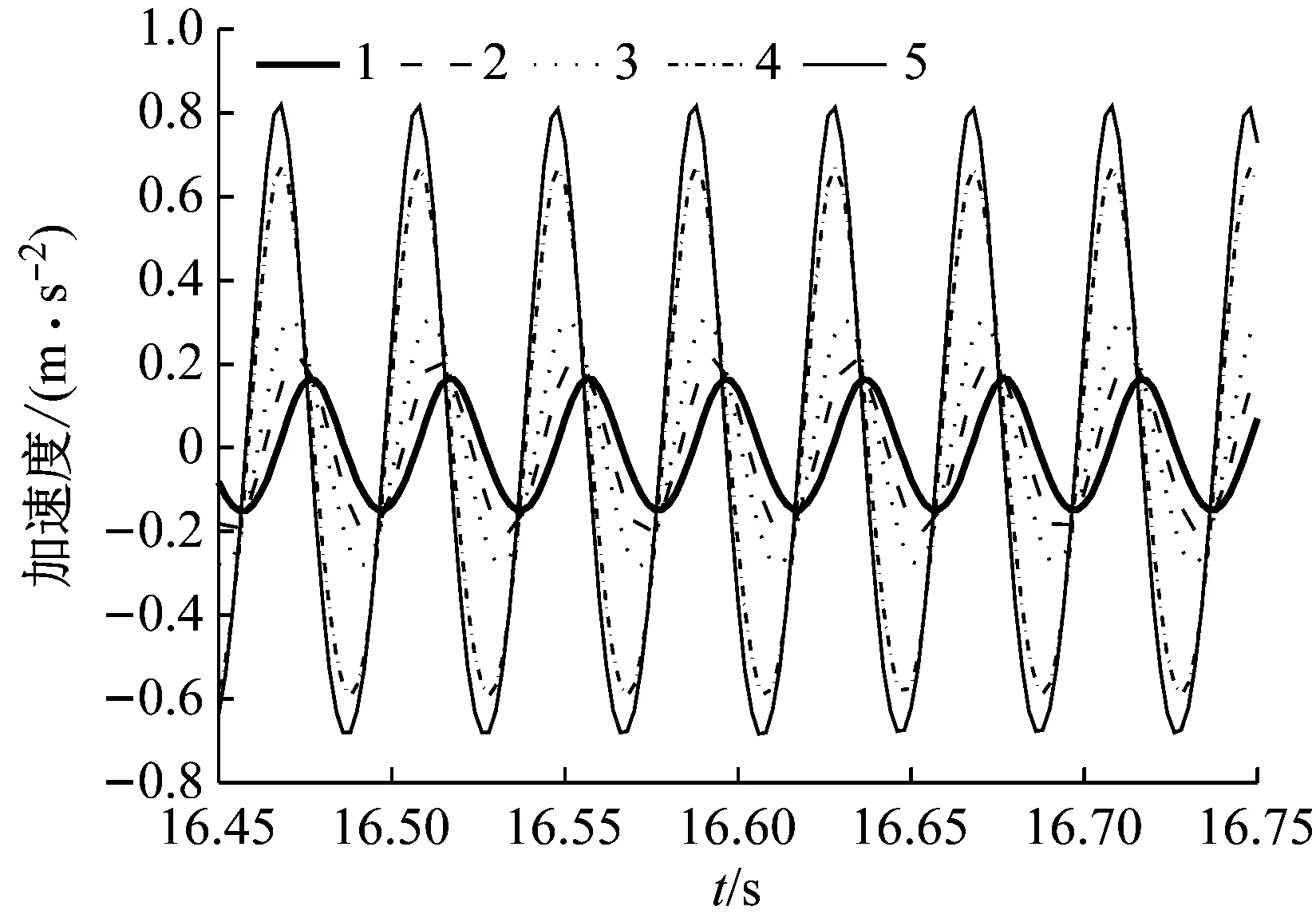
图9 25 Hz时钢轨下方路基1~5位置加速度时程曲线

图10 25 Hz时钢轨下方路基6~7位置加速度时程曲线
由图9可以看出,25 Hz时高频激振荷载下路基竖向加速度自上到下逐渐减少,最大峰峰值为1.502 m·s-2,位于基床表层底面(点5);传递至基床底层中部(点4)时,峰峰值下降到1.268 m·s-2;接着向下传递至路堤表面(点3)时,峰峰值下降到0.593 m·s-2;接着在路堤中传递和衰减,路堤中部(点2)的峰峰值为0.416 m·s-2;最后传递至路基最底部也就是地基表面处(点1),峰峰值降为0.314 m·s-2.,该值为最大加速度峰峰值的1/5,这说明能量主要在上部路基结构中衰减.
由图10可以看出,路基表面中心处的加速度峰峰值(点7)为0.906 m·s-2,约为路基表面边缘处(点6,0.494 m·s-2)值的1.83倍,说明路基表面中心振动更剧烈.但因路基表面边缘处(点6)更接近轨道结构,故点6要先于路基表面中心(点7)到达峰值位置.
图9和10可以看出,加速度由上至下在空间范围内的衰减效应和时间尺度上滞后(Time delay)效应非常明显.加速度时间尺度上滞后效应,表现在各个位置到达峰值点的时间差.从图中可以看出,钢轨投影下方,地基表面处(点1)、路堤中部(点2)、路堤表面(点3)和基床底层中部(点4)到达峰值点的时间分别比其上位置滞后0.004、0.002、0.002和0.001 s.其中点2与点1、点3等距,点4与点3、点5等距,但滞后时间却不一致,位置越靠上,到达峰值点相差的时间越短,说明能量在路基结构中传递过程中速度先快后慢,逐渐减小.
对激振频率为25 Hz时路基各点加速度时程曲线进行频谱分析,结果如图11、12所示.
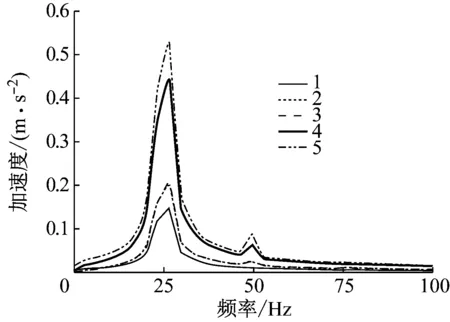
图11 路基1~5位置加速度频谱曲线
由图11、12可以看出,在同一激振频率下,不同位置处的加速度频谱分析的特征频率值相同,且与激振频率一致.
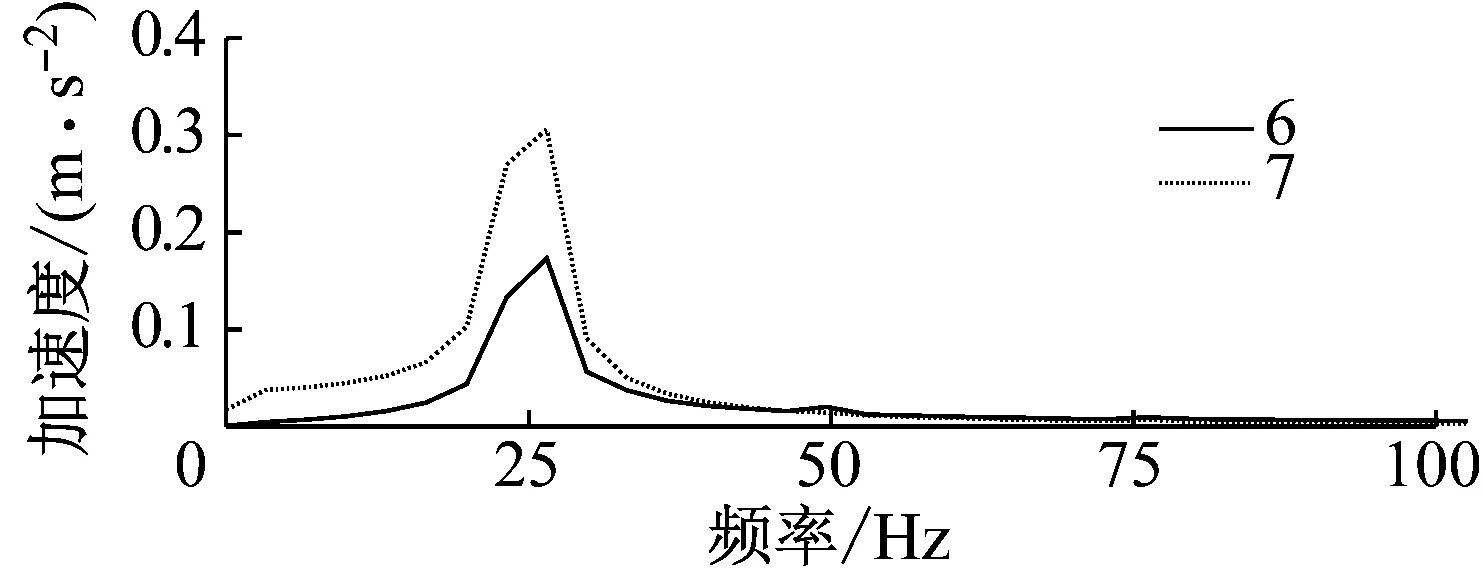
图12 路基6~7位置加速度频谱曲线
3.2 不同频率下路基的动力反应规律
为了研究试验模型体系的自振频率以及不同频率对轨道-路基模型结构的影响,对模型进行了从1 Hz到30 Hz的激振,得到了不同频率下路基内部各点的加速度振动峰峰值,如图13所示.
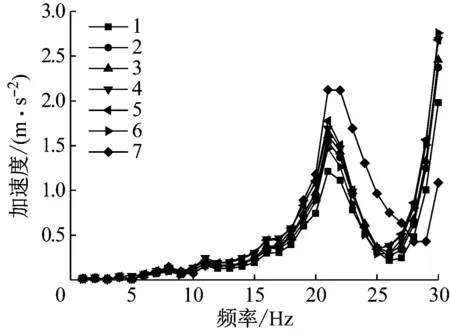
图13 路基内部各点加速度随频率变化关系
Fig.13 Relationship between accelerations and frequency at various points within the subgrade
由图13可以看出,路基结构中的表层、底层与路堤各层振动特征在激振频率1~10 Hz范围内类似,说明表层、底层与路堤各层振动一致,近于一个整体在振动.激振频率超过10 Hz后,路基的动力特征开始表现出来,各点的加速度峰峰值明显增大.当激振频率为21 Hz时,各点加速度到达峰值,超过该频率后,动态加速度值急剧减小.在频率超过25 Hz后,路基结构(除点7)的振动随着激振频率的增加又开始增长.路基结构内部振动加速度随激振频率的变化规律,可以用激振频率与体系多阶固有频率的关系来解释,因此从图中可以看出II型轨道-路基结构体系一阶固有频率为21 Hz,当激振频率越接近该固有频率时,体系内各点的加速度值突然很大,振动非常剧烈.21 Hz之后,相对于路基内部,路基表面中心动态竖向加速度与其他各点的表现有所不同,加速度的拐点出现在了29 Hz时,超过该频率,该位置的振动随着激振频率的增加才继续增长.
表4列出了不同激振频率下的加速度数据和放大数据.
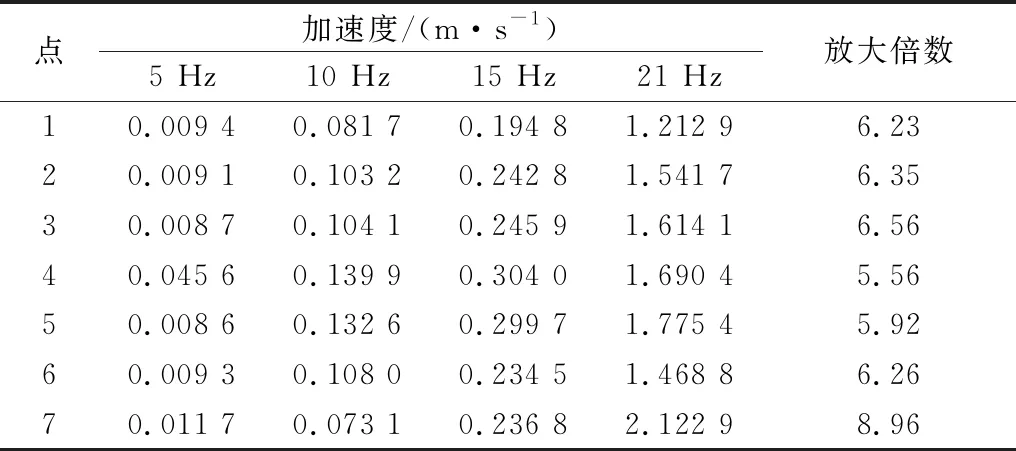
表4 II型轨道路基结构不同频率下的加速度数据
由表3可以看出,当激振频率低于15 Hz时,动态加速度随着激振频率的增加而缓慢增大.在频率5~10 Hz范围内,基床表面中心处的竖向加速度从0.011 7 m·s-2增长到0.073 1 m·s-2;基床表面支承层附近的竖向加速度从0.009 3 m·s-2增长到0.108 m·s-2;距离路基顶面0.1 m处的竖向加速度从0.008 6 m·s-2增长到0.132 6 m·s-2;距离路基顶面0.375 m处的竖向加速度从0.045 6 m·s-2增长到0.139 9 m·s-2;距离路基顶面0.675 m处的竖向加速度从0.008 7 m·s-2增长到0.104 1 m·s-2;距离路基顶面0.925 m处的竖向加速度从0.009 1 m·s-2增长到0.103 2 m·s-2;距离路基顶面1.175 m处的竖向加速度从0.009 4 m·s-2增长到0.081 7 m·s-2.
当激振频率提高到15 Hz时,各个位置处竖向加速度的增长速度都有显著提高,除去路基表面,在路基内部,大体表现为距离路基表面越远,竖向加速度越小.在频率为15~21 Hz范围内,竖向加速度随着激振频率增加而快速增长,并很快达到峰值.在距离路基表面0.1,0.375,0.675,0.925和1.175 m的5个深度处的竖向动态加速度分别较15 Hz时提高了5.92倍、5.56倍、6.56倍、6.35倍和6.23倍.路基表面支承层附近和路基表面中心的竖向动态加速度分别较15 Hz时提高了6.26倍和8.96倍.可以看出,处在自振频率工况下,路基表面中心处的加速度动力放大现象最为明显.当激振频率超过该一阶固有频率到25 Hz范围内,加速度值急剧减小.在此之后,基床表面中心处的加速度随着频率的增加仍会保持减小的趋势,直至29 Hz;而对于基床表面支承层附近点和距离路基表面0.1,0.375,0.675,0.925和1.175 m处的加速度随着激振频率的增加而展现出迅速增加的趋势,直至出现二阶固有频率.
3.3 不同频率下路基加速度的衰减规律
动力模型试验的竖向振动加速度峰峰值在不同频率下沿着路基竖向断面的分布特征如图14所示.
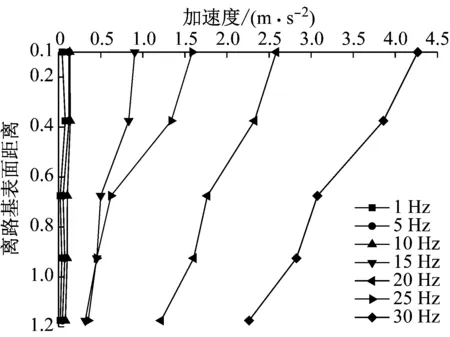
图14 各点加速度沿着路基横断面的分布特征
Fig.14 Distribution characteristics of accelerations along the cross section of roadbed at various points
由图14可以看出,基床底层以上的衰减速度远远高于路堤层.频率从1 Hz增大到20 Hz时,各点竖向加速度峰峰值也在逐渐增大,由3.2节研究可知,试验模型体系自振频率为21 Hz,在21~25 Hz频率范围是下降段,故25 Hz各点竖向加速度数值小于20 Hz情况,之后缓慢上升.在频率为25 Hz时,基床表层底部(路基表面下0.1 m)的竖向振动加速度峰峰值为1.588 1 m·s-2,迅速减小到基床底层底部(路基表面下0.675 m)处的0.621 9 m·s-2,随着离路基表面距离的增大,竖向振动加速度慢慢衰减至地基表面(路基表面下1.175 m)处的0.351 9 m·s-2s.
4 足尺数值模型路基加速度结果与模型试验结果对比
采用大型有限元软件ABAQUS建立了CRTS II型无砟轨道路基足尺有限元模型,其中基床表层弹性模量为800 MPa,地基弹性模量为40 MPa,激振荷载采用轴重为14 t激振频率为25 Hz的正弦荷载(其余参数见文献[32]).选取试验测试关键点(图8点1~6)作为对比对象,将试验所得路基加速度反推至原型(Sa=1),并与数值模型计算结果进行比较,见表5和图15.可以看出足尺数值模型中各点幅值和缩尺试验中各点结果对应较好,对比结果验证了所提试验设计方法的可靠性.

表5 路基加速度数值计算与试验数据
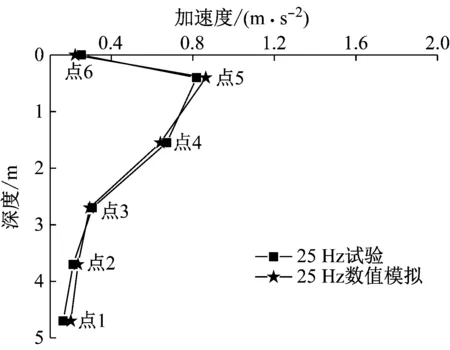
图15 路基加速度模拟结果与试验结果对比
Fig.15 Comparison of numerical simulation and experimental results of subgrade acceleration
5 结论
(1) 提出了轨道-路基体系一致动力相似设计方法,并进行了轨道-路基结构的相似设计、模型制作和动力试验,方法的可靠性得到了验证.
(2) 发现了加速度在向下传递过程中存在时间尺度上的滞后效应,越接近路基表面位置的加速度传感器,到达峰值点相差的时间越短,说明能量传递是一个先快后慢的过程.
(3) 同一激振频率下,路基不同结构层处加速度频谱分析的特征频率一致,说明虽然路基由散粒材料构成,但其仍是以共同工作的整体参与了动力传递和衰减.
(4) 确定了轨道-路基试验模型体系一阶固有频率值为21 Hz.
致谢:上海交大张璐璐教授等提供了地基和部分路基材料并参与了模型施工,在此特致以谢意.
