嫦娥三号激光三维成像系统全链路误差分析与仿真

栾奎峰， 童小华， 舒 嵘， 刘世杰， 徐卫明，谢 欢， 刘向锋,， 金雁敏， 陈 鹏， 王凤香

(1．同济大学 测绘与地理信息学院，上海 200092；2. 上海海洋大学 海洋科学学院，上海 201306；3. 中国科学院 上海技术物理研究所，上海 200083)

“嫦娥三号”探测器于2013年12月14日21时11分成功软着陆在月球表面，是我国首次地外天体软着陆任务, 也是在世界上首次成功实现了利用激光三维成像技术的地外天体软着陆自主避障[1-4].激光三维成像系统是探测器搭载的重要载荷，用于嫦娥三号探测器软着陆悬停避障段在极短成像时间内获取视场内着陆区精准三维高程数据，完成着陆器下降悬停段的精避障，保证着陆器高可靠、高安全的月表软着陆[3].

嫦娥三号的激光成像系统采用单脉冲激光发射、多元阵列探测器并行接收和双振镜快速扫描的新体制，能够在0.1 s内实现30°×30°着陆视场的快速扫描[5-6].由于硬件制造工艺、安装工艺和实际使用环境等影响，激光成像系统原始观测数据中都存在系统性和偶然性的误差，导致着陆区障碍探测结果的不确定性.目前，提高激光三维成像的精度和可信度的方法主要是对误差进行检校，常用的是通过基于面特征的检校和基于点特征的检校两种[7-14].在成像全链路中，各单元共同协作，完成激光测距系统的多通道测距和扫描系统中水平角竖直角的观测与记录，获取激光成像系统的原始观测数据，并反演三维点云.激光三维成像测距链路和二维振镜扫描测角链路等每个环节的误差因素均会对激光点云反演的精度和三维成像的质量产生影响.目前对多波束阵列探测和二维振镜扫描成像新机制的激光成像系统全链路误差的研究较少，需要对激光三维成像系统的成像全链路中影响成像质量的因素进行分析，确定影响成像质量的主要误差因素，并研究误差控制和提高成像精度的方法.

针对嫦娥三号激光三维成像系统探测精度的工程需求，本文提出了一种多波束激光成像系统的全链路误差分析与仿真方法，分析多波束阵列探测、二维振镜扫描的成像链路和误差因素，仿真分析各因素对成像精度的影响规律和最大可能的误差，并提出各误差因素的控制方法.该方法已实际用于嫦娥三号激光三维成像系统，为该系统首次成功用于地外天体软着陆悬停避障提供了技术支撑.

1 嫦娥三号激光三维成像系统的成像全链路解析

嫦娥三号激光三维成像系统从成像的结构上，可分为激光发射、激光偏转、激光接收、温度控制和激光行走时间测量等单元，基本原理如图1所示.

图1 多波束激光三维成像系统的成像全链路解析

激光驱动器驱动半导体激光器(Laser Diode，LD)发射出一个短脉冲，并且将脉冲分成两部分，一部分作为主脉冲发射，由主波探测器接收，经过整形电路硬件后，将数字信号转换成模拟信号，启动时间测量单元，记录本次激光脉冲的开始时间；另一部分脉冲经过激光整形器和分栅器后，通过由水平振镜和竖直振镜组成的双振镜扫描系统，将发射激光光束反射到目标表面的不同位置，经过目标后向散射后的回波信号，经同光轴设计的系统光线传输，由高灵敏度的线阵雪崩光电二极管 (avalanche photo diode，APD)探测器对多个激光通道的回波信号进行接收，经过整形电路装置的数模转换，记录本次脉冲的结束时间.由此进行时间间隔测量，得到本次激光脉冲的时间间隔，即可计算出本次脉冲激光对应的多个激光通道的测距值；使用单次测量的多个通道距离测量值和水平振镜、竖直振镜的角度测量值，应用多元激光器虚拟焦点成像模型，最终实现多波束激光三维成像系统的快速高精度点云反演与成像.

2 激光三维成像系统全链路误差模型

激光三维成像系统的成像链路误差，按照其观测的要素信息，总体上分成测距链路和测角链路两种主要因素.

2.1 测距链路误差

多波束激光测距采用的是单激光脉冲式测距，其测距链路中的误差主要为固定延迟误差、时钟频率漂移误差、时间间隔测量误差、数字上升沿抖动误差和时刻鉴别误差.按误差因素对激光测距影响的性质，可将测距的固定延迟误差和时钟频率漂移误差分为系统性误差，时间间隔测量误差、数字电路上升沿抖动误差和前沿鉴别误差分为偶然性误差.本文对这两类误差进行分析.

2.1.1测距链路系统性误差

系统误差主要是测距链路中对时间测量的精度产生影响、具有一定规律性的误差因素.测距链路的固定延迟误差存在于激光测距链路中的时间间隔测量、主波探测器、多回波探测器响应时间测量等不同环节,根据脉冲激光的测距方程，可以换算为距离固定延时误差值εd为

(1)

式中：ΔTd为测时系统产生的误差，c为真空中的光速.对于多波束类型的激光成像系统不同通道的误差不相同.

时钟频率漂移误差εdf是同步时钟信号的频率发生漂移产生距离测量误差，可表示为

εdf=R·edf

(2)

式中，R为距离测量值，edf为时钟稳定度.时钟频率的漂移和环境温度、供电电压有关，是一个缓慢变化的过程.

2.1.2测距链路偶然性误差

测距链路的随机误差因素主要包括时间间隔测量误差、数字电路上升沿抖动误差和前沿鉴别误差等.

脉冲式多波束激光的时间间隔测量电路采用同步计数器来实现，其振荡频率决定了一个有限的时间分辨率，时间间隔测量误差σn的表达式为[15]：

(3)

其中：f为计数器频率.

数字电路上升沿抖动误差是由于脉冲激光信号经过放大后，需要由阈值鉴别芯片转化为数字电平，以触发时间间隔测量而引发的误差，测距中误差σj：

(4)

式中：σjm为激光测距主通道回波上的中误差.

前沿鉴别误差是由于测距系统在前沿鉴别法的鉴别电路中因信号上升沿比较宽并且叠加了噪声，使模拟信号的上升沿穿越比较阈值的时间发生了变化.采用恒比定时电路后的鉴别误差σie为

(5)

其中：fn(t)为比较器处的噪声电压；fc(t)为比较器输入端的电压差，tr为上升沿时间；SNR为信噪比(SNR)；k为衰减器的衰减系数，k越小，则恒比定时鉴别法的标准偏差越小.但过小的衰减系数将使经过衰减器的信号的信噪比减小，反而增大标准差，所以k的大小一般通过实验最终确定.

2.2 测角链路误差分析

光束偏转单元的误差会对扫描角产生一定的影响，包括对水平扫描角度和垂直扫描角度的影响.二维振镜测角链路的系统性误差包括编码器误差、旋转轴轴系误差和振镜的电机转动引起的微小振动等误差，偶然性误差包括入瞳漂移、随机噪声干扰和环境温度等因素.

2.2.1编码器误差

振镜的编码器误差在水平振镜和竖直振镜两个方向均存在.由于水平振镜不同扫描带振镜摆动方向相反，水平角度编码器零点误差(B1)对水平角的影响Δθx可以表示为：

Δθx=±B1

(6)

水平振镜对激光三维成像的影响在相邻扫描带之间是正好相反的.

竖直振镜的摆动方向为一个方向,其编码器误差C1对竖直角观测值Δθy的影响可以表示为

Δθy=C1

(7)

2.2.2轴系结构误差

二维振镜偏转单元的扫描系统中，视准轴误差(B2)是视准轴与水平轴的法线之间的夹角，对水平角测量带来的影响Δθx可以表示为

(8)

水平轴(横轴)误差是水平轴与垂直轴的法线的夹角(B3)，对水平角测量的影响可以表示为

Δθx=B3·tanθy

(9)

除此之外，还有一些如入瞳漂移、随机噪声干扰和环境温度引起的振镜镜面变形等误差因素，这些因素也会影响测角和测距的精度，可按照偶然性误差的性质，对其精度进行评定.

2.3 激光三维成像系统全链路误差控制

根据嫦娥工程避障探测精度需求，激光三维成像系统需要将测距精度控制指标分解到其成像链路的各个环节.其中，测距链路的误差直接影响激光三维成像系统的测距精度，而测角链路误差主要影响激光光束的指向，且间接地影响激光三维成像系统的测距精度，主要是Z方向的影响.根据前期建立的激光三维成像系统的严密成像方程[6]，Z坐标可表示为

(10)

其中，i为激光探测通道编号，ri为第i个激光探测通道的距离观测值，θx为水平角观测值，θy为竖直角观测值；θi为激光器第i个探测单元和脉冲时激光中心的竖直夹角，因嫦娥三号激光三维成像系统为16波束，则有θi=17-2i；b和e是已知的仪器设计参数，分别为激光光源与水平振镜中心距离以及竖直振镜和水平振镜中心之间距离，通常为已知量；ni为第i个激光通道的向量.

由此，上述Z方向坐标分量关于水平角、竖直角和测距观测量的函数可以表示为

z=f(ri,θx,θy)

(11)

对公式(11)进行全微分，则有：

(12)

其中，

(13)

(14)

(15)

根据误差传播律，Z坐标分量的方差为

(16)

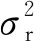
(17)

(18)

将式(16)代入式(18)，则可建立公式(19)如下：

(19)

由于二维振镜的加工工艺基本一致，可认为两个角度中误差相等，即σθx=σθy，则式(19)可以变化为

(20)

对激光三维成像系统的数据中每个点云计算其角度中误差σθi，选择出现的最大角度中误差为允许误差.而水平角的观测值系统误差可以表示为

σθx=σB1+σB2·secθy+σB3·tanθy

(21)

σB1,σB2,σB3是水平振镜硬件的测角系统性误差项的中误差，为同等精度观测，则可假设三者相等，用符号σB表示.式(21)可表示为

σθx=σB·(1+secθy+tanθy)

(22)

式(22)为关于竖直角观测值的函数，将原始数据的竖直角观测值代入式(22)中，可计算出多个σB值，并选取最大值为最大允许误差，则可计算出σθx和σθy的最大允许中误差.

3 嫦娥三号激光三维成像系统全链路误差仿真与分析

为了分析各链路误差对该激光成像系统的影响规律，并确定误差的控制方法，本文以嫦娥三号激光三维成像系统为例，仿真对沿主光轴方向距仪器100 m处平面的成像，分析各链路误差对成像的影响规律，保证系统的设计满足嫦娥工程所要求的精度(100 m成像距离时测距精度优于20 cm).

3.1 测距链路误差仿真与分析

3.1.1测距链路系统性误差

嫦娥三号激光三维成像系统的测距通道数量为16，根据实验室测试数据，各通道的固定延时误差在±0.80 m之内，用随机函数的方法生成各通道的固定延时误差，并作为各通道的虚拟固定延时测距误差的模拟值，模拟结果如图2所示.

从图2结果看，X、Y方向的影响规律是成像视场中心位置影响最小，越靠近四周，误差影响越大.同一通道Z值的偏离量，成像中心(X=0、Y=0)处的误差影响最大，等于模拟的测距固定误差，越靠近四周时，Z值的影响减小，从点云图表现为靠近中心偏离值大、靠近两端向Z方向靠近的弧线.

在多元激光成像链路的温度控制和补偿结构中，嫦娥三号激光器的有偿晶体振荡器的稳定度edf能够达2×10-6[16]，根据公式(2)，时钟频率漂移误差的仿真结果如图3所示.

图2 多通道固定延时误差仿真结果

图3 时钟频率漂移误差仿真结果

从图中可以发现，单个扫描带中不同探测单元出现了明显的条带性差异，主要原因是不同探测单元的测距值不同，而时钟频率漂移误差为乘常数，则会对不同探测单元产生不同的影响所致，在X和Y方向的影响是成像视场中间部分较小，以同心圆形式，向成像视场外围靠近时，测距误差影响增大；Z方向的影响是视场中心区域最大，向视场四周扩散时，Z方向影响减小.但影响是在10-7m数量级，远小于一般障碍探测精度，在对障碍探测应用的激光三维成像系统的系统误差检校中可不考虑本误差项.

3.1.2测距链路偶然性误差

嫦娥三号激光器的单个测距链路的通道时间分辨率可以做到1.25×10-10s的时间测量精度，则计算的时间间隔测量中误差σn≈0.77 cm；数字电路上升沿抖动对时间测量的影响约为20 ps，由此产生的中误差σj为0.4 cm；当激光器的衰减系数取值为k=0.3，回波上升沿tr=7 ns，设计的信噪比SNR>31时，前沿鉴别中误差σie=3.3 cm，则激光测距链路总的测距随机误差为

(23)

对所有的探测单元测距值增加相同的随机误差，其仿真结果如图4所示.

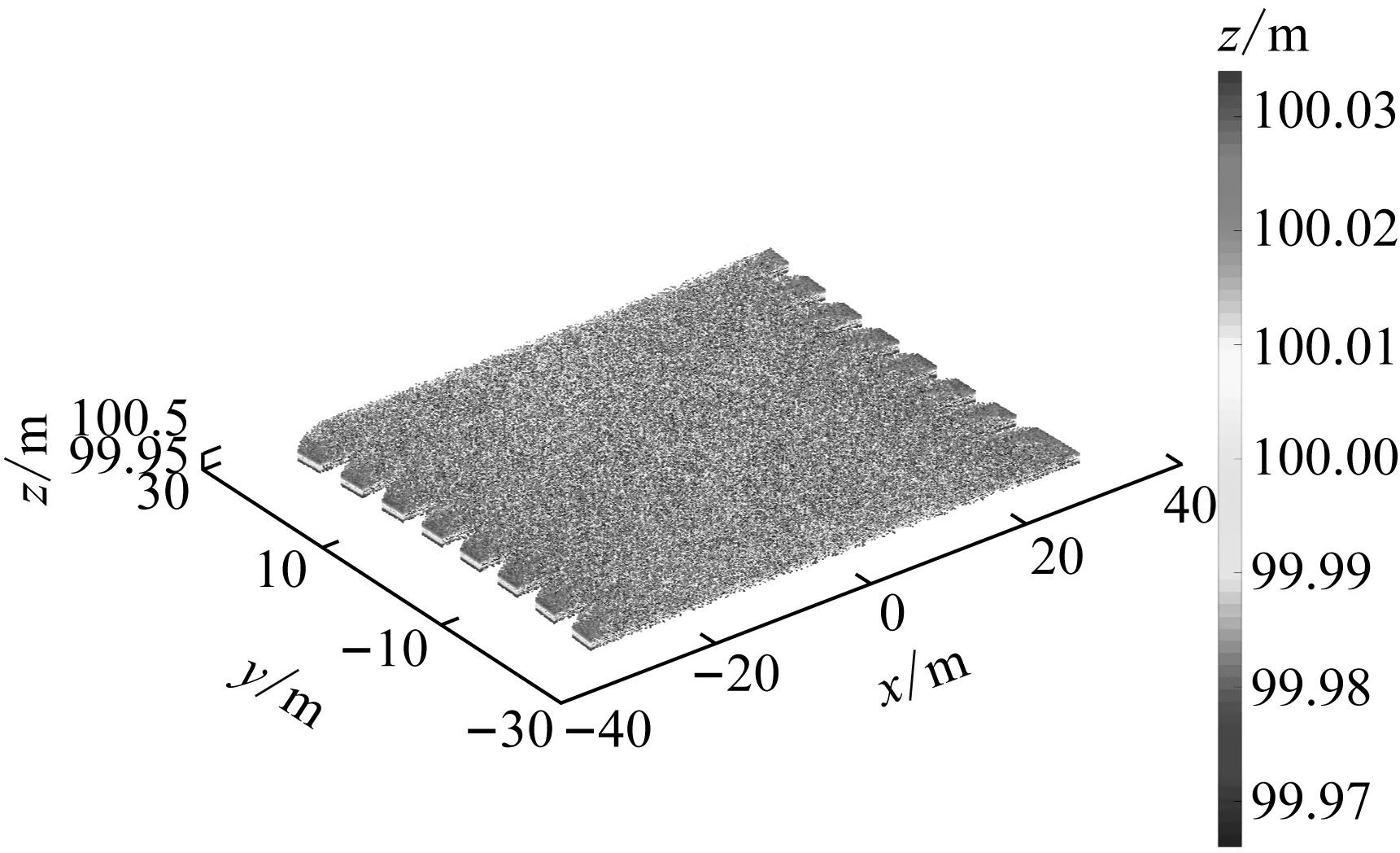
图4 测距链路随机误差仿真结果

其随机误差主要对Z方向有影响，并且全视场范围内的影响大小基本一致，而对X、Y方向基本没有影响；对Z方向的影响为(3.4～-3.3 cm)，与设定的随机误差区间(±3.4 cm)基本一致.

假设固定延时误差可以采用合理的控制方法将误差控制在5 cm之内，时钟频率漂移误差可忽略不计，根据公式(17)可计算出激光测距链路所产生的最大中误差σr≈6.04 cm.

3.2 测角链路误差仿真与分析

将测距链路最大允许误差σr代入公式(19)，可计算出最大的σB=42.9″.竖直角观测值系统误差项只包含竖直振镜编码器误差项，即σθy=σC1=94.5″.其中，σθy为竖直角观测值θy的中误差，σC1为竖直振镜编码器的中误差.

本文将各误差因素的1倍中误差为误差量，数值仿真分析各误差项对激光三维成像质量的影响规律和控制方法.图5～图8分别为水平振镜编码器误差、视准轴误差、水平轴误差和竖直度盘指标差对点云反演的影响仿真结果.

图5 水平振镜编码器误差仿真结果

从图5可以看出，水平振镜编码器误差对点云在X方向的影响较大，奇数扫描带沿X正方向出现向上斜坡，偶数扫描带沿X反方向出现向上斜坡，中间点云部位影响最小，图像上出现单数扫描带双数扫描带在扫描带水平中心位置的交叉.相比于X方向，Y方向和Z方向的影响很小.

图6 视准轴误差仿真结果

从图6中可以看出，视准轴误差影响的点云数据出现沿X方向的斜坡，X负值方向的点云Z值偏小，正值方向的Z值相对较大，靠近零点位置对Z值基本没有影响；点云X方向边界会向左侧整体偏移.

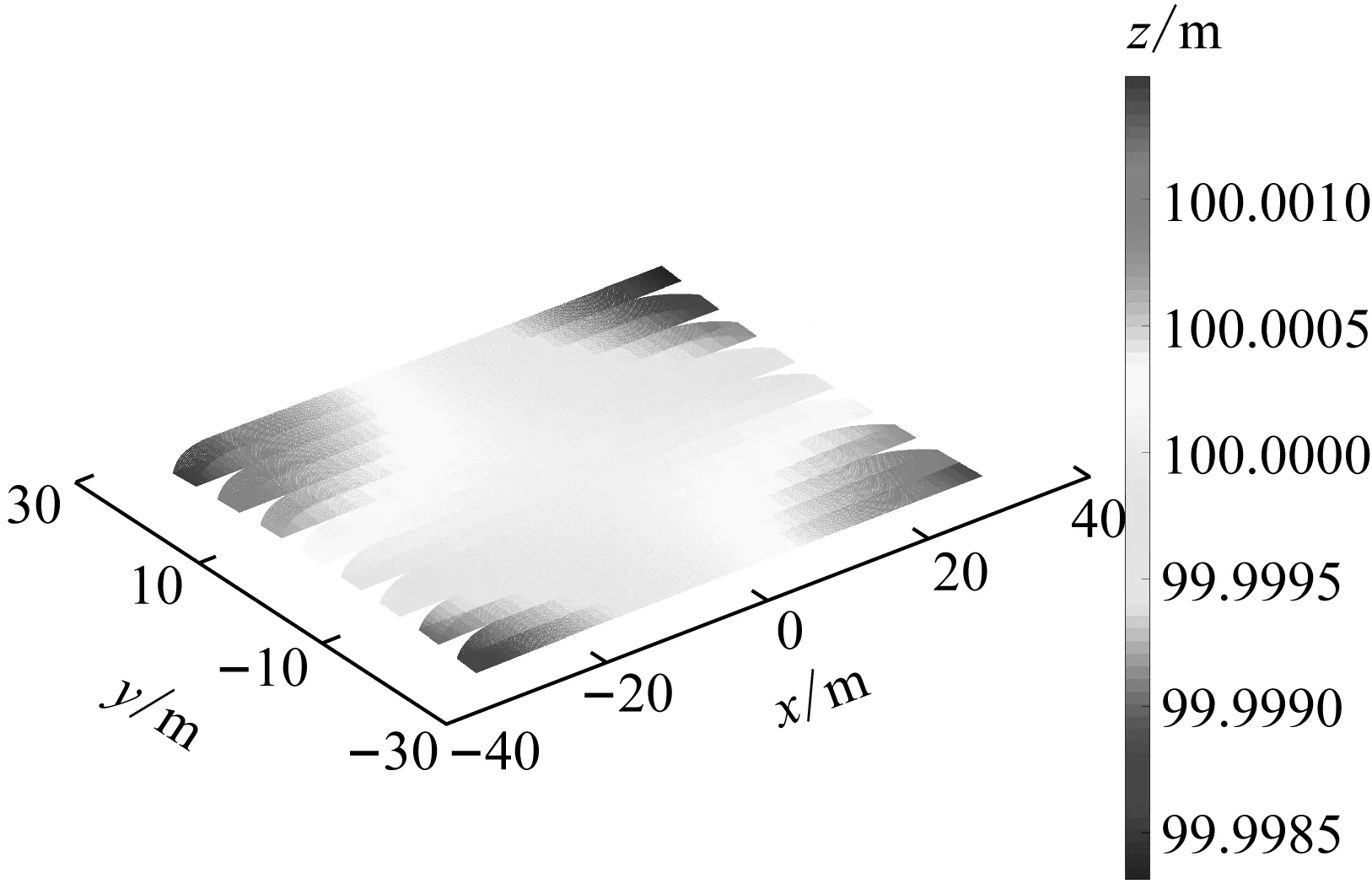
图7 水平轴误差仿真结果

从图7中可以看出，水平轴系统误差影响的三维点云数据在4个角的位置出现明显的差异性，左上角和右下角反演的点云Z值明显大于理论值，左下角和右上角的Z值小于理论值，这种现象在4个脚点位置最为明显，越靠近成像中心，这种现象呈现减弱趋势，在中心区域基本无变化.

从图8的仿真结果可以看出，竖直振镜的编码器误差会使点云沿Y轴出现上半部分Z值偏大、下半部分Z值偏小、中间无影响的斜坡，各探测单元的影响规律一致.各测角链路对点云反演的影响情况如表1所示.

从表1的数据中可以发现，同等误差量的条件下，水平振镜编码器误差对点云反演结果影响较大，Y方向的最大偏差绝对值达到9.17 cm，但对X方向没有影响；水平轴误差对点云反演的结果影响相对较小，最大偏差值出现在X方向，绝对值为0.57 cm.

图8 竖直度盘指标差仿真结果

误差项影响方向最大偏差绝对值/cm最小偏差绝度值/cmB1B2B3C1X00Y9.179.17Z2.610X4.344.17Y0.340Z1.280X0.570Y0040Z0.170X00Y9.179.17Z2.610

3.3 成像全链路误差因素综合仿真分析与控制方法

测距链路和测角链路的误差影响规律性不同，其最终均影响测距值的反演结果.综合3.1～3.2节关于测距误差参数模型、水平角参数模型和竖直角参数模型，建立了其综合误差影响的模拟，其仿真结果如图9所示.

从仿真结果可以看出，由于各测距通道延时误差的独立性，导致大部分点云偏离理论真值位置，而不同通道点云呈现系统性的密集分布现象，并且对测距精度的影响最大.同时，视场内的点云也出现明显的扫描带错位，使得X方向和Y方向出现斜坡现象，这与3.2节测角链路误差分析结果是一致的.

以嫦娥三号激光三维成像系统的精度控制为例，对成像链路中各误差对成像的影响规律进行分析，并且给出了各环节允许的最大误差以及误差的控制方法.

图9 成像全链路误差因素综合仿真结果

从表2中可以看出，影响激光三维成像系统成像质量和测距精度的因素很多，从误差源性质分类，主要为系统误差和随机误差.随机误差大部分和激光成像的硬件设计工艺相关，其误差控制可通过对硬件加工工艺环节和电路设计环节解决.而测距固定延时误差、编码器误差、轴系误差等系统误差对测距精度影响较大，并且受成像全链路误差影响的叠合效应，视场内局部范围的测距误差具有明显差异性，需要对其建立大视场范围的系统误差检校模型，开展大量的地面检校和验证实验，以修正系统误差参数，该部分研究另文介绍.

表2 成像全链路误差因素及控制方法

4 结论

为了精确控制嫦娥三号激光三维成像系统的测距精度和成像质量，本文提出了其全链路误差分析与仿真方法，实现了激光三维成像系统成像过程中影响其质量和精度的误差因素的全链路分析，并对测距链路系统性误差因素、测距链路偶然性误差因素、振镜测角链路和全链路因素等进行了建模，实现了成像链路中系统误差参数项和随机误差参数项对成像质量影响的仿真与误差控制.并由此确定了测距固定延时误差、振镜编码器误差、视准轴误差和水平轴误差等因素需要建立有效的地面检校和控制方法，以修正系统误差参数的方法提高成像精度.本文建立的激光三维成像全链路误差分析与仿真方法已实际用于嫦娥三号激光三维成像系统，为该系统首次成功用于地外天体软着陆悬停避障提供了技术支撑.同时，本文方法对多元探测新体制激光成像系统的误差分析与控制理论具有一定的指导和参考借鉴作用.