基于蒙特卡罗模拟的概率求解问题研究

袁佳婧

摘 要：蒙特卡羅模拟是通过计算机模拟实际发生的事情。通过蒙特卡罗模拟能计算出相应事件发生的概率，模拟与计算过程有效、可行、易理解。其基本思想是，将各种随机事件的概率特征与模拟联系起来，用试验的方法确定事件的相应概率与数学期望。应用蒙特卡罗模拟方法解决了实际概率问题，为解决用传统方法不能解决的问题，提供了有意义的参考。主要介绍蒙特卡罗方法及基本原理，并通过实例说明蒙特卡罗方法在数学建模中的应用。

关键词：蒙特卡罗模拟;随机试验;正态分布;数学建模

中图分类号：TB 文献标识码：Adoi：10.19311/j.cnki.1672-3198.2019.11.106

1 蒙特卡罗方法与基本原理

蒙特卡罗方法又称为计算机模拟方法，它是以概率统计理论为基础的一种方法。该方法与一般数值计算方法有本质区别，蒙特卡罗模拟采用的是频率近似概率的数学思想，来解决物理、数学、生产管理或工程技术等方面的问题。蒙特卡罗方法的起源，最早可以追溯到18世纪下半叶时，由Buffon提出的用试验的方法求值，即：蒲丰投针问题。蒲丰投针问题的解决方法就是蒙特卡罗模拟的典型运用。当时的投针试验是利用人工进行实际操作，然后统计试验结果，最后得出结论。但是人工进行大量实际的随机试验，一方面成本较高;另一方面统计结果的准确率较低，因此只能称Buffon试验只能称为近代统计模拟的雏形。随着现今计算机技术的高速发展，蒙特卡罗模拟实验已不再需要人工实际操作，通过计算机随机模拟更加方便快捷，所得的估计值也更精确。

蒙特卡罗模拟方法求解概率问题的基本思想是：当所求问题的解是某个随机变量的数学期望或者某个事件的概率，或者是与数学期望、概率有关的量时，通过试验的方法模拟事件的发生，求出该事件发生的频率，计算所求参数的统计特征，最后给出近似值作为问题的解。

2 实际问题

校车在每个工作日，都会在A校区与B校区之间摆渡。李华家住B校区附近。校车从A校区到B校区的运行时间服从均值为30分钟，标准差为2分钟的正态随机分布。校车大约中午13：00从A校区出发，李华大约13：30步行到达B校区，校车从A校区出发的时刻及概率如表1所示。

3 问题分析

记T1为校车从A校区出发的时刻，T2为校车从A校区到B校区运行的时间，T3为李华到达B校区的时刻。T1、T2、T3均是随机变量，且T2～N（30，22），T1、T3的分布律如表所示：其中记中午13时为时刻t=0。

通过分析可知，此人能及时赶上校车的充分必要条件是：T1+T2>T3。由此得到，此人赶上校车的概率是P{T1+T2>T3}。

4 建立模型

利用蒙特卡罗方法随机模拟校车出发时刻，校车车运行时间，李华到达B校区的时刻。然后判断多次试验中满足上述充要条件的试验有多少次。若在n次试验中，有k次成功，则用频率k/n作为李华能赶上校车的概率。当n很大时，频率值与概率值近似相等。

设r1，r2 是（0，1）区间上均匀分布的随机数。则T1，T3的分布律的模拟公式为：

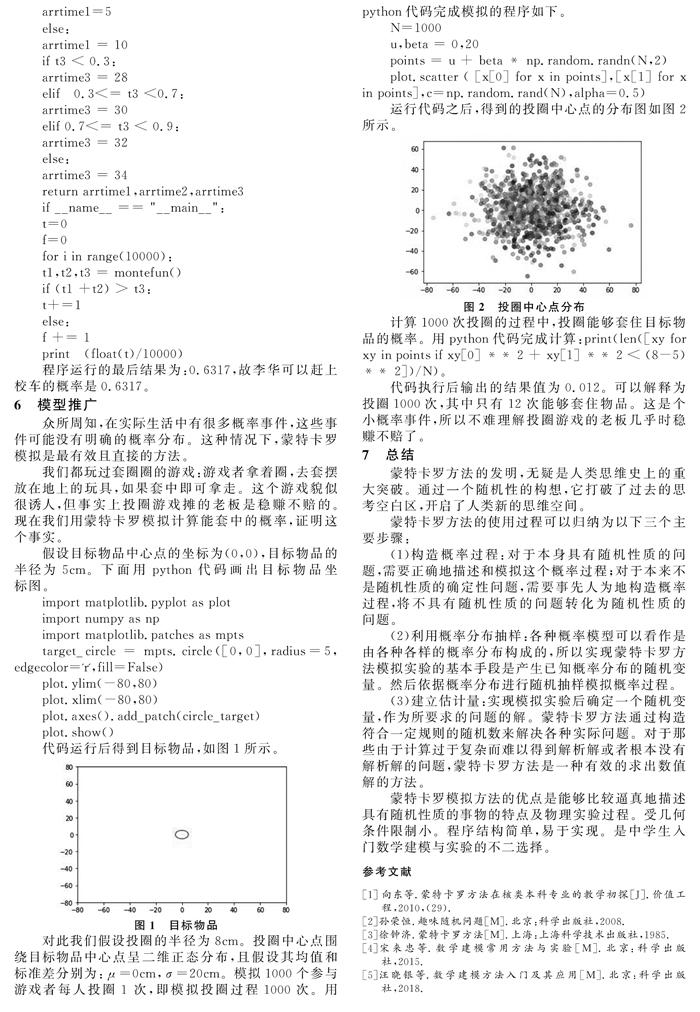
t1=0，0

令 t2 是服从正态分布N（30，22） 的随机数，则将t2 看成火车运行时间T2的观察值。

在每次试验中，产生两个U（0，1） 的随机数r1，r2，来构造 t1，t3。产生一个N（30，22） 的随机数r3，来构造 t2。当 t1+t2>t3，认为试验成功（能够赶上校车）。若在n次试验中，有k次成功，则用频率k/n 作为此人赶上火车的概率。当n很大时，频率值与概率值近似相等。

5 模型求解

下面是利用python语言进行蒙特卡罗模拟的程序。其中montefun（）是自定义的蒙特卡罗模拟函数。

import numpy as np

def montefun（）：

t1 = np.random.rand（）

t2 = np.random.normal（30，2）

t3 = np.random.rand（）

arrtime1=0

arrtime2=t2

arrtime3=0

if t1<0.7：

arrtime1=0

elif 0.7<=t1<0.9：

arrtime1=5

else：

arrtime1 = 10

if t3 < 0.3：

arrtime3 = 28

elif 0.3<= t3 <0.7：

arrtime3 = 30

elif 0.7<= t3 < 0.9：

arrtime3 = 32

else：

arrtime3 = 34

return arrtime1，arrtime2，arrtime3

if __name__ == "__main__"：

t=0

f=0

for i in range（10000）：

t1，t2，t3 = montefun（）

if （t1 +t2） > t3：

t+=1

else：

f += 1

print （float（t）/10000）

程序运行的最后结果为：0.6317，故李华可以赶上校车的概率是0.6317。

6 模型推廣

众所周知，在实际生活中有很多概率事件，这些事件可能没有明确的概率分布。这种情况下，蒙特卡罗模拟是最有效且直接的方法。

我们都玩过套圈圈的游戏：游戏者拿着圈，去套摆放在地上的玩具，如果套中即可拿走。这个游戏貌似很诱人，但事实上投圈游戏摊的老板是稳赚不赔的。现在我们用蒙特卡罗模拟计算能套中的概率，证明这个事实。

假设目标物品中心点的坐标为（0，0），目标物品的半径为5cm。下面用python代码画出目标物品坐标图。

import matplotlib.pyplot as plot

import numpy as np

import matplotlib.patches as mpts

target_circle = mpts.circle（[0，0]，radius=5，edgecolor='r'，fill=False）

plot.ylim（-80，80）

plot.xlim（-80，80）

plot.axes（）.add_patch（circle_target）

plot.show（）

代码运行后得到目标物品，如图1所示。

对此我们假设投圈的半径为8cm。投圈中心点围绕目标物品中心点呈二维正态分布，且假设其均值和标准差分别为：μ=0cm，σ=20cm。模拟1000个参与游戏者每人投圈1 次，即模拟投圈过程1000次。用python代码完成模拟的程序如下。

N=1000

u，beta = 0，20

points = u + beta * np.random.randn（N，2）

plot.scatter （ [x[0] for x in points]，[x[1] for x in points]，c=np.random.rand（N），alpha=0.5）

运行代码之后，得到的投圈中心点的分布图如图2所示。

计算1000次投圈的过程中，投圈能够套住目标物品的概率。用python代码完成计算：print（len（[xy for xy in points if xy[0] ** 2 + xy[1] ** 2 < （8-5） ** 2]）/N）。

代码执行后输出的结果值为0.012。可以解释为投圈1000次，其中只有12次能够套住物品。这是个小概率事件，所以不难理解投圈游戏的老板几乎时稳赚不赔了。

7 总结

蒙特卡罗方法的发明，无疑是人类思维史上的重大突破。通过一个随机性的构想，它打破了过去的思考空白区，开启了人类新的思维空间。

蒙特卡罗方法的使用过程可以归纳为以下三个主要步骤：

（1）构造概率过程：对于本身具有随机性质的问题，需要正确地描述和模拟这个概率过程;对于本来不是随机性质的确定性问题，需要事先人为地构造概率过程，将不具有随机性质的问题转化为随机性质的问题。

（2）利用概率分布抽样：各种概率模型可以看作是由各种各样的概率分布构成的，所以实现蒙特卡罗方法模拟实验的基本手段是产生已知概率分布的随机变量。然后依据概率分布进行随机抽样模拟概率过程。

（3）建立估计量：实现模拟实验后确定一个随机变量，作为所要求的问题的解。蒙特卡罗方法通过构造符合一定规则的随机数来解决各种实际问题。对于那些由于计算过于复杂而难以得到解析解或者根本没有解析解的问题，蒙特卡罗方法是一种有效的求出数值解的方法。

蒙特卡罗模拟方法的优点是能够比较逼真地描述具有随机性质的事物的特点及物理实验过程。受几何条件限制小。程序结构简单，易于实现。是中学生入门数学建模与实验的不二选择。

参考文献

[1]向东等.蒙特卡罗方法在核类本科专业的教学初探[J].价值工程，2010，（29）.

[2]孙荣恒.趣味随机问题[M].北京：科学出版社，2008.

[3]徐钟济.蒙特卡罗方法[M].上海：上海科学技术出版社，1985.

[4]宋来忠等.数学建模常用方法与实验[M].北京：科学出版社，2015.

[5]汪晓银等.数学建模方法入门及其应用[M].北京：科学出版社，2018.