大气污染物SO2空间相关性的空间集聚分析

刘梅 张冬有

摘要：以东北三省2017年的大气污染物SO2为研究对象，通过全局指标（全局Moran指数、Geary系数）、区域型指标（Morans I、局部Gearys C、局部Getiss G）等，对SO2的空间聚集情况进行分析计算，比较两种指标的探测结果。结果表明，在全局型空间自相关的分析中，Moran指数、Gearys C两个指标均表明东北三省SO2存在显著的空间自相关性;Moran散点图、LISA集聚图、局部G系數集聚图等均揭示了东北地区36个地级市SO2的局部空间相关性，即低值集聚区（冷点）主要集中在研究区东部，（热点）高值集聚区集中在研究区的西南部;通过对两种指数的分析可发现，在研究区的西南部，营口、大连、铁岭3个地区在Moran指数中为低-高集聚区，黑河为不相关地区，但在局部G系数中，营口、大连、铁岭为热点（高-高集聚），黑河为冷点（低-低集聚区），结合实际情况，对分析SO2空间相关性来说，Moran指数相对G系数的分析结果更优。

关键词：空间统计;空间自相关;全局指标;区域指标;GIS;SO2

中图分类号：X511         文献标识码：A

文章编号：0439-8114（2019）08-0056-04

DOI：10.14088/j.cnki.issn0439-8114.2019.08.012           开放科学（资源服务）标识码（OSID）：

Abstract： Taking the atmospheric pollutant SO2 of the three northeastern provinces in 2017 as the research object， through global indicators （global Moran index， Geary coefficient）， and regional indicators（MoranI， local Gearys C， local Getiss G）， the spatial aggregation of SO2 was analyzed and calculated. The detection results of the two indexes were compared. The results showed that in the analysis of spatial autocorrelation， the Moran index and Gearys C index both indicated that there was significant spatial autocorrelation in SO2 in the three northeastern provinces; Moran scatter plot， LISA agglomeration map， and local G cluster agglomeration etc. all revealed the local spatial correlation of SO2 in prefecture-level cities in 36 prefecture-level cities in northeast China， That is， the low-value clusters （cold point） are mainly concentrated in the eastern part of the research area， and the high-value clusters （hot point） are concentrated in the southwest part of the research area; Through the analysis of the two indices， it could be found that in the southwestern part of the research area， Yingkou， Dalian and Tieling are low-high agglomeration areas in the Moran index， and Heihe is an unrelated area. However， in the local G coefficient， Yingkou， Dalian， Tieling are hot spots （high-high agglomeration） and Heihe is a cold spot （low-low agglomeration area）. According to the actual situation， Moran index is better than G coefficient in analyzing the spatial correlation of SO2.

Key words： spatial statistics; spatial autocorrelation; global indicators; regional indicators; GIS; SO2

空间数据包含的众多特殊性质决定了空间聚类分析研究的特殊性，本研究空间数据的空间聚类的实质，即将一组具有相关性的空间实体依据一定的相似性度量准则划分成一系列由若干空间实体构成的、具有一定意义的空间簇，同一空间簇中实体尽可能相似，不同空间簇内的实体尽可能相异[1]，以地理学第一定律为基础[2]，即空间实体之间有一定的依赖关系。空间相关性分析在功能上主要分为全局相关和局部相关，即全局指标和局部指标。全局指标（全局Moran指数、Geary系数[3]）用于探测整个研究区域的空间模式，使用单一的值来反映研究区域的自相关程度[4]。区域型指标（Morans I、局部Gearys C、全局Getiss G）用来推算空间热点（Spatial hot spot）的范围[5]。Moran指数的定义是在1950年前后，Moran[6]基于生物现象的空间分析将一维空间概念的相关系数推广到二维空间而提出。在此之后不久，Geary[7]类比于回归分析的Dyrbin-Watson统计量提出了Geary系数的概念进而逐步降低趋势;Getis等[3]于1992年提出可识别空间集聚为高值或低值聚集的全局G系数。

目前空间自相关已经广泛应用在大气污染物的研究中，程度胜[8]利用Moran指数和Gearys C对经济发展与环境污染的研究中得出了两者之间有较强的空间集聚性;徐志伟等[9]通过空间面板模型实证分析投资总量增长及结构的差异对SO2排放的影响，并用Morans指数验证，发现工业SO2的排放在部分地区形成了“高-高”聚集区域;郭梦梦等[10]采用全局Moran指数和局部Moran指数得出淮海經济区工业SO2排放存在正的空间相关性及显著的空间集聚特征。本研究以此作为切入点，以老工业基地东北三省2017年大气污染物之一的SO2为研究对象，以全局型空间自相关（Global spatial autocorrelation）、区域型空间自相关（Local spatial autocorrelation）[5]两种功用上的指标进行对比分析，探究SO2空间自相关分析中不同的衡量指标在识别空间自相关特征上的差异，为空间自相关分析提供新的思路。各指标的分析结果对大气污染物研究中空间自相关的方法运用提供了一定的参考意义，为以后研究大气污染物的空间分布状况提供了更高的可能性。

1  材料与方法

1.1  数据来源

SO2浓度数据来源于天气后报的空气质量指数查询（AQI）-PM2.5平台（www.tianqihoubao.com/aqi/）。观测内容为2017年东北三省36个地级市共169个监测站提供的日数据。

1.2  数据处理方法

1.2.1  数据整理  将监测的数据分类汇总，利用SPSS软件对原始数据分析，获得2017年东北三省2017年SO2浓度的均值，生成东北三省36个地级市的SO2等级分布（图1）。利用Stata、Geoda、Adobe Illustrator CS6、ArcGIS等软件，分析SO2的空间集聚与空间离散。

1.2.2  空间自相关分析  地理学第一定律认为，任何事物之间都是相互联系的，且相近的事物联系更为密切[2]。空间自相关是指同一个变量在不同空间位置上的相关性，是空间单元属性值聚集程度的一种度量[2，11]。目前，比较常用的衡量空间自相关的全局指标有Moran指数和Geary系数[2-4]。

本研究的空间自相关分析运用Stata软件，全局莫兰指数[12]（Morans I）的计算公式如下：

式中，I为全局Moran指数，I的取值范围为  [-1，1]，若I<0，表示空间存在负相关，越接近-1，则代表空间单元的差异越大或分布不集中;若I>0，且越是接近于1则代表空间单元关系越密切，性质也越具有相似性;若I=0，则代表区域间不相关，观测值随机分布[13]。本研究中n为36个地级市的空间数据量，yi、yj为i、j位置的空间数据的属性值，y 为SO2的均值，Wij为空间权重矩阵，表示数据i与j的相关关系，为二进制的一阶邻近空间权重矩阵，用以表示区域i与j的临近关系。

局部莫兰指数I的含义与全局莫兰指数I相似。正的Ii表示区域i的高（低）值被周围的高（低）值所包围;负的Ii则表示区域i的高（低）值被周围的低（高）值所包围。本研究采用Morans I散点图和集聚图来识别东北三省共36个地级市的SO2可能存在的局域自相关性。其公式如下：

Geary系数C与莫兰指数I不同，吉尔里系数的核心成分为（Xi-Xj）2。吉尔里系数C的取值一般介于0到2之间（2不是严格上界），大于1表示负相关，等于1表示不相关，而小于1表示正相关。Gearys C的计算公式如下：

莫兰指数I与吉尔里系数C的共同缺点为无法分别“热点”（Hot spot）与“冷点”（Cold spot）区域。所谓热点区域，即高值与低值区域;而冷点区域则是低值与低值聚集的区域。热点区域与冷点区域都表现为正自相关。为此，Getis等[3]提出了以下Getis-Order指数G。

2  结果与分析

2.1  Stata软件全局型空间自相关分析

利用公式（1）计算出2017年东北三省共36个地级市的SO2浓度的全局Moran指数I、Geary系数C，结果见表1、表2。由表1、表2可以看出，东北三省SO2浓度的全局自相关Moran指数I、Geary系数C分别为0.589、0.394。表明东北三省SO2浓度具有空间自相关性。

全局Moran指数为0.589，说明SO2在36个地级市之间存在空间自相关性，有随机产生聚类模式的可能性，Z为5.954，意味着存在正的空间自相关，即相似的观测值（高值或低值）趋于空间集聚;Geary系数C为0.394，趋于0到1之间，表明SO2存在正的空间自相关。

2.2  Geoda软件区域型功能指标空间自相关分析

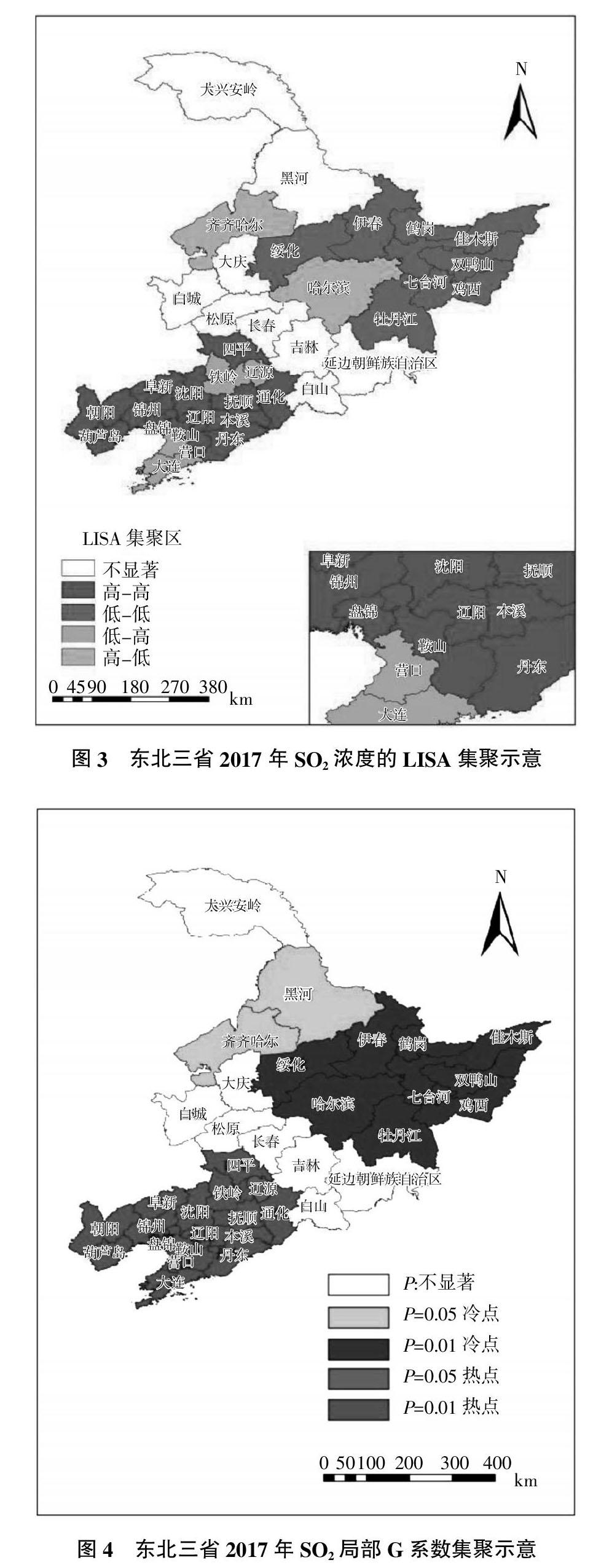
2.2.1  Moran散点图  利用Geoda软件，获得SO2的局部Moran指数绘制的散点图（图2）、LISA集聚图（图3）、G系数集聚图（图4），利用ArcGIS、Adobe Illustrator CS6等软件获得最终的图像结果。

Moran散点图的4个象限分别对应于区域单元与其邻居之间的4种类型的局部空间联系形式，且与局部Morans I相比，Moran散点图的一个重要的优势为其能够进一步具体区分区域单元与其邻居之间的4种空间形式（高值-高值、低值-低值、高值-低值、低值-高值）[4，5]。

2.2.2  LISA集聚图  图3检验结果表明，从数量上来看，2017年SO2高-高集聚区有13个，低-高集聚区有4个，低-低集聚区有8个，高-低集聚区有2个;从空间上来看，高-高集聚区主要集中在研究区的西南部，包括丹东、抚顺、辽阳、四平、盘锦、通化、本溪、鞍山、沈阳、阜新、锦州、朝阳、葫芦岛等市;低-高集聚主要集中在研究区的西南部，包括铁岭、辽源、大连、营口等市;低-低集聚主要集中在绥化、伊春、鹤岗、佳木斯、双鸭山、七台河、鸡西、牡丹江等市;高-低集聚主要集中在哈尔滨、齐齐哈尔等市。

2.2.3  G系数集聚图  利用Geoda软件获得SO2的G系数热点分析统计图用以探测区域单元的观测值在局部水平上的空间集聚程度（图4）。结果表明，辽源市的P在0.05的显著性水平上显著;四平、铁岭、抚顺、通化、本溪、丹东、辽阳、鞍山、营口、大连、盘锦、沈阳、阜新、锦州、朝阳、葫芦岛等市的P在0.01显著性水平上显著，以上17个市在空间上属于相连成片分布，由此形成SO2浓度高值与高值的空间集聚，据此可认识到这17个市趋于空间集聚的分布特征。

黑河、齐齐哈尔的P在0.05显著性水平上显著，绥化、哈尔滨、伊春、鹤岗、牡丹江、七台河、鸡西、双鸭山、佳木斯等市的P在0.01显著性水平上显著，由此可知，以上11个市之间形成SO2浓度低值与低值的空间集聚，其空间集聚的分布特征也得以显现出来。

3  小结与讨论

本研究以SO2为空间变量值，并以GIS空间统计分析技术、Adobe illustrator CS6的矢量图形软件为支撑，着重讨论全局型空间自相关（Moran指数、Geary系数）、区域型空间自相关（Morans I、局部Gearys C、Getiss G）两种指标在SO2的空间分布过程中的优劣性，克服了主观因素可能造成的偏差。研究结论如下：

1）在全局系数的讨论中，2种方法均表明东北三省SO2存在显著的空间自相关性，Moran指数表明相邻地级市的SO2浓度之间存在“趋同”现象，Gearys C表明SO2存在正的空间自相关。

2）在区域型空间自相关的研究中发现，Moran散点图、LISA集聚图、局部G系数集聚图等均揭示了东北地区36个地级市的SO2的局部空间相关性。通过分析局部Moran指数、LISA集聚图可得出低值集聚区主要集中在研究区东部，高值集聚区集中在研究区的西南部。局部G系数集聚图则得出，冷点集聚区在研究区东部方向，热点集聚区在研究区的西南部。

通过对两种指数的分析可发现，在研究区的西南部，营口、大连、铁岭3个地区的Moran指数为低-高集聚区，黑河为不相关地区，但在局部G系数中，营口、大连、铁岭为热点（高-高集聚），黑河为冷点（低-低集聚区），结合实际情况，对分析SO2空间相关性来说，Moran指数相对G系数的分析结果更优。

参考文献：

[1] 邓  敏，刘启亮，李光强，等.空间聚类及分析应用[M].北京：科学出版社，2011.

[2] TOBLER W R. A Computer movie simulating urban growth in the detroit region[J].Economic geography，1970，46：234-240.

[3] GETIS A，ORD J K. The analysis of spatial association by use of distance statistics[J].Geographical analysis，1992，24（3）：189-206.

[4] 王劲峰，李连发，葛  咏，等.地理信息空间分析的理论体系探讨[J].地理学报，2000，55（1）：92-103.

[5] 李连发，王劲峰.地理空间数据挖掘[M].北京：科学出版社，2014.

[6] MORAN P A P. The interpretation of statistical maps[J].Journal of the royal statistical society B，1948，37：24-251.

[7] GEARY R C. The contiguity ratio and statistical mapping[J]. The incorporated statistician，1954（5）：115-145.

[8] 程度胜.经济发展与环境污染相互关系的空间统计分析[D].长沙：湖南大學，2015.

[9] 徐志伟，常旭蕊.投资增长加重了中国工业二氧化硫的排放吗——基于空间面板模型的总量判断与结构比较[J].贵州财经大学学报，2016（2）：90-99.

[10] 郭梦梦，仇方道.淮海经济区工业SO2排放的空间相关性及影响因素分析[J].云南地理环境研究，2017，29（2）：33-40.

[11] GOODCHILD M. Spatial autocorrelation concepts and techniques in modern geography[M].Norwich，UK：Geo Books，1986.

[12] 陈  强.高级计量与经济学及Stata应用[M].北京：高等教育出版社，2014.

[13] 张松林，张  昆.全局空间自相关Moran指数和G系数对比研究[J].中山大学学报（自然科学版），2007（4）：93-97.

收稿日期：2018-09-20

基金项目：国家自然科学基金项目（41171412）;黑龙江省自然科学基金项目（D201303）;哈尔滨师范大学博士后项目（13RBHZ03）

作者简介：刘  梅（1993-），女，吉林榆树人，在读硕士研究生，研究方向为3S技术与地学应用，（电话）18845764579（电子信箱）LMSYei@163.com;通信作者，张冬有（1973-），男，河北清苑人，教授，硕士生导师，博士，主要从事3S技术与森林生态研究工作。