基于粒化SVM的互联网金融产品大数据回测分析
2019-07-03郜燕群
郜燕群

摘要:随着大数据时代的到来,数据挖掘技术正日益渗透到各行各业。基于数据挖掘技术挖掘出掌柜钱包的基本面数据,其目的是为了获取投资的标量信息。随后建立支持向量机的指数回归预测模型,通过模型回测判断预测效果良好。为了更好的判断未来价量信息的走向,因此采用基于模糊信息化的支持向量机指数预测模型,以每周信息为一个信息点,所得到结果准确。
关键词:大数据;信息粒化;支持向量机;指数预测
中图分类号:F23文献标识码:Adoi:10.19311/j.cnki.1672-3198.2019.16.046
1引言
“掌柜钱包”是兴业全球基金与兴业银行联合推出的互联网的理财存取业务,该业务于2014年3月10日上线运行,自上线以来在同類104只货币基金多次排前两名,截至2018年12月,资金规模达460亿元,在货币基金市场排名第五。在掌柜钱包广受欢迎的同时,我们也要对其进行预警研究,而本文使用的技术分析就是一种比较有效的方式。
技术分析注重对金融市场历史数据的研究,通过图表展现预测价格走势和投资策略分析。在理论上,技术分析只考虑市场或金融工具的实际价格行为,并认为价格会通过其他渠道反映所有投资者的相关因素。技术分析是一种证券交易的基本分析方法,也是实际操作是最大的分析方法。关于技术分析的运用和市场交易的有效性,学术界和实务界一直存在争议。但从实践角度,为了更好地理解和运用技术分析,实现投资收益,减少被动风险其研究也是非常有意义的。一个衡量风险的指标是MSE,而本文运用的SVM能够有效性的检验误差。
2文献综述
随着金融市场的扩张、金融风险预警的发展,技术分析较传统投资优势逐渐显现。Markowitz在1952年发表的《投资组合选择理论》中提出了均值-方差模型,开创了现代投资组合理论。紧接着William Sharpe 1964年对资产组合模型进行了简化,提出了资本资产定价CAPM模型,阐释了单一投资回报率与标准投资组合的投资回报率之间的相关性。随后Stephen Ross在1976年提出了套利定价APT模型,认为如果市场未达到均衡状态并且不考虑交易成本等中间因素,就会存在无风险套利机会。从而将资本资产定价理论推向了一个新的研究阶段。
近些年,机器学习技术在技术投资领域得到了快速发展,SVM作为一个常用的技术有了大量的研究。MAH Farquad 提出在解决财务问题的银行信用卡客户的流失预测和保险中的欺诈检测,SVM能够敏感性的判断,实证结果表明,所提出的改进的基于主动学习的SVM方法产生了最佳灵敏度,并且减少了规则的长度和数量,从而提高了可理解性。 L.Zhang提出SVM在供应链金融管理供应商和客户管理之间的需求,建立一个认证管理系统,从而提高了中小企业融资过程的信用评级状况。胡海清等提出了供应链金融模式下的信用风险管理,利用SVM建立风险评估体系,证实了风险评估的有效性。Hsu, Ming-Wei等提出将机器学习方法应用到金融时间序列预测上,金融市场的可预测性和基于模型的盈利交易的可行性受到市场成熟度、所采用的预测方法、预测产生的时间范围以及评估模型和模拟模型交易的方法的显著影响,且SVM预测所得到的效果显著。Shom Prasad Das等提出SVM-TLBO模型避免了用户指定的控制参数,通过预测COMDEX商品期货指数的每日收盘价来评估该混合模型的可行性和效率。实验结果表明,该模型是有效的,并且比粒子群优化(PSO)+ SVM混合和标准SVM模型表现更好。例如,与标准SVM回归相比,该模型将平均绝对误差提高了65.87%(提前1天预测),55.83%(提前3天预测)和67.03%(提前5天预测)。更多的,Johana等人分析了59篇关于SVM和金融时间序列的分析进展,结论表明SVM比传统的时间序列方法更准确。
3粒化支持向量机理论介绍
3.1相关理论
20世纪90年代初Vapnik等人根据统计学习理论提出了一种新的机器学习方法,即SVM方法。该方法以结构风险最小化原则为理论基础,通过适当地选择函数子集及该子集中的判别函数,使学习机器的实际风险达到最小,保证了通过有限训练样本得到的小误差分类器,对独立测试集的测试误差仍然较小。在支持向量和输入空间抽取的向量之间的内积核是构造支持向量机学习算法的关键。其中支持向量机是由算法从训练数据中抽取的小子集构成。其种类主要有:
线性核函数:K(x,xi)=xTxi ;
多项式核函数:K(x,xi)=(γxTxi+r)p,γ>0;
径向基核函数:K(x,xi)=exp(-γ||x-xi||2),γ>0;
两层感知器核函数:K(x,xi)=tanh(γxTxi+r)
通过对比发现,虽然对掌柜钱包进行了回归预测,但是大多数时候无法对指数进行精确预测,如果能够对开盘指数和变化空间进行预测就显得很重要。利用SVM对进行模糊信息粒化后的每日开盘指数进行变化趋势和变化空间的预测。
信息粒化由美国数学家Lotfi A.Zahdeh 教授提出,是粒化计算和词语计算的主要方面,研究信息粒化的形成、表示、粗细、语义解释等。从本质上讲,信息粒化是通过不可区分性、相似性、功能相近性、函数性等来划分对象的集合。是将一个整体分解为一个个相似的元素部分进行研究,每个部分为一个信息粒。这种信息粒命题表达方式为:
gΔ-xisGisλ 或者gΔ-xisG
其中x是论域U中取值的变量,G是U的模糊子集,由隶属函数μG来刻画。λ表示可能性概率。一般假设U为实数集合RR'',G是U的凸模糊子集,λ是单位区间的模糊子集。
3.2“掌柜钱包”技术分析模型构建
选取数据:每一行表示每一个交易日的掌柜钱包指数各种指标,6列分别表示当天指数的开盘指数,指数最高,指数最低值,收盘指数,当日交易量,当日交易额。
模型目的:利用SVM建立的回归模型对指数每日的开盘数进行回归拟合
模型假设:指数每日的开盘数与前一日的开盘指数,指数最高值,指数最低价,收盘指数,交易量和交易额相关,即把前一日的开盘指数,指数最高值,指数最低价,收盘指数,交易量和交易额作为当日开盘指数的自变量,当日的开盘指数为因变量。
在给定的训练样本x1,y1,...,xn,yn,i=1,2,...,n,采用不敏感损失函数算法,寻找回归函数f(x,α)=wx+b中的参数w,b,将问题转化为:
min12w2+C∑ni=1ξi+ξ*i
s.t.(wxi+b)-yiSymbolcB@
ε+ξiyi-(wTxi+b)SymbolcB@
ε+ξ*iξi,ξ*i0,i=1,2...n
引入拉格朗日函數可以得到对偶规划
min12∑ni,j=1α*i-αiα*j-αjxixj+ε∑ni=1α*i+αi∑nj=1yiα*j-αj
s.t.∑ni=1(α*i-αi)=00SymbolcB@
αi,α*iSymbolcB@
C,i=1,2...n
对于非线性回归类似,可以通过核函数来实现。
目前比较常用的核函数类型有:
线性核函数:K(x,xi)=xTxi ;
多项式核函数:K(x,xi)=(gxTxi+r)d;
高斯核函数:K(x,xi)=exp(-g‖x-xi‖2) ;
Sigmoid核函数:K(x,xi)=tanh(gxTxi+r)
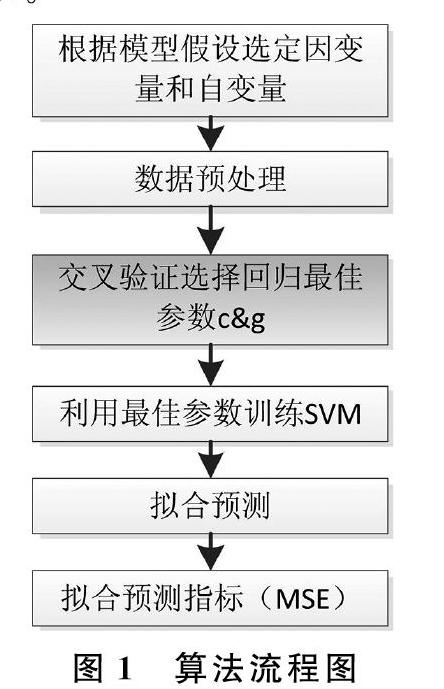
支持向量机的核函数以及参数的选取对其目标的预测性能有很大的影响,从现有的研究成果来看,大多数情况下最常用的核函数-高斯核函数都获得了较好的预测效果,因此本文借鉴已有的研究成果采用高斯核函数进行研究。此时的支持向量机存在两个需要调节的参数:惩罚参数c和高斯核函数参数g。上述算法流程如图1所示。
对于掌柜钱包的有效预测可以从整体上观测股市的变化提供强有力的信息,所有对掌柜钱包的预测很有意义,通过对掌柜钱包的开盘至今的每日开盘数据进行回归分析。
4结果分析
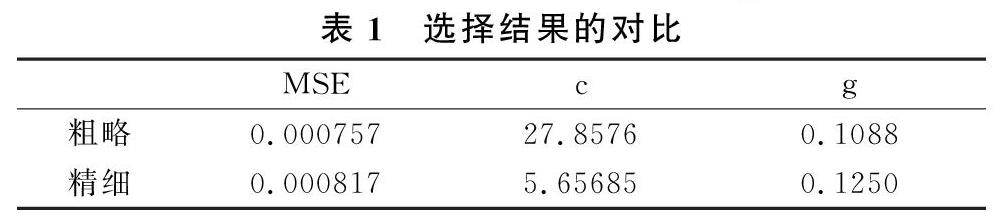
通过使用核函数-高斯核函数的研究网络搜索法来对高斯核函数g和惩罚参数c进行优化选择实现。选择回归预测分析最佳的SVM参数c&g。
利用上面得到的最佳参数c和g对SVM进行训练,然后再对原始数据进行回归预测,得出图1、图2。利用回归预测分析最佳的参数进行SVM网络训练。
利用网格搜索法最终得到的拟合结果为:均方误差MSE=0.000362,相关系数R = 98.56%,在95%的置信区间下,预测的准确率为93.98%,预测效果良好。利用高斯核函数的强大回归,得到的效果良好。
对上一个模型进行改良的上面是对一个指标进行回归预测,而这里进行的是对3个指标(最低价,平均价,最高价)进行回归预测,得到的是一个区间进行说明,其准确性更高。
利用SVM对模糊粒子Low进行回归预测。基于上面寻得的参数,利用支持向量机回归预测。
对于Low的拟合结果分析,利用上面得到的最佳参数训练和预测,最终Low模型得到的拟合效果为:
均方误差MSE=0.0045
相关系数R =85.90%
接下来5个交易日的平均模糊粒子参数:
predict_low =1.3321
再次利用SVM对R、Low进行回归预测。最终结果如下,求得的模糊粒子参数最低值Low,平均值r,最高值Up的预测值分别是:
[Low,R,Up]=[1.3321, 13652, 1.4022]
通过与接下来的几天进行实证分析其结果确实是在里面,证明回测成功。通过截取2019年1月2-4日的K线图,可以证明拟合效果良好。
5结论及未来工作
在粒化SVM建模回测过程中没有考虑手续费和冲击成本等因素,仅仅是一个大概的测试结果,其目的是为了说明使用SVM交易策略建模的思想和过程。本节提出的模型也可以扩展到小时级别,分钟级别等其他频率交易数据模型的构建。
虽然技术投资分析在我国尚处于发展起步阶段,但2010年以来发展态势快速,未来发展前景广阔。近些年来机器学习的大力发展也为金融技术投资分析提供了理论基础,也让技术投资不失为一种非常高效的金融分析方法。值得注意的是,虽然技术投资是一种客观、高效、无偏的投资方式,但投资者也不能过度依赖,毕竟市场的多变性和有效性都会给技术投资带来诸多挑战,因而需要充分发挥金融工程师的创造力,不断挖掘创新投资模型。相信随着大数据技术、人工智能的快速发展,技术投资在国内会有更好的发展势头。
参考文献
[1]Kamla Ali Al-Busaidi.Aligning customer knowledge management tools with business strategy[J].International Journal of Electronic Customer Relationship Management, 2013,(7):2,117-134.
[2]Markowitz H.Portfolioselection[J].The journal of finance, 1952, 7(1):77-91.
[3]Sharp, W.F., Capital asset prices: A theory of market equilibrium under condition ofrisk[J].Journal of Financial Economics, 1964,19(3):425-442.
[4]Cox J C, Ross S A.The valuation of options for alternative stochasticprocesses[J].Journal of financial economics, 1976, 3(1-2): 145-166.
[5]Zhang L, Hu H, Zhang D.A credit risk assessment model based on SVM for small and medium enterprises in supply chainfinance[J].Financial Innovation, 2015, 1(1):14.
[6]胡海青,張琅,张道宏,陈亮.基于支持向量机的供应链金融信用风险评估研究[J].软科学,2011,25(05):26-30+36.
[7]Hsu M W,Lessmann S, Sung M C, et al.Bridging the divide in financial market forecasting: machine learners vs.financial economists[J].Expert Systems with Applications, 2016, (61): 215-234.
[8]Jaramillo J, Velasquez J D, Franco C J.Research in financial time series forecasting with SVM: Contributions from literature[J].IEEE Latin America Transactions, 2017, 15(1):145-153.
[9]Das S P,Padhy S.A novel hybrid model using teaching–learning-based optimization and a support vector machine for commodity futures index forecasting[J].International Journal of Machine Learning and Cybernetics, 2018, 9(1): 97-111.
[10]张卫国,卢媛媛,刘勇军.基于非均衡模糊近似支持向量机的P2P网贷借款人信用风险评估及应用[J].系统工程理论与实践,2018,38(10):2466-2478.
[11]Schumakerrp,Chenh.Textual analysis of stock market prediction using breaking financial news[J].The Journal of Finance,2009:5-19.
[12]Chih-Chung Chang and Chih-Jen Lin.LIBSVM: A Library for Support Vector Machines[EB/OL].http://www.csie.ntu.edu.tw/~cjlin/papers/libsvm.pdf, 2013.
[13]Chao-Ton Su, Long-Sheng Chen,Yuehwern Yih.Knowledge acquisition through information granulation for imbalanced data[J].Expert Systems with Applications, 2006,(31):531-541.
[14]J.Bollen,H.Mao and X.Zeng.Twitter mood predicts the stock market[J].Journal of Computational Science, 2011,(2):1-8.
