立体几何强化训练B卷
2019-07-03张红莉
张红莉


一、选择题
1.关于斜二测画法画水平放置的图形的直观图,下列描述不正确的是()。
A.三角形的直观图仍然是一个三角形
B.90°的角的直观图会变为45°的角
C.与y轴平行的线段长度变为原来的一半
D.原来平行的线段仍然平行
2.下列命题中正确的是()。
A.正方形的直观图是正方形
B.平行四边形的直观图是平行四边形
C.有两个面平行,其余各面都是平行四边形的几何体叫棱柱
D.用一个平面去截棱锥,底面与截面之间的部分组成的几何体叫棱台
3.如图1,在△ABC中,∠ACB=90°,直线l过点A且垂直于平面ABC,动点P∈l,当点P逐渐远离点A时,∠PCB()。
A.变大
B.变小
C.不变
D.有时变大有时变小
4.已知二面角a-AB-β的平面角是锐角,C是平面a内一点(它不在棱AB上),点D是点C在面β上的射影,點E是棱AB上满足∠CEB为锐角的任一点,那么()。
A.∠CEB>∠DEB
B.∠CEB=DEB
C.∠CEB<∠DEB
D.∠CEB与∠DEB的大小关系不能确定
5.已知A,B,C三点不在同一条直线上,0是平面ABC内一定点,P是△ABC内的一动点,若λ∈[0,+∞),则直线AP-定过△ABC的()。
A.重心
B.垂心
C.外心
D.内心
6.点O,I,H,G分别为△ABC(非直角三角形)的外心、内心、垂心和重心,给出下列关系式:
①GA+GB+GC=0;②sin2A·0A+sin2B·B+sin2C·oC=0;③aIA+bB+cC=0;④tanA·HA+tanB·HB+tanC·HC=0。其中一定正确的个数是()。
A.1
B.2
C.3
D.4
7.三棱锥P-ABC的高为h,且此棱锥的内切球的半径r=1/7h,则=()。
A.
B.
C.
D.
8.图2所示的是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为()。
A.20π
B.24π
C.28π
D.32π
9.在正方体ABCD-A1B1C1D1中(如图3),已知点P在直线BC1上运动,有下列四个命题:①三棱锥A-D1BC的体积不变;②②直线AP与平面ACD,所成的角的大小不变;③二面角P-ADC的大小不变;④M是平面A.B,CiD]内到点D和C1距离相等的点,则M点的轨迹是直线AD。其中正确命题的编号是()。
A.①③④
B.①②
C.①③
D.①④
10.已知四边形ABCD,AB=2BC,把这个矩形分别以AB,BC所在直线为轴旋转一周,所成几何体的侧面积分别记为Sq,Sz,则Sn与S2的比值等于()。
A.
B.1
C.2
D.4
11.在四棱锥P-ABCD中,PO⊥平面ABCD,E为线段AP的中点,底面ABCD为菱形,如图4所示。若BD=2,PC=4,则异面直线DE与PC所成角的余弦值为()。
A.
B.
C.
D.
12.如图5所示,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面ABCD为菱形,M是PC上的一个动点,若要使得平面MBD⊥平面PCD,则应补充的个条件可以是()。
A.MD⊥MB
B.MD⊥PC
C.AB⊥AD
D.M是棱PC的中点
二、填空题
13.已知平面x//β,A,C∈anB,D∈β,直线AB与CD交于Sn若AS=18,BS=9,CD=34,则CS=____。
14.在三棱锥P-ABC中,平面PAC⊥平面ABC,AB⊥BC,△PAC为等边三角形,若AB=BC=2/3,则三棱锥P-ABC的外接球的体积为____。
15.已知棱长为36的正四面体A-BCD的内切球球面上有一动点M,则MB+1/3MC的最小值为____。
16.如图6,在正方体ABCD-A.B:C.D、中,M,N分别为棱C:D,C.C的中点,有以下四个结论:①直线AM与CC1是相交直线;②直线AM与BN是平行直线;③直线BN与MB,是异面直线;④直线AM与DD1是异面直线。其中正确的结论为____(把你认为正确的结论的序号都填上)。
三、解答题
17.如图7,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点,△PAD是正三角形。
(1)求证:AD⊥平面PQB;
(2)已知点M是线段PC上,MC=λPM,且PA//平面MQB,求实数λ的值。
18.如图8,在三棱锥S-ABC中,侧面SAC与底面ABC垂直,E,0分别是SC,AC的中点,SA=SC=:2,BC=.AC,∠ASC=∠ACB=90°。
(1)求证:OE//平面SAB;
(2)若F是线段BC上的任意一点,求证:OE⊥SF;
(3)求三棱锥S-ABC的体积。
19.如图9所示的圆锥的体积为,底面直径AB=2,C是AB的中点,D是母线PA的中点。
(1)求该圆锥的侧面积;
(2)求异面直线PB与CD所成角的大小。
20.如图10,在直三棱柱中,AD⊥平面ABC,其垂足D落在直线A1B上。
(1)求证:BC⊥A1B;
(2)若AD=,AB=BC=2,P为AC的中点,求直线PC与面PA.B所成角的余弦值。
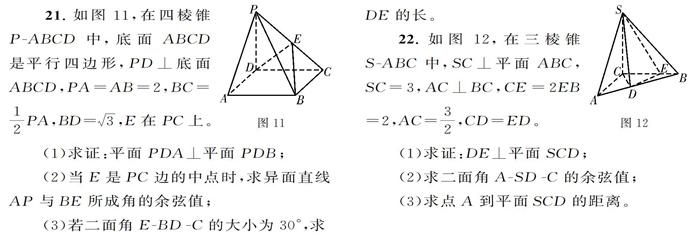
21.如图11,在四棱锥P-ABCD中,底面ABCD是平行四边形,PD上底面ABCD,PA=AB=2,BC=2PA,BD=v3,E在PC上。
(1)求证:平面PDA⊥平面PDB;
(2)当E是PC边的中点时,求异面直线AP与BE所成角的余弦值;
(3)若二面角E-BD-C的大小为30°,求DE的长。
22.如图12,在三棱锥S-ABC中,SC⊥平面ABC,SC=3,AC⊥BC,CE=2EB=2,AC=,CD=ED。
(1)求证:DE⊥平面SCD;
(2)求二面角A-SD-C的余弦值;
(3)求点A到平面SCD的距离。
