由一道习题引发的教学改进始末

吴晓雄

【摘要】解决百分数实际问题一直以来是教学中的一个难点，本文叙述了从一次不经意间的个别辅导，引发了暴露错误、放大错误、经历错误直至改正错误的一次教学改进行动，这样的教学改进行动给了我们很多的启示。

【关键词】缘起 测试 原因分析 行动 实践再反思

一、缘起

六年级进入单元复习阶段，在一次复习测试中，完成下面这道有关百分数问题的题目时，有一个学生遇到困难，对笔者说这道题不会做：

青云小学下半年用水量比上半年少20%，上半年用水量占全年用水量的几分之几？

为了了解学生的真实想法，笔者与这名学牛进行了交流，部分交流记录如下（T为老师，S为学生）：

T：这道题你不会做，你能说说为什么吗？

S：我想求出全年的用水量，没法求。

T：你为什么要求出全年的用水量？

S：因为上半年的用水量和全年的用水量都知道了，就能求出上半年用水量占全年用水量的几分之几。

T：你为什么没法求出全年的用水量？

S：因为上半年和下半年的用水量都不知道，没法求。

T：这道题的单位“1”是什么？

S：这个我知道，是上半年的用水量。

这个学生面对这道题束手无策，那么，班中其他学生面对这道题，是否也存在困难？为了了解学生解决这道题的情况，笔者安排了一次题量不多的专项测试。

二、测试

这次测试内容，均为百分数知识的习题。试题编制形式既有填空题，也有应用题。对象为笔者学校六年级的两个平行班。其中，在填空题中，笔者安排了这些习题（以下为测试卷的部分习题）：

1.学校图书馆中，科技书比故事书多25%，故事书比科技书少（ ）%。

2.数a与数b的比是4：5，那么a是b的（ ）%，b比a多（ ）%。

3.甲数是乙数的4/5，乙数比甲数多（）%，甲数比乙数少（ ）%。

4. 一件商品打九折后，又提价l0%，现在的价格是原来价格的（ ）%。

5.小圆面积是大圆的20%，那么小圆面积和大圆面积的最简整数比是（ ）。

为了解学生在解决上述问题时的思考过程和采用的解决方法，在这张测试卷的末尾，笔者特意安排了这样一道题：

填空第1题和第3题的答案，你是怎么思考的？请把你思考的过程写在这张测试卷的下面（用文字、算式或者线段图等都可以）。

第1题：

第3题：

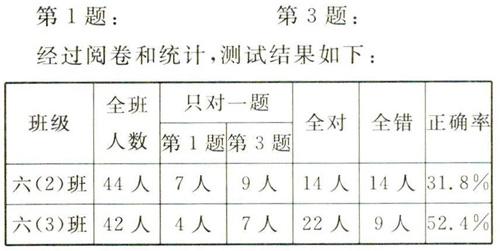
三、原因分析

从测试的结果分析，针对这两道题，两个班级的成绩有一定的差距，六（3）班明显好于六（2）班，这两个班级由同一位教师授课，通过对教师的访谈知道这两个班本来数学基础有差异，这样的结果在情理之中。但这样的测试汇总结果，让笔者不由陷入了思考，究竟是什么原因导致学生在面对这砦题时思维受阻，无从下手呢？问题到底出在哪？是教师教的问题还是学生学的问题？测试结束后，笔者在未对试卷进行讲评前，访谈了部分存在解答困难的学生。

T：解答这道题时，你是怎样想的？

Sl：我觉得科技书比故事书多25%.故事书就比科技书少25%。

T：为什么呢？

Sl：因为科技书比故事书多25本的话，故事书就比科技书少25本。

T：解答这道题时你是怎样想的？

S2：甲数可以看作4，乙数可以看作5。

T：如果这里告诉你的不是分数，是百分数，你还能算出甲数看作几吗？

S2：可以。

T：怎么算呢？

S2：把这个百分数转化成分数，就是几分之几了。

T：要计算甲比乙少百分之几，应该怎么算？

S2：4÷5=80%、

T：为什么这样算？

S2：用甲数除以乙数就行了。

从上面的访谈里，可以探寻出学生缘何无法正确、顺利地解决問题的根源来。

1.理解不透：分数意义的掌握还欠透彻

分数关系是刻画几个数量关系之间的又一种方式，有别于整数关系的是，它以其中一个数量作为比较的标准，能更灵活、细致、准确地表示各部分量之间的关系，与高年级“比”“百分数”等数学知识联系十分紧密。有专家指出：“分数概念的获得，使儿童对数的理解有了一个突破性的进展，这为他们进一步学习数学，用数学来解决实际问题提供了有力的保证。”理解、掌握分数的意义，能有效地培养、提高学生的逻辑思维能力，促进学生数学知识系统的逐步完善。可见，五年级的“分数的意义”，是学生学习并解决测试卷中这类习题的重要知识基础。借用奥苏伯尔的学习准备原理来说，分数（百分数）意义的相关知识，是解决这类习题的认知准备。对于“甲数是乙数的4/5，乙数比甲数多（ ）%，甲数比乙数少（ ）%”来说，对于，4/5意义的理解越深刻、透彻，越有利于学生对这个问题的解决。存在解决障碍的学生，因为对分数意义的理解不深刻，无法顺利提取相关的知识储备，对数的认识还不能从具体数量过渡到对关系的考虑上，所以学生对这类没有具体数量的计算显得力不从心。在本次测试卷中，同样的含有具体数量的习题，学生完成情况就普遍好于第1、3两题。

书法兴趣小组有女生l6人，男生人数比女生人数多25%，女生占书法兴趣小组全部人数的几分之几？

题中“男生比女生多25%”的条件与第4题是一致的，但因为有“女生16人”这个具体数量的存在，所以学生很容易计算女生占法兴趣小组的4/9。从与学生的访淡中可以印证这一点，从正确解答的学生身上也可以印证这一点。

2.方法不足：问题解决的策略缺乏指导

在平时的教学中，对“一件上衣，原价200元，现在降价l/5，现在售价多少元？”“食堂运来120千克面粉，是运来的大米的40%，面粉和大米一共运来多少千克”这类问题的教学，教师所花的精力和时间比较多，理解题意，确定方法等分析过程细致、具体，但对本文所述的这种习题，欠缺解决方法的指导.缺少对学生如何正确解答这些问题的思考过程的关注和分析。无法正确解答的学生如何思考并解决这类问题？测试卷上学生给出了这些解决方法（如图）：

可见，解题的策略与分析问题的思考方法的应用在这个问题的解决过程中起着极为重要的作用。学生对策略应用的女好坏，对“求一个数比另一个数多（或少）百分之几”应用题分析的正确与否，直接影响着他对于问题的解决。这也正是本类习题在这次测试中解答成功与否的又一重要原因。

四、行动

有了以上的认识与分析，笔者对这部分百分数应用问题进行了课堂练习设汁，并进行了教学改进实践。

第一步：联系中复习

①学校羽毛球队共有20人，其中男生12人，女生人数是男生的（ ）/（ ），男生比女生多（ ）%。

②学校乒乓球队男生人数占全队人数的3/5，男生人数与女生人数的最简整数比是（ ）：（ ）。男生人数是女生人数的（ ）/（ ），男生比女生多（ ）%。

学生自主完成，课堂交流填空结果。问：要求男生人数是女生的几分之几，可以怎样汁算？男生人数比女生多百分之几，可以怎样计算？

小结得出：求一个数是另一个数的百分之几，可以用“一个数÷另一个数（单位‘1）=百分之几”进行计算;一个数比另一个数多（少）百分之几，可以用“两数相差数÷另一个数（单位‘1）=多（少）百分之几”进行计算。

第二步：课堂重点练习

（l）对比练习。

①学校田径队有男生lO人，女生比男生多20%，男生占田径队总人数的几分之几？

②学校田径队中女生比男生多20%，男生占田径队总人数的几分之几？

课堂重点反馈第②题的解答方法：

方法1：画线段图（略）。

方法2：把男生看作100人，女生就是100×（1+ 20%）=l20人了。这样就能算出男生占田径队总人数的几分之几。

方法3：我把男生人数看作单位“1”，女生人数就是l+20%=1.2，l÷（1.2+1），也能算出男生占径队总人数的几分之几。

方法4：我把20%化简成分数是1/5，男生人数可以看作5，女生人数就是6，也能算出男生占田径队总人数的几分之几。

师：通过计算，你认为这两道题的题目一样吗？（生有的说一样，有的说不一样）请你说一说：相同的地方在哪里，不同之处又在哪里？这两道题的解法一样吗？它们相同的地方在哪里，不同之处又在哪里？遇到没有具体数量的题可以怎样想？这些方法中你最喜炊哪种方法？为什么？

（2）回顾应用。

你能用上刚才同学们介绍的解答方法，完成并订正上面这些习题吗？

方法总结：呈现并提炼出解答方法。

（3）错例分析。

（课堂呈现测试卷上的错题）他们这样思考对吗？请你说说错的原因。

第三步：方法巩固

（l）填空：大圆周长是小圆周长的l20）%，小圆，周长与大圆周长的最简整数比是（ ）：（ ），大圆周长比小圆周长长（ ）%。。

（2）判断：甲数比乙数少1/3，甲数与乙数的比是4：3。（ ）

（3）选择：大圆的面积比小圆的面积大l/5，那么，小圆的面积比大圆的面积小（ ）。

A.1/5

B.1/6

C.1/4

这三步举措，主要基于如下思考：

l.迁移中联系旧知

众所周知，分数、百分数、比和除法之间的联系十分紧密，但学生的思维特点仍处在由形象思维向抽象思维不断过渡的过程中。在上述教学中，考虑到学生需要具体数量参与才能正确进行计算的表现和思维特点，笔者把问题解决的起点，设定在复习分数的意义、百分数与比的关系等旧知中，通过练习迁移旧知，沟通并强化三者之间的联系;把释疑解困的教学干预的着力点，集中在既有聯系又有区别的对比练习上。通过这个对比练习，学生得以明确：

①既可以根据具体数量来解决问题.也可以根据几个量之间的关系来解决问题。

②如果没有具体数量，可以采用其他办法，根据这几个量之间的关系也能解决“一个数是另一个数的几分之几”“一个数比另一个数多（少）百分之几”等问题。

③分数、百分数和比都能表示出几个量之间的关系，这三者之间也可以相互转化。

2.共享中习得方法

从试卷上学生给出的解决方法不难看出，学生的想法是多样的。这些源于学生且闪现着学生智慧火花的方法，正是解决这类问题的典型、有效、易于理解的方法。有位哲人说：“你有一个苹果，我有一个苹果，交换后每人还是一个苹果;你有一种思想，我有一种思想，交换后每人有两种思想。”对这些方法的课堂展示、共享与交流反馈，在引导学生改正错误的同时，增进了对比、百分数和分数的理解，更重要的是，丰富了这一类问题的解决策略。

3.练习中形成技能

紧随其后的练习，则重在帮助学生巩固所学方法，引导学生懂得习得方法后的应用与反思。既有对测试题思考过程的回顾，也有对前面所学的他人新方法的应用，更有对这些错例的错因所在而进行的分析与反思。在这样回顾—应用—纠错—练习的过程里，解决方法的提炼水到渠成：可以画图计算，也可以假设举例，还可以应用关系进行解答。

五、实践再反思

俯下身来才能察觉学生的思维视角。一次不经意间的个别辅导，引发了暴露错误、放大错误、经历错误直至改正错误的一次教学改进行动。本文开头的学生，经后续了解，她已经掌握了用多种计算方法来解决此类问题。