基于改进自适应小生境遗传算法的机械臂逆运动学求解

杨惠珍, 刘西洋

(1.西北工业大学 航海学院, 陕西 西安 710072; 2.水下信息与控制重点实验室, 陕西 西安 710072)

机械臂轨迹规划和位姿控制的关键问题之一是逆运动学求解,即由机械臂末端抓手位姿矩阵求所需关节角矩阵。逆运动学是笛卡尔空间到关节空间的一种复杂非线性映射关系,通常具有多个解,如何从解集中选取出所需的最优解也是机械臂轨迹和位姿控制需要解决的难点之一。

机械臂逆运动学求解的传统方法包括:解析法,几何法和数值法等[1]。针对不同款六自由度工业机械臂,Kucuk等[2]将数值法与解析法结合,求得了封闭解;Liu等[3]提出矩阵分块化简的解析法,解决了逆运动学的奇异性问题,并以PUMA560为对象进行了验证;对于具有冗余关节的机械臂,Pfurner[4]利用数值解法求得了完整封闭解;魏延辉等[5]采用构形平面法将机械臂工作构形进行位置和姿态匹配,然后采用半解析的方式求得逆运动学解,解决了奇异解问题;徐文福等[6]提出了逆运动学求解的关节角参数化及臂型角参数化2种方法,求得了解析解,并通过仿真算例对所提算法进行了有效性校验。Tørdal等[7]采用共形几何代数法求得了其解析解,为逆运动学求解提供了一种新方法。

在数值法研究方面,有学者利用神经网络算法来求解机械臂的逆运动学问题。Almusawi等[8]采用人工神经网络算法,Köker[9]采用模拟退火算法优化的神经网络算法,Yuan等[10]提出误差逆传播(BP)与径向基(RBF)并行的神经网络算法,解决机械臂求逆问题。神经网络算法通过正运动学获取训练及测试数据,将位姿矩阵和关节角矩阵分别作为网络的输入和输出,建立两者的映射关系,完成求逆运算。然而上述文献中,运用神经网络建立逆运动学模型时对训练样本进行了限制,使其成为单解问题,因此可以得到收敛的最优解。机械臂运动学是笛卡尔空间与关节空间之间的非一对一映射关系,训练样本应尽可能代表机械臂工作空间。利用神经网络算法无法对这种非一对一的映射关系进行准确建模,求解逆运动学时存在缺陷。

逆运动学是一个多元多峰函数最值求取问题,遗传算法(genetic algorithm,GA)等智能优化算法也可用于求解该类问题。Çavdar[11]提出了基于人工蜂群的逆运动学求解算法,并与粒子群算法,和谐搜索算法进行了对比分析。Huang等[12]基于混合Taguchi DNA群体智能算法对逆运动学进行了求解,并与GA进行了精度对比。Tabandeh等[13]通过自适应小生境遗传算法(adaptive niched genetic algorithms,ANGA)对逆运动学问题进行了分析,求得了六自由度机械臂的8组逆解。智能优化算法在解决逆运动学问题时以最小化位姿误差为目标,对机械臂构型无特殊要求,通用性强。

本文对基于ANGA的逆运动学求解方法进行了研究,主要做了以下几点改进:(1)提出了融合位姿误差和“最柔顺”原则的适应度函数,求得了最柔顺即能耗最小的最优解。(2)引入减法聚类算法解决ANGA需准确已知逆解个数的限制,提升了算法通用性。(3)遗传算法的选择算子采用最优保存策略,交叉操作基于君主方案,进行多点非均匀变异,提升算法的收敛速度及精度。

1 机械臂运动学求解问题

根据Denavit和Hartenberg提出的D-H法,连杆坐标系i和坐标系i-1之间的关系由以下4个变量进行描述:关节角θi、连杆扭角αi-1、连杆偏移di、连杆长度ai-1,可得连杆坐标系和坐标系之间的齐次变换矩阵如(1)式所示

(1)

式中,c代表角度余弦,s代表角度正弦。θi,αi-1,di,ai-1即D-H参数,由机械臂的结构决定。

对于n自由度的机械臂来说,正运动学是由关节角矩阵求位姿矩阵0Tn的过程,如(2)式所示。

(2)

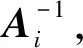
2 遗传算法适应度函数

适应度值是GA 选择优良个体的衡量标准,被选中个体完成后续的交叉、变异操作。适应度函数常由目标函数变换而来,用以计算个体的适应度值。

2.1 基本适应度函数

为了保证机械臂达到期望位姿的误差最小,目标函数选为个体位姿与期望位姿之间的误差

f(P,O)=min(ωpPe+ωoOe)

(3)

式中,Pe表示位置误差,Oe表示姿态误差。位置误差用欧氏距离来计算

(4)

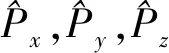
姿态误差用横滚,俯仰和偏转角RPY各角度差值的绝对值之和来表示

Oe=|(R-φ)|+|(P-θ)|+|(Y-φ)|

(5)

式中：R,P,Y分别代表期望点的横滚角、俯仰角和偏转角；φ,θ,φ代表GA中个体的横滚角、俯仰角和偏转角。由于位置与姿态误差描述所采用的单位不同,因此在两者叠加时需进行归一化操作,归一化系数ωp和ωo如(6)～(7)式所示

(6)

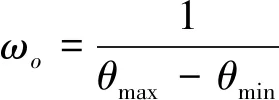
(7)

式中：Pmax为机械臂所能达到的最大工作距离；θmax和θmin分别为关节工作范围的最大最小值。

对于逆运动学求解,(3)式所得结果越小,代表该个体具有更高的求解精度,其更应被遗传算法选中。因此,适应度函数定义为

(8)

2.2 融合“最柔顺”原则的适应度函数

“最柔顺”原则即机械臂从当前位姿点到期望点之间各关节转角之和尽量小,大臂运动尽量少,因此建立如下的目标函数

(9)

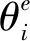
将最柔顺目标与位姿目标相结合,构建目标函数及适应度函数分别如下所示

f(P,O,θ)=γf(P,O)+(1-γ)f(θ)

(10)

γ=0.5·e-f(P,O)+0.5

(11)

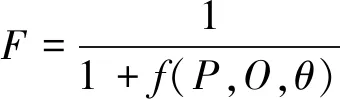
(12)

γ是位、姿误差动态权重值,用于调节进化方向。遗传进化开始时,f(P,O)较大,γ接近于0.5。随着个体的进化,f(P,O)逐渐减小,γ向1靠近。适应度函数如此设置,可使f(P,O)与f(θ)在进化过程中占有合适的权重,使得进化方向更加合理。

3 基于改进自适应小生境遗传算法的逆运动学求解

3.1 自适应小生境遗传算法

小生境遗传算法(niched genetic algorithms,NGA)可以更好地保持解的多样性,同时具有更好的全局寻优能力和收敛速度,特别适合于复杂多峰函数的最值求取问题[14]。NGA在解决多峰函数的最值求取问题时,需准确设定小生境半径dmin,对逆运动学求解而言,dmin无法准确获得。由Goldberg和Wang提出的ANGA基于经济学的垄断竞争模型[15],将个体分为商家和顾客两大群体,商家以最大化小生境半径范围内顾客数量且更接近其他商家为目标,顾客以最接近商家而又最不拥挤为目标,通过两者的共同进化实现多峰问题求解。ANGA的小生境半径由个体间欧氏距离确定,而后逐步更新,并依群体进化目标自适应调整。对于逆运动学求解来说,商家就是最优关节角组合的代表,顾客则是遗传算法迭代操作的个体。

3.2 自适应小生境遗传算法改进

ANGA在求解多峰函数问题时,需通过先验知识准确设定商家个数。由于仅通过正运动学无法推知逆解个数,故引入聚类算法对ANGA运算结果进行聚类分析。本文采用减法聚类算法。减法聚类是根据周围数据点的密度寻找最佳数据点以定义聚类质心的方法,通过聚类分析使得利用改进ANGA求逆时无需准确设定逆解个数。其参数设定在下述步骤9中详细说明。

遗传算子的设定对GA的收敛速度及搜索能力具有决定性作用。标准遗传算法的选择操作基于“轮盘赌”法,依概率对个体进行选择,存在一定的随机性,会使部分优良个体缺失,选择误差较大。本文选择算子采用最优保存策略,即个体依适应度值高低进行排序,选取适应度值高的一半个体作为父代,进行交叉、变异操作产生子代,更利于优良个体信息的保持,提升算法的收敛速度及精度。交叉操作采用君主方案,即取最优个体与所有偶数位个体进行交叉操作产生新个体,使得新个体都含有最优个体部分信息,使得进化更具方向性;变异操作基于非均匀多点变异,与均匀变异相比能够增强重点区域的局部搜索能力,改善标准遗传算法局部搜索能力差的问题。

3.3 改进ANGA算法流程

Step 1 构建种群:随机产生相互独立的商家和顾客种群,每个个体都由n个关节角度值组成。

B=[θ1,θ2,…,θn]T

(13)

C=[θ1,θ2,…,θn]T

(14)

式中,B和C分别代表商家和顾客种群,每个关节角度值在其工作范围内随机产生。对于个体θi=[θi1,θi2,…,θim],用欧式距离来衡量个体间差距。

dij=‖θi-θj‖i,j=1,2,…,m

(15)

Step 2 计算小生境半径(dmin):dmin与适应度值及评定新商家是否更优相关,初值常由(17)式计算而得

(16)

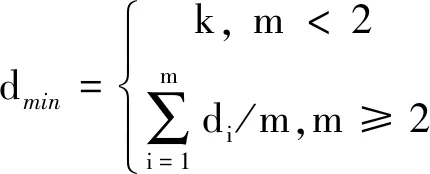
(17)

式中,di为个体i与其他个体之间的最小欧式距离,m为个体总数,k通常取1。对于满足dij≤dmin的个体,将其加入到对应的小生境群体中。

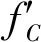
(18)

式中,fC依(8)式或(12)式计算而得,CB代表商家B所服务的顾客的集合。简而言之,同一小生境范围内的顾客共享适应度值。

商家的适应度值是其所服务顾客适应度值的总和

(19)

Step 5 交叉、变异操作:交叉操作采用君主方案,从父群体中选取最优个体与其他所有偶数位的个体进行交叉,产生新群体;完成交叉操作后,进行非均匀多点变异操作,产生子群体。

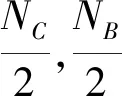
Step 7 更新小生境半径(dmin):dmin初值取di的平均值可尽量多地包含个体,保证小生境系统的多样性。迭代过程中,应逐渐减小dmin。随着dmin的减小,顾客集中区域的商家仍保有顾客,而分散区域的商家将被迫寻找顾客集中度更高的区域,使最终结果更为接近最优解。在每步迭代中,dmin按照(20)式逐步较小

(20)

式中,G为最大迭代步数,Gt为当前迭代步数,λ通常取0.2～0.8之间的常数。

Step 8 终止判定:判定适应度值是否小于设定误差范围或迭代次数是否已满足要求,若是则退出循环输出结果,否则返回步骤5,继续循环。

Step 9 减法聚类分析:减法聚类将聚类中心数据集中的每个点都视作潜在的聚类中心,根据周围数据集密度指定聚类中心。对于M维的数据集{x1,x2,…,xn},样本xi的密度值为

(21)

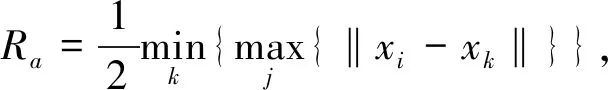
选取数据集中密度值最高的点xc1作为第一个聚类中心。假定xck为第k次选定的聚类中心,按(22)式对其他点进行密度修正

(22)

选取密度值最大的点为新聚类中心xck+1。一般取Rb=(1.2～1.5)Ra,定义为一个密度指标函数显著减小的邻域。由(23)式判断xck+1是否满足聚类中心要求

(23)

若(23)式不成立,则xck+1设定为聚类中心,通过(22)式寻找新聚类中心;若成立则聚类结束,输出结果。其中0<δ<1,取值越小则聚类数越多。

4 仿真分析

以经典工业机械臂PUMA560为例,在Matlab环境下进行以下仿真实验:

仿真实验一:采用改进ANGA,适应度函数取(12)式,求得“最柔顺”原则下机械臂逆运动学的最优解。

仿真实验二:采用改进ANGA,适应度函数取(8)式,求得机械臂逆运动学的8个解。

仿真实验三:适应度函数取(12)式,对比改进ANGA与传统ANGA在求解速度及精度上的差异。

PUMA560具有6个转动关节,前三关节确定腕部参考点位置,后三关节决定腕部方位。其D-H坐标系如图1所示。

由图1可得表1所示的PUMA560 D-H参数表。

图1 PUMA560 D-H坐标系

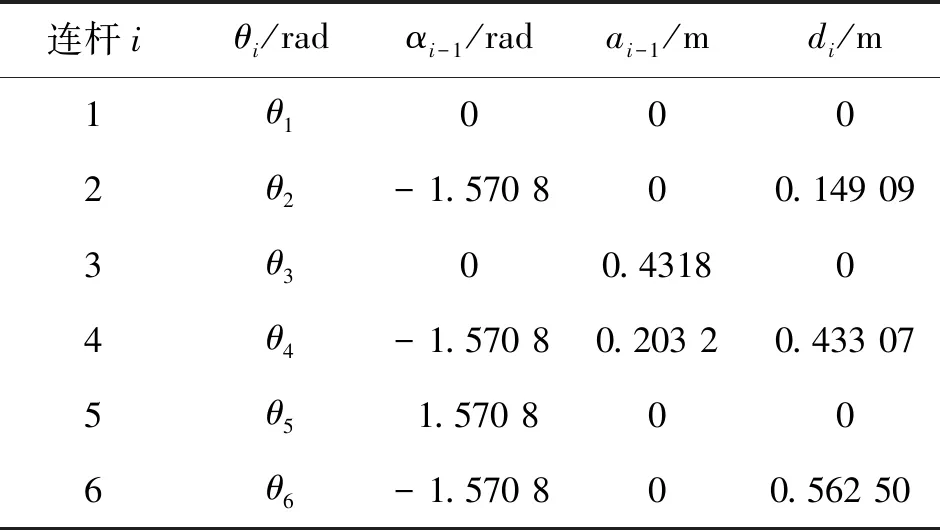
连杆iθi/radαi-1/radai-1/mdi/m 1θ1000 2θ2-1.570 800.149 09 3θ300.43180 4θ4-1.570 80.203 20.433 07 5θ51.570 800 6θ6-1.570 800.562 50

为了体现全部8组解,将其各关节工作范围统一为[-π,π] rad。ANGA算法参数设置如表2所示。

表2 算法参数设置

[1.344 2,0.030 1,0.481 3,1.370 8,1.048 2,-2.965 5]rad。求得了“最柔顺”原则下的最优解。

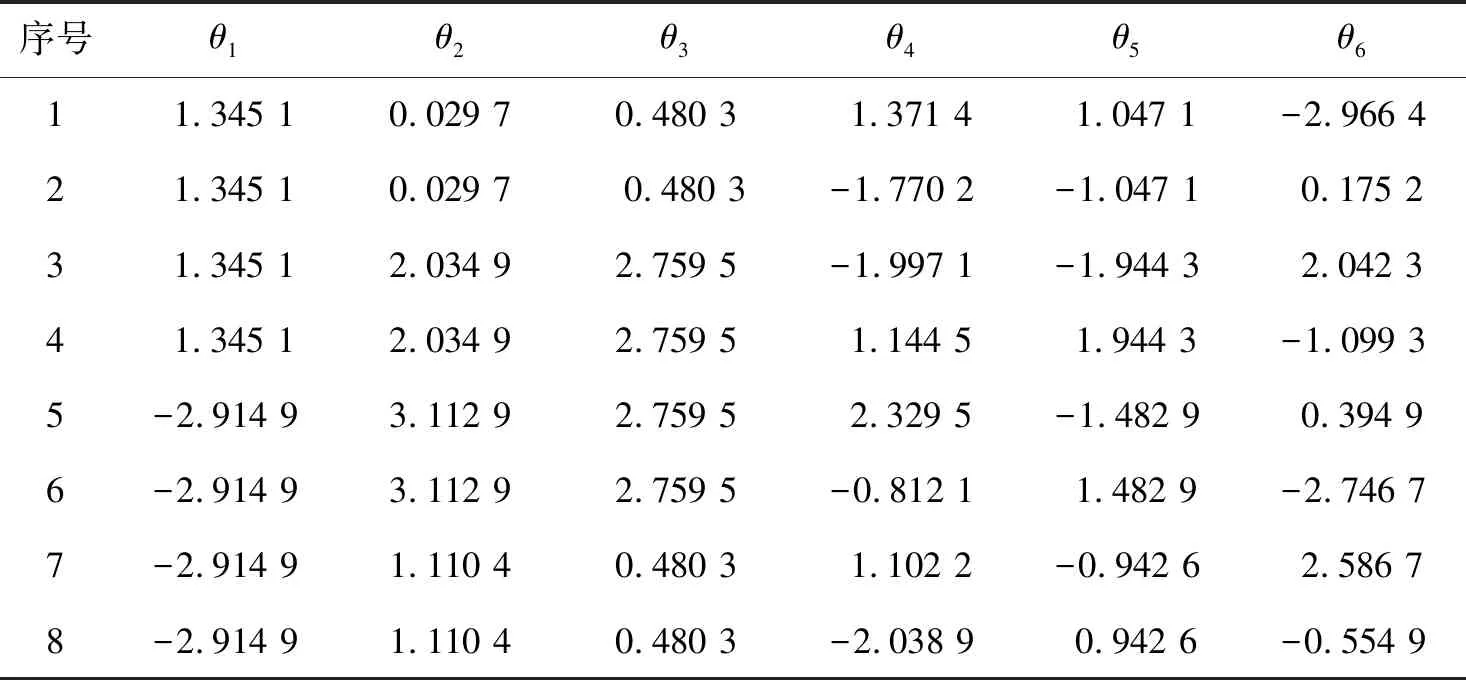
表3 不考虑柔顺的逆运动学求解结果 rad

对应的起始臂形及目标位姿,所得8组逆解臂形及末端抓手朝向分别如图2,3所示。以圆心坐标为(0.2,0.2,0.4) m,半径为0.05 m的球体代表目标物所处位置,以Xe-Ye-Ze坐标系描述目标物的RPY运动姿态。以X-Y-Z坐标系描述末端抓手的RPY运动姿态。

对于求得的8组逆解,由正运动学计算其所对应的抓手位置坐标和RPY角,以检验算法的求解精度。结果如表4所示。

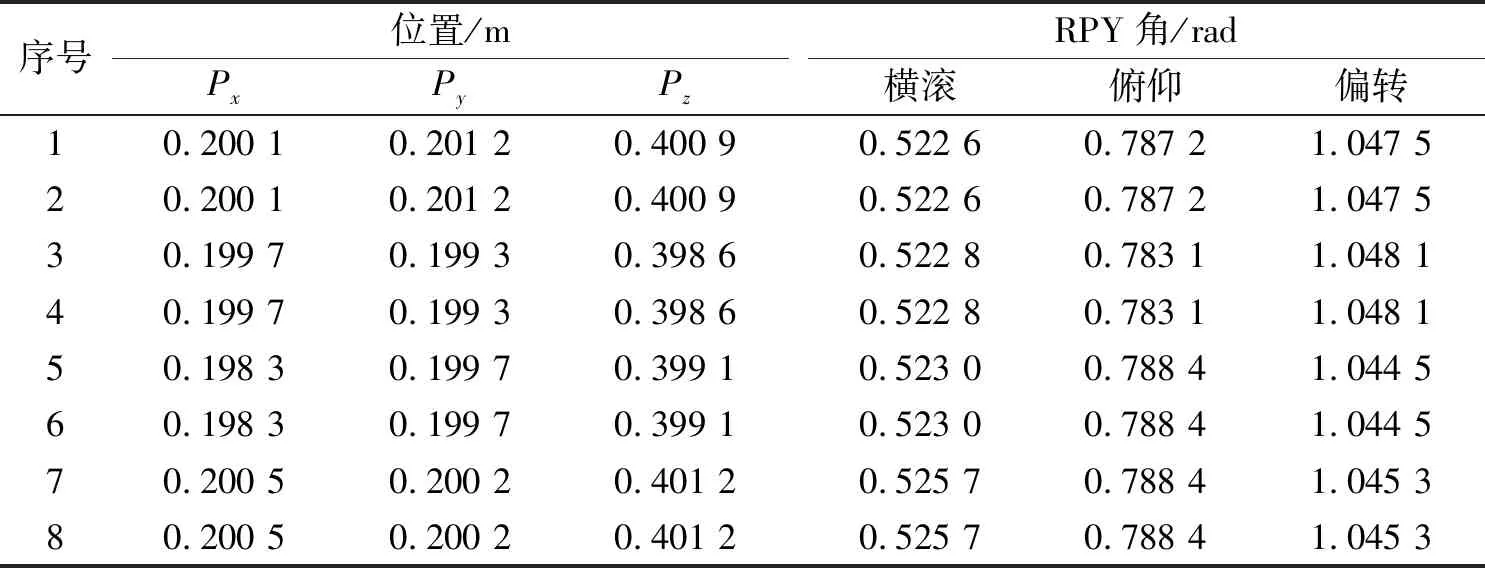
表4 逆解结果对应位置及RPY角

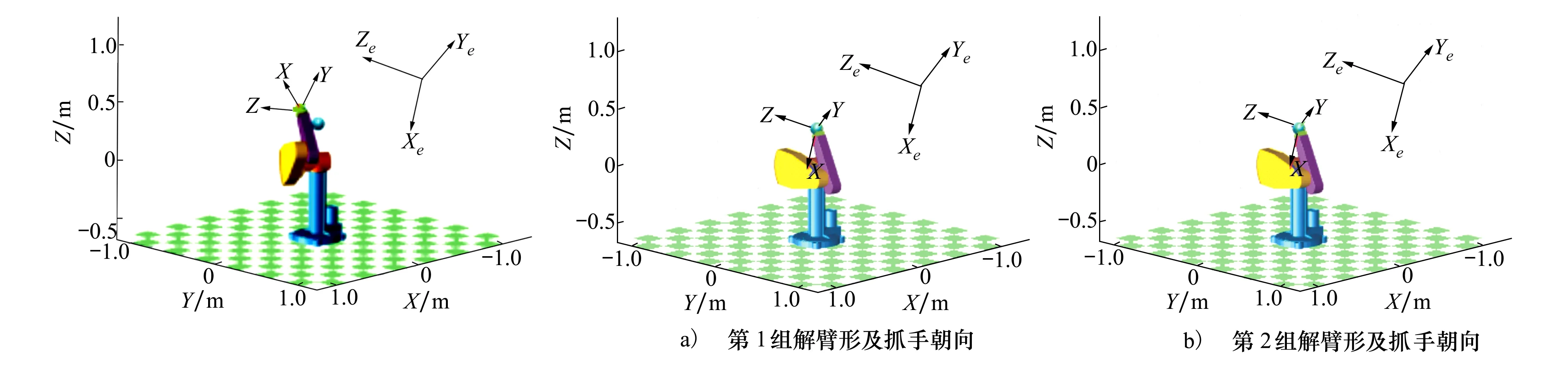
图2 起始臂形及目标位姿图

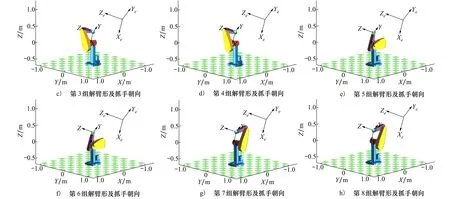
图3 逆解臂形及目标位姿图

图3中a)～h)分别对应表4的第1～8组结果。由表4可知,本文所提出的逆运动学求解算法可求PUMA560固定位姿对应的8组逆解,位置误差在2 mm以内,角度误差在0.2°以内,具有较高的求解精度。

由上述实验结果可以看出,实验一所得最优解与表4所示第1组及图3a)非常接近,而其在8组数据中更满足“最柔顺”原则。因此实验一所得结果即为“最柔顺”原则下的最优解。

仿真实验三中改进ANGA与ANGA的适应度函数均取(12)式,算法参数设定及初始条件同表2,对比适应度值变化曲线,结果如图4所示。并各进行了300次求解,对迭代结束时的最终适应度值进行了对比,如图5所示。

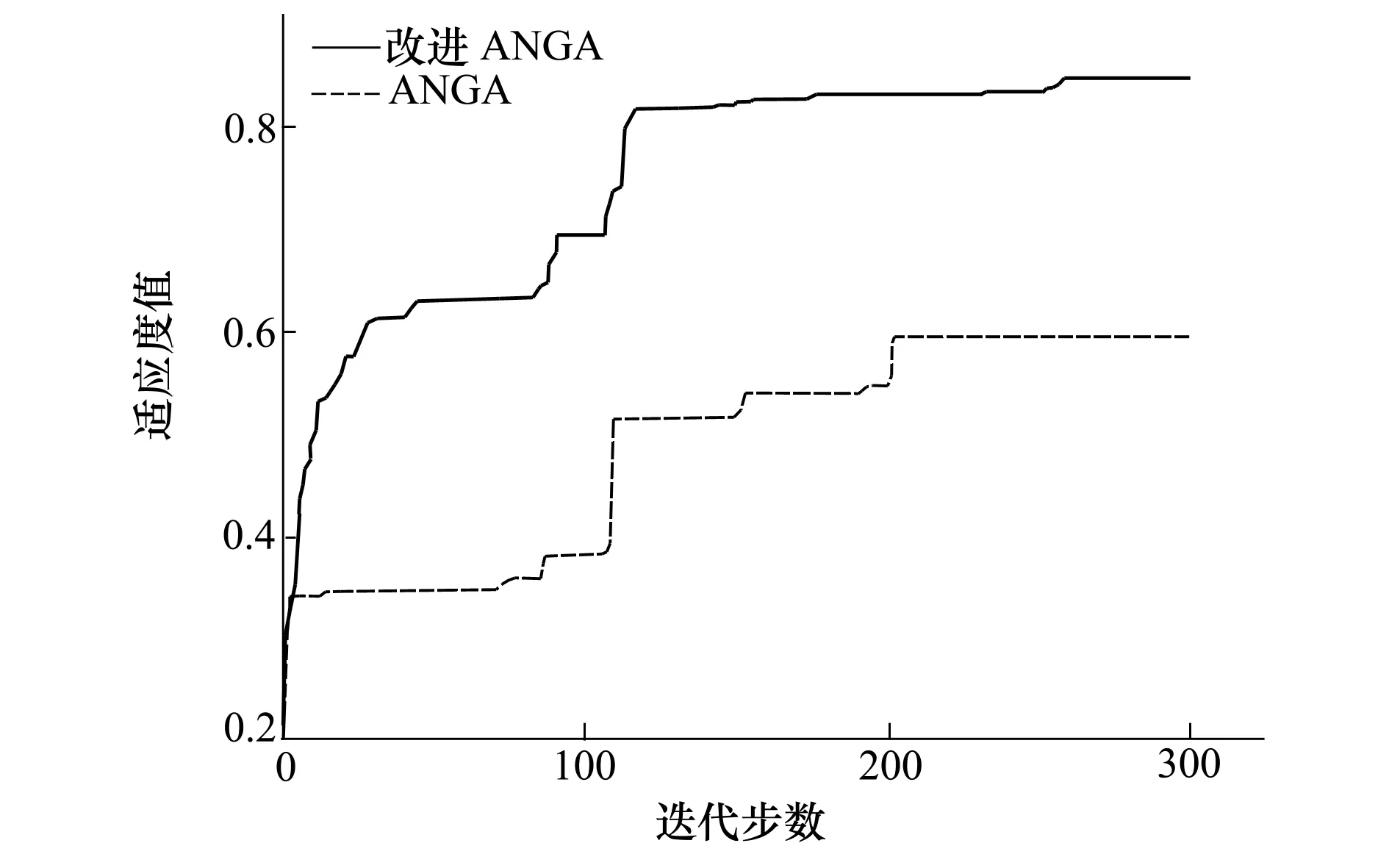
图4 适应度进化曲线对比图

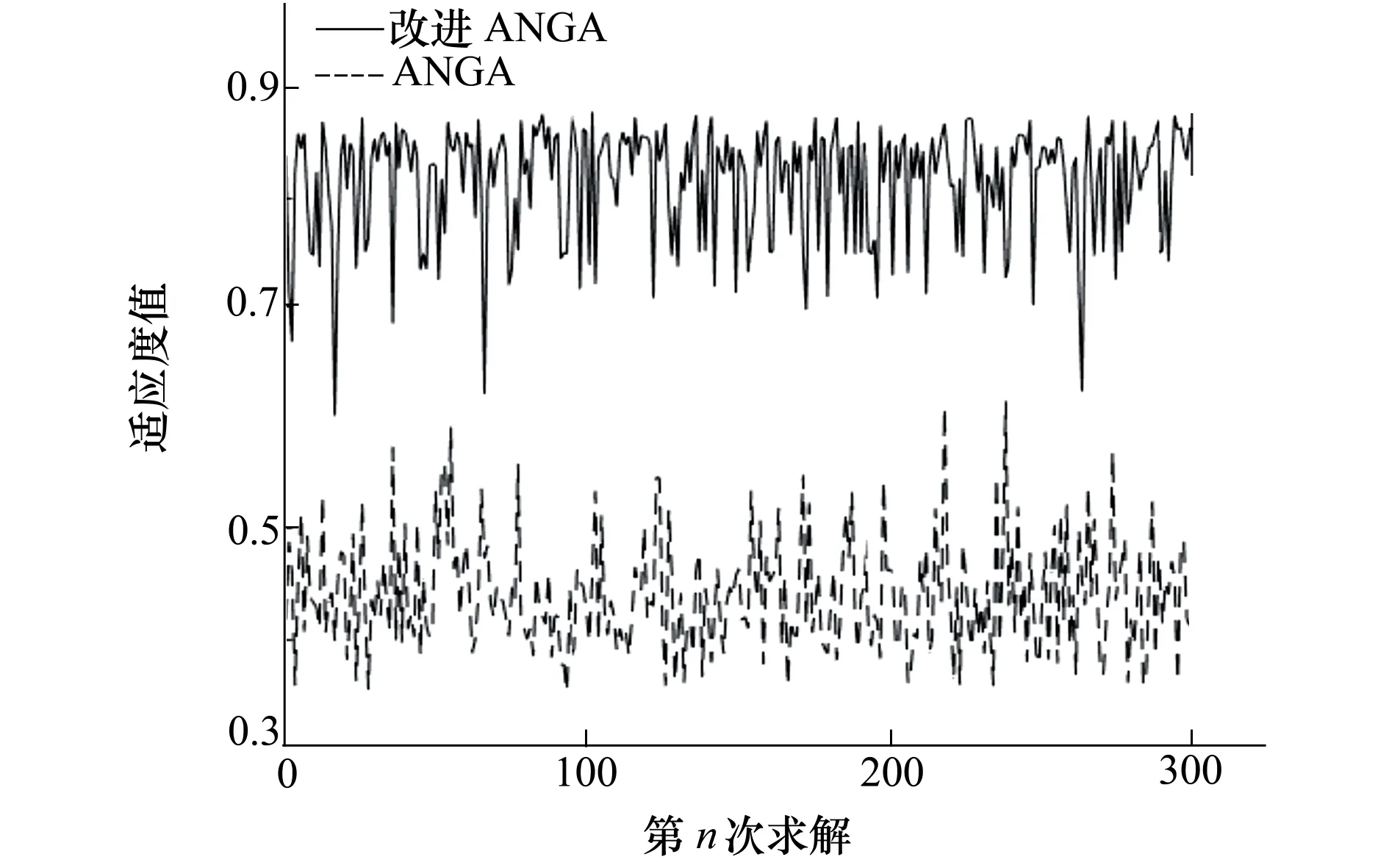
图5 多次求解最终适应度值对比图

由图4可得,采用改进ANGA的适应度值进化速度远高于传统ANGA。图5表明,改进ANGA在300次求解过程中,几乎每次的最终适应度值都大于传统ANGA,由(12)式可知,适应度值越大表明求解结果更为精确。因此,改进ANGA在求解速度及精度上性能更优。

5 结 论

机械臂运动学是笛卡尔空间与关节空间之间的非一对一映射关系,逆运动学求解属于多元多峰函数最优解求取问题。在对逆运动学进行深入分析后,提出了基于改进ANGA的机械臂求逆算法,算法以目标位置及RPY角作为输入,适用于视觉等传感器伺服的机械臂中。融合“最柔顺”原则,求得了最优解,为机械臂的轨迹规划提供了基础。仿真结果表明所提出的改进算法具有较高的求解精度,收敛速度快,无机械臂构型限制。下一步将进行该算法的实验研究,针对实际机械臂系统进行轨迹规划的应用研究。