单排节流孔气浮导轨承载力的数学模型改进与校验分析*

莫德云 马 平2 连海山 弓满锋

(1.岭南师范学院机电工程研究所 广东湛江 524048；2.广东工业大学机电工程学院 广东广州 510000)

由气浮导轨和直线电机驱动技术相结合的工作台，因取消了中间的传动环节，具有摩擦小、定位精度高、无污染等特点，被作为精密定位平台广泛应用于光刻、精密测量和集成电路生产等领域[1-2]。气浮平台的承载力、静刚度等静态特性是判断工作台工作时能否克服倾覆力矩和正常平稳工作的重要指标，因此设计时首先需对结构参数进行校核，以确保能满足工作要求。

气浮平台工程上常用的设计方法可以归纳为数学建模和数值算法两大类。杜建军等[3]通过建立有限元离散化模型分析了节流孔与均压槽对承载能力的影响；陶家生[4]推导了闭式矩形气浮导轨双排节流孔承载力的数学模型；陈爱民[5]使用有限元模型和数学模型对导轨承载能力进行了对比分析等。以上研究使用不同方法对气浮导轨承载力计算进行了数学建模，是当前气浮导轨的工程设计的理论基础。然而当端部节流孔位置不同时导致的端部承载区压力变化，对承载力的影响也是不容忽视的。因此，本文作者在以上学者成果的基础上，根据端部气膜压力分布的特点，对现有数学模型提出了改进的方案，并基于VB语言设计了一款承载性能计算器；建立数值模型对改进模型的假设进行分析；最后，通过实验平台对2种模型的准确性进行校验。

1 气浮导轨工程数学模型的改进

N-S(Navier-Stokes)方程是求解气体润滑问题的主要基本方程式，它由运动方程、连续方程、状态方程组成，给予边界条件后可进行联立方程组求解[6]。在工程上，常对N-S方程进行简化，以便作为气浮导轨结构初步设计的理论依据。工程数学模型中，对N-S方程做了以下假设：(1)气体为理想的层流性质，流动方向平行于导轨平面；(2)气体与导轨间不存在相对滑动；(3)节流器所在平面视为连续高压区，气体只沿宽度方向流出等。此时，压力分布如图1所示。

图1 单排节流孔数学模型解析

设定导轨总长为L，宽度为B=2b，供气压力为ps，节流器出口压力为pd，大气压力为pa，气膜厚度为h。因此，可假设气膜间隙中的流动如图2所示。

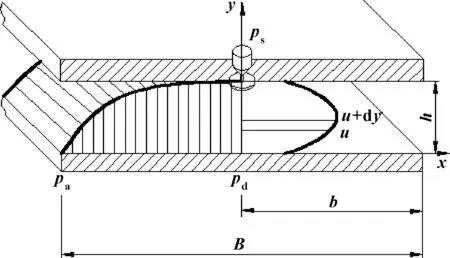
图2 气流模型

依据上述假设，N-S方程可简化为

(1)

式中:η为气体黏度;u为气流在x方向的分量。

积分后可得：

(2)

式中:c1、c2为积分常数。

设置边界条件，当y=0，y=h时，u=0，c2=0，即有：

则式(4)可整理得：

(3)

因此导轨单侧的气体质量为

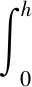
(4)

(5)

式中:R为气体常数，T为绝对温度，这里均看作常数；ρa为大气密度。

因此，积分可得：

(6)

(7)

联立式(6)(7)，可得：

(8)

因此，气膜承载力为

(9)

上述为目前常用的工程数学模型推导过程，然而根据文献[7]的仿真结果和工程经验，高压气体从节流孔排出后向四周端面流动，压力逐渐减小，流速也不断降低，当气体到达边角时已基本从相邻的端面排出，这种情况在气浮导轨的端部更为明显。因此，对单排节流孔承载力数学模型进行改进，改进后的压力分布如图3所示，把导轨区分为端部承载区和主承载区两部分。

图3 单排节流孔改进数学模型解析

对于端部承载区，沿用前面的条件，并假设气体沿半径rz方向均匀流动，没有周向流动，则该区域的N-S方程可简化为

(10)

积分后，代入边界条件，得气膜内不同高度的气体流速：

(11)

因此导轨端部的气体质量为

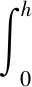
(12)

整理得：

(13)

代入式(11)和气体状态方程，整理可得：

(14)

取p=pd，r=rd和p=pa，r=rz(rz∈min(b,l′)),进行积分、联立方程组，可得：

(15)

所以气膜两端部的承载力之和为

(16)

同时，用主承载区的l代替式(9)中的导轨总长L，则有主承载区的承载力为

(17)

综上所述，分为端部承载区和主承载区后的导轨总承载力为式(16)和(17)的总和：

W=Wz+Wd

为方便后面对数学模型结果进行对比校验，使用VB软件编写了单排节流孔气浮导轨承载性能计算器，如图4所示。

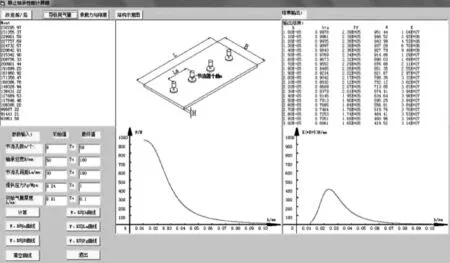
图4 单排节流孔气浮导轨承载性能计算器

2 气浮导轨数值算法的建模与分析

工程中，由于数学模型相对更便捷高效，常用于结构的初步设计。然而对于结构形状或流动状态比较复杂的模型，或者是需要精确分析区域流速和压力分布状态的场合，可以使用有限元数值算法进行分析。

同时，为验证改进数学模型中关于端部流场的假设以及l′对承载力的影响，设定如下三则算例，以建立有限元模型：导轨总长L=250 mm，导轨宽B=50 mm，节流孔个数n=5，供气压力为ps=0.2 MPa，气膜厚度h=0.02 mm，如图5所示。

图5 导轨模型尺寸

调整三则算例的节流孔间距以及节流孔到端面的距离，如表1所示。

表1 算例结构方案

建立气膜有限元模型,选取三维流体单元FlUID142，对气膜模型进行映射网格划分，同时对节流器附近的网格进行局部细化。工作时，气体由节流器顶端流入，经小孔节流后进入导轨，形成高压气膜，再从各气膜端面流出，因此在各节流器顶端施加供气压力ps，气膜各端面施加环境压力pa=0，气膜其余表面和节流器外表面施加速度全约束，设置空气的可压缩性和紊流状态[8-9]，有限元模型网格划分与边界条件如图6所示。

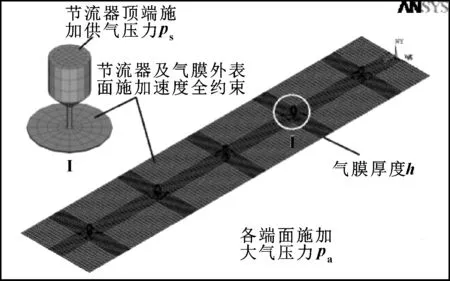
图6 有限元模型网格划分与边界条件

选择标准k-ε湍流模型和BiCGSTAB(稳定双共轭梯度法)进行联合求解。原因是标准k-ε湍流模型是根据湍流理论推导、实验数据得到的一个半经验的模型，在工程领域广泛使用[10]。

湍流动能k及其耗散率ε的运输方程可表达如式(18)(19)所示。

(18)

(19)

式中：μt为湍流黏度，Gk为湍流动能生成项,

(20)

引用Boussinesq假设，可得：

Gk=μtS2

(21)

式中:S为平均应变率,

(22)

根据Launder等的推荐值及后续实验，设置本模型常数[9]为：σk=1.0，σε=1.3，C1ε=1.44，C2ε=1.92，Cμ=0.09。

为帮助气体可压缩性问题的求解，选择BiCGSTAB(稳定双共轭梯度法)求解器，并分4步加载，直到惯性松弛系数为1.0×10-10。

三则算例的有限元模型求解后的气膜压力分布如图7所示。

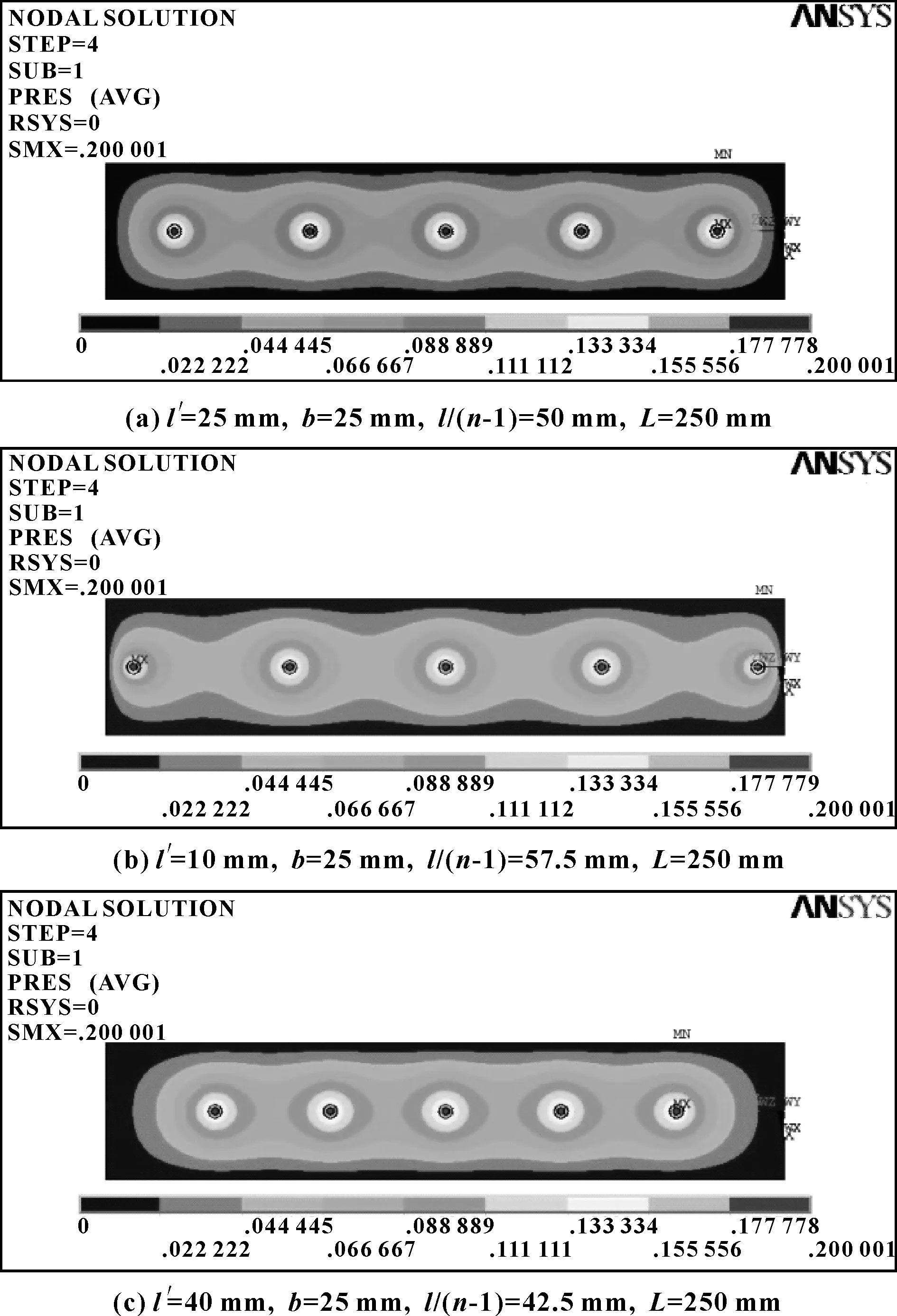
图7 气膜压力分布云图

从仿真结果来看，在节流孔之间形成了较为明显的高压区，节流孔间距越小，高压区越明显；同时，节流孔处的压力最高，向四周端面迅速衰减，在端面降至大气压。

提取上述模型的气膜面节点压力结果进行积分，得出3个方案的承载力分别为673.8、606.2、687.9 N；方案3的承载力最大，比承载力最小的方案2高出13.5%；尽管方案2的压力区面积更大，但方案3更好地利用了导轨的表面形成较为集中的高压区，而方案2中最外侧的2个节流器由于太靠近端面，在外侧并未形成有效的压力区，同时还影响了内侧高压区的形成。

气膜的压力三维分布及等压线如图8所示。

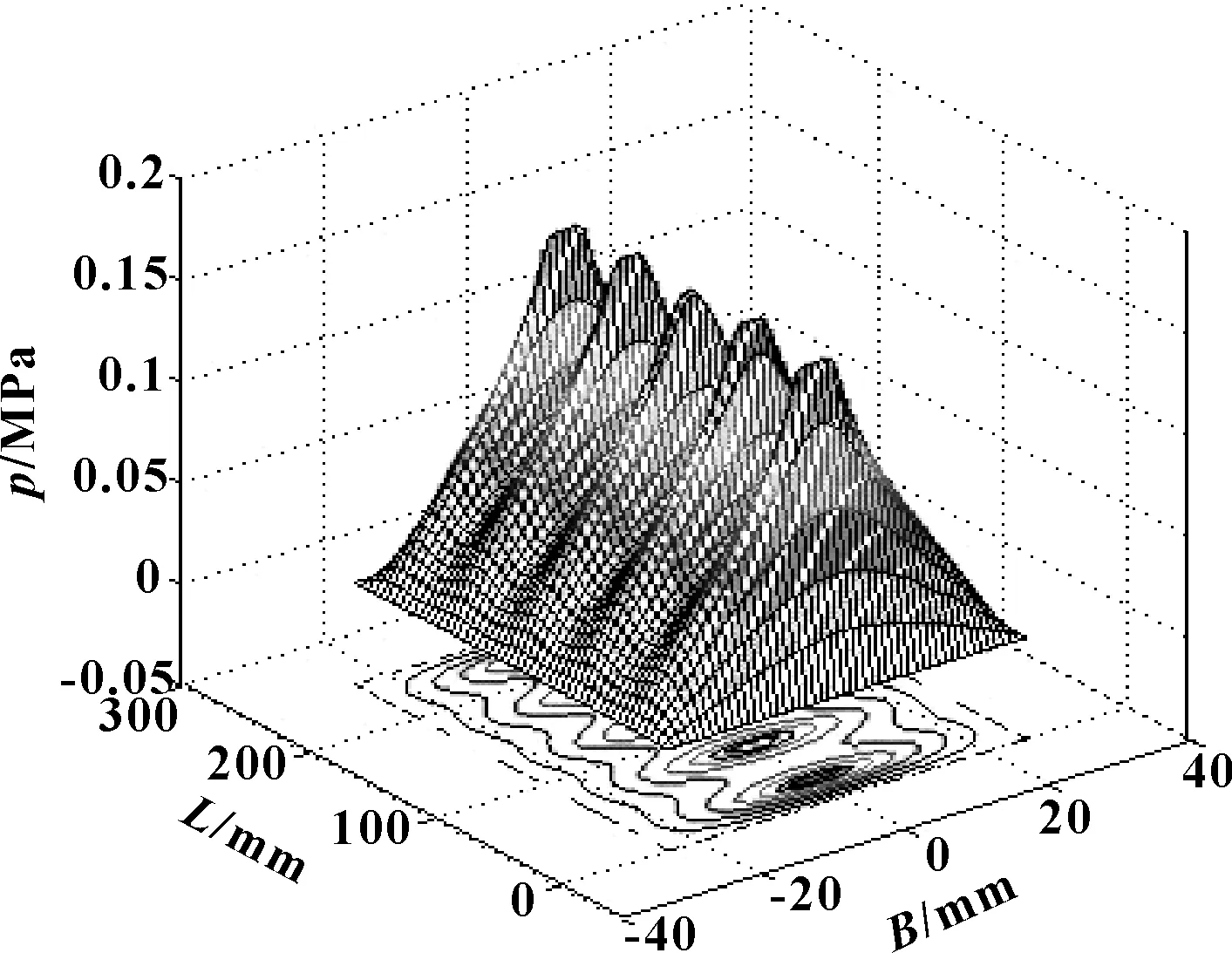
图8 气膜压力分布立体图

综合图7、图8压力分布、等高线分布和承载力结果可以看出，端部节流孔的气流会从与其最近的端面排出，端部承载区压力呈扇形分布，因此当孔与端面间距(l′)发生变化时会引起气膜承载力的变化，而如果按改进前的数学模型，以上3种结构的承载力结果是一样的，从而误导设计。因此在进行工程数学模型的计算，尤其是当b≠l′时，区分端部承载区和主承载区两部分进行分析十分必要，能进一步提高计算精度。

3 气浮导轨承载力测试实验

为校验单排节流孔气浮导轨数学模型改进前后的计算精度，以广东工业大学的直线电机驱动精密气浮定位平台为实验对象，运用DWS电容传感器、示波器数据采集前端、微动台等搭建承载性能实验平台。

DWS型精密电容位移传感器的量程为±20 um，输出电压为±10 V。为避免传感器因温度和使用时间较长出现零点漂移，在实验前进行重新标定，标定如图9所示。

图9 位移传感器标定

以0.02 mm为步进间距调节微动台，通过示波器读取电压变化，每次采集3组数据取平均值，实验两次，通过对数据的拟合得到电容位移传感器灵敏度为103.12 V/mm。

实验用的直线电机驱动精密气浮定位平台采用T形导轨结构，长度800 mm，宽度680 mm，高度300 mm，自身质量197 kg，其中上气膜宽125 mm，下气膜宽95 mm，侧气膜宽150 mm，上下气膜均是b≠l′的结构形式，各气膜面均为8个节流器，搭建的承载性能测试平台如图10所示。

图10 承载能力测试

实验时，先在未供气的状态下采集一次数据，然后保持0.20 MPa的供气压力，让气浮工作台空载5 min，确保工作台完全浮起并处在稳定状态，测量无负载时的数据，并将砝码(10 kg/块)依次加到气浮工作台上，每增加一块读取一次数据，添加6块砝码后为一组数据。测得4组数据经回归处理后如表2所示。

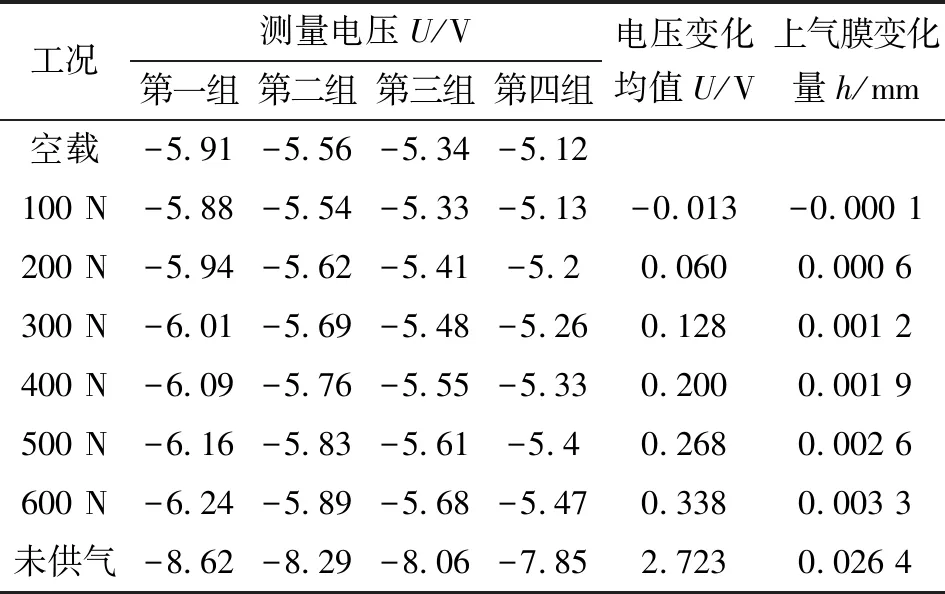
表2 承载力测试实验数据

通过实验发现，气浮实验平台在空载时上气膜厚度为0.026 4 mm，随着负载的增加，上气膜间隙减小，加载到600 N时，上气膜厚度为0.023 1 mm。

对应实验结果，使用上一节的建模方法，取气浮导轨的一侧，建立偏心率为0时，垂直方向平均气膜为0.028 mm的三维有限元气膜模型，其结构如图11所示。

图11 单侧导轨三维模型

分6步施加载荷，得到各气膜面三维压力场分布如图12所示。由仿真结果看出，对于三维模型，各气膜在相交的直角处还会形成相连的高压区。

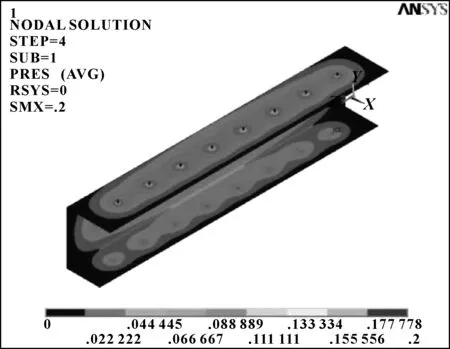
图12 单侧导轨压力场分布

提取不同气膜厚度时的上、下气膜的承载力，得到单边导轨承载力如表3所示。

表3 单边导轨承载力

利用单排节流孔气浮导轨承载性能计算器分别对改进前、后的上、下气膜承载力进行求解，取它们的差为单侧导轨的承载力。经整理，数学模型、数值算法以及实验测试的气浮导轨承载力随气膜厚度变化的结果如图13所示。

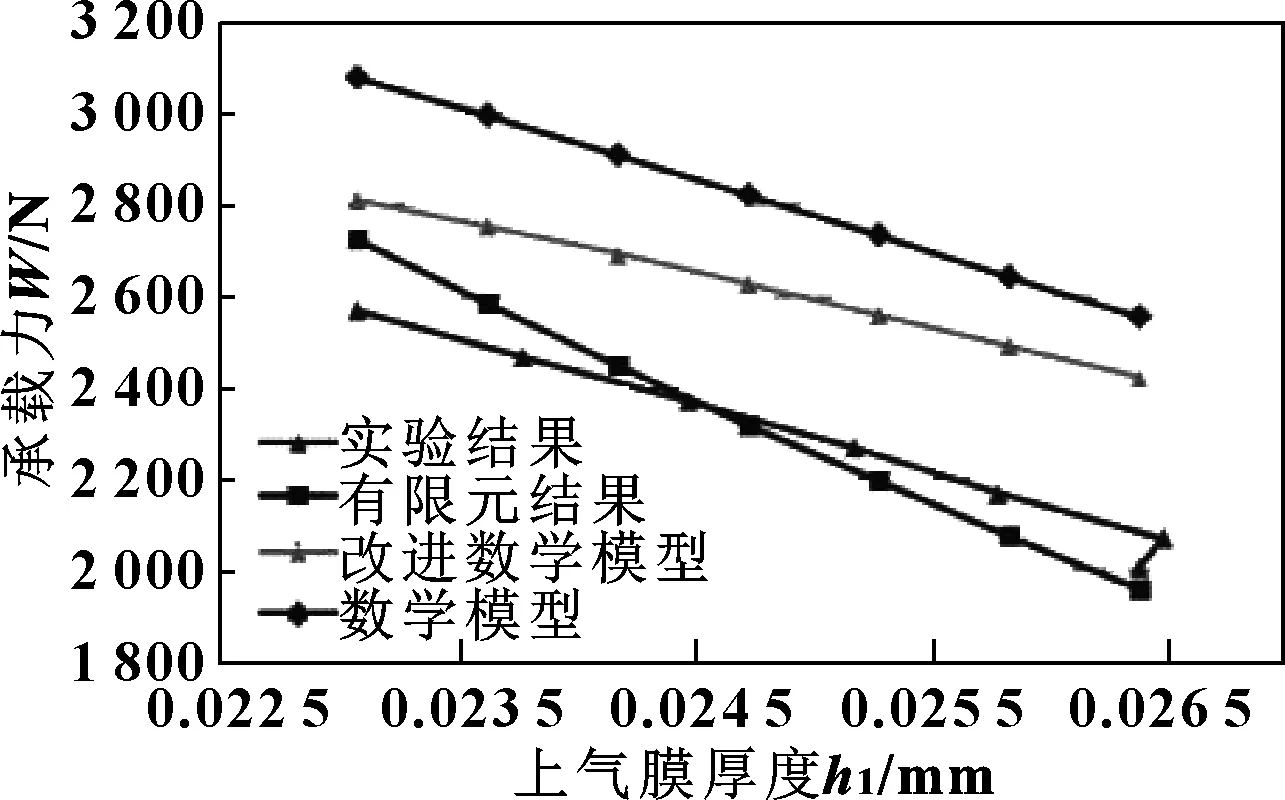
图13 气浮导轨承载力随气膜厚度的变化

如图13所示，在实验测试中，由空载到加载到100 N，上气膜厚度无明显变化；由100 N到600 N时，随着上气膜的减小，承载力呈较好的线性增长。与有限元结果相比发现两者承载力随气膜厚度变化的趋势基本一致，承载力的最大偏差出现在气膜厚度是0.023 1 mm时，约为5.7%，平均偏差为2.9%。出现偏差的主要是原因是有限元模型并未考虑实际工程中的因导轨面平面度、平行度、装配等误差带来的气膜不均等问题。

改进前、后的气浮导轨承载力数学模型求得承载力随气膜厚度变化的趋势与实验结果一致。其中改进后的数学模型结果与实验结果的平均偏差为13.3%，较改进前的平均偏差19.4%提高6.1%。数学模型出现偏差的主要原因是进行主承载区计算时，并未把节流孔之间压力衰减考虑在内，而导致结果大于实际测试结果。

4 结论

(1)对工程上气浮导轨结构设计时常用的数学模型进行改进，并通过实验平台进行验证，结果发现，将气浮导轨分为主承载区和端部承载区后的改进数学模型较改进前的计算精度提高约6.1%，尤其当导轨面宽度、节流孔到端部间距、节流孔间距三者有较大差值时，改进模型能更好地指导气浮平台设计。

(2)对比数值建模分析结果和实验结果发现，该模型能获得较高的仿真精度，工作范围内的平均偏差为2.9%，且能获得较准确的气膜压力和流场工况。