基于CFD的球面动静压气体轴承稳态性能及动态特性分析*
2019-07-022
2
(1.河南科技大学机电工程学院 河南洛阳 471003;2.机械装备河南省协同创新中心 河南洛阳 471003)
动静压润滑即能满足低速下静态支承需要,又在高速下具有保持稳定工作的能力。动压效应受转速影响大,转速越高,偏心大,动压效应也越明显。气体轴承为了获得较大承载,需要增加螺旋槽等结构、增大偏心量、减少平均气膜间隙来增强动压效应,但当转速很高时也会导致气膜涡动的气膜力增大,造成典型的涡动不稳定现象[5-7]。因此,对动静压气体轴承气膜润滑模型的计算与分析,是研究轴承承载性能及动态特性的关键。
对于气体轴承稳定性的分析,大多数学者采用了数值计算和实验测试相结合的方法[8-9],基本上都是先建立雷诺润滑方程,之后对边界条件进行线性化设定,然后使用数值计算方法求解方程组,进而分析轴承的稳态特性。由于雷诺方程不能准确反映轴颈周向动压效应、高速气流周向惯性效应和静压扩散效应之间的非线性耦合关系及其对三维流场特性的影响,因此不能够准确分析动静压耦合效应和轴承的动态特性[10]。
本文作者基于FLUENT建立球面动静压气体轴承气膜的有限元模型,数值计算了气膜网格点上的压力分布,模拟了气膜瞬态流场中复杂的气体流动;分析了运行过程中的气膜间隙、偏心率、供气压力对承载性能的影响规律,以及气膜间隙和偏心率对动态特性的影响规律;研究了气体流场动静压耦合机制,以提高气膜承载性能、优化动态特性、减小气膜涡动,为提高气体轴承运行稳定性提供理论基础。
1 气体轴承的有限元模型
1.1 轴承气膜三维模型
图1所示为球面动静压气体轴承的结构,轴承由转子和定子组成。在轴承的表面开设两排6个节流孔进行供气,在转子上刻有螺旋槽。螺旋槽由台区和槽区构成,一方面将外部压缩气体通过节流孔导入轴承间隙形成静压气膜,产生静压承载;另一方面轴承转子高速旋转时,气体通过楔形间隙流动而产生动压效应,产生动态承载,二者耦合产生轴承动态承载力[11-13]。

图1 球面螺旋槽气体动静压轴承剖面示意图
图1中:β为螺旋角;φ1为轴承直径;φ2为供气孔直径;ω为转速;br为台宽;bg为槽宽;hg为槽区间隙;h0为平均气膜间隙;θ为供气孔角度;α1、α2、α3为包角;θ1、θ2为轴向供气孔角度;θ3是逆切向气体供应孔的切向角。
模型结构参数:φ1=15 mm,φ2=0.2 mm,β=70°,气膜间隙h0=10 μm,α1=26°,α2=32°,α3=85°, 无量纲偏心率ε=0.3,θ1=22°,θ2=38°,θ3=60°。

利用空间球坐标系和螺旋线[14],根据轴承的结构参数应用Pro/E建立气体轴承气膜三维模型。因为气膜厚度一般在几十微米内,在建模时将Pro/E中默认精度改为1 μm。如图2所示。

图2 球面螺旋槽气体动静压轴承气膜三维模型
1.2 控制方程
使用FLUENT模拟气体轴承中的润滑流场,主要求解的方程为质量守恒方程和动量守恒方程。
(1)质量守恒方程

(1)
式中:ρ是气体密度;t是流动时间;div(ρu)是速度矢量u的散度。
(2)动量守恒方程
(2)
式中:μ是动力黏度;u、v、w是速度矢量U在x、y、z三个方向上的速度分量;Su、Sv、Sw是动量守恒方程的广义源项。
1.3 有限元网格模型
利用FLUNT的前处理软件ICEM CFD生成气体轴承气膜的网格模型。由于气体轴承在坐标系中气膜间隙与直径的尺寸大小相差较大,气膜厚度一般在几十微米范围内,在网格生成时为了减小网格负体积出现的概率,使用了分块结构化网格的划分方法。在网格生成后需要检查网格质量,网格密度过高时在供气孔与轴承表面交界处容易出现低质量网格,同时为了提高数值计算精度和控制计算时间,需要反复比较验证不同网格密度的模型,最终整个网格模型的节点数量约为50万。气膜的网格模型如图3所示。

图3 气体轴承网格模型
2 流场数值计算
2.1 FLUENT计算模型与模型假设
2.2.1 流场Realizablek-ε模型
传统气体轴承的求解通常采用层流模型,然而随着气体轴承偏心率、转速及供气压力的增加,对于尺寸较小且结构精度高的气体轴承的数值计算误差较大。球面螺旋槽动静压气体轴承尺寸较小,运转速度最高可达几万甚至几十万转,在轴承高速旋转时,气膜运动会出现涡动和气旋。湍流模型的k-ε模型为双方程模型,包含湍动能k的输运方程和关于湍动耗散率ε的方程。在计算流体力学中使用的k-ε模型,一般有Standardk-ε模型、RNGk-ε模型和Realizablek-ε模型。其中Realizablek-ε模型应用于较高主流剪切率和较大曲率的流动,对旋转流动、强逆压梯度的边界层流动以及复杂的二次流都可以取得较好的计算结果。因此在求解过程中将湍流模型设为Realizablek-ε湍流模型,在供气孔处的气旋现象使用此模型可取得较好的计算结果。
2.1.2 气体轴承气膜的计算模型假设
气体轴承的润滑模型反映了轴承间隙内气膜的压力场和速度场分布、动态承载特性和润滑特性。在求解时中对流体有如下假设:(1)润滑介质为Newton流体,气体黏性系数为常数;(2)气体与壁面间无热量交换,且旋转过程中不考虑轴瓦与轴颈的热变形;(3)在垂直于气膜的厚度方向上,速度变化忽略不计,即压力沿膜厚方向无变化;(4)气体在轴和轴承表面不存在相对滑动;(5)假设壁面光滑,不考虑壁面粗糙及滑移边界的影响。
2.1.3 边界条件的确定
根据模型的计算需要,气体轴承流场计算要设置3种边界条件,分别是压力进口、压力出口和壁面。(1)气体轴承的供气孔和大端为压力进口边界,给定所需的供气压力并设置气体的黏度和密度;(2)气体轴承的小端同样为出口边界,且出口压力设置为环境大气压力,即p0=1.013×105Pa;(3)轴承其余边界设定为壁面,气体与轴承壁面之间无相对滑动,其中气膜内壁面设置为旋转刚性壁面。
2.2 稳态求解计算
将气体轴承网格导入FLUENT后,选择3D压力基隐式求解器;设置流场计算的边界条件。压力速度耦合采用PISO算法,与SIMPLE算法相比较,前者包含两个校正步,在完成第一个校正步后又在第二个校正步再次修正速度和压力方程。由于轴承转子转动时会改变润滑流场,压力离散方式选择PRESTO。在计算过程中监控进出口流量,并且计算时方程的残差收敛标准小于0.000 1时,计算收敛。
稳态计算是在给定的结构参数和运行参数下,假定气体轴承能够在给定的径向偏心和轴向偏心条件下稳定运行,并通过FLUENT模拟气膜间隙中复杂流场流动,数值计算气膜各网格点上的压力场和速度场分布,获得轴承的稳态气膜压力场分布与稳态承载性能。稳态计算流程图如图4所示。

图4 稳态计算流程图
2.3 动态求解计算
气体轴承在给定的结构参数和转速及供气压力条件下运转,通过FLUENT模拟气膜间隙中瞬态流场,数值计算气膜网格点上的压力分布,获得轴承的动态特性。动态计算流程图如图5所示。

图5 动态计算流程图
在动态计算中,选取仿真过程中的一段时间输出每一个时间步长气膜的力、速度和位移,先选取一组数据,然后用其余数据按照下面公式计算动态刚度阻尼系数,观察数据分布并去除失真的数据,最后求取平均值得到轴承的动态刚度阻尼系数。
(3)
式中:ΔFx、ΔFy为两个时间点间轴承气膜压力的变化量;kxx、kyy为主刚度系数;kxy、kyx为交叉刚度系数;bxx、byy为主阻尼系数;bxy、byx为交叉阻尼系数;x、y分别为轴承在x、y方向上位移增量;vx、vy分别为轴承在x、y方向上速度增量。
3 动静压耦合效应与承载性能分析
3.1 轴承气膜压力分布与动静压耦合效应
球面动静压气体轴承的气膜压力分布主要受到结构参数和转速及供气压力的影响。通过轴承气膜压力分布特性分析,研究了静压与动压相互耦合对轴承稳态承载性能的影响。
轴承的结构参数为:径向无量纲偏心率ε=0.3,螺旋角β=70°,槽深比为3.6,槽宽比为0.4,槽数为6,切向角θ3=55°。
3.1.1 供气压力0.6 MPa时的气膜压力分布
轴承的运行参数设为供气压力0.6 MPa,转速30 000 r/min。图6(a)所示为气膜厚度为10 μm的压力云图,图6(b)所示为平均气膜间隙h0分别取5、10、20 μm时供气孔处的周向压力分布图。从图6可以看出:气膜压力主要是由于外界供气产生的,在供气孔附近区域气膜压力明显增强;气体流动时具有一定的楔形效应,产生的动压效应较弱;槽台交界处产生动压增强效果不明显,气膜厚度减小有助于动压效应的产生。可见,供气压力大时,气膜的承载能力与动态特性主要取决于静压效应。

图6 气膜压力云图和周向压力分布图(p=0.6 MPa)
3.1.2 供气压力0.1 MPa时的气膜压力分布
研究了供气压力较小时静压与动压相互耦合对轴承稳态承载性能的影响。轴承的运行参数设为供气压力0.1 MPa,取平均气膜厚度h0=10 μm。图7(a)所示为30 000 r/min转速时的压力云图,图7(b)所示为转速分别为10 000、30 000、60 000 r/min时供气孔处的周向压力分布图。由图7可以看出:供气压力很小时,气膜的承载性能主要由动压效应产生;气体流动具有楔形效应,气膜压力分布明显出现收敛区和发散区,其中发散区的气膜压力迅速减少,部分区域出现负压;收敛区的气膜压力逐渐增大,气膜压力最大发生在接近气膜间隙最小的区域;在轴承螺旋槽的槽台交界处,气膜压力有明显的突变现象,在交界处的一侧气膜压力骤降,另一侧的气膜压力骤增;转速越高,动压效应越明显,螺旋槽有效增强了动压效应。

图7 气膜压力云图和周向压力分布图(p=0.1 MPa)
3.1.3 供气压力0.3 MPa时的气膜压力分布
轴承的运行参数设为供气压力0.3 MPa,取平均气膜厚度h0=10 μm。图8(a)所示为30 000 r/min转速时的压力云图,图8(b)所示为转速分别为10 000、30 000、60 000 r/min时供气孔处的周向压力分布图。由图8可以看出:在轴承供气孔附近静压效应明显增强,同时螺旋槽处出现动压增强效应,并且气膜压力随着转速的增加而增大,共同形成动静压耦合效应,承担气膜承载性能,并使得在周向方向压力分布更趋均匀,承载分布更合理;动压效应受转速影响大,转速越高,偏心大,动压效应也越明显。因此,动静压轴承可以在保持合理的动压效应的同时,通过增加供气压力来增强静压效应,进而提高轴承承载性能;另外在大幅提高承载性能的同时,也更有利于在大承载下更好地保证稳定性。当转速很高时,随着供气压力的增大,轴承静压产生的承载性能增加幅度变弱,但此时由于高转速下动压效应增强幅度较大,使得动静压耦合承载能力更强。因此,动静压耦合可以更好地相互补充,既可以增加气膜的承载性能,又能优化动态特性,提高高速运行的稳定性。

图8 气膜压力云图和周向压力分布图(p=0.3 MPa)
3.2 运行参数对稳态承载力的影响分析
3.2.1 气膜厚度对承载力的影响
图9所示为轴承承载力随转速及气膜厚度的变化曲线。不同转速下,轴承承载力随气膜厚度的变化趋势总体上相同,即随着气膜厚度的增加,轴承承载力迅速减小,在气膜厚度大于10 μm以后减小的趋势变缓。气膜厚度越大,产生的动压效应越小,承载力变化逐渐趋于稳定,承载性能主要取决于供气压力产生的静压效应,因而为保证较高的承载性能,气膜厚度选择不大于10 μm。另外,随着转速增加承载力逐渐增加,轴承的动压效应逐渐变强,使得动静压耦合效应增强,既可以提高轴承气膜承载性能,又能提高其抗干扰能力。

图9 气膜厚度对承载力的影响
3.2.2 偏心率对承载力的影响
图10所示为轴承承载力随转速及偏心率的变化曲线。不同转速下,轴承承载力随偏心率的变化趋势总体上相同,即轴承承载力随着偏心率的增大呈不断增大的趋势。当偏心率小于0.3时,承载力呈线性增加但趋势较缓,转速对承载力的影响也较弱;偏心率超过0.3后承载力迅速增加,转速越高,承载力增加幅度越大。偏心率越大,产生的动压效应也越明显,轴承的承载性能与抗干扰能力越好,但偏心率增大,最小气膜厚度减小,轴心涡动增大,不仅给轴承设计和加工精度增加了困难,而且在轴承运行过程中容易发生碰磨导致失效。因此,合理地选择偏心率,即可以增强动压效应,提高轴承承载性能,也有利于改善轴承的稳定性。
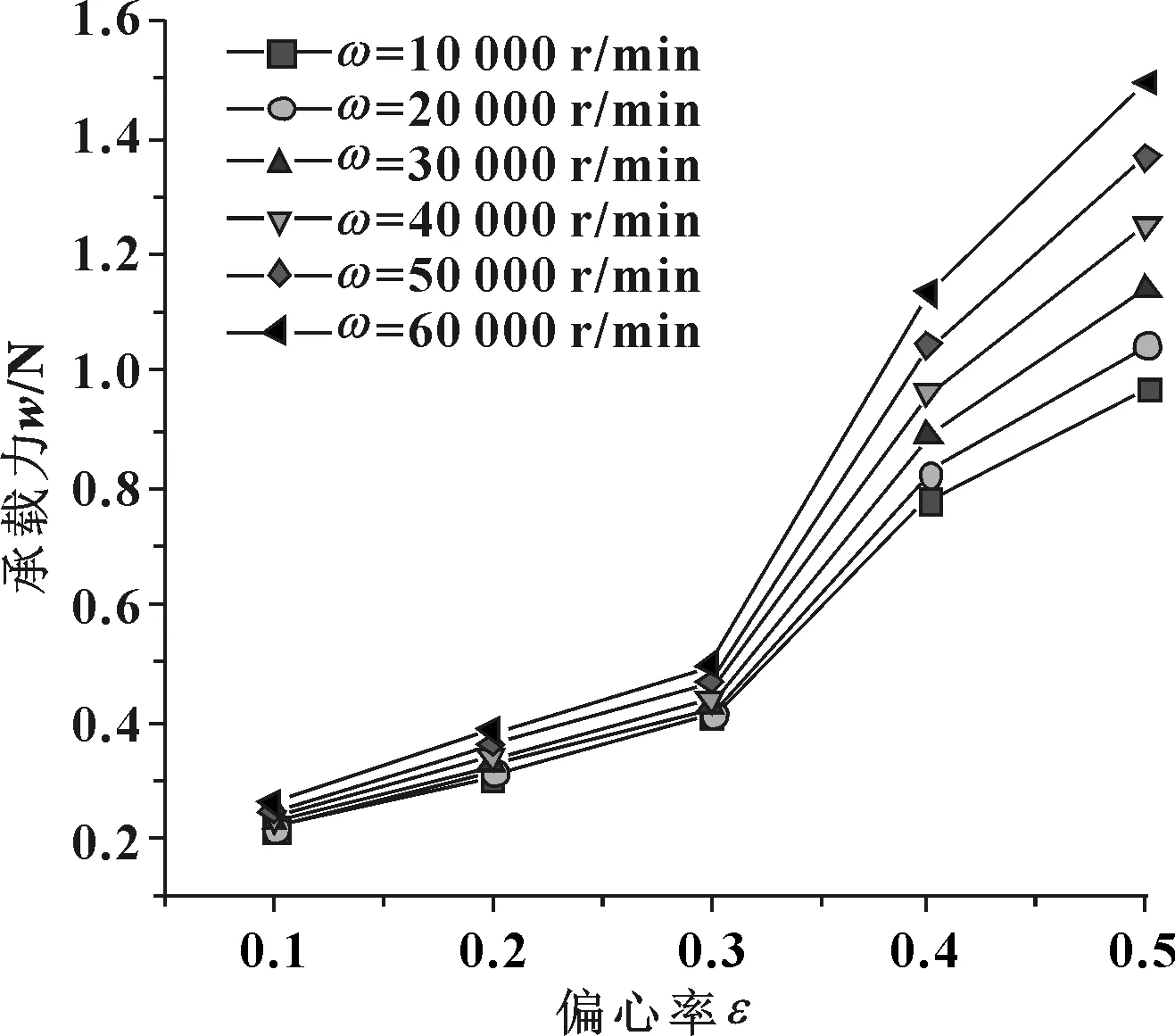
图10 偏心率对承载力的影响
3.2.3 供气压力对承载力的影响
图11所示为轴承承载力随转速及供气压力的变化曲线。不同转速下,轴承承载力随供气压力的变化趋势总体上相同,即随着供气压力的增大,轴承的承载力呈不断增大的趋势。在供气压力小于0.3 MPa时,轴承承载力随供气压力增大的趋势较缓,此时转速增加产生的动压效应越明显,动静压耦合产生的承载性能越好;供气压力大于0.3 MPa后,承载力迅速呈线性增加,随供气压力增大而产生的静压效应占主导作用,转速增加产生的动压效应对承载力的影响变弱。
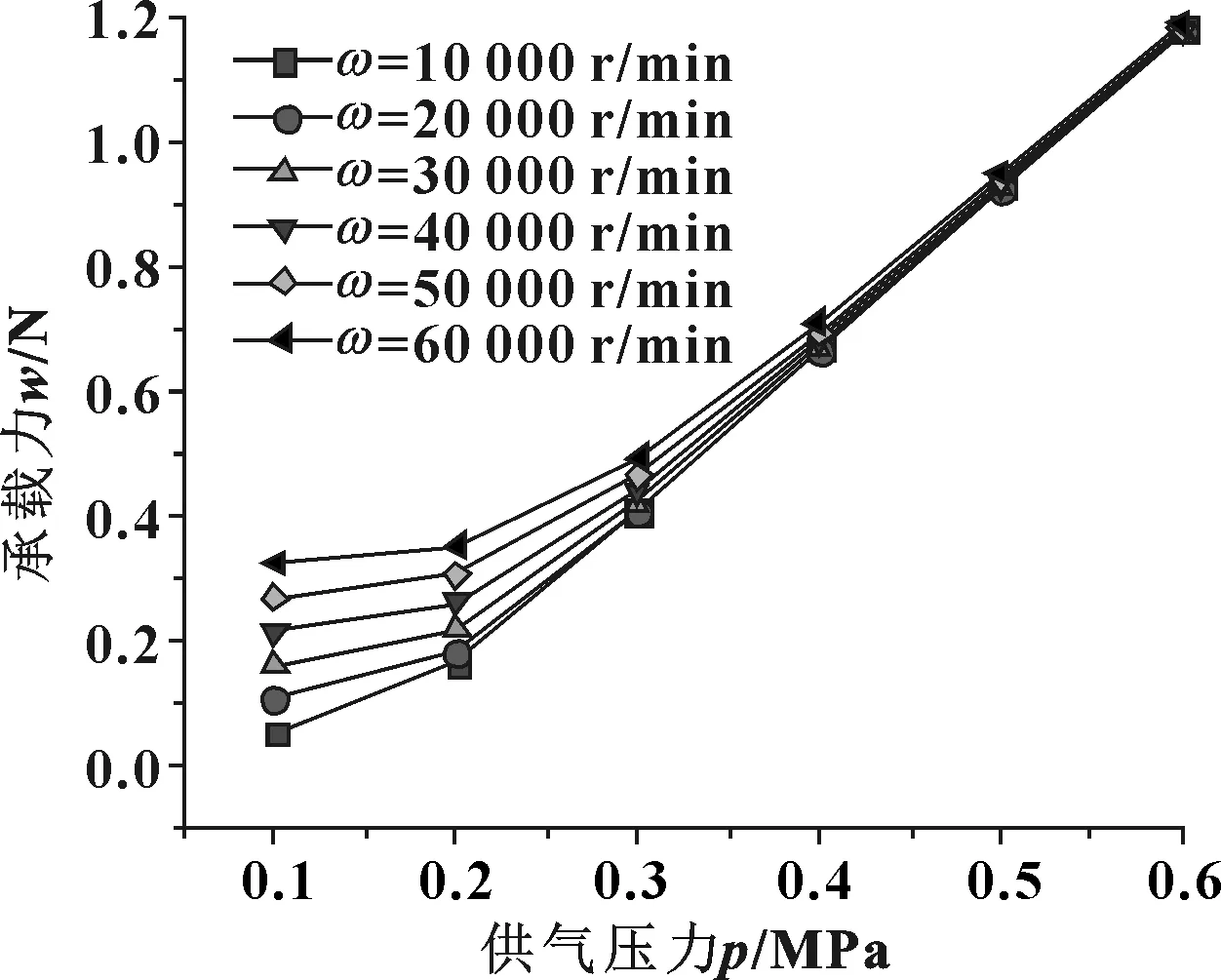
图11 供气压力对承载力的影响规律
4 动态特性分析
动静压气体轴承在高速运行时,转速、供气压力、偏心率等的变化,会引起气膜内部流场变化,会重构气膜的动态特性,引起气膜厚度和压力分布、非线性气膜力、承载性能、动态特性和稳定性的变化[15-17]。
设置轴承的运行参数为:供气压力0.3 MPa,转速40 000 r/min,结构参数为:径向无量纲偏心率ε=0.3,螺旋角β=70°,槽深比3.6,槽宽比0.4,槽数6,切向角θ3=55°,研究气膜厚度、偏心率对动态特性系数的影响。
4.1 气膜厚度对动态特性系数的影响
从图12(a)可以看出:轴承的刚度系数随着气膜厚度的增大呈先增大后减小的趋势,其中主刚度系数Kxx、Kyy变化趋势较为明显,交叉刚度系数Kxy、Kyx变化趋势较缓;当气膜厚度为10 μm时轴承的主刚度系数最大。从图12(b)可以看出:随着气膜厚度的增大,轴承的主阻尼系数方向相反并且呈先增大后减小的趋势,其中主阻尼系数Bxx、Byy变化趋势较为明显,交叉阻尼系数Bxy、Byx变化趋势较缓。
随着气膜厚度的增大,动压效应逐渐减弱,气膜承载性能减小,总体上轴承的刚度系数随着气膜厚度的增大呈减小的趋势;轴承刚度系数的增大的原因是受小孔节流供气方式的影响,由于节流器效应和供气孔分散损失减少,小孔节流供气方式在最佳轴承间隙处增加了轴承刚度。气膜的阻尼对涡动能量是起消耗作用,阻尼越大抑制涡动作用就越强;随着气膜厚度的增大,轴承的稳定性变差,气膜的阻尼减小。为了使轴承气膜有较大的刚度和阻尼,同时又有较高的承载性能,气膜厚度选取在8~12 μm之间。

图12 气膜厚度对刚度系数和阻尼系数的影响
4.2 偏心率对动态特性系数的影响分析
从图13可以看出:主刚度系数Kxx、Kyy随偏心率的增大呈不断增加趋势,在承载方向上的刚度系数Kyy比非承载方向上的刚度系数Kxx大,交叉刚度系数Kxy、Kyx受偏心率的影响较弱,变化趋势较小;阻尼系数Byy、Bxy受偏心率的影响较弱,变化趋势较小,主阻尼系数Bxx随着偏心率的增加而增加,偏心率大于0.3后增加趋势明显,交叉阻尼系数Byx随着偏心率的增加而减小,偏心率在0.2~0.3之间减小趋势明显。

图13 偏心率对刚度系数和阻尼系数的影响
气膜的阻尼对涡动能量起消耗作用,是抑制涡动的一种因素,阻尼系数表征的是力随速度的变化率。随着偏心率的不断增大,气膜动压效应增强,因而转子克服气膜力做的功越多;轴承的主阻尼系数随着偏心率呈不断增大趋势,抑制涡动作用就越强,轴承转子系统运行就更加稳定。为了使轴承气膜有较大的刚度和阻尼,同时又有较高的承载性能,偏心率选取在0.4~0.5之间较为合理。
5 结论
(1)基于FLUENT数值计算方法可以反映轴承气膜润滑流场的动态压力变化,能够研究动静压耦合对轴承润滑流场压力分布的影响。动静压气体轴承的承载能力主要由供气压力产生的静压效应和轴颈旋转产生的动压效应组成,供气压力的增加可以有效地增强静压效应,气膜厚度减小和转速增加有助于增强动压效应,使得动静压耦合产生的承载能力更强。
(2)不同的转速、供气压力、气膜厚度和偏心率,引起气膜润滑流场的压力变化,对轴承运行过程中承载力有较大的影响。分析表明:较高的转速和供气压力使轴承的动静压耦合效应逐渐变强,明显地提高轴承的承载力;适当地减小气膜厚度和增大偏心率也可以大幅提高轴承承载性能。因此,动静压耦合可以更好地相互补充,既可以提高轴承承载性能,也有利于改善轴承的稳定性。
(3)对于动静压气体轴承,轴承刚度系数随着气膜厚度的增大呈先增加后减小的趋势,随着偏心率的增加而增加;轴承阻尼系数随着气膜厚度和偏心率的增加变化较为复杂,整体上呈增大的趋势。气膜的交叉刚度系数起到促进涡动的作用,气膜的阻尼系数是一种抑制涡动的因素,气膜的稳定性取决于气膜的刚度与阻尼的相互作用。因此,合理地选取气膜厚度和偏心率参数可以增加气膜承载性能,优化动态特性,减小气膜涡动。
