轴瓦变形计算模型对不对中滑动轴承润滑特性的影响*
2019-07-02何振鹏1谢海超2王伟韬邓殿凯
何振鹏1,2 谢海超2 王伟韬 邓殿凯 张 淳
(1.中国民航大学天津市民用航空器适航与维修重点实验室 天津 300300;2.中国民航大学航空工程学院 天津 300300;3.中国民航大学中欧航空工程师学院 天津 300300)
目前,国内外学者在计及轴颈倾斜和轴瓦弹性变形的滑动轴承润滑的耦合分析方面做了许多工作。孙军等人[1]研究了轴受载荷变形产生的轴颈倾斜对滑动轴承性能的影响,分析了倾斜轴颈轴承的最大油膜压力、泄漏流量、轴承承载力和轴承力矩等性能随倾斜程度的变化。谢帆等人[2]采用有限差分法对径向滑动轴承油膜压力分布进行了计算,对传统求解方法进行了改进,同时考虑了偏心率和偏位角两者的变化。何芝仙等[3-4]采用变形矩阵方法,计算单位油膜压力作用下轴承表面的径向变形量,但未考虑轴颈倾斜和弹性变形耦合因素的影响。总体来说,由于摩擦学理论本身比较复杂,对于轴颈倾斜、弹性变形、轴瓦表面粗糙度以及轴颈旋转产生的热效应等多种因素耦合分析还需要进一步深入研究[5]。
本文作者在深入研究滑动轴承摩擦副系统润滑机制的基础上,研究了轴受到载荷作用产生变形导致的轴颈在轴承孔中倾斜及轴瓦弹性变形,对径向滑动轴承流体动压润滑性能的影响。研究时,根据发动机主轴承不同安装特点,将主轴承中轴承结构分为半悬空和全部固定2种结构形式;考虑到轴承轴瓦实际安装情况,将轴瓦与主轴承座的连接形式简化为接触和固定2种模型,采用有限差分方法结合松弛迭代求解润滑控制方程,分析在轴颈倾斜和弹性变形耦合作用下最大油膜压力、端泄流量、承载力和轴承力矩随偏心率、转速之间的变化关系,并与传统模型进行对比研究。
1 基本方程和公式
1.1 不对中轴颈流体动力润滑模型
在实际润滑分析中主要是针对阶梯轴进行,任何复杂的轴系均可模化成阶梯轴形式,图1所示为多个阶梯跨度下轴颈受载倾斜模型。
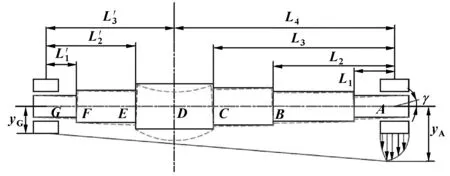
图1 复杂转子的不对中角度模型
在以往不对中径向滑动轴承润滑分析中,未考虑复杂结构特点和非对称引起的不对中角度转子结构的影响。为此,本文作者在前期研究复杂阶梯轴端不对中角度计算方法、非对称结构引起的不对中角度对润滑特性影响的基础上,从轴瓦变形计入润滑模型角度分析了轴瓦变形对润滑精度的影响。
1.2 轴颈在轴承中倾斜时油膜厚度表达式
图2为轴颈倾斜状态下示意图,油膜厚度可表示[6]为
(1)
式中:c是半径间隙;e是轴承中心截面偏心距;θ是从z轴正方向起的角坐标;φ是轴承与轴颈中心的连线OC2与z轴的夹角;γ是轴颈在轴承中的倾斜角;l是轴承宽度;α是OC2与C1C3之间的夹角;其中C1、C2、C3是轴颈轴向与前端面、中间截面、后断面的交点。

图2 轴承轴颈倾斜示意图
1.3 轴承机油端泄流量
轴承前端面和后端面流出润滑油的流量分别为
(2)
(3)
轴承总端泄流量为
Q=|Q1|+|Q2|
(4)
1.4 轴承油膜力矩
倾斜轴承轴颈中央截面两侧的油膜压力不对称,油膜压力会对轴颈产生一定的力矩M。油膜力矩在x方向和y方向的力矩分量为
(5)
(6)
总油膜力矩为
(7)
1.5 轴承油膜承载力
如图2所示,油膜承载力在x方向和y方向的分量为
(8)
(9)
油膜总承载力为
(10)
1.6 雷诺方程的离散过程
Reynolds方程是流体动压润滑的基本方程,求解润滑控制方程是润滑计算的基本内容。对工况做如下假设[7]:(1)流体为牛顿流体,符合牛顿黏度定律;(2)流体为层流,没有湍流的影响;(3)忽略流体惯性力、流体离心力及重力影响;(4)油膜压力沿膜厚方向不变;(5)与沿膜厚方向的速度梯度相比,其他速度梯度太小而忽略。简化后的轴承润滑控制方程为
(11)
式中:h是油膜厚度;ρ是润滑油密度;p是油膜压力;U是沿x方向的速度;σ为两表面的粗糙度;φx、φy是压力流量因子,表示粗糙表面间的平均压力流量与光滑表面间的压力流量之比;φs为剪切流量因子,反映两粗糙表面相对滑动时产生的附加流量的影响。
考虑轴颈倾斜的影响,油膜压力沿轴承轴向不对称于中央截面,如图3所示,在求解区域内在轴向取轴承全宽,在周向方向取360°,在整个求解区域内划分网格,在轴向取100节点,在周向取110个节点,将轴瓦的油膜划分成110×100的网格,用各个节点上的压力值构成各阶差商,近似地取代Reynolds方程中的各阶导数。

图3 油膜网格划分
应用中心差分方法,将Reynold方程进行离散,构造出的差分格式[8-9]为
(12)
(13)

构造差分方程为
(14)
将上述构造的差分表达式(13)代入到式(14)中得到:
(15)
(16)
(17)
(18)
(19)
(20)
根据上述的差分方程表达式,可以用 (i,j)节点周围四节点的压力值来计算该节点的压力值,边界条件采用Reynold边界条件,这种边界条件与实际情况接近。
2 不同轴瓦模型的弹性变形研究
为了尽可能反应轴瓦变形的实际情况,模拟轴瓦在不同条件下的变形,文中采用了3种不同的模型来模拟轴瓦的变形情况,图4所示为3种不同的轴瓦模型。图4(a)中只是单纯的轴瓦,图4(b)中轴瓦与外部形成一体,图4(c)中轴瓦与外部接触。文中研究时忽略了轴承安装过程中的安装变形,后续研究将针对安装变形后热机耦合作用下轴承的变形对轴承润滑性能的影响。
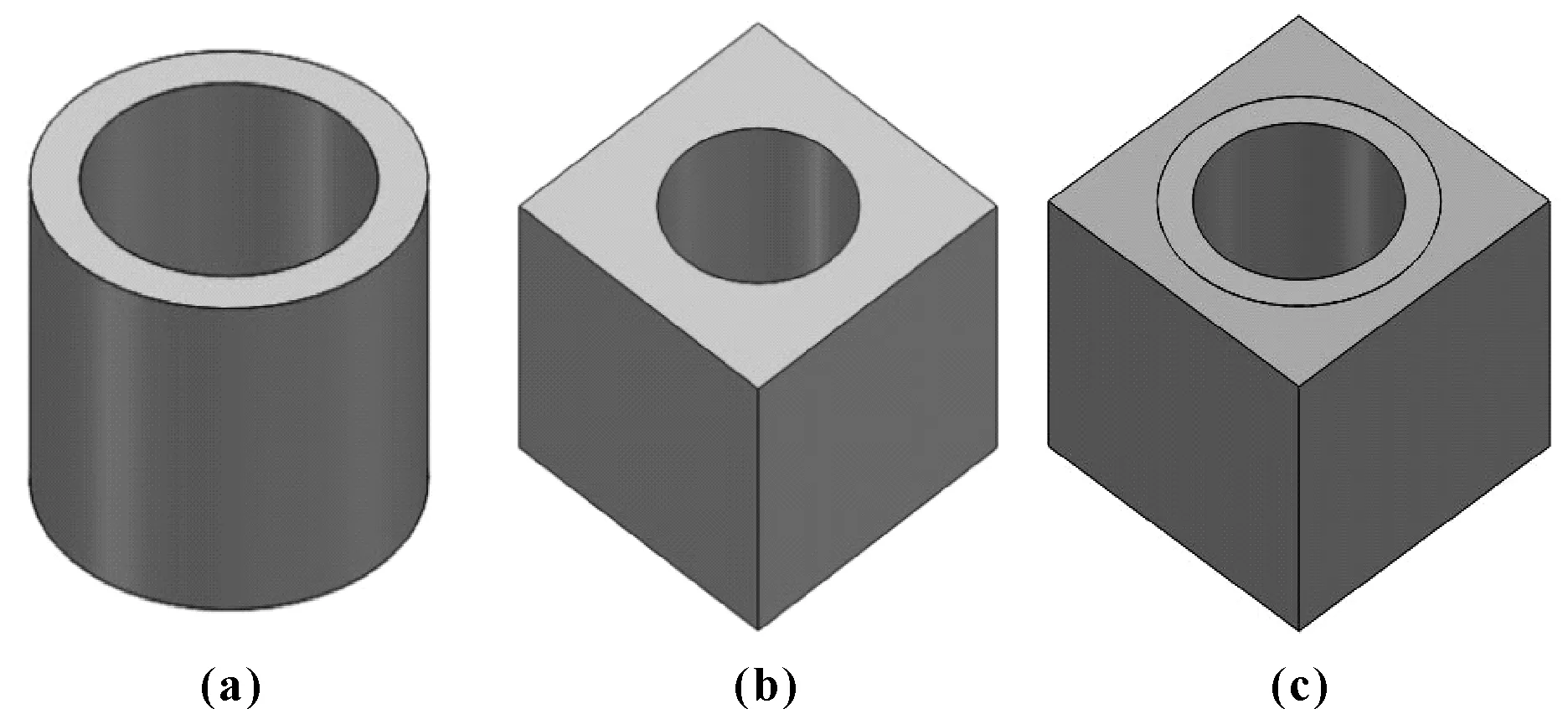
图4 不同的轴瓦结构模型
采用如图5所示的5种模型研究轴瓦的弹性变形情况,图5(a)中轴瓦的外侧全部约束(以下简称为模型5(a) ),图5(b)、(c)中则是轴瓦的外侧全部约束和约束一半,内部轴瓦和轴承座为一体(以下简称为模型5(b)和5(c)),图5(d)、(e)为轴瓦与轴承接触模型(以下简称为模型5(d)和5(e))。为计算轴瓦表面变形,在图5所示的轴瓦内侧施加单位压力,计算5种约束条件下的弹性变形,如图6所示是5种约束下的单位压力下的轴瓦径向变形云图,对应数值大小将计入到轴瓦油膜厚度中。研究结果表明:图5(a)中将轴瓦外圈固定而忽略轴承座计算轴瓦变形,轴瓦各个位置的径向变形相同;图5(b)中将轴瓦与轴承座视为一体且四周固定计算轴瓦变形,在轴瓦4个方形区域为多个载荷引起的变形叠加,导致变形较大(如图6(b)中A、B、C、D位置);图5(c)中由于该处悬置刚度较低,最大变形位置出现在未约束中间位置(如图6(c)中E位置);当将轴瓦与轴承座之间的关系变为接触时,轴瓦变形分布未发生变化,如图6(d)、(e)所示。

图5 5种不同约束条件下轴瓦弹性变形计算模型
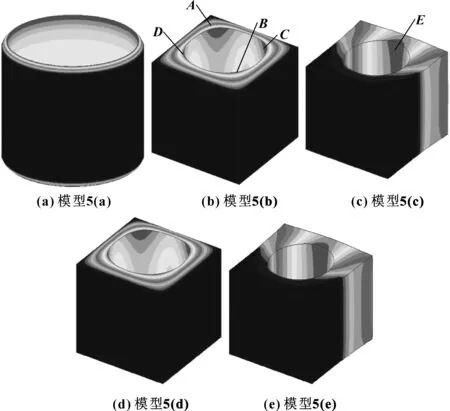
图6 5种约束下的单位压力变形云图
在油膜压力的作用下,轴瓦表面均会出现弹性变形,弹性变形会影响油膜厚度,油膜厚度大小又影响油膜压力。因此,该过程是一个耦合迭代过程。考虑轴瓦弹性变形后,轴瓦实际油膜厚度方程为
h=h0+δrs
(21)
(22)

采用有限差分方法计算修正后的油膜厚度下的油膜压力,反复循环迭代,直到收敛。
3 求解过程
3.1 不对中-轴颈润滑分析参数
为深入研究轴瓦弹性变形对轴承润滑性能影响,基于表1所示的轴承参数开展轴承性能分析。
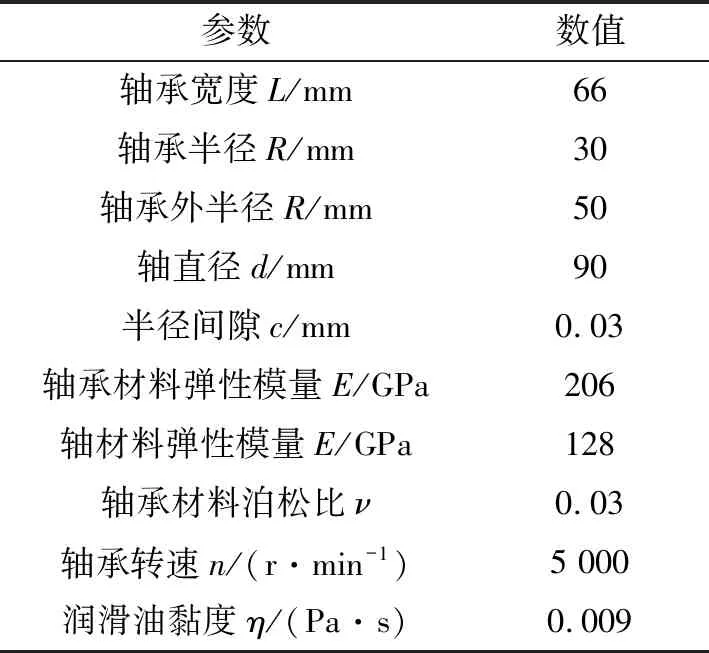
表1 轴承主要参数
3.2 计算流程
考虑到数值分析过程中计算轴瓦径向变形的网格与有限差分网格密度差异,运用二维插值算法将径向变形带入到有限差分网格对应节点上。即在考虑弹性变形的情况下,对变形矩阵进行插值处理,将6411节点矩阵,利用线性插值的方法变成110100的节点矩阵,使有限元网格的节点与油膜有限差分网格的节点进行相互对应。图7所示为考虑弹性变形时轴承性能的计算流程。
求解过程中为了获得稳定油膜压力,采取了超松弛迭代方法,松弛因子ω=0.1。油膜压力p可以表示[10]为
p=ωpnew+(1-ω)pold
(23)
判断新旧油膜压力的收敛条件
(24)

图7 计算流程图
4 计算结果与分析
4.1 不同模式下轴瓦变形
图8所示为单位压力作用下轴瓦径向的变形量。在油膜压力作用下轴瓦产生变形,采用变形矩阵的方法,分别在图4所示3种模型的内侧施加1 MPa单位荷载,同时在外侧施加全部约束和一半约束(如图5所示),计算出单位压力作用下轴瓦的变形量。如图8(a)所示,模型5(a)中在轴瓦的两端部变形较大,沿周向变形均匀,最大变形为4.8×10-8m。如图8(b)所示,模型5(b)中可明显看到4次变形波浪,波峰值位于轴承的4个角部位置,此时的变形大于仅考虑轴瓦的轴承。图8(c)所示为模型5(c)在半约束条件下轴瓦和轴承座视为一体时变形量,其最大变形量为6.1×10-7m,明显大于模型5(a)和5(b)的变形量,较大变形量是由于悬置部分刚度太低。当轴瓦和轴承座采用接触关系计算变形量时,轴承的变形分布未发生变化,变形的幅值变化较小,如图8(d)、(e)所示。
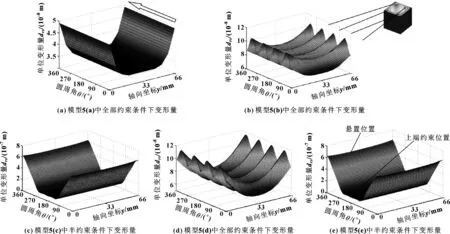
图8 单位压力作用下轴瓦弹性变形量
4.2 不对中轴颈-轴承油膜厚度
图9分别示出了未考虑轴瓦变形和仅考虑轴瓦变形而忽略轴承座时的油膜厚度分布(ε=0.7,n=5 000 r/min,φ=π/2,α=π/2,c=0.03 mm,μ=0.009)。结果表明:2种情况下轴承的油膜厚度分布变化差异较小,由于油膜压力使得轴瓦产生弹性变形,从而使最小油膜厚度hmin增大,但是油膜厚度未发生特别明显的增加。
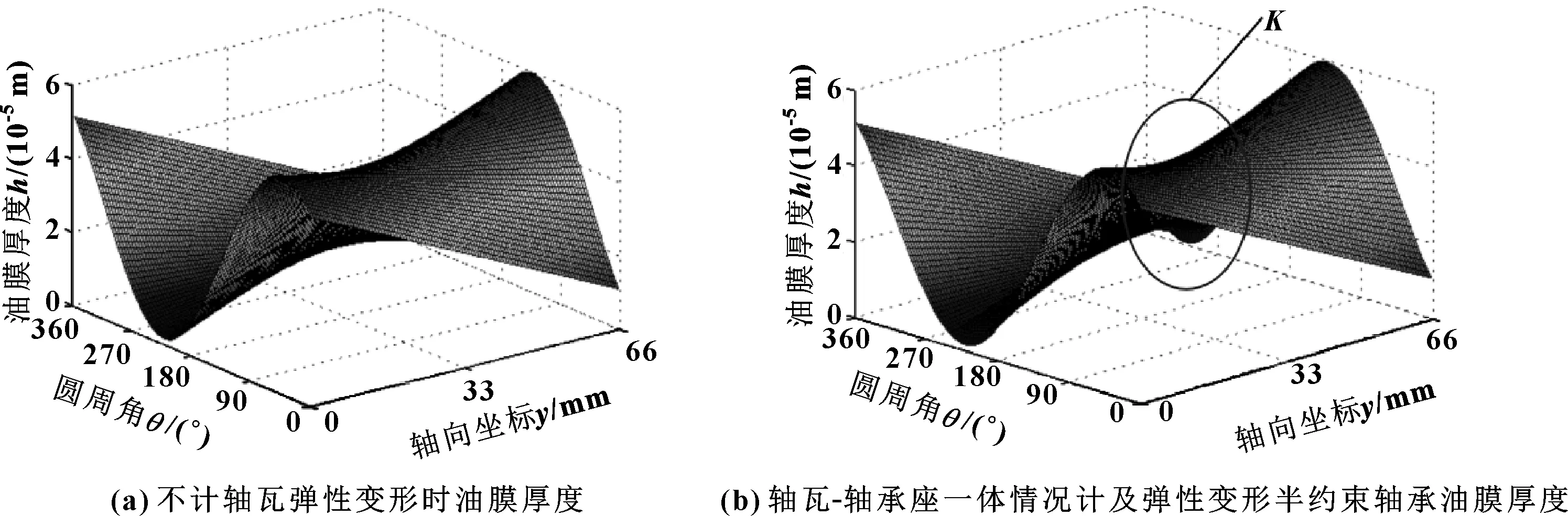
图9 计及和不计及弹性变形的油膜厚度分布
为了更深入地研究不同轴承弹性计算模型下油膜厚度情况,对比分析了轴承轴瓦接触条件下全约束和半约束条件下油膜厚度差值、轴承轴瓦一体条件下全约束和半约束条件下油膜厚度差值,如图10(a)和图10(b)所示,研究结果表明,在F和G位置油膜厚度差较大,接触和一体轴承座和轴瓦关系油膜厚度差异不大。如图10(c)所示为全约束条件下轴承座-轴瓦一体与轴承座-轴瓦接触模型下油膜厚度差值,研究结果表明,在承载区域中间位置(图10(c)中H位置)为正值,在承载区域中间位置(图10(c)中M、N位置)为负值。
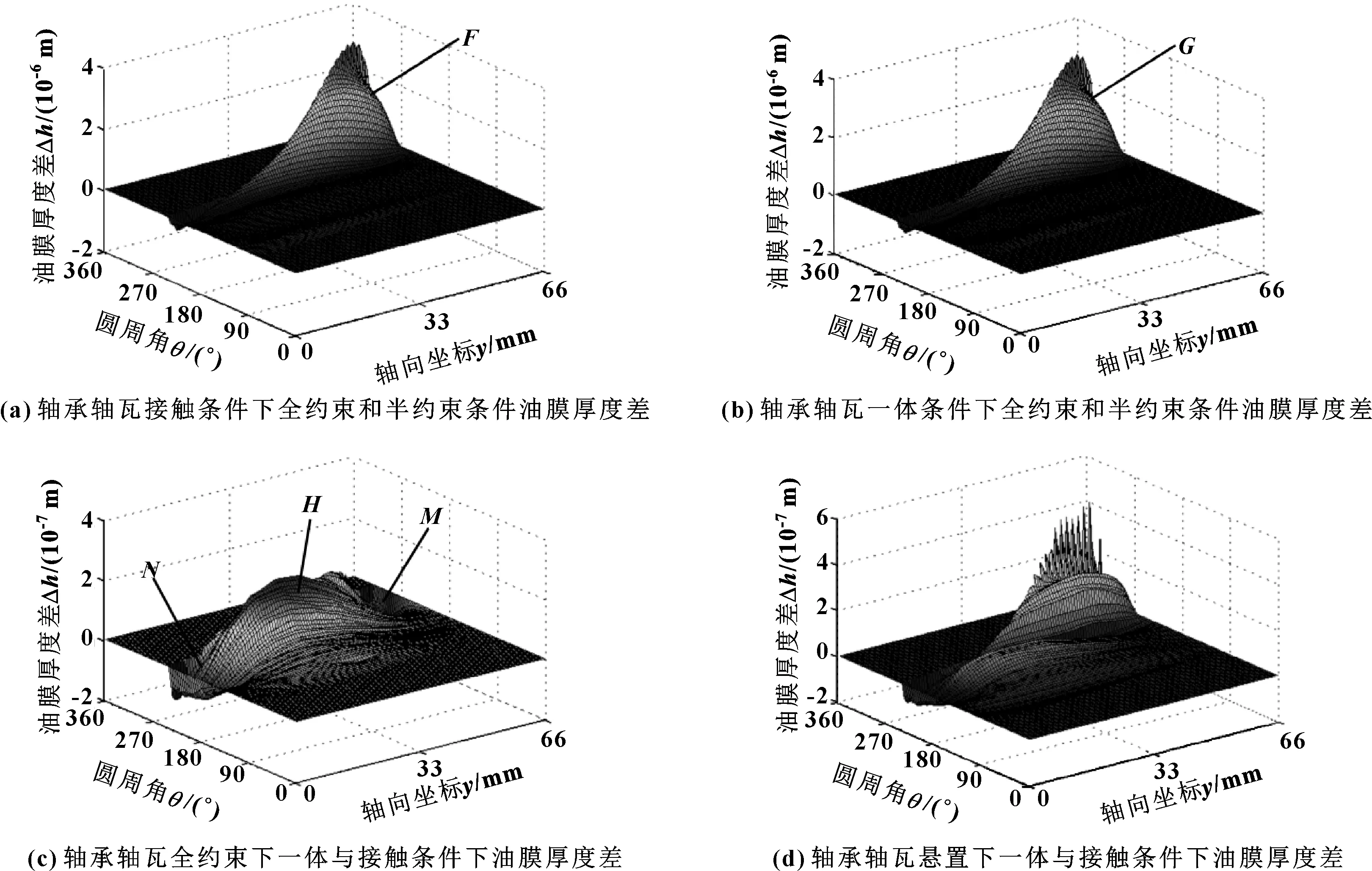
图10 5种不同约束模型的油膜厚度差异
4.3 不对中轴颈-轴承油膜压力
图11所示为不考虑轴瓦弹性变形和5种考虑轴瓦弹性变形下油膜压力分布。在分析过程中当偏心率ε较大时,较大的油膜压力对轴瓦变形影响较大,对最大油膜压力pmax的影响也较为明显,为此文中分析轴承在高速重载环境下轴承变形对油膜特性影响(ε=0.7,n=5 000 r/min,φ=π/2,α=π/2,c=0.03 mm,μ=0.009)。图9(a)所示为未考虑轴承变形下轴承油膜压力分布情况,φ=π/2使得油膜在轴承两端部出现较大压力(出现两峰值),pmax=85.525 MPa。图9(b)所示为轴瓦外圈固定且忽略轴承座支撑时的油膜压力分布,pmax=38.95 MPa,误差达到46.575 MPa。图9(c)所示为轴承机座全部固定且轴瓦与轴承座为一体时的油膜压力分布,pmax=28.46 MPa,误差达到57.065 MPa。图9(d)所示为轴承机座悬置固定且轴瓦与轴承座为一体时的油膜压力分布,pmax=30.69 MPa,误差达到54.835 MPa。图9(e)所示为轴承机座全部固定且轴瓦与轴承座为接触关系时的油膜压力分布,pmax=28.36 MPa,误差达到57.165 MPa。图9(f)所示为轴承机座全部固定且轴瓦与轴承座为接触关系时的油膜压力分布,pmax=30.23 MPa,误差达到55.295 MPa。研究结果表明:油膜压力的分布情况并未发生改变(但悬置轴承的最大油膜压力出现在另一侧),当偏心率较大时,油膜压力大幅度减小。由于油膜压力使轴瓦产生弹性变形,使得最小油膜厚度变大,使得与不计弹性变形相比最大油膜压力明显减小。

图11 5种不同约束模型的油膜压力分析
4.4 不对中轴颈-轴承润滑特性
图12所示为计及和不计轴瓦弹性变形时轴颈倾斜状态下(n=5 000 r/min,φ=π/2,α=π/2,c=0.03 mm,μ=0.009),轴承最大油膜压力pmax、最小油膜厚度hmin、端泄流量Q、稳定工作力矩M、承载力F随偏心率ε的变化关系。研究结果表明:未考虑轴瓦变形时会在不同偏心率下低估pmax、Q、M和F的值;当偏心率较低时,由于油膜压力较小,导致轴瓦变形较小,变形量对油膜厚度贡献量较小,不计和计及弹性变形时5种工况下的最大油膜压力、稳定力矩、轴承承载力相差不大,但是端泄流量相对于不计弹性变形时有较大的变化;当偏心率增加到一定数值(ε=0.7)后,油膜厚度随之变小,且不同约束模型对于油膜厚度影响较大,最大油膜压力在偏心率ε=0.5后突然变大,不考虑弹性变形油膜压力pmax明显大于考虑弹性变形时的油膜压力;但是端泄流量Q、稳定力矩M、承载力F等不计弹性变形的数值明显小于考虑弹性变形时的数值,其中模型5(a)的端泄流量、稳定力矩、承载力最大,且模型5(b)和模型5(d)全部约束情况下的端泄流量、稳定力矩、承载力,相比模型5(c) 和模型5(e)半约束情况下都增大,而对于最大油膜压力,模型5(b) 和模型5(d)略小于模型5(c) 和模型5(e)。全部约束和半约束在最大油膜压力pmax、端泄流量Q、稳定力矩M、承载力F方面相差不大。
图13所示为偏心率ε=0.7时轴承-轴颈最大油膜压力pmax、最小油膜厚度hmin、端泄流量Q、稳定工作力矩M、承载力F随转速n的变化关系。研究结果表明:随着转速增加,hmin、Q、M、F都呈增加的趋势;低转速时,考虑和未考虑弹性变形的各轴承性能参数相差不大,随着转速增加,Q、M、F差异增加;不考虑弹性变形的最大油膜压力明显大于考虑弹性变形时的油膜压力; 高转速时,考虑弹性变形与不考虑弹性变形Q相差不大;不考虑弹性变形时稳定力矩M、承载力F明显大于考虑弹性变形的数值。
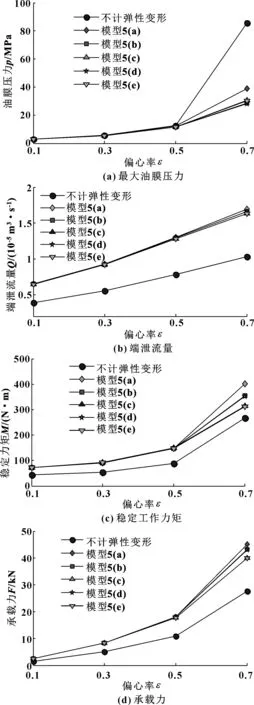
图12 不同工况下计及与不计及变形时轴承性能

图13 润滑特性随转速变化
5 结论
(1)不同的轴承约束形式对于轴承径向变形影响较大,轴瓦-轴颈视为一体和轴瓦-轴颈接触关系对于轴承润滑性能预测误差较小,可用轴瓦-轴颈一体关系进行轴承性能分析。轴瓦固定和轴瓦一半悬空2种状态下,对轴承性能的影响不明显。在偏心率较高时,润滑性能差异较大,若要精确预测性能应考虑模型差异。
(2)轴颈在轴承孔中倾斜时,对轴承最大油膜压力、最小油膜厚度有明显的影响,将轴瓦-轴承座考虑为一体和接触关系对于最大油膜压力影响较小,对油膜压力和油膜厚度的分布情况影响较小。
(3)未考虑轴瓦变形会在不同偏心率下低估pmax、Q、M和F,当偏心率较低时,由于油膜压力较小导致的轴瓦变形较小,变形量对油膜厚度贡献量较小,不计和计及弹性变形的5种工况下的最大油膜压力、稳定力矩、轴承承载力相差不大,当偏心率增加到一定数值后(ε=0.7),pmax明显大于不考虑弹性变形时的最大油膜压力。
