一维定态薛定谔方程的理论求解及MATLAB的仿真实现研究

王文慧

摘 要：量子力学的提出可谓是20世纪物理学上一个划时代的里程碑。经过一百多年的历史证明，量子物理学说明了物质属性及其微观结构这个根本性问题，同时也促进了一些高科技产业的发展。简述了量子力学的发展历程。在理想无限深方势阱下对一维定态薛定谔方程使用两种求解方法，一种是传统的理论求解，适用于简单势阱下的粒子运动;另一种是借助MATLAB软件进行特解求解，适用于复杂的势阱情况。为了全面描述粒子的运动状态，结合概率密度函数和概率分布函数来进行描述，适用于多个势阱条件。

关键词：量子力学;薛定谔方程;无限深方势阱;MATLAB

中图分类号：TB     文献标识码：A      doi：10.19311/j.cnki.1672-3198.2019.14.098

1 绪论

经典力学中以牛顿运动定律为基础的部分作为力学的一个分支最早被认为是力学的基本纲领。原因是牛顿运动定律能很好地解释宏观生活中的许多物理现象，被人们广泛接受与认可，具有很强的实用性。例如，人们根据牛顿的理论预测并发现了海王星。然而十九世纪以来，随着人们对物理学研究的不断深入，经典力学的局限性也逐渐显露出来。例如黑体辐射，英国物理学家瑞利根据经典统计力学和电磁理论推导出黑体辐射的能量分布公式仅适用于长波，发现短波部分与实验的反差严重，这一现象被称为“紫外灾难”。出现的问题还有光电效应中的红限频率，比热困难等等。这些问题的出现激励着物理学家不断的进行思考、实验，推动了相对论和量子力学的诞生。

利用普朗克的量子假说与爱因斯坦提出的光量子概念得出的普朗克-爱因斯坦关系式可以很好地解释了黑体辐射，光电效应以及康普顿效应。波尔的量子论可解释氢原子能级及线状光谱。德布罗意波的提出，指明当波长与客观尺寸相比拟时，波动性就显得很重要。因此在微观世界中，不能使用经典力学分析，只能使用波动力学。薛定谔方程（Schrdinger equation）是将德布罗意波的概念和波动方程相结合建立的二阶偏微分方程，由奥地利物理学家薛定谔提出。薛定谔方程表明在量子力学中，粒子以概率的方式出现，其正确性只能靠实验来决定。可以描述微观粒子的运动，每个微观系统都有一个相应的薛定谔方程式，通过解方程可得到波函数的具体形式。当势函数不随时间变化时，粒子具有确定的能量，粒子的状态称为定态。本文主要研究定态下一维薛定谔方程的求解问题。

目前量子力学的研究，推动了晶体管，能量回收，量子密码等领域的发展，使随机数发生器，量子计算机，瞬时通信，远距传输等成为可能。

此外本文还使用MATLAB软件进行了结果的形象化处理，其高效的计算能力，让求解薛定谔方程从繁杂的数学运算分析中脱身。其次，MATLAB具有很强的图形处理功能，实现计算结果可视化。

2 薛定谔方程

随着物理学研究的不断深入，经典力学开始遇到困难。如关于热辐射经典统计理论，1893年，威廉·维恩提出一个数学公式ρνdν=C1ν3e-C2ν/Tdν 此公式在光谱的短波部分的测定值与计算值完全一致，然而却不适用于中波，长波部分。1900年，英国物理学家瑞利根据经典统计力学和电磁学理论，推导出黑体辐射的能量分布公式为ρνdν=8πc3kTν2dν 而此式只适用于长波，在短波部分是无穷值，E=∫SymboleB@

0ρνdν=8πc3kT∫SymboleB@

0ν2dν→SymboleB@

可相反的是实验得出结果是零。这个反差强烈的严重问题，被称为“紫外灾难”，令许多物理学家感到费解。

十九世纪末，赫兹和汤姆孙在验证电磁波和发现电子的实验中也遇到了困难。经典物理学理论被一些实验结果推翻：不仅逸出電子的最大初动能与光强无关，存在红限频率，而且光电子几乎是瞬时逸出的。经典的比热理论也遇到了一些困难：杜隆-珀蒂定律CPCν=3R只适用于常温实验条件下;束缚态电子为何对比热贡献可以忽略不计;为何在常温下，大多数双原子分子和多原子分子振动自由度会被冻结，对比热也没有贡献。

经典物理学中遇到的种种困难推动了量子理论的发展。在1900年，普朗克提出一个经验公式，非常符合黑体辐射的实验结果。总结普朗克的量子化理论，黑体和辐射场交换能量只能以吸收或者发射“量子”的方式进行，以ε单位吸收或发射，能量保持不连续的变化。 1905 年，爱因斯坦普朗克能量子的假说进行进一步解释，提出了光量子的概念：假定光是由光子组成的粒子流，每个光子的能量的计算方法为ε=hν，其中，，ν表示光的频率，h是普朗克常数。而后，德布罗意对波粒二象性和德布罗意波的提出为量子力学的建立做出了极大贡献。

德布罗意觉得“任何物质都伴随以波，而且不可能将物质的运动和波的传播分开”。那么我们如何去发现呢？由λ=hmv可知对于宏观物体物质波几乎微不可察，而在微观世界，粒子与相应的德布罗意波长可相比拟，波动性才显著，这时不能使用经典力学分析，只能使用波动力学。

波函数的形式可以表示为：

φ（r→，t）=ei（p→·r→-Et）/h（1）

其中 r→表示位置，是矢量 ;t表示时间，为标量;p→和E分别表示粒子的动量和能量;h为约化普朗克常数。式（1）对时间求导：

φ（r→，t）t=φ（r→，t）·（-iEh）ihtφ（r→，t）=Eφ（r→，t）（2）

式（1）对r→求导：

-ihSymbolQC@

φ（r→，t）=p→φ（r→，t）-h2SymbolQC@

2φ（r→，t）=p→2φ（r→，t）（3）

（SymbolQC@

为拉普拉斯算子）

由E=p→22m及式（2）（3）得：

（iht+h22mSymbolQC@

2）φ（r→，t）=（E-p→22m）φ（r→，t）=0（4）

ihtφ（r→，t）=-h2SymbolQC@

22mφ（r→，t）（5）

考虑势场V（r→）中运动的粒子，根据经典粒子的能量关系式：

E=p→2/2m+V（6）

将式（6）代入（4）可得：

ihtφ（r→，t）=（-h22mSymbolQC@

2+V）φ（r→，t）（7）

此为薛定谔在1926年提出的方程，揭示了原子世界中物质运动的基本规律。

3 无限深方势阱下求解薛定谔方程

3.1 一维定态薛定谔方程

设粒子质量为m，沿x方向运动，势能为V（x），可得此时薛定谔方程为ihtφ（x，t）=-h22m·2x2+V（x）φ（x，t）（8）

定态即具有一定能量E的状态，定态下波函数形式为：

φ（x，t）=φ（x）e-iEt/h（9）

将（9）代入到（8），φ（x）满足如下能量本征方程：

-h22m·d2dx2+V（x）φ（x）=Eφ（x）（10）

d2dx2φ（x，t）+2mhE-V（x）φ（x，t）=0

令f（x）=2mhE-V（x）则一维定态薛定谔方程的形式为：

d2dx2φ（x，t）+f（x）φ（x，t）=0

3.2 无限深方势阱通解的理论推导

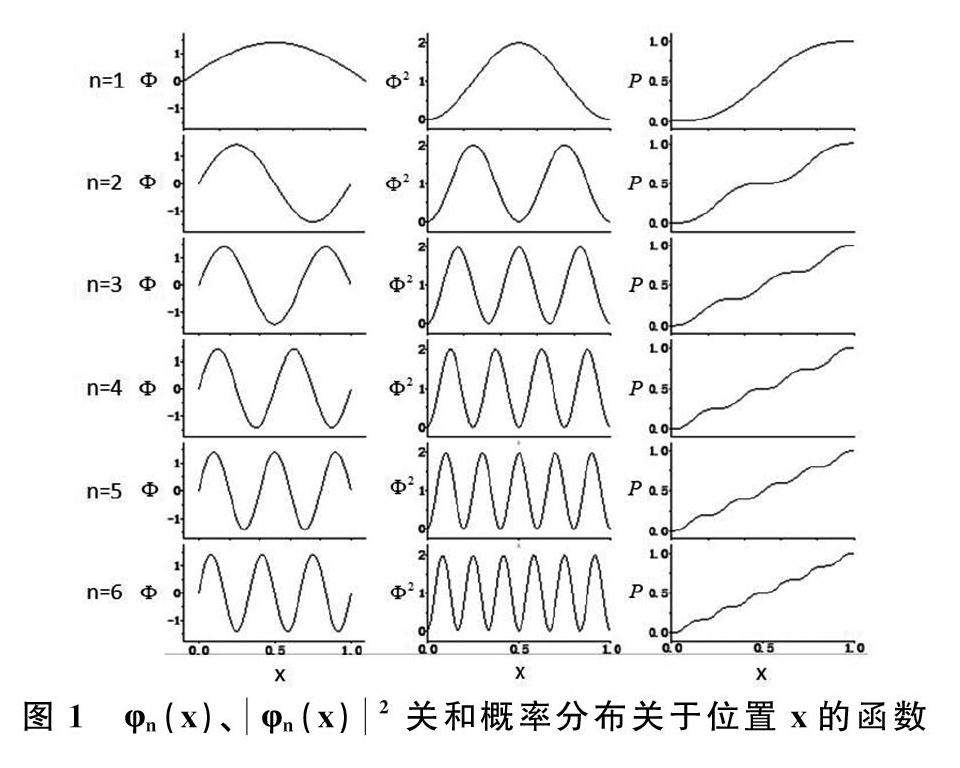
在理想无限深方势阱中 V（x）=0，0

，xa，当0

令k=2mEh2代入（11）此时（11）式可化为φ（x）=Asin（kx+φ）的形式。由于理想条件下，粒子穿透阱壁的可能性為零，所以φ（0）=0φ（a）=0，由上式可解得：

φ=0sinka=0，所以ka=nπn=1，2，3……

对于En能级波函数记为φn（x） 则 φn（x）=Ansin（nπax）（12）

利用归一化条件∫a0φn（x）2dx=1∴An2=2aAn=2a，将An=2a代入（12）得归一化的波函数为φn（x）=2asin（nπax）。

上文已经求解出函数φn（x）及φn（x）2的形式，是普通的正弦函数形式，接下来通过MATLAB进行数值模拟，形象化表示出在不同位置粒子出现的概率。φn（x）和φn（x）2在不同n值情况下的函数图如图一所示，左侧一列是φn（x）的函数图，中一列是φn（x）2的函数图，从第一行到最后一行分别是n=1，2，3，4，5，6。对于左侧这列图像，可以看出，几乎都均匀分布在φ=0的两侧，而对于φn（x）2表示概率密度的这条函数曲线表达的是当前位置出现粒子的概率大小。

3.3 MATLAB求无限深方势阱的特解

MATLAB软件功能非常强大，对于微分方程的求解方面也有相应函数可以解决，对于一个未知的变量连同它自己的微分变量由一个方程联系起来的关系就称之为微分方程，如一维定态薛定谔方程即为二阶微分方程，因为有二次微分项。无限深势阱中的薛定谔方程的形式为：

d2dx2φ（x，t）+kφ=0（13）

k=2mEh2其中，想要快速求解这个二阶微分方程，在这里我们假定势阱边界a=1，n=1，k=π，这样可以使用MATLAB求解方程的函数dsolve函数，此函数可以直接将需要求解的方程写入，dsolve（‘微分方程，自变量），例如：y=dsolve（'D2y+（pi^2）*y=0'，'x'），这个语句可以获得一个通解：y =C1*exp（（-k）^（1/2）*x） + C2*exp（-（-k）^（1/2）*x），其中C1和C2根据不同的初始条件就可以给定不同的数值;另外dsolve函数还可以直接给定初始条件来确定所求微分方程的特解，dsolve（‘微分方程，初始条件1，初始条件2，自变量），在无限深势阱中，边界的y都为0，求解函数可以写为y=dsolve（'D2y+（pi^2）*y=0'，'y（0）=0'，'y（1）=0'，'x'），运行之后得到的解为y =C3*sin（pi*x），根据薛定谔方程的归一化条件，可以很快求解出C3=2。无限深势阱条件下的薛定谔方程的特解为φ1（x）=2sin（πx）。使用MATLAB求特解需要注意的是需要使用sym类型将方程中的自变量和因变量声明为符号变量，才可以顺利的得到结果。

3.4 无限深势阱条件下粒子位置的概率分布

上文根据理论推导方法和借助MATLAB软件求特解的方法求出了无限深势阱中粒子分布的概率密度函数（图1中间列所示），这个图可以清晰的描绘出粒子落在区间中的概率高低，概率密度值越大，代表粒子出现的概率越大，而粒子落在某个区域的概率并不能从概率密度函数图中直观的看出，这时我们就需要计算概率密度函数的概率分布函数，这个函数一般是来刻画某个随机变量m小于某一数值x的概率，在这里我们假设概率分布函数用P来表示，P（x）指的是粒子出现的位置小于x的概率，概率分布函数就是概率密度函数的积分，在MATLAB中可以直接使用函数int来进行计算，计算结果如图1最右一列表示。从图中可以看出每条曲线的x=1对应的概率值都为1，对应了薛定谔方程归一化的性质。

另外这六条曲线中，总会出现一定的平台，这些平台说明，对应位置粒子出现的概率几乎为0，对应概率密度函数的最低点。若使用电子束来模拟粒子，则平台出现的位置就是暗条纹出现的位置，斜率越大，条纹越明亮。使用概率密度函数结合概率分布函数这样的分析方法，对复杂势阱的分析理解将会有一定的帮助。

4 结论

本文通过对经典力学的局限性的介绍，引出了物理学家对这些局限性问题的研究并提出了相对论和量子力学。另外，本文以无限深势阱为例，给出两种求解方式一种是传统的理论计算，使用于简单势阱下的求解，对于比较复杂的势阱，不具备理论求解的条件下，可以使用MATLAB软件来进行求解。对于理解势阱中粒子的分布位置，一般都是使用概率密度函数来分析，本文通过MATLAB软件求解出概率密度函数对应的概率分布函数，更加直观的获得粒子位置的概率信息，验证了解的形式与性质，对于复杂势阱中粒子运动状态的研究具有深刻的意义。

参考文献

[1] 林洽武.求解定态薛定谔方程的有限差分法[J].广东第二师范大学学报，2013.

[2] 苏汝铿.量子力学[M].北京：高等教育出版社，2002.

[3] 王忆峰，唐利斌.通过有限差分和MATLAB矩阵运算直接求解一维薛定谔方程[J].红外，2010.