并联电路E类逆变器软开关特性研究

梁奋强， 黄靖，黄晓生， 刘丽桑， 林抒毅， 孔毅鹏

(1. 福建工程学院 信息科学与工程学院，福建 福州 350118；2. 福建省工业集成自动化行业技术开发基地，福建 福州 350118)

磁耦合谐振式无线电能传输相比于传统的电能传输方式，更加的安全便捷，已经成为当前的研究热点。自从2007年美国麻省理工学院的Marin Soljacic等人采用磁耦合谐振式无线电能传输[1]，实现了中距离高效率的无线电能传输，同时使得无线电能传输应用在更多的场合。磁耦合谐振式无线电能传输具有传输距离远、传输效率高以及传输功率大的优点，但其高频供电电源的好坏，直接影响着整个系统的质量和效率[2-3]。E类逆变器由于其结构简单，高频高效，在理想的情况下效率可以达到100%，能够满足高频供电电源的要求，因此被广泛的应用于WPT(wireless power transfer)系统中。

根据负载网络的不同，E类逆变器分为并联电容E类逆变器、并联电路E类逆变器。这两种E类逆变器的负载网络不同之处，在于其输入电感参数的区别，并联电容E类逆变器中采用电感量足够大的扼流电感，能够使电感的纹波电流近似为零，使其输出直流电流；并联电路E类逆变器中则为电感值较小的并联电感，这可以实现在负载开路的情况下电路也能够实现软开关。现有的大量文献对于E类逆变器的分析都是基于并联电容E类逆变器，即假设采用足够大的扼流电感，并且在分析时忽略E类逆变器在高频状态下的寄生电容[4-5]，但是这样的设计适合于在较低频率的系统中，在高频状态需要考虑寄生电容这些重要的非理想因素，以避免出现次优化的设计。

文中基于并联电路E类逆变器进行分析研究。采用有限直流馈电电感的并联电路E类逆变器相比于采用无限大的扼流线圈的并联电容E类逆变器有明显的优点[6-8]，文献[6]通过分析表明采用较小的电抗代替LRFC扼流线圈能够输出更大的功率。在许多文献中，对于具有有限直流馈电电感的E类逆变器的设计采用长时间的迭代求解方法。采用合适的分析方法，便可推导出任何直流馈电电感值的E类逆变器的设计方案，文献[7]进行拉格朗日多项式插值获得明确的、可直接使用的设计方程，而不是迭代求解方法来求解，同时实现了更高的负载阻抗，得到更高效的输出匹配网络。文献[9]已经完成对于有限直流馈电电感的理想化E类逆变器的精确数学分析，并推导出电路元件与输入参数之间的关系式，而无需进行迭代计算。但是这些论文都是仅考虑了采用有限的直流馈电电感，并没有考虑系统在高频情况下，E类功率放大器寄生电容对于系统的影响，而且计算方法复杂。

在高频状态下考虑MOSFET的非线性漏-源寄生电容对于E类逆变器实现软开关导通十分重要。通常情况下，MOSFET的非线性漏-源寄生电容和连接在MOSFET漏极-源极之间的额外的线性并联电容提供总的并联电容。虽然在低频运行时额外的线性并联电容是起主导作用，但随着系统运行频率的升高，为了实现E类逆变器的软开关，总的并联电容的数值会大幅减小，而非线性寄生电容相对于总并联电容来说，所占的比例随着运行频率的增加而增加，所以在高频状态下E类逆变器的寄生电容对于E类逆变器实现ZVS(zero-voltage switching)和ZVDS(zero-voltage derivative switching)导通影响越来越明显。文献[10-12]对于E类功率放大器的分析就是基于MOSFET管的漏-源寄生电容是非线性元件进行的，从实验结果表明，考虑非线性的漏-源寄生电容对于实现E类功率放大器的ZVS、ZVDS导通十分重要。文献[13]表明仅仅考虑线性的寄生电容，不能够满足E类功率放大器的零电压导通条件，考虑非线性漏-源寄生电容Cds对于实现零电压导通十分重要。但是以上的推导及计算都是基于并联电容E类逆变器，而且考虑寄生电容表达式对于实际的电路参数计算十分复杂。由于寄生电容对于并联电路E类逆变器在高频状态下的实现软开关影响越来越大，文章分析了不同运行频率下，寄生电容对于E类逆变器实现软开关的影响。

本研究首先给出并联电路E类逆变器在理想状态下的参数设计方程。然后分别采用电荷充电原理和电容充能原理，推导出两个原理下不同的等效线性电容表达式。通过PSPICE MODEL求得寄生电容的等效电容，再采用PSPICE仿真，在1、4、13.56 MHz 3种不同频率下，分别对无寄生电容、两种不同的等效线性寄生电容这3个状态进行PSPICE仿真实验；最后搭建4 MHz的样机进行实验验证。

1 对于并联电路E类逆变器的分析

1.1 电路模型和假设条件

并联电路E类逆变器的电路拓扑图如图1所示，为简化分析并且满足随后的推导，做如下的假设：

(1)MOSFET管工作时视为一个理想的开关。即导通时阻抗为零，关断时阻抗无穷大，无导通或关断延时，占空比为50%。

(2)输出谐振电路的负载品质因素Q足够大，使得可以输出一个纯正的正弦波电流。

(3)电路中的器件均为理想器件，除负载R以外，其他部分均无损。

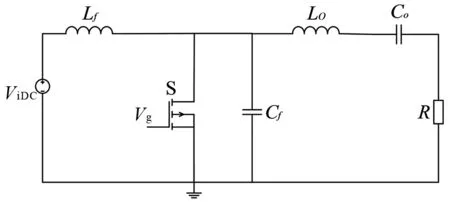
图1 基本电路模型Fig.1 Basic circuit model

图1中ViDC是输入的直流电源；Lf是输入电感；S是开关管；Cf是并联电容；Lo是谐振电感；Co是谐振电容；R是负载阻抗。通过调节并联电容Cf能够使得E类逆变器能够实现软开关。

1.2 理想情况下并联电路E类逆变器网络参数的推导设计

由图1可知，当谐振电路的品质因素Q足够大时，输出电流iR(θ)可假设为

iR(θ)=Imsin(θ+φ)

(1)

式中，iR为流过负载R的电流，θ为电流的相位，φ为电流的初始相位角。

谐振电路的有载品质因数Q为：

(2)

由谐振电路的谐振频率为：

(3)

联立式(2)、(3)，在有载品质因素Q以及运行频率确定的情况下，即可求出谐振电感Lo和谐振电容Co.

MOSFET的通断状态定义为如下：当相位在(0，π]区间时，开关S导通；当相位在(π，2π]区间时，开关S关断。在(0，π]区间时通过开关S的电流可以表示为：

(4)

式中ILf0是电感Lf在稳态周期的初始电流值。

在开关S由导通变为关断后，断开的瞬间开关S的电流转移到电容Cf，并开始对并联电容进行充放电。所以，在(π，2π]期间并联电容满足如下表达式，

(5)

式中vs是开关管S的电压。

由(5)式可得：

(6)

该式的通解如下：

vs(θ)=ViDC+C1cos(q·θ)+C2sin(q·θ)-

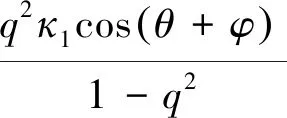
(7)

(8)

式中C1、C2为待求解的常数。q为谐振频率与工作频率比值。

然后使得E类功率放大器的运行同时满足ZVS与ZVDS的条件，即可推导出电路参数，即：

(9)

并且开关S断开瞬间电容Cf的电压为：

vs(π)=0

(10)

联立求解即可求得：

(11)

因此，在负载固定的情况下，当系统运行频率和品质因素固定时，即可求出Lf、Cf、Lo、Co。

1.3 非线性漏极-源极寄生电容的等效电容推导

E类逆变器总的并联电容是由额外的并联电容和MOSFET的寄生电容组成的。随着运行频率的升高，实现E类逆变器软开关的总并联电容减小。因此，MOSFET的漏极-源极之间的非线性寄生电容相对于总并联电容来说，所占的比例随着运行频率的增加而增加，所以在高频运行状态下不能忽略MOSFET的寄生电容。

MOSFET的非线性漏极-源极寄生电容可以由下面的非线性公式表示：

(12)

式中Vbi是内置电位，对于硅管典型值为0.5～0.9 V；vs是漏极和源极之间的电压；Cj0是vs=0时的结电容；M是等级系数，典型值为0.5。

在实际的电路设计中，非线性的电容很难准确考虑，因此考虑将漏极-源极之间的非线性电容等效成线性电容，这样便于在电路设计时相应的调整并联电容的大小，使得E类逆变器能够工作在理想状态。而对于MOSFET非线性寄生电容的等效线性电容的推导，采用两种不同的计算原理：1)基于电荷充电的原理；2)基于电容充能的原理。

根据电容的电荷充电原理可得：

(13)

通过求解可得：

根据电容的电容充能原理可得：

(15)

通过求解可得：

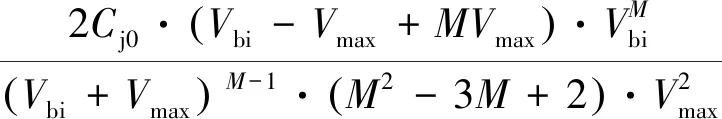
(16)

通过电荷充电的原理以及电容充能的原理，分别得到两个不同的等效电容方程。后面将通过仿真与实验来验证两种原理推导出的等效电容的合理性，为实际的电路设计提供理论参考依据。

2 仿真与实验

2.1 等效线性电容的计算

通过上述等效线性电容的推导公式可知，该等效线性电容的计算公式与系统的频率无关。本次仿真实验采用的MOSFET型号为SUD35N10-26P，通过SUD35N10-26P的PSPICE MOSFET models可知在计算等效电容时Cj0、Vbi、M的参数值。MOSFET的参数值如表1给出所示。

表1 MOSFET参数

首先求得通过电容的电荷充电原理得到的等效电容，将参数带入式(14)可得：

(17)

然后求得通过电容的电容充能原理得到的等效电容，将参数带入式(16)可得：

Ceq2=0.125 nF

(18)

2.2 仿真与分析

根据上述的系统设计方法，可以设计出在不同谐振频率下的E类逆变器的仿真电路参数。

2.2.1 1 MHz时的电路特性

当E类逆变器运行频率为1 MHz时，系统参数见表2。

表2 仿真电路参数

在考虑MOSFET的寄生电容时，额外的并联电容应相应的减小。当寄生电容为Ceq1=0.17 nF时，Cfeq1=Cf-Ceq1=3.823 nF; 当寄生电容为Ceq2=0.125 nF时，Cfeq2=Cf-Ceq2=3.868 nF。

由图2所示，在系统谐振频率为1 MHz，对比不考虑MOSFET的寄生电容和两种考虑寄生电容时MOSFET的漏极-源极电压VDS的波形。可以看出在3种不同的并联电容情况下，MOSFET均可实现软开关，但在考虑寄生电容时，对于MOSFET的软开关有一定的改善。

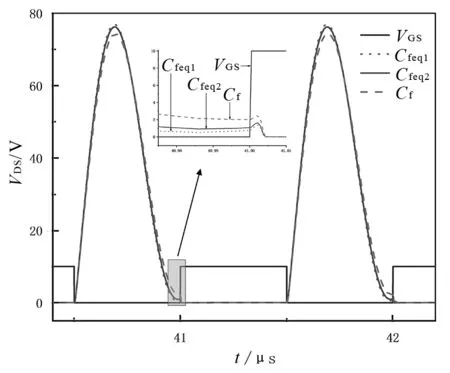
图2 频率为1 MHz时的VDS仿真波形Fig.2 VDS simulation waveforms at f=1 MHz

2.2.2 4 MHz时的电路特性

当E类逆变器运行频率为4 MHz时，系统参数见表2。

当寄生电容为Ceq1=0.17 nF时，Cfeq1=Cf-Ceq1=0.828 nF; 当寄生电容为Ceq2=0.125 nF时，Cfeq2=Cf-Ceq2=0.873 nF。

如图3所示，系统谐振频率为4 MHz，对比不考虑MOSFET的寄生电容和两种考虑寄生电容时MOSFET的漏极-源极电压VDS的波形。从图3可以看出，当不考虑MOSFET的寄生电容时，开关管为硬关断；考虑MOSFET的寄生电容时，若等效线性电容为Ceq2，按照并联电容为Cfeq2进行实验，能够有效改善开关管的关断状态；若等效线性电容为Ceq1，按照并联电容为Cfeq2进行实验，可以看到开关管在关断时，处在软开关状态。说明在高频状态下，如果不考虑MOSFET的寄生电容，会导致E类逆变器不能实现软开关。通过考虑等效的线性电容，极大地改善了E类逆变器的开关特性，且通过电荷充电原理计算出的等效线性电容，能够使得E类由硬关断转变为实现软开关，这也表明高频状态下考虑MOSFET的寄生电容的重要性。

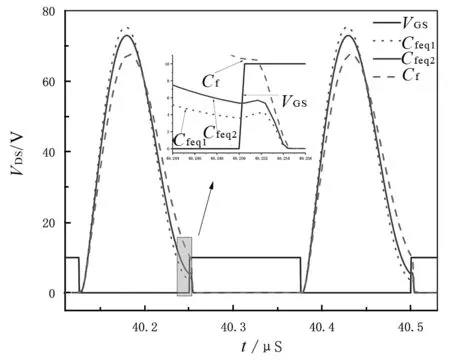
图3 频率为4 MHz的VDS仿真波形Fig.3 VDS simulation waveforms at f=4 MHz

2.2.3 13.56 MHz时的电路特性

当E类逆变器运行频率为13.56 MHz时，系统参数见表2。

当寄生电容为Ceq1=0.17 nF时，Cfeq1=Cf-Ceq1=0.124 nF; 当寄生电容为Ceq2=0.125 nF时，Cfeq2=Cf-Ceq2=0.169 nF。

如图4所示，在系统谐振频率为13.56 MHz，对比不考虑MOSFET的寄生电容和两种考虑寄生电容时MOSFET的漏极-源极电压VDS的波形。从图4可以明显看出，当不考虑MOSFET的寄生电容，按照并联电容Cf进行实验时，开关管为硬关断；考虑MOSFET的寄生电容时，若MOSFET寄生电容的等效线性电容为Ceq2，按照并联电容为Cfeq2进行实验，开关管关断时处在软开关状态；若等效线性电容为Ceq1，按照并联电容为Cfeq1进行实验，可以看到开关管关断时处在良好的软开关状态。实验结果表明高频时若不考虑MOSFET寄生电容的存在，会使得开关管处于硬关断；考虑寄生电容存在时，能够有效改善开关管的导通状态，且电荷充电原理计算出的等效线性电容更加精确。

图4 频率为13.56 MHz的VDS仿真波形Fig.4 VDS simulation waveforms at f=13.56MHz

2.3 实验与分析

根据系统的电路模型，搭建的实验装置如图5所示。结合实际的实验条件，采用4 MHz的谐振频率进行实验，具体的实验电路参数如表3所示。

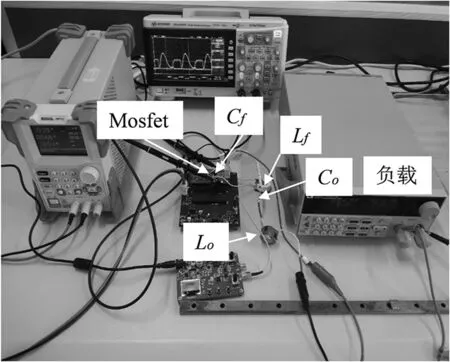
图5 实验装置Fig.5 Experimental setup

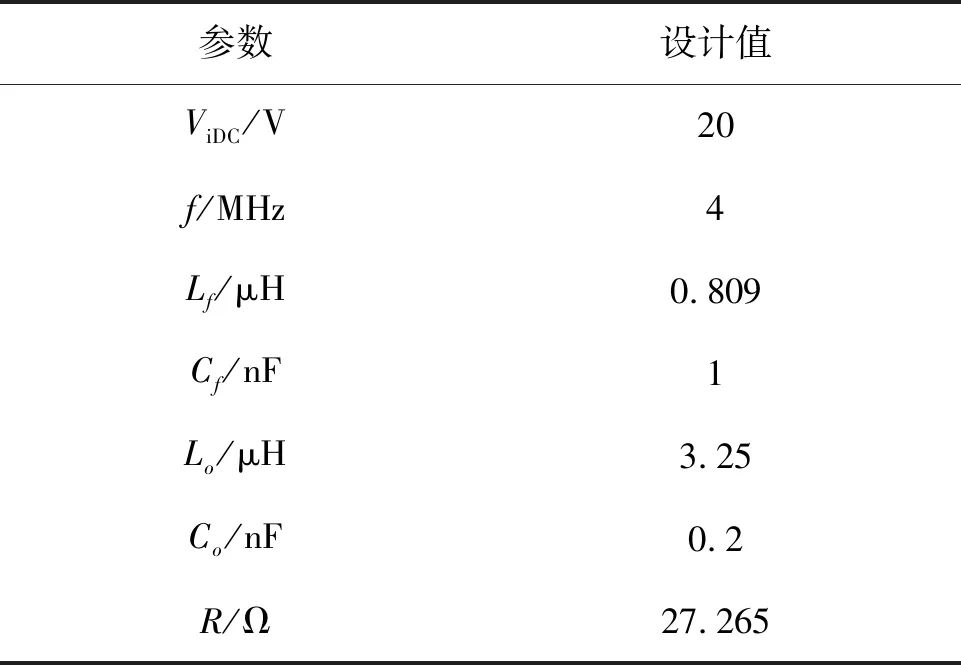
参数设计值ViDC/V20f/MHz4Lf/μH0.809Cf/nF1Lo/μH3.25Co/nF0.2R/Ω27.265

当寄生电容为Ceq1=0.17 nF时，实验采用的Cfeq1=0.82 nF; 当寄生电容为Ceq2=0.125 nF时，实验采用的Cfeq2=0.867 nF。

从图6(a)的实验波形可知，当不考虑系统的寄生电容时Mosfet不能实现软开关；从图6(b)、(c)可以看出，在实际电路设计中考虑寄生电容的存在时，能够使得Mosfet处在软开关状态，由于实际电路参数存在的误差，以及Cfeq1和Cfeq2相差很小，图6(b)、(c)的实验波形相差不大。由图6可知，实测波形与前面的仿真波形相符。

图6 不同并联电容下的实验波形Fig.6 Experimental waveforms under different shunt capacitances

3 结论

考虑了MOSFET在高频状态下存在的非线性寄生电容对于并联电路E类逆变器实现软开关的影响，通过两种不同的理论推导方法，将MOSFET的非线性寄生电容等效为线性电容。然后分别在1、4、13.56 MHz 3种不同的运行频率下，分别对无寄生电容、两种不同的等效线性寄生电容这3个状态进行PSPICE仿真实验；最后通过4 MHz的实验样机进行验证。通过计算分析以及实验验证，得到如下结论：

1)在高频状态下，寄生电容的影响越来越大，如果忽略MOSFET的寄生电容，仅仅采用理论计算电容，MOSFET软开关效果比较差,因此实际电路设计中应考虑等效线性寄生电容的存在，这样能够使得E类逆变器实现较好的软开关特性。

2)电荷充电原理是通过寄生电容充电时电荷量的变化来进行计算的，而电容充能原理，则是通过充电时电容中存储的总能量的变化来进行计算的。通过考虑基于电荷充电的原理和电容充能的原理推导所得的线性等效电容，对于并联电路E类逆变器实现软开关均有良好效果，但基于电荷充电的原理推导出的等效电容更加合理。