改进粒子群算法的双电机转速同步控制*

吴 杰，王 华，包伟刚

(南京工业大学 机械与动力工程学院，南京 210000)

0 引言

随着工业技术的发展，需要双电机同时驱动部件工作的场合日益增多，尤其是在高速数控剐齿机床中，刀具和工件间的转速同步性能的优劣将直接影响系统的可靠性与齿轮加工效果[1-2]。工程中单电机多采用结构简单、易于实现、性能良好的PI控制器[3]。而现在研究的双电机速度同步控制有这样几类控制结构：主从控制、并行控制和交叉耦合控制等[4-5]。

近年来刘燕等[6]设计了利用模糊方法的多电机同步控制，但是模糊规则的设定困难且缺乏一定依据。王建红等[7]建立了采用虚拟主轴的双电机同步控制，但没有对负载扰动下的电机同步性做研究。李莉等[8]采用两台电机的转速差乘以同一个耦合同步系数K补偿到电流环，但未考虑当电机参数不同时的转速补偿，且耦合参数通过试取法得到，效率低下，未达到理想的最优效果。

综上所述，本课题基于双电机同步控制缺乏高效的参数优化和采用相同耦合参数致使同步控制精度不足的缺点，在经典双PI并行控制的基础上，针对启动和有负载扰动时两电机具有转速同步误差的问题，改进传统并行交叉耦合方法，采用不同数值的耦合参数对两电机分别进行转速补偿，并利用改进粒子群算法优化同步控制系统的耦合参数。

1 双电机同步控制系统结构设计

双电机同步控制系统结构原理图如图1所示。

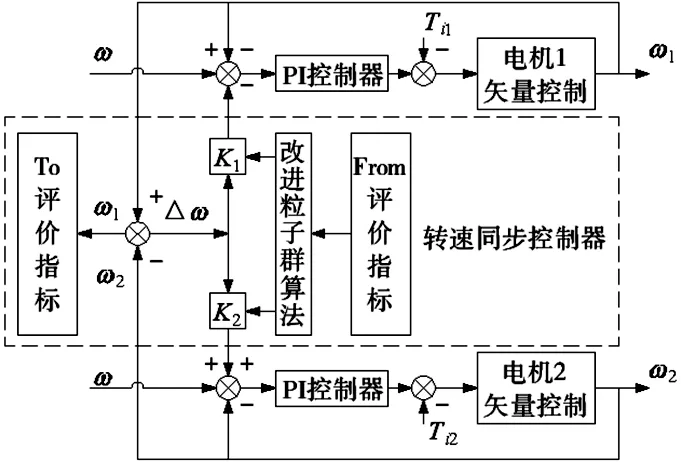
图1 双电机转速同步控制系统结构

图1中，ω为电机给定参考转速，Ti1、Ti2为负载转矩，ω1、ω2为两电机的实际转速，K1、K2为算法优化后的耦合参数值,单电机的PI控制器控制给定转速ω，双电机的转速同步控制器控制速度同步误差Δω。

从图1中可以看到，所设计的转速同步控制器没有将速度同步误差补偿到两电机的电流环，这是由于在实际工业应用场合，电机均采用与其相匹配的专用伺服驱动器来驱动，其电流环作为速度环的内环，它的参数在出厂时就已经整定在驱动器中，不宜改动。并且考虑到两电机的参数不一定相同，故未采用传统双电机交叉耦合同步控制以同一比例值(或PI值)作为速度耦合控制器直接补偿两电机的转速误差。新的转速同步控制方法是将两电机的速度同步误差乘以不同的耦合参数K1、K2分别补偿于两电机的速度环，以此来提高系统的实用性和速度同步性。

在设计完同步控制器后，就需要评价指标判定同步控制器的同步性能。而在双电机同步控制中希望两电机在遇到负载扰动时两电机能最快回复同步转速，因此选取离散化的时间绝对偏差积分ITAE[9]作为判别系统同步性能的评价指标，即：

(1)

式中，JITAE为评价指标的积分值；t为评价时间；e(m)为两电机同步误差。

在评价指标ITAE中，系统同步误差和时间变化可以引起较大的指标变化，因此将式(1)作为判别同步性能的权函数，可以较好的判定所取的耦合参数K1、K2在同步控制系统中的优异程度。

2 粒子群算法及其改进

粒子群优化(PSO)算法是Kennedy和Eberhart于1995年提出的模拟鸟群社会行为的一种优化算法[10]。算法初始化的随机解个体称为粒子，一个群落由i个粒子构成，群里的每个粒子代表优化问题的最优解。在PSO中，每一个粒子通过综合参考自身和邻域所遇到的最优位置，将自身定位为最优解。

虽然传统的PSO算法操作简单，通用性强，但有时易于陷入局部最优解，收敛速度在进化后期显著降低。为了提高目标参数优化的速度和准确性，提高速度同步控制器的同步性能，改进了传统PSO算法，增加了动态惯性权重和粒子突变，其设计方法如下。

2.1 动态惯性权重设计

采用线性微分递减权重，公式为：

(2)

式中，ω(t)为惯性权重；ωint为权重的初值；ωend为最大迭代时的权重；t为当前迭代次数。

由于粒子群算法的权重设置过大会提高系统的全局寻优性能，降低局部寻优性能，反之亦然。所以线性微分递减权重选取较大的值作为惯性权重的初始值，而较小的值作为惯性权重的最终值。通过该方法使ω在算法初期缓慢减小，加强了全局寻优能力，使算法可以很快找到合适的值，而ω在算法后期加快减小，提高了后期的局部搜索能力，因此可以加快算法的收敛速度，改善经典线性递减权重容易前期找不到合适的粒子导致后期陷入局部最优的缺点，提升算法性能。

2.2 自适应变异规则设计

为了解决粒子群算法过早收敛，而使粒子搜索范围变小，易陷入局部最优解的问题，本文引入如下变异规则：

(3)

虽然良好的动态惯性权重可以提高算法的精度和优化速度，但通过引入粒子突变，使种群中的每个粒子在迭代过程里都有机会变异，以此提高算法的全局搜索能力。

经历了以上两项设计，得到了一种新的粒子群优化算法，即改进粒子群优化(MPSO)算法。采用动态惯性权重来提高算法的精度和收敛速度，并通过粒子突变来增强算法的全局搜索能力，使得MPSO算法能在保证转速同步控制系统耦合参数K1和K2优化精度的同时更快得到优化结果。

3 转速同步控制系统仿真与实验

3.1 仿真过程与结果分析

为验证所提转速同步控制方法的控制效果，选取两台永磁同步电机，利用Simulink搭建转速同步控制系统仿真模型，并根据MPSO算法优化同步控制系统耦合参数的原理，在MATLAB中以M文件的形式编写相应的控制算法。

可以看到，仿真模型中两电机的同步误差与MPSO算法轮循。其轮循方法如图2所示。这样通过仿真模型与MPSO算法的轮循，实现转速同步控制器的不断寻优，其中仿真模型如图3所示。

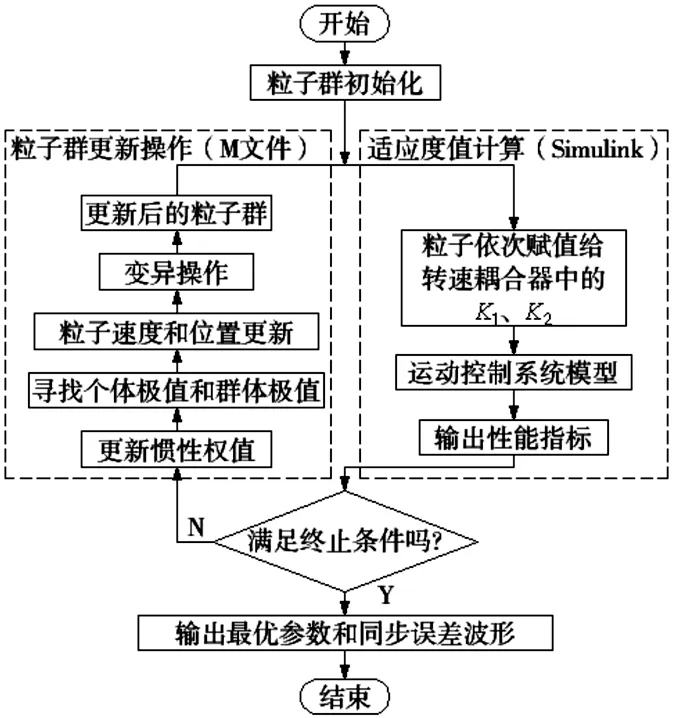
图2 系统仿真流程

图3 双电机转速同步控制系统仿真模型

从图3可以看出，转速同步控制器由系统同步性能指标计算模块、MPSO算法和基于交叉耦合原理的速度补偿模块组成。PMSM模型直接从Powerlib库中调用，相关参数见表1。

表1 永磁同步电机参数

另外传统PSO算法仿真设置参数如下：种群数为40，维数为2，加速度常数为2，速度范围为[-1,1]，惯性权值为0.6，最小适应值0.001,最大迭代次数50，耦合参数范围K1=K2=[0,100]，而MPSO算法更改了：初始权重0.9，最大迭代时惯性权重0.4，变异阈值C=0.9。在运行中，两电机参考转速1000r/min，在0.08s给系统突加10N的负载扰动，两种算法仿真过程如图4所示。

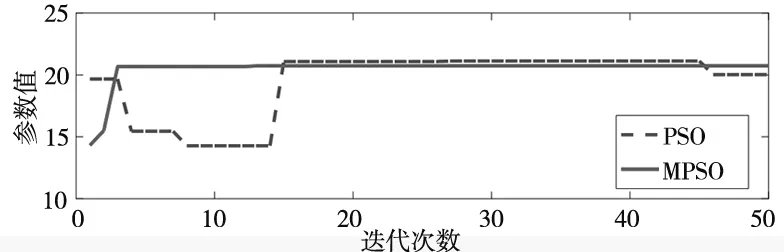
(a) 参数K1优化过程

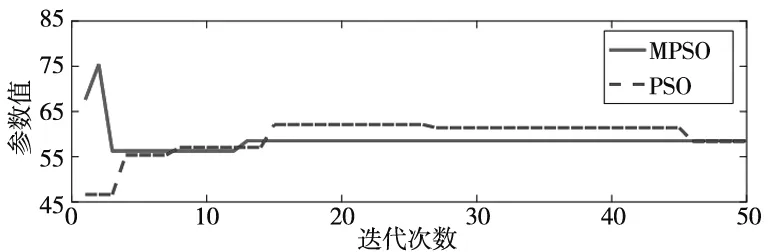
(b) 参数K2优化过程

(c) 适应度值进化过程

(d) 转速同步误差比较 图4 耦合参数K1、K2优化过程与结果

从图4c可以看出两种算法均使同步误差的适应度值逐步减小，使得两电机的转速同步性能逐渐提高。与此同时，由于MPSO加入了动态惯性权重设计和变异规则，在前14次迭代后就已经得到了最优解，而PSO迭代到第45次才得到最优解，大大提高了收敛速度。且MPSO最终适应度值小于PSO的最终适应度值，可见MPSO提高了收敛精度。在搜索范围上，虽然图4b中两种算法所取参数K2范围基本相当，但是图4a中MPSO所取参数K1约为[55,80]，PSO参数K1约为[50,55]，搜索范围提高了5倍，说明MPSO能在更大的范围内寻找最优解，提高了找到最优解的可能，这一点在图4c中MPSO算法适应度值的范围与精度都高于PSO算法得到了验证。

表2 仿真结果

从表2可知，采用PSO算法优化后K1和K2略小于MPSO算法优化后K1和K2，两种算法所优化后的同步误差波形图如图4d，可以看出，由于两电机参数不同，在启动时会产生一定同步误差，两种算法在克服启动同步误差的能力基本相同，而在受到10N的突加负载扰动时，MPSO在0.09s基本恢复稳定而PSO在0.095s恢复稳定，说明了MPSO算法进一步缩短了调节时间。为了更明显的表现MPSO转速同步控制系统的优异性能，将经典双PI并行同步控制策略与之相比较，如图5所示。

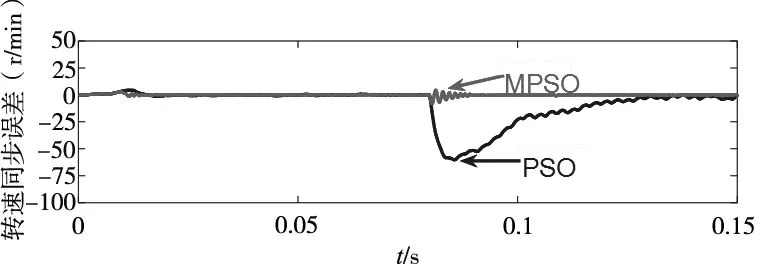
图5 两电机转速同步误差比较

可以看到图5中，由于传统双PI并行同步控制策略使两电机转速之间无耦合，所以当两电机参数不一致时，启动同步误差较大，启动精度为0.455%，当系统任意一电机受到突加负载而发生转速变化时，只能通过速度环PI调节器来跟踪给定参考转速，另一电机不会产生转速波动，因此产生较大的同步误差，其同步误差控制精度为6.213%。而在本文的双电机同步控制策略下，系统通过MPSO优化后的转速同步控制器对两电机分别进行速度环补偿，因此启动误差相比传统双PI并行同步控制策略明显降低，精度为0.302%，在突发负载扰动时同步精度大大提升，为0.845%。与此同时，MPSO优化后的系统不管在启动还是负载扰动时，调节时间都小于传统双PI并行系统。上述结果表明，MPSO算法优化速度远快于PSO，且同步精度略优于PSO,而相比传统双PI并行同步系统，不管是控制精度还是稳态回复速度都得到了大幅的提升。

3.2 实验与分析

根据研究需要，搭建了两电机同步实验系统，如图6所示。采用德国dSPACE的标准组件DS5202作为控制器来搭建实验平台，利用MATLAB/Simulink/RTW与dSPACE可直接连接的特点控制两电机，并通过上位机实验软件ControlDesk进行监控与记录。

(a) 实验原理图

(b) 系统实物图 图6 双电机转速同步控制系统

实验中，将MPSO优化后的耦合参数输入控制器，给定两电机参考转速均为1000r/min，电机1加负载扰动10N，电机参数见表1，实验结果如图7和表3所示。

(a) 双PI并行控制电机转速

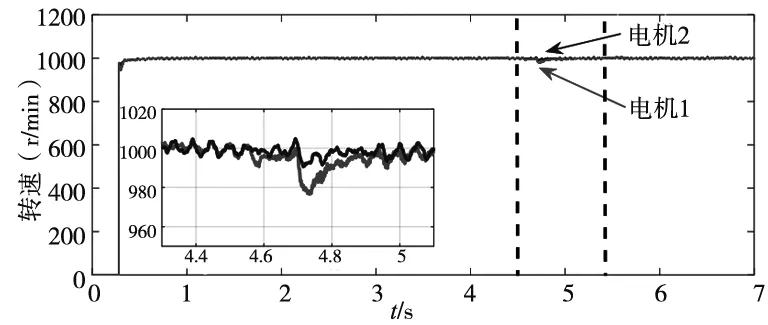
(b) MPSO同步控制电机转速

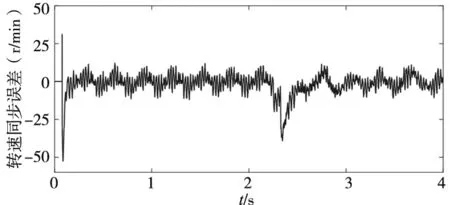
(c) 双PI并行控制同步误差

(d) MPSO同步控制同步误差 图7 系统突加负载转速波形

参数双PI并行控制MPSO同步控制启动同步误差(r/min)6030负载扰动最大同步误差(r/min)4016负载扰动转速波动(r/min)3822稳态同步误差(r/min)125

从图7a和图7b中可以看到，MPSO同步控制并不能减小单个电机的稳态误差，但是在系统出现负载扰动时，MPSO同步控制可以使两电机速度产生耦合，减小了转速波动和同步误差。在图7c和图7d中可以看到，不管在启动、有无负载扰动时，MPSO同步控制都减小了两电机的转速同步误差。综合图7可以得到表3的实验结果：在启动阶段，MPSO同步控制的同步误差相比双PI并行控制减小了50%。在系统受到负载扰动时，MPSO同步控制最大同步误差为16r/min，两电机的转速波动为22r/min，而双PI并行同步控制最大同步误差为40r/min，两电机的转速波动为38r/min。当系统稳定时MPSO同步控制稳态同步误差相比双PI并行控制减小了58.3%。通过分析以上结果可知，在MPSO同步控制方法下，两电机在有启动和无负载扰动时的转速同步误差都得到显著降低，且在有负载扰动时对单电机的转速波动也有了有效遏制，系统表现出优越的鲁棒性和动态响应能力。

4 结束语

(1)本文在经典双PI并行控制的基础上，针对启动和有负载扰动时两电机具有转速同步误差的问题，改进了传统并行交叉耦合方法，采用数值不同耦合参数对两电机分别进行转速补偿，提高了同步控制精度。

(2)通过改进的粒子群算法，进一步提高了参数优化速度，改善了同步性能，使系统无需人工经验即可得出参数优化值，提高了工作效率。

(3)仿真与实验的结果验证了所提转速同步控制方法可以改善系统的启动性能，提高系统的抗负载扰动能力和转速同步跟踪能力，有效降低了突加负载扰动时的同步误差。