混合励磁同步电动机控制策略与仿真分析*

夏永洪，仪轩杏，温子健，张景明，陈 瑛

(南昌大学 信息工程学院，南昌 330031)

0 引言

混合励磁同步电动机(HESM)是一种新型永磁电机，不仅具有永磁同步电动机的效率高、功率密度高的特点，而且具有电励磁同步电动机调磁方便的优点，因此在新能源电动汽车、航空航天领域具有广泛的应用前景[1-2]。

目前国内外对HESM本体研究已经做了大量的工作，提出了许多不同结构的混合励磁电机方案[3-4]。但是，在混合励磁同步电动机控制方面的研究相对还很少。文献[5]中提出了矢量控制和电流滞环分区控制策略；文献[6]中建立了基于通用坐标系的动态矢量控制模型，以及对隐极HESM提出了一种基于转子磁场定向的铜耗最小化矢量控制策略；文献[7]中根据HESM的参数特点，推导了最大转矩输出的必要条件，并提出了HESM的磁链控制策略。实际应用中，针对HESM的调速控制策略进行研究非常必要，其中最大转矩电流比控制和功率因数为1控制是常用的控制方法，然而，这些文献对这两种控制策略在HESM中的应用均没有进行研究。

为此，本文针对一种混合磁极式的混合励磁同步电动机控制策略进行研究，推导其数学模型，针对混合励磁同步电动机低速运行区提出最大转矩电流比控制策略，高速运行区提出功率因数为1的控制策略。基于MATLAB/Simulink软件，建立混合励磁同步电动机控制系统仿真模型，验证其控制策略的正确性。

1 HESM结构与与主要参数

混合励磁同步电动机在转子上增加了一个电励磁绕组，与永磁同步电动机数学模型相比增加了一个励磁变量[8]，可根据电动机实际运行情况分别对励磁电流和电枢电流进行协调控制。

本文所用混合励磁同步电动机的结构截面图如图1所示，其参数如表1所示。

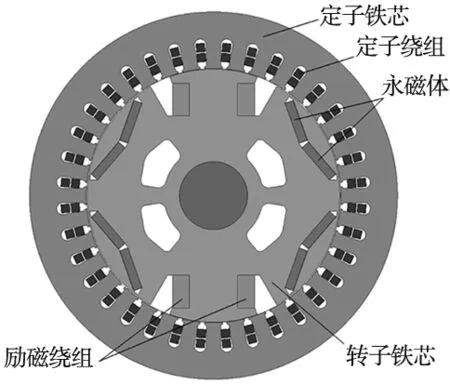
图1 混合励磁同步电动机截面图

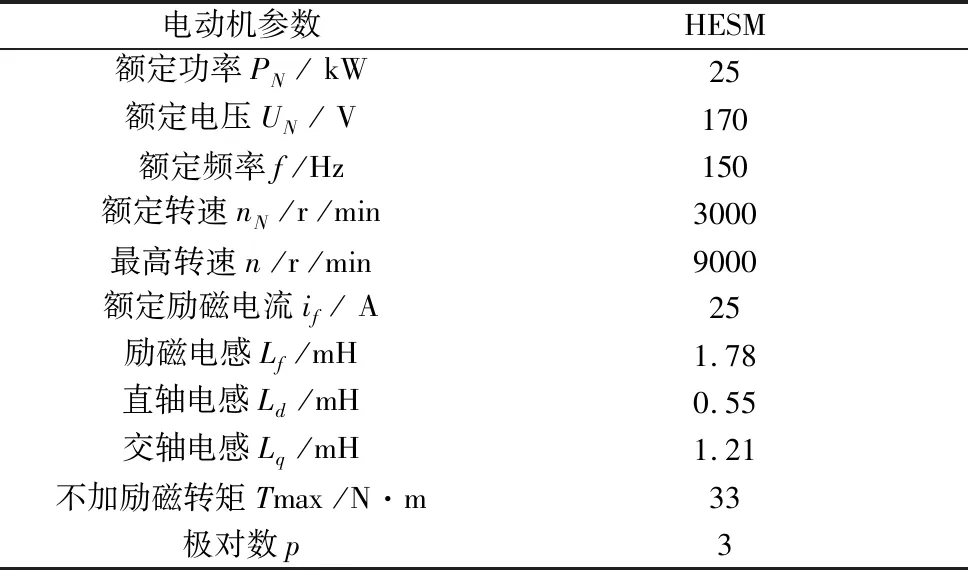
电动机参数HESM额定功率PN/ kW25额定电压UN/ V170额定频率f /Hz150额定转速nN/r /min3000最高转速n /r /min9000额定励磁电流if/ A25励磁电感Lf/mH1.78直轴电感Ld/mH0.55交轴电感Lq/mH1.21不加励磁转矩Tmax /N·m33极对数p3

2 HESM低速控制策略

对于直交轴电感不相等的HESM，在低速时适合采用最大转矩电流比控制[9]，其控制区域可以分为无电励磁区和增磁区。当负载转矩小于仅永磁励磁产生的电磁转矩时，则不加励磁电流，采用传统永磁同步电动机最大转矩电流比控制方法；当负载转矩超过仅永磁励磁产生的最大转矩时，则根据定子电流IS的大小对励磁电流进行调节，同时采用最大转矩电流比控制。

为了考虑磁路饱和的影响，采用有限元软件计算了不同定子电流情况下电磁转矩和励磁电流的关系曲线，如图2所示。

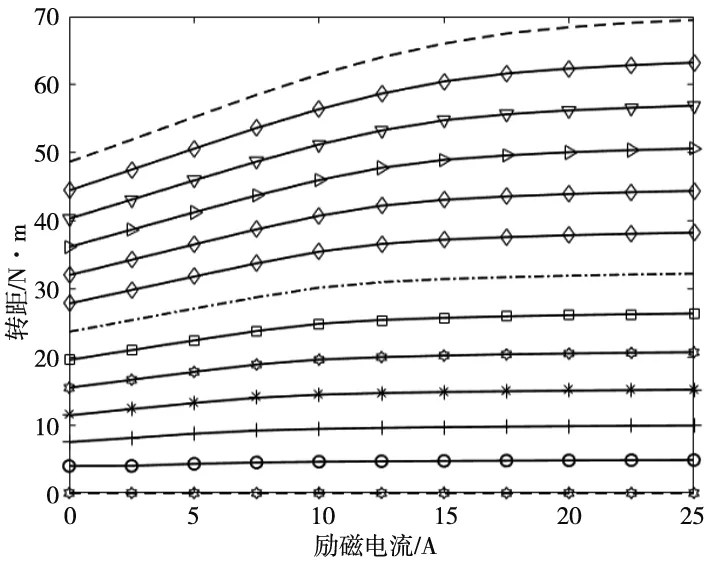
图2 不同定子电流情况下电磁转矩与励磁电流的关系

由图2可知，在磁路不饱和情况下，HESM电磁转矩随着励磁电流的增加基本成线性增长，当磁路逐渐饱和后，电磁转矩增长速率(斜率)随着励磁电流的增加逐渐变缓，最终保持不变。

根据图2所示结果，计算磁路不饱和时混合励磁同步电动机在不同定子电流情况下的电磁转矩与励磁电流之间的斜率K，如图3所示。

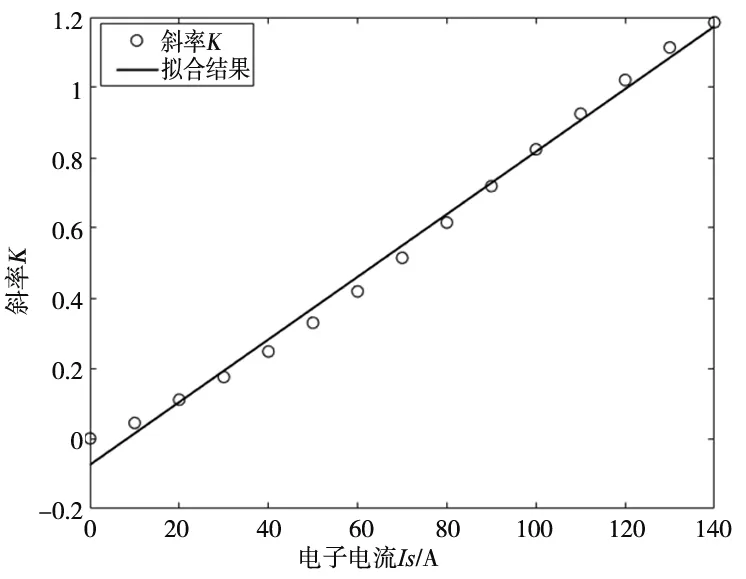
图3 拟合后的定子电流IS与斜率K变化关系

由图3可知，斜率K与定子电流IS之间也呈线性关系，可以表示为：

K=aIs+c

(1)

式中，a、c为系数。

当负载转矩TL超过仅永磁励磁产生的最大转矩Tmax时，根据定子电流IS对应的斜率K，得到需要施加的励磁电流为：

(2)

根据图2和图3所示数据，磁路进入饱和区时的励磁电流转折点约18.3A，超过转折点后，励磁电流则直接输入额定励磁电流ifN，可以用下式进行表示：

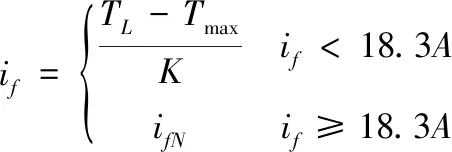
(3)

由图1所示混合励磁同步电动机的结构，根据恒功率变换原则，混合励磁同步电动机在dq旋转坐标系下的直交轴电流方程为

id=Iscosβ
iq=Issinβ

(4)

式中，β为定子磁链与转子励磁产生的气息磁场间的空间电角度。

定子电流方程为：

(5)

电磁转矩方程为：

Te=p(iqψd-idψq)=piq[ψpm+id(Ld-Lq)+Lfif]

(6)

式中，Ld、Lq为直交轴电感，Lf为励磁电感；id、iq、if分别为直轴电流、交轴电流和励磁电流；ψpm为永磁体产生的磁链，p为HESM的极对数，ωe为电角速度。

混合励磁同步电动机最大转矩电流比控制，电流矢量应满足的条件为：

(7)

(8)

根据式(4)～式(8)，可得最大转矩电流比控制时的直交轴电流如下：

(9)

(10)

根据式(3)、式(5)、式(9)、式(10)，可以实现混合励磁同步电动机低速情况下最大转矩电流比控制。

3 HESM高速控制策略

混合励磁同步电动机在达到额定转速后，继续扩速使得电枢绕组上的反电动势增大，导致定子电压超过变频器极限电压，因此混合励磁同步电动机高速运行时需要对其进行弱磁控制。

由式(11)可知，直轴电流id<0，此时直轴电流具有弱磁效应。随着电动机电磁转矩的增大，直轴电流id的绝对值随之增大，所以弱磁效应逐渐增强，导致弱磁基速nbase逐渐增加。通过有限元仿真软件计算了转矩与弱磁基速的关系曲线，如图4所示。

同时根据图4可知混合励磁同步电动机在不同转速下的带载能力，当采用Matlab/Simulink仿真时当没达到弱磁基速时，仍然采用最大转矩电流比控制。

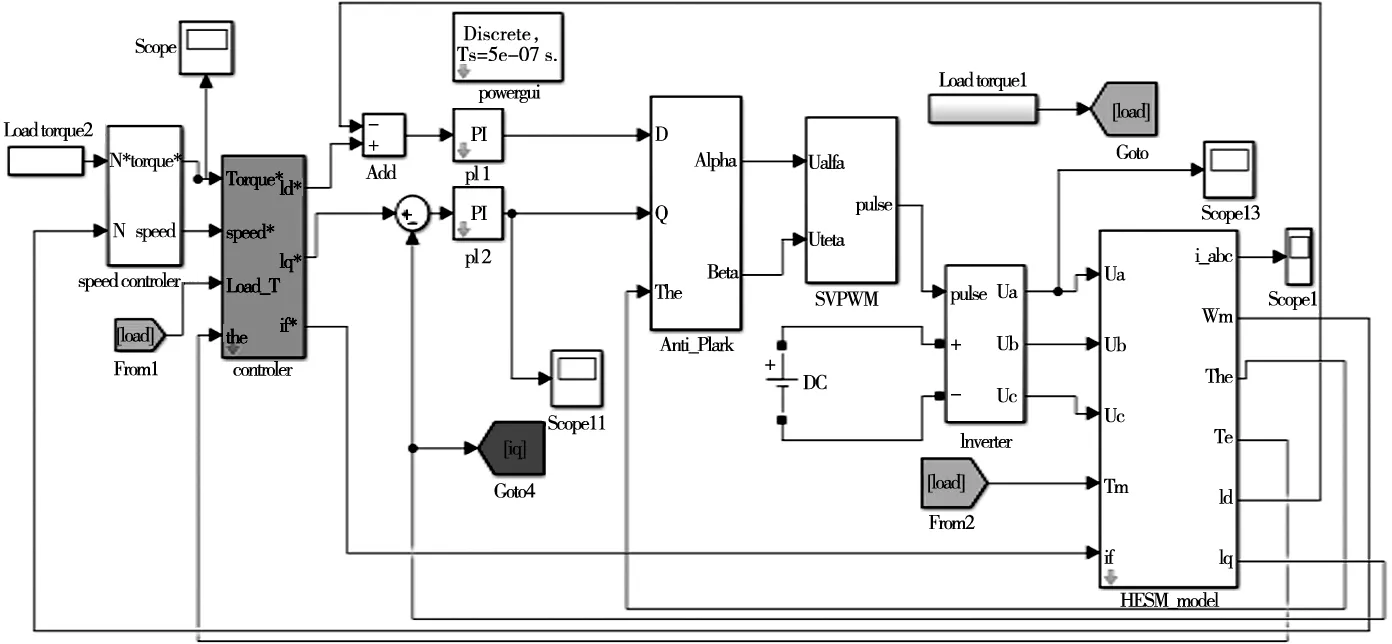
图6 控制系统仿真模型

当转速超过弱磁基速时，电动机进入弱磁状态，在保证电动机反电势不超过额定电压的情况下，计算了电动机转速与d轴磁链关系曲线，如图5所示。

由图5可知，转速与直轴磁链基本呈线性关系，因此可以通过线性插值查表得到不同转速情况下的直轴磁链ψd。

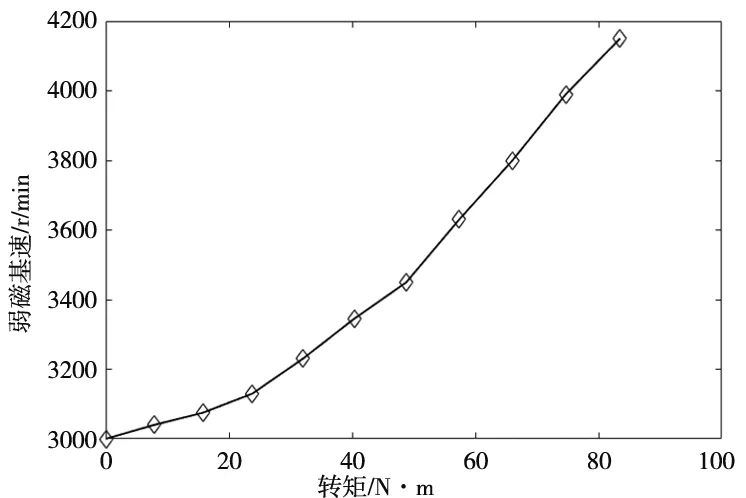
图4 转矩与弱磁基速nbase仿真曲线

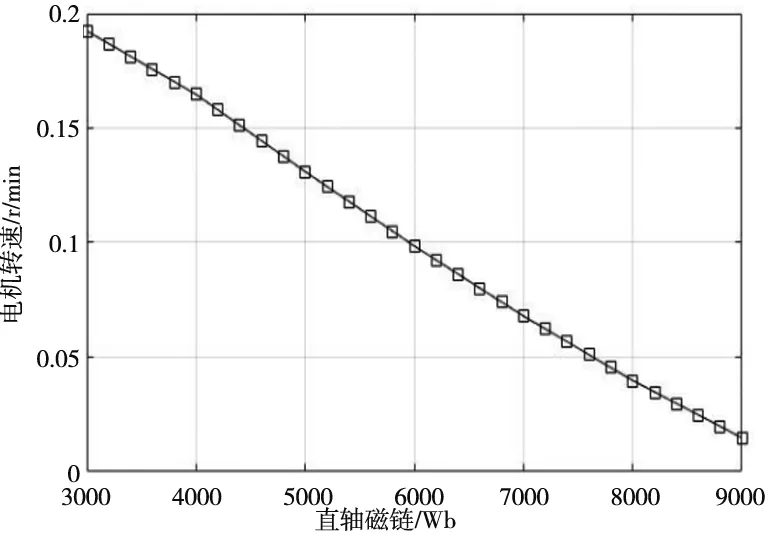
图5 转速与直轴磁链关系

为了提高混合励磁同步电动机高速弱磁运行的电磁功率和电磁转矩，可通过控制励磁电流以调节电动机的功率因数。当混合励磁同步电动机采用功率因数为1的弱磁控制策略时[10]，可采用以下控制算法。

电动机功率因数为1的条件为：

ψdid+ψqiq=0

(11)

直交轴磁链方程为：

ψd=Ldid+Lfif+ψpm

(12)

ψq=Lqiq

(13)

根据式(6)得到交轴参考电流为：

(14)

根据式(11)得到直轴参考电流为：

(15)

根据式(12)得到励磁电流为：

(16)

4 仿真分析

为了验证控制方法的正确性，采用MATLAB/Simulink建立了HESM控制系统的仿真模型，如图6所示。

基于前面提出的混合励磁同步电动机低速和高速运行时的控制策略，对混合励磁同步电动机的性能进行了仿真计算，其仿真结果如图7～图14所示。

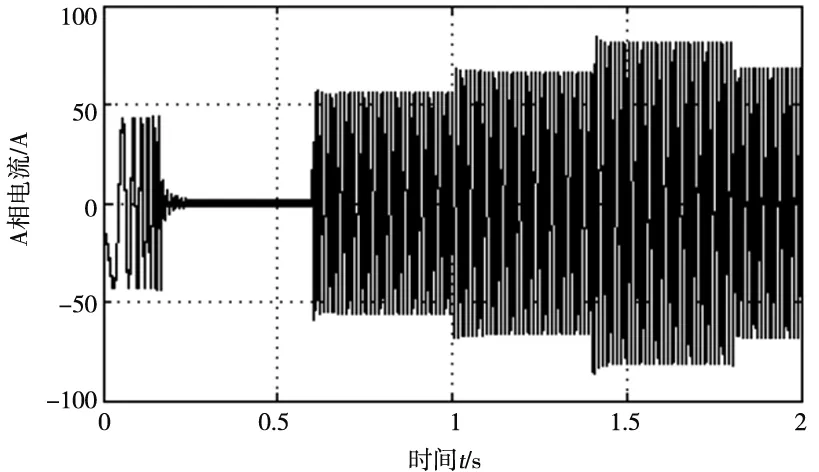
图7 低速运行时的定子A相电流

图8 低速运行时的转速曲线

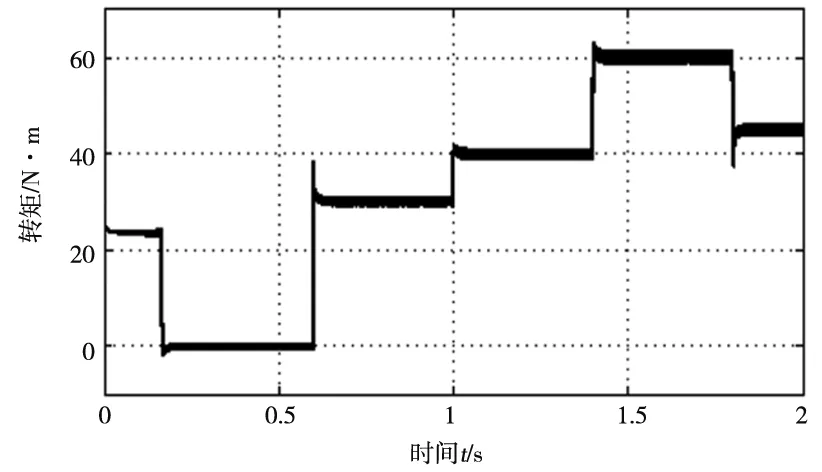
图9 低速运行时的转矩曲线

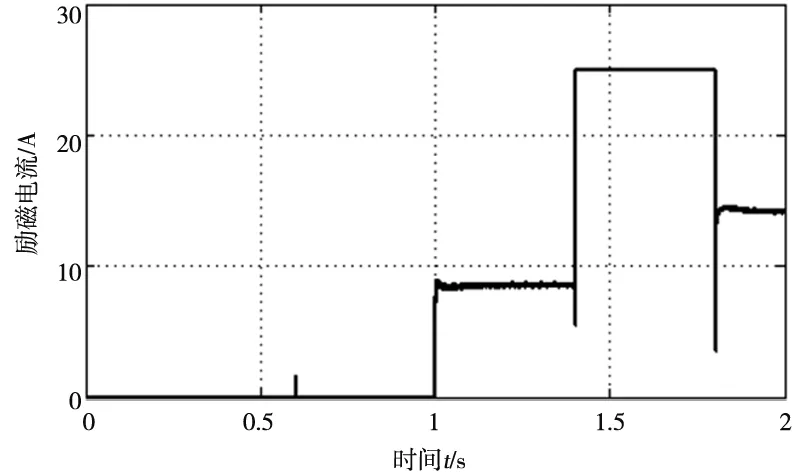
图10 低速运行时的励磁电流曲线

由图7～图10可知，当t=0.6s时，给电动机突加30N·m的负载，电动机转速几乎没有波动，励磁电流继续保持为0。在t=1s时将电动机的负载增加到40N·m，此时励磁电流从0增加到9.2A，在t=1.4s时突加负载到60N·m，此时励磁电流将超过其转折电流，则直接输入25A的额定励磁电流。当t=1.8s时，将负载减小为45N·m，励磁电流也随之减小，由此可以看出整个控制系统具有很好的动态响应。

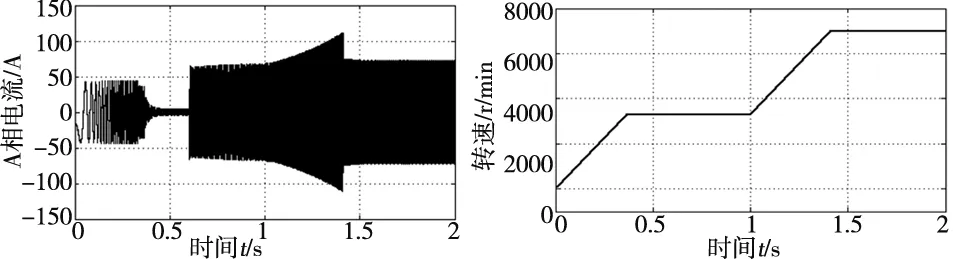
图11 高速运行时定子A相电流 图12 高速运行时的转速曲线

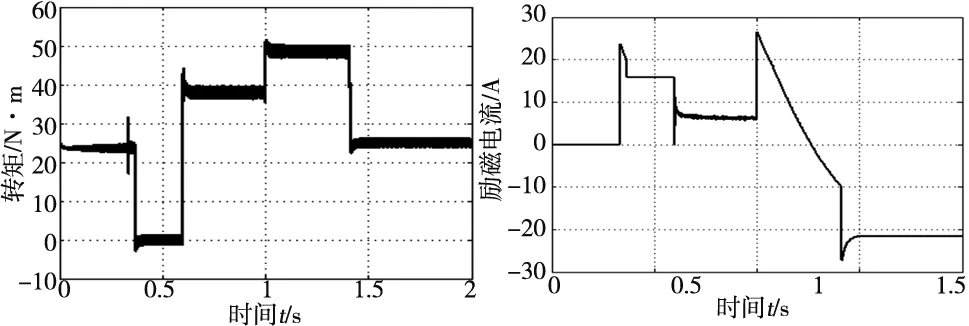
图13 高速运行时的转矩曲线 图14 高速运行时的励磁电流曲线

由图11～图14可知，电机运行分3个阶段。

(1)时间t从0s开始启动到0.33s时，由于此时转速超过电磁转矩对应的弱磁基速，励磁电流开始调节，电动机运行在功率因数为1的控制状态，电磁转矩出现波动，如图13所示，直到t=0.36s时HESM达到给定转速3300r/min，如图12所示，验证了功率因数为1的控制方法的有效性。

(2)t=0.6s时，给HESM施加38N·m的负载转矩，由图4可知，其对应的弱磁基速为3380r/min，大于电动机目前的转速，因此，HESM由功率因数为1的控制策略切换到最大转矩电流比控制策略，验证了该控制策略可以在低速和高速控制策略之间动态切换。

(3)t=1s时，给定负载转矩为25N·m，给定转速为7000r/min，超过该负载对应的弱磁基速，电动机又自动切换到功率因数为1的控制策略，励磁电流下降进行弱磁，电磁转矩上升提供加速度，在1.4s时电动机进入稳定运行状态。说明该控制策略具有很好的动态性能和抗扰动性，能满足电动机实际控制性能的需要。

5 结束语

本文针对一台混合磁极式混合励磁同步电动机，研究了其低速最大转矩电流比控制策略和高速功率因数为1控制策略，通过负载转矩的大小去判断弱磁基速，以弱磁基速做为高低速运行分界线进行控制。低速情况下通过定子电流动态调节励磁电流，实现HESM的最大转矩电流比控制；高速情况下通过功率因数为1的控制算法调节励磁电流，实现对HESM的功率因数为1的控制。搭建的MATLAB/Simulink仿真模型，验证了该控制策略可以实现HESM低速和高速运行状态的自动切换，并且具有很好的动态性能。