基于等误差阿基米德螺线法的涡旋型线的拟合算法研究*

刘 涛,李银萍

(兰州理工大学 机电工程学院，兰州 730050)

0 引言

涡旋型线是分析涡旋压缩机结构设计和加工的关键[1]，其决定了涡旋压缩机行程容积、载荷和泄露线长度等，从而最终影响压缩机的效率，故对涡旋型线的研究愈来愈成为近年来关注的焦点之一。

加工涡旋盘时，逼近涡旋型线的方式和拟合点的数量决定了涡旋齿涡旋型线的轮廓度[2]。对于组合涡旋型线这种既非直线又非圆弧的曲线，采用直线段或圆弧段去拟合时，过多的拟合点或者较大的拟合误差使得加工难度与工作量较大，加工较费时，导致加工效率不高或加工精度较低[3-4]。针对此问题，本文提出等误差阿基米德螺线逼近三段基圆渐开线组合型线，以期有效提高计算精度，减少节点数目，满足生产需要。

1 涡旋型线的数学模型

为了追求更大的压缩比，涡旋型线已从最初的单一的圆渐开线发展到现在的组合型线[5]。变截面涡旋盘母线可由三段基圆渐开线组合型线构成，在母线基础上可生成涡旋盘内外壁型线。涡旋盘型线方程为：

内壁第一段基圆渐开线：

(1)

内壁第二段基圆渐开线：

内壁第三段基圆渐开线：

外壁第一段基圆渐开线：

(4)

外壁第二段基圆渐开线：

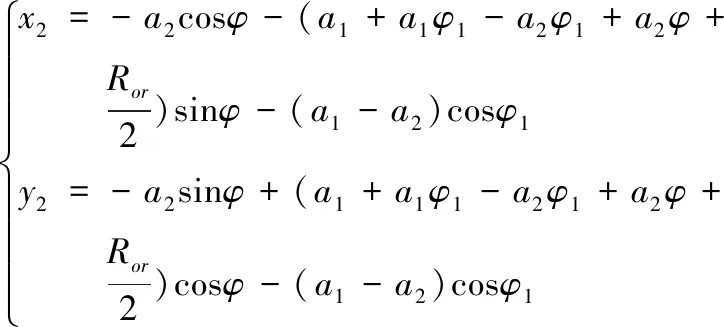
外壁第三段基圆渐开线：

式中，a1为第一段、第三段基圆渐开线的基圆半径；a2为第二段基圆渐开线的基圆半径；Ror为回转半径；φ为展角变量。取a1=2.890mm，a2=4.169mm，Ror=5.06mm，φ1=2π，φ2=4π，φ3=6π。根据以上解析式及给定的参数，利用MATLAB 软件，绘制出三段基圆渐开线涡旋型线图如图1所示。

图1 三段基圆渐开线涡旋型线图

2 等误差阿基米德螺线拟合原理与方法

2.1 拟合原理

在图2所示的坐标系中，给定某一段工件轮廓曲线，其极坐标方程表示为：ρ=I(θ)

(7)

为了加工出该曲线，本文拟采用阿基米德螺线[7]来逼近。取轮廓曲线上任一分段PiPi+1，过点P(θi,ri)，P(θi+1,ri+1)，作一条阿基米德螺线用来逼近渐开线，其方程为：

r=A(θ)=r0+Kθ

(8)

其中，K为阿基米德螺旋线系数，表示每旋转1°时极径的增加(或减小)量，可根据P(θi,ri)，P(θi+1,ri+1)两点计算得出：

(9)

以式(8)描述的阿基米德螺线来逼近渐开线时产生的极径之差即为逼近误差ε，则：

ε=|I(θ)-A(θ)|=|I(θ)-(r0+Kθ)|

(10)

图2 阿基米德螺线拟合原理图

2.2 拟合算法

利用阿基米德螺线逼近方程曲线时，拟合节点的数目和极坐标值主要决于曲线的特性和逼近线段的形状及逼近的允许误差，所选的逼近方法应该使得节点数少，计算过程简单，计算结果精确，因此采用等误差阿基米德螺线法逼近涡旋型线，即在每个分段中，令其拟合误差都相等。

采用等误差阿基米德螺线法逼近涡旋型线进行节点坐标的计算，关键在于坐标增量Δri与Δθi的计算。将曲线极径分成若干段，相邻两点P(θi,ri)，P(θi+1,ri+1)的极径相差△r，则：

(11)

其计算过程是，首先设定拟合误差等于允许误差[ε]，由P0点开始，根据式(11)利用MATLAB软件编程得到满足条件的坐标增量Δr0、Δθ0和P1点极坐标P1(θ1,r1)，再以P1点为新的插补点，以同样的方法确定坐标增量Δr1、Δθ1和下一个坐标点P2(θ2,r2)，重复以上计算过程，如此得到所有离散点的极坐标值，节点数目共计i个，将这些离散的点连接起来，即为拟合后的曲线。等误差阿基米德螺线拟合流程图如图3所示。

3 拟合三段基圆渐开线涡旋型线的实现

图3 等误差阿基米德螺线拟合算法流程图

取已给出的组合涡旋型线作为待拟合曲线，设定基于等误差阿基米德螺线拟合方法拟合的允许误差[ε]=0.001mm。涡旋型线上任意节点的极坐标Pi(θi,ri)可根据型线在直角坐标系下的方程计算得出：

(12)

由式(12)和涡旋型线方程可知，极角θ与极径r均与涡旋型线发生角φ存在关系，故只需确定涡旋型线相邻两节点差值Δφ，便可求得确定坐标增量Δri、Δθi和拟合节点坐标Pi(θi,ri)。其拟合节点部分计算结果如表1所示，涡旋型线拟合节点图如图4所示。

表1 等误差阿基米德螺线法拟合型线部分节点坐标及Δφ取值

图4 涡旋型线拟合节点图

为了深入分析本文提出的等误差阿基米德螺线逼近涡旋型线方法的特点，将其与传统的等间距阿基米德螺线逼近涡旋型线方法[8]进行对比。等间距阿基米德螺线拟合方法拟合曲线时要求允许误差[ε]≤0.001mm，由此采用等误差阿基米德螺线逼近涡旋型线方法拟合涡旋型线时可设定允许误差[ε]=0.001mm，即两种方法的初始拟合误差均为ε=0.001mm，以涡旋型线内圈第一段基圆渐开线的初始部分为例，分别用两种方法实现型线的拟合，其起始点坐标为(1.0809，6.1424)，如表2所示。利用MATLAB编程计算可得初始发生角差值Δφ0=0.76，从表2可以看出，在满足误差的前提下，采用等误差阿基米德螺线逼近涡旋型线方法相较于等间距阿基米德螺线逼近涡旋型线方法，Δφ的取值在不断变化，从而可以快速准确的确定最佳拟合节点，计算精度较高。再者，当Δφ越大，节点数目会随之减少。同理，用等误差阿基米德螺线方法拟合各段涡旋型线。表3为各段型线拟合节点数，采用等间距阿基米德拟合算法的节点共计327个，而等误差阿基米德拟合算法的节点为179个点，比等间距阿基米德拟合少43.5%，其中拟合第一段型线的节点数减少量尤为明显。由此可知，等误差阿基米德拟合方式在保证误差合理地范围内拟合节点数目更少，占用内从小，计算过程简单，可进一步的缩短加工程序，提高数控机床的加工效率。

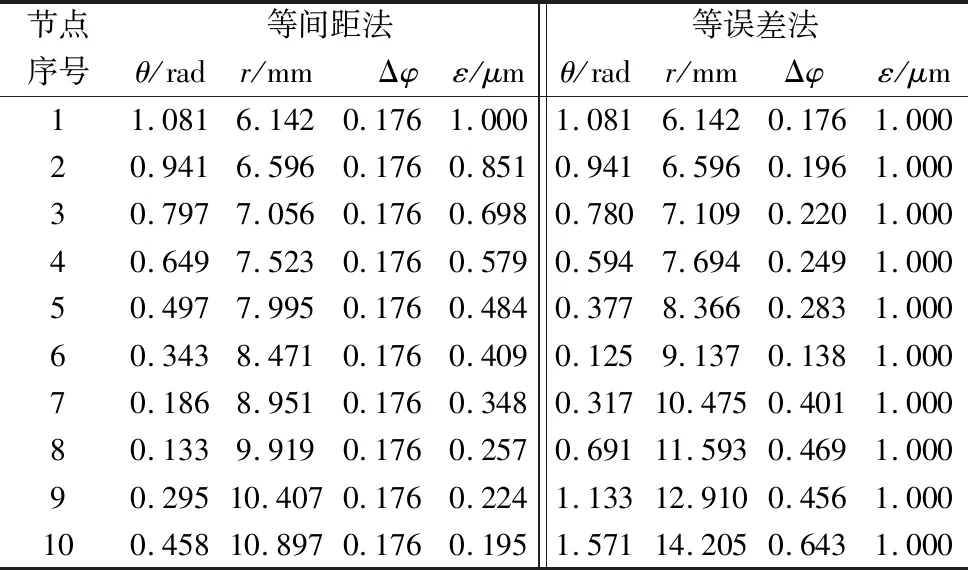
表2 阿基米德螺线拟合涡旋型线拟合方法对比

表3 涡旋型线各段型线拟合节点数目

4 结论

本文提出利用等误差阿基米德螺线法逼近三段基圆渐开线涡旋型线，并将其与等间距阿基米德螺线拟合方法进行了对比，发现等误差阿基米德螺线逼近加工曲线的计算精度较高，拟合节点数相对较少，可以满足数控系统高速实时性的要求，有效提高加工效率。