沙漏流动过程中重力变化现象
2019-07-01荆世宏李川南胡安平寻之朋
荆世宏,李川南,胡安平,寻之朋
(中国矿业大学 a.孙越崎学院;b.物理学院,江苏 徐州 221116)
沙漏作为时间的度量工具,在古时非常常用. 当沙漏中的沙子流动时,沙漏的重力会发生变化[1-3],如图1所示.

图1 沙漏中沙子流动现象
沙漏的重力发生变化,主要是内部沙粒运动使得施加在沙漏上的力发生变化所致[4-8]. 本文采用理论和实验相结合的方法,重点对沙漏中沙子流动导致沙漏重力变化的物理现象进行详细的研究.
1 理论分析
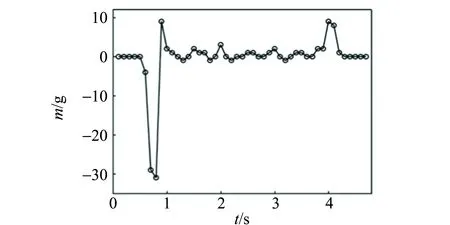
实验中发现沙漏重力变化如图2所示,沙漏重力变化过程大致可分为6个阶段,分别为初始阶段、重力减小阶段、重力回升阶段、重力稳定阶段、重力上升阶段和恢复原始重力阶段.
1.1 初始阶段
提取关键因素,建立如图3所示的简化模型. 在初始阶段,内部沙子处于静止状态,装置对底面的压力为定值,称为初始静压力. 此时,装置(包括沙子和沙漏)的重力即初始静压力为
(1)
其中M为容器质量,mi为沙漏中第i粒沙子的质量,n为沙粒总数量,g为万有引力常量.
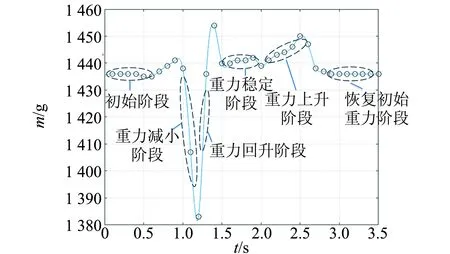
图2 沙漏重力变化实验曲线
对于沙子,写出质心方程
(2)
其中m为沙子总质量,yc为质心高度,yi为第i粒沙子高度.
实验中使用的沙粒很小,故可将(2)式推广为积分形式

(3)
式中ρ为沙子密度,S(y)为y高度时沙子整体的截面面积.
1.2 重力减小阶段

(4)
显然,此时重力小于静止时重力,表现为失重.
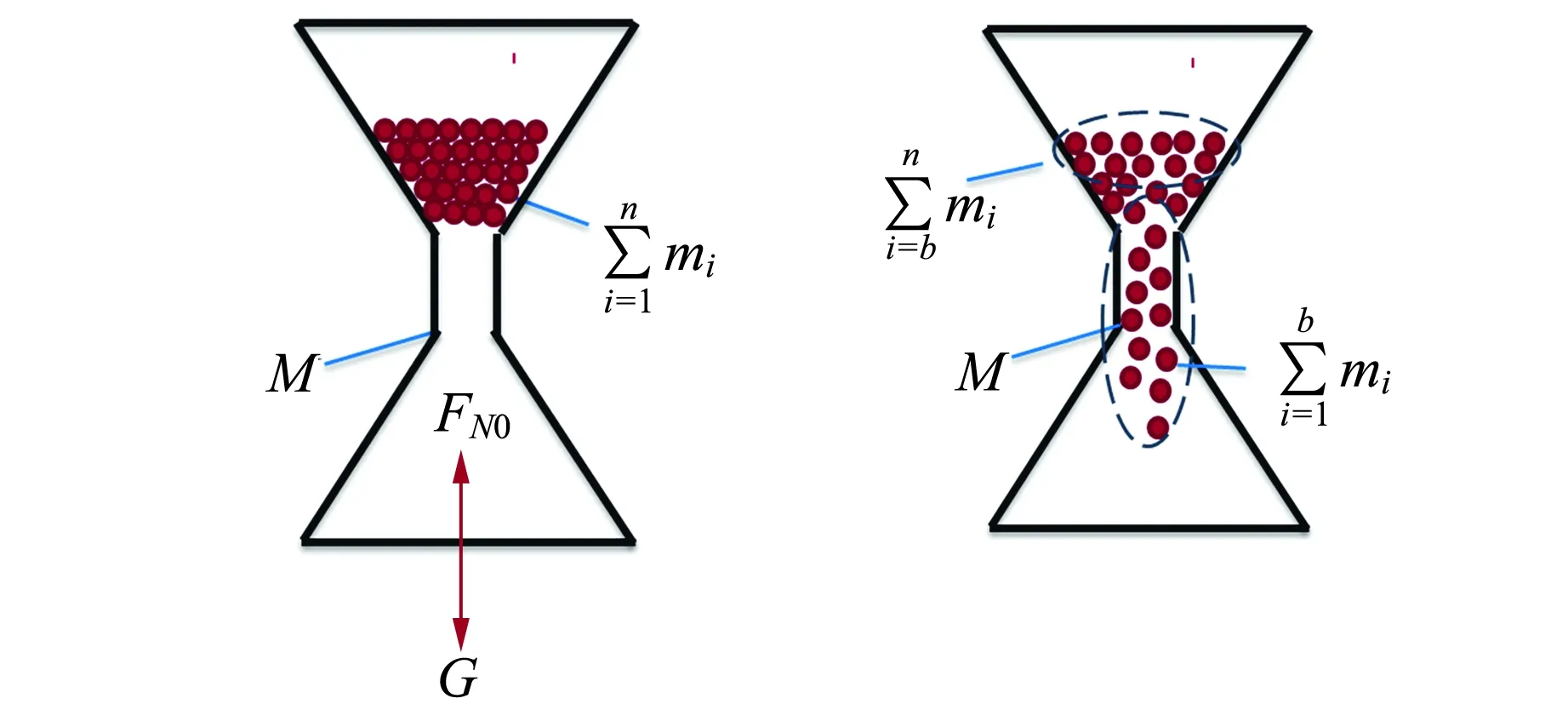
图3 初始阶段示意图 图4 重力减小阶段示意图
1.3 重力回升阶段
如图5所示. 此时,下落的沙子对沙漏底面产生冲击,由动量定理有
Δmv=FΔt,
(5)
即冲力的大小为
(6)
式中v为沙粒下落速度,Δm为刚好与沙漏底部接触的沙子质量,Δt为接触时间.
底面的压力为
(7)
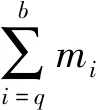
1.4 重力稳定阶段
如图6所示. 沙子稳定流动[9-12],此时的质心方程为

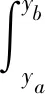
(8)
式中,λ为沙子的质量流密度,Sa(y)为沙漏上方沙子在y高度处的截面积,Sn(y)为沙漏下方沙子在y高度处的截面积.
沙流稳定流动时,式(8)第二项仅与沙子种类和装置结构有关,即
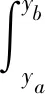
(9)
其中ξ(ρ)为取决于沙子种类的函数,ζ(h,σ)为取决于沙漏高度和孔径大小的函数.
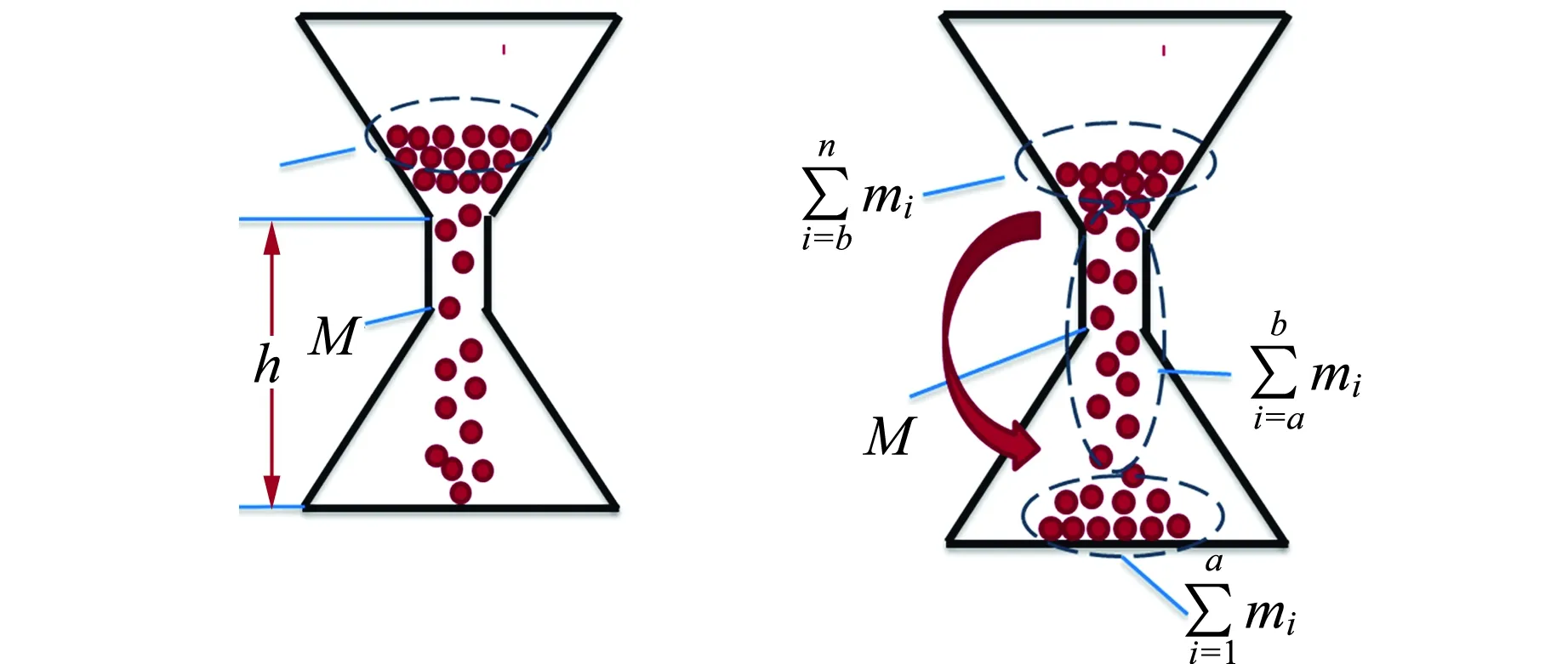
图5 重力回升阶段示意图 图6 重力稳定阶段示意图
将式(8)对时间求导,得
(10)
沙子稳定流动时,显然可以得到恒等关系,即
(11)
η为沙漏上方沙子总质量对时间的变化率. 因此式(10)可以写为
(12)
再对时间求导,得到质心的受力方程
(13)
由于是稳定流动,故式(13)第一项为零,将其代入式(11)得到
(14)
显然式(14)表征了沙子稳定流动时装置对底面的压力变化数值.
1.5 重力上升阶段
如图7所示. 在这一阶段,沙漏上部分的沙子全部漏完,下部分的沙子总重力不断增大,而滞留在空中的沙子还在持续下落,即沙子对底面的冲力持续存在,此时装置的总重力为
(15)
显然,此阶段重力数值将逐渐增大. 而当a→n即沙子几乎全部落完时, 重力大小应当大于静止状态时的压力,差值为F.
1.6 恢复初始重力阶段
如图8所示. 此时沙子全部落下,对底面冲量归零,沙子对装置的压力完全由重力提供,数值与静止初态压力相同,即
(16)
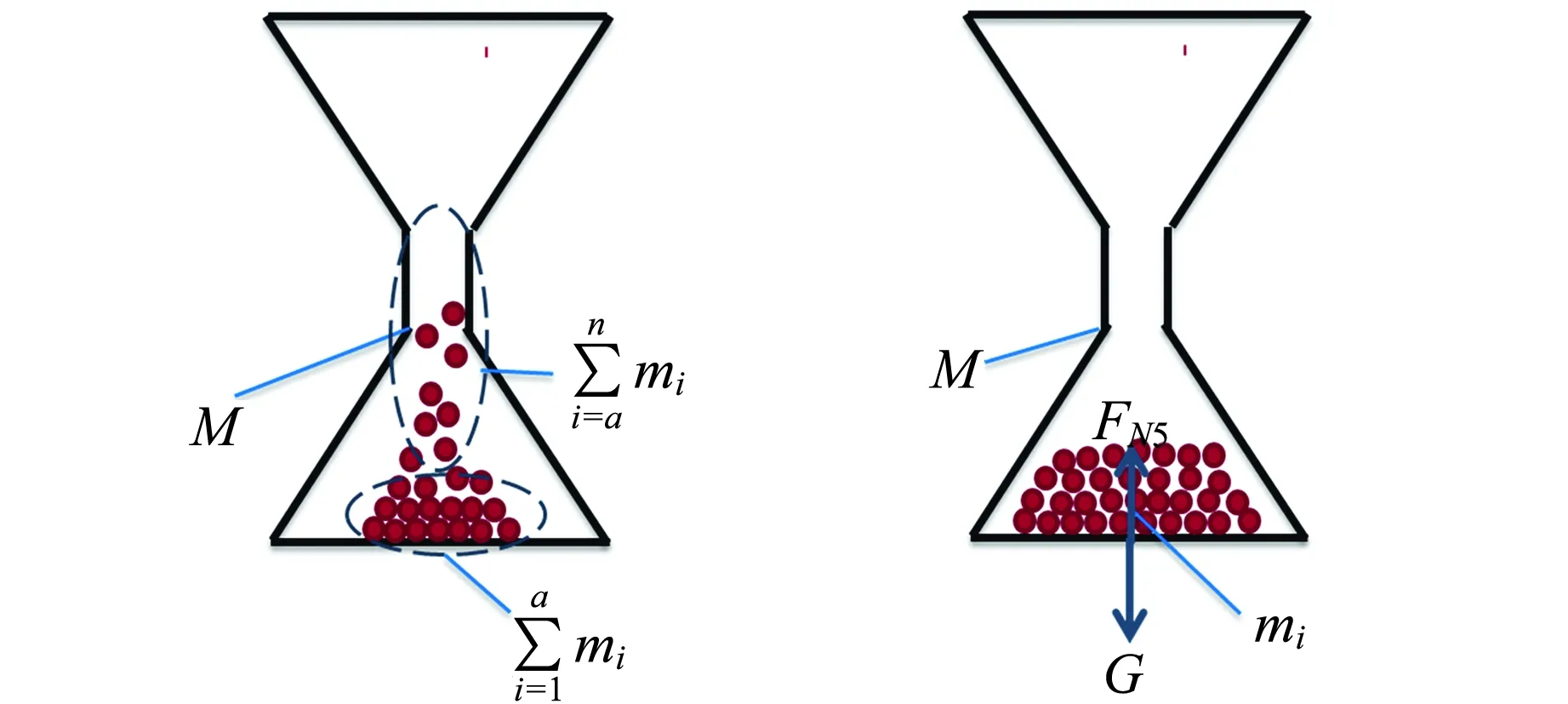
图7 重力上升阶段示意图 图8 恢复初始重力阶段示意图
值得注意的是,重力随时间变化的过程存在2个明显的峰:
第一个峰出现在重力回升阶段与重力稳定阶段之间. 重力回升阶段沙子开始冲击底面,装置总重力迅速回升,最初始时是沙子与沙漏底面的直接碰撞,两者之间无缓冲;而后续的沙子落在底面时,先前已经落下的沙子起到缓冲作用,因此后续的沙子冲击底面时,底面受到的冲力要小于最初始直接碰撞时的冲力,从而产生第一个重力变化峰.
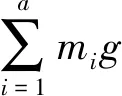
(17)
当滞留在空中的沙子全部落到沙漏底面,此时冲力F消失,装置总重力变为(16)式. 装置状态从重力上升阶段过渡到恢复初始重力阶段. 这个过程中,装置总重力经历了从(15)式到(17)式再到(16)式,从而产生第二个重力变化峰.
通过上述理论分析,可以做出如下理论预测:
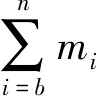
2) 空中滞留沙粒的质量与沙漏孔径和沙漏高度有关.
3) 沙漏粒径大小可决定重力稳定阶段沙粒流所产生冲击力的稳定程度.
2 实验研究
从沙漏孔径、沙子粒径、漏斗高度3方面对沙漏重力变化进行了实验研究. 所使用的测量装置及沙漏装置如图9~10所示. 实验过程用到了M400数据采集软件、高精度电子天平以及Arduino微控制器[13]. 实验过程中所采集到的数据为装置质量数据,由于实验过程中环境条件未发生变化,因此装置重力与质量为相互对应关系.

图9 测量装置

图10 实验装置
2.1 沙漏孔径的影响
图11所示为沙漏孔径为2.43 cm,2.76 cm,3.43 cm时,沙漏重力与时间的关系曲线. 设定初始时刻为零重力参考点,从图11中可知,3.43 cm孔径的沙漏在重力减小阶段达到极小值时,装置对外呈现的质量为-129 g,以g=9.8 N/kg,则装置重力为-1.264 N,而孔径为2.76 cm和2.43 cm时装置重力分别为0.608 N和0.412 N. 因此,沙漏孔径越大,沙漏在重力减小阶段所能达到的极小值越小;同样,在重力上升阶段,3.43 cm,2.76 cm和2.43 cm沙漏孔径在极大值处对外呈现的重力为0.823 N,0.294 N和0.225 N. 因此,沙漏在重力上升阶段所能达到的重力极大值越大;由图11可知,沙漏在重力稳定阶段的时间越短.

图11 改变沙漏孔径后沙漏质量与时间的关系图
2.2 沙子粒径
如图12所示. 分别为2~4目、4~8目、10~20目和40~80目沙粒从沙漏落下时,沙漏重力与时间的关系曲线. 从图12可知,沙子粒径越大,沙子对沙漏底部的冲击越离散,沙漏重力曲线的振荡现象越明显;粒径越小,沙子对沙漏底部的冲击越趋近连续,沙漏重力曲线越平滑.
(a)2~4目

(b)4~8目

(c)10~20目
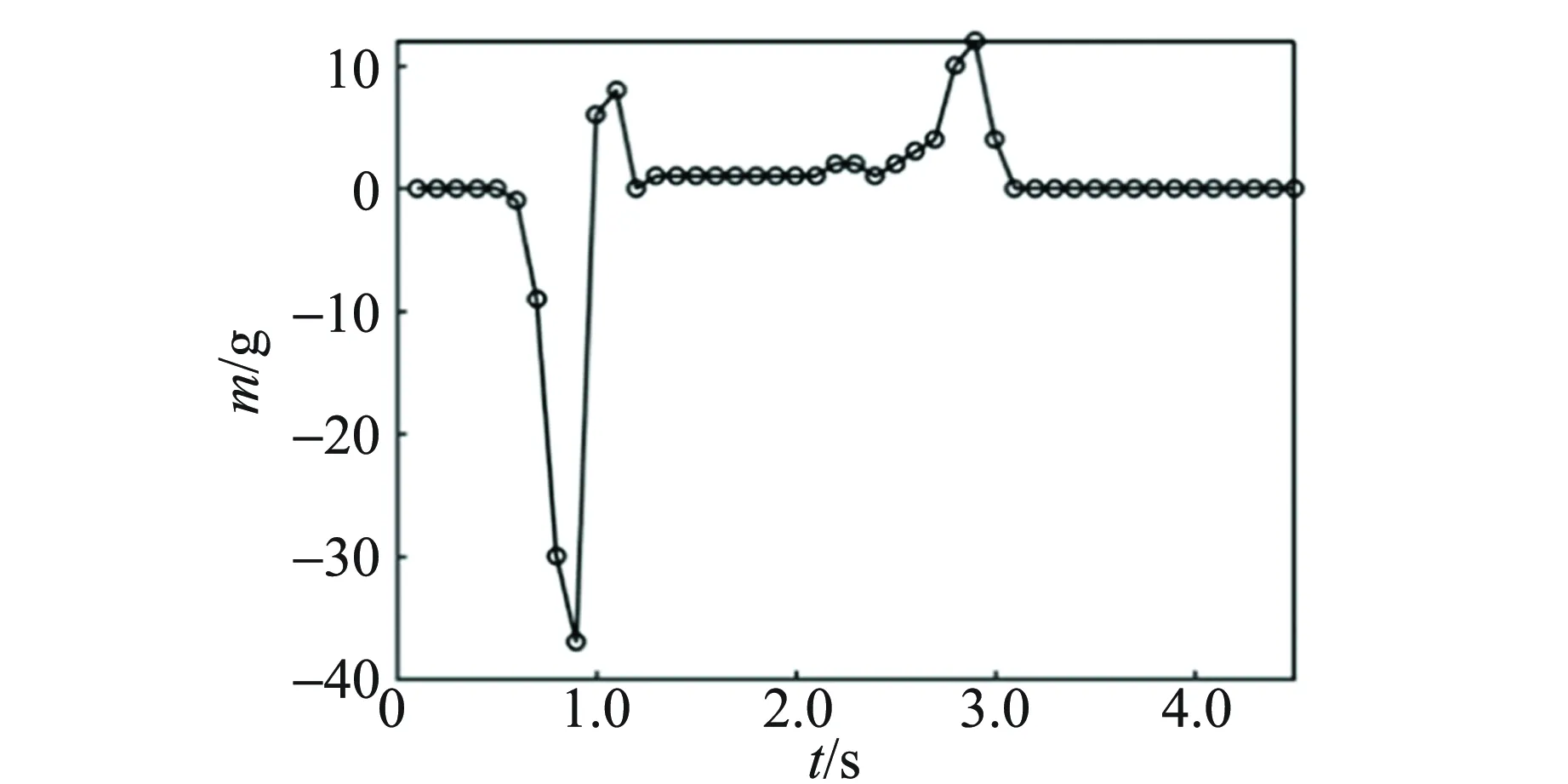
(d)40~80目图12 改变粒后沙漏质量与时间的关系图
2.3 漏斗高度
如图13~15所示,沙漏在不同高度处,下落距离与装置重力所达到的极值成线性关系. 分别对图14和图15中的沙漏最大重力、最小重力与下落高度的关系曲线进行拟合,得到沙漏最小重力Gmin(N)与下落高度h(m)的关系为
Gmin=-0.99h+14.30,
(18)
沙漏最大重力Gmax与下落高度h的关系为
Gmax=0.65h+14.52.
(19)
由以上分析可知,沙子下落高度越高,离开体系的沙子(未与沙漏直接接触的沙子)越多,沙漏所能达到的重力最小值越小,最大值越大.

图13 改变漏斗高度后沙漏质量与时间的关系图
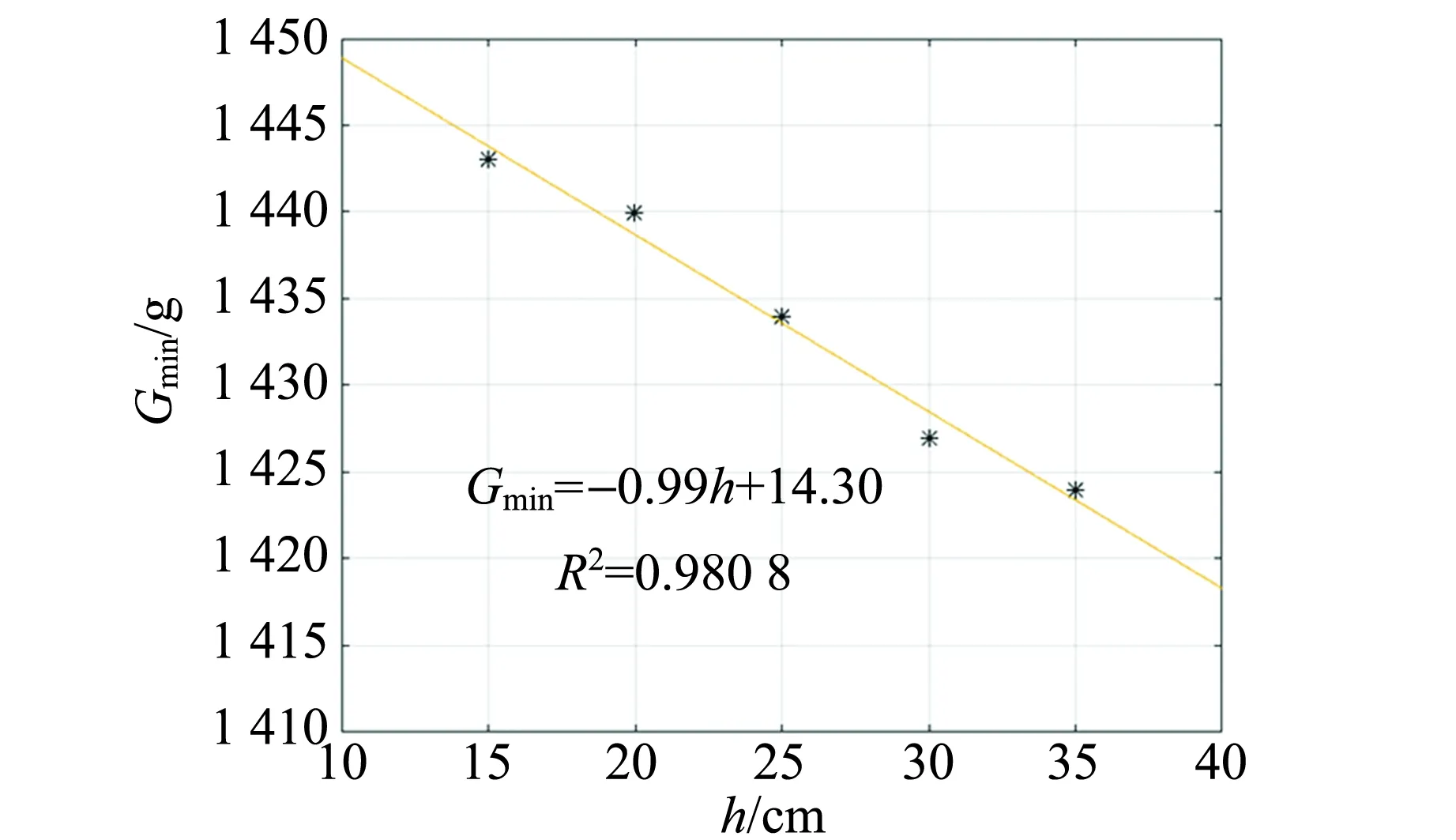
图14 沙漏最小重力与下落高度的关系
3 结 论
对沙漏中沙子流动导致沙漏重力变化进行了详细的研究. 依据实验曲线,将下落过程分成6个阶段并对每个阶段沙漏的重力进行了理论分析. 实验研究得出以下结论:
1)沙漏孔径越大,离开体系的沙子越多,沙漏所能达到的重力最小值越小,最大值越大,同时沙子漏下的速度越快.
2)沙子下落高度越高,离开体系的沙子越多,沙漏所能达到的重力最小值越小,最大值越大.
3)沙子粒径越大,沙子对沙漏底部的冲击越离散,沙漏重力曲线的振荡现象越明显;粒径越小,沙子对沙漏底部的冲击越趋近连续,沙漏重力曲线越平滑.
4)在考察的沙子粒径范围内,粒径越小,沙漏的流速越快.
