一道碰撞习题的独特解法与解法合理性的探究

史欣冉 俞逸骐 王乐

(合肥一六八中学 安徽 合肥 230601)

【题目】质量为m的钢板与直立轻弹簧的上端连接,弹簧下端固定在地上,平衡时,弹簧的压缩量为x0,如图1所示,一物块从钢板正上方距离为3x0的A处自由落下,打在钢板上并立刻与钢板一起向下运动,但不粘连,它们到达最低点后又向上运动,已知物块质量也为m时,它们恰能回到O点,若物块质量为2m,仍从A处自由落下,则物块与钢板回到O点时,还具有向上的速度,求物块向上运动到达最高点时距O点的距离．

图1 题图

1 常规解法

本题取自1997年高考全国卷物理第25题，在某高三一轮复习资料“考向卷”“考向22”第12题重现了此题[1]．从我校某宏志班(宏志班学生高考升学重点率在95%以上，211率在60%左右)学生答题情况来看，仅有少数学生能够一次性答对．其余的学生多数只能写出部分公式．但是，有一位学生给出了一种独特的解法，且最终的结果是正确的，此法思维独特，是碰运气做出来的还是有其深层次的合理性，经过师生的讨论，最终发现了其答案的偶然性，并进行了深入的分析，寻找到了新的异于其他论文的简单解法．

从问题的设计来看，这道题涉及到多个物体、多个过程，而且涉及到碰撞、弹簧以及能量等问题．运动过程比较复杂，对学生情景分析能力要求比较高．且只提了一问，梯度较大，无形中增加了解题的难度．考虑到物理计算题的常规做法，笔者认为这道习题可以增加两问．

第(1)问：第一次碰撞后瞬间钢板与物块的速度是多少？这样做的目的是让绝大多数学生都能够进入这道题．

第(2)问：第一次反弹至O点时，弹簧做了多少功？这两个设问，既降低了题目的难度，也给学生们提供了解题的思路．在如上3问的指引下，本题的常规解题思路如下.

(1)计算物块自由落体到钢板时的速度

得

物块与钢板碰撞过程

mv=2mv1

得

(2)此后，物块与钢板作为整体压缩弹簧并被反弹至O点，由动能定理求弹簧做功

得

(3)若物块质量为2m，则用同种方法可以求得碰后瞬间共同速度

之后经历了类似过程，由动能定理可以求得，物块与钢板再次到达O点时的动能

求得

注意两次的过程中，弹簧的形变量一样，因此做功大小相同．

最后，由机械能守恒定律

得

2 解法新探

(1)本文第一位作者认为，这道题能否将第二种情形中的物块质量分成两个m，考虑到下面的m与第一个情景完全相同，故若单独下落则能刚好反弹至O点，再考虑上面m的运动，将它看成是先做了一段位移为2x0的自由落体运动，获得一速度v，之后该速度瞬间反向并带着下面的m向上做竖直上抛运动，再求其上抛高度．运算如下.

自由落体

求得

速度反向并与下面的m共速向上

mv=2mv共

求得

竖直上抛

求得

这种解法十分简便，且结果正确．是凑巧相等还是有理论上的必然性，值得深入讨论．

从碰撞过程考虑，提出如下问题：一动碰一静的完全非弹性碰撞中，是否质量为2m的物体与质量为m的碰撞，可以将这种碰撞分成两个m分别与m碰撞，且这一过程中损失的能量与一次碰撞是相同的？从能量守恒的角度来看，由于最终具有共同速度，故能量损失肯定是一样的．但这种新解法分次碰撞，只考虑了一次碰撞，另一次碰撞则是在反弹回来之后人为地令其共速的行为．

如图2所示，若考虑为单次碰撞

λmv=(λ+1)mv共

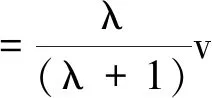
故损失能量

图2 将碰撞分为λ次

因此，该题中，如果是2m直接碰撞m的话，能量损失为

而新解法中只考虑了m与m的碰撞，考虑了两次.第一次，下落距离为3x0，这种碰撞的能量损失为

第二次，下落距离为2x0，能量损失值为

因此，这种新解法并不合理．

(2)本文第二位作者提供了新思路．考虑题目条件合理性：物块质量也为m时,它们恰能回到O点(题目为了能让高中生求解，因为高中不要求掌握弹性势能公式).

(1)

而第二次运动是类似的

(2)

而实际上，两式相减约去Ep即可求得v3的值，从而求解出上升高度．

当然，出题者可能是为了加入一些新意而选择给这种条件．但是，作为有确定劲度系数的理想弹簧，在确定了伸长量后，其Ep是一个定值，对于客观事实的存在给出条件求解的行为是否能经得住推敲？如若考生能够知道弹性势能的公式，或者是关系(前后两次初始Ep相等)，就有两种可能会绕过该条件，那么该条件确实有待斟酌．

(3)新解法提出

分离后运动的等效：实际上，我们在列第二次运动式子的时候是通过先求解v3来求解出上升高度h．但实际上我们知道，在O点时，我们将2m与m这两个物体独立开来看待,m由弹簧拉扯而做减速运动，2m与m不粘连而脱离弹簧．但是，实际上我们只是想表达m的运动对2m没有影响罢了．我们不难发现，在O点时，2m与m间是没有相互作用力的，那么m与弹簧是否黏连的意义不大，因为理想弹簧不过是储存能量的装置，所以当m与弹簧也能脱离时，m与2m应当都能上升到最大高度．提出这样的想法也是合理的,因为m与2m的加速度是一样的，完全可以看做一个整体．所以我们可以这样列式

(3)

结合上面的等效，我们可以进一步提出新的思路：

对于这样一个运动，第一次情形下与第二次情形下末状态的不同应当是来自于两者能量的差值

可以求得

而我们经过刚刚的讨论知道，2m到达最高点的高度与(2m+m)到达最高点的高度是相同的，所以

而我们知道，第一次恰好达到了O点，所以第二次高度应当比第一次高h，这即为本题的解．