两球同处先后落相碰反弹升多高

郑金

(凌源市职教中心 辽宁 朝阳 122500)

对有关两个小球在同一竖直线上以大小相等、方向相反的速度发生弹性碰撞而弹起的最大高度问题，若根据动量守恒定律和机械能守恒定律列方程解答则比较麻烦.而直接利用物理结论解答则很简捷.下面以一道高考题为例，对所得结果进行拓展，即通过改变两球的质量关系或碰撞点位置来求解最大高度的极值，由此归纳出结论并进行灵活应用.

1 结论推导

【原题】(2010年高考全国卷Ⅱ)小球A和B的质量分别为mA和mB，且mA>mB.在某高度处将A和B先后从静止释放.小球A与水平地面碰撞后向上弹回，在释放处下方与释放处距离为H的地方恰好与正在下落的小球B发生正碰.设所有碰撞都是弹性的，碰撞时间极短.求小球A和B碰撞后B上升的最大高度.

解析：如图1所示，两球碰撞前瞬时，球A的速度向上，B的速度向下.由于二者是在同一高度处释放，而所有碰撞是弹性的，则由机械能守恒定律可知，小球A与B碰撞前瞬时的速率相等，设为v0，则有

(1)

设球A与B碰撞后的速度分别为v1和v2，碰撞后球B的速度是向上的，以竖直向上为正方向，由动量守恒定律和机械能守恒定律分别有

mAv0-mBv0=mAv1+mBv2

(2)

(3)

联立式(2)、(3)得

(4)

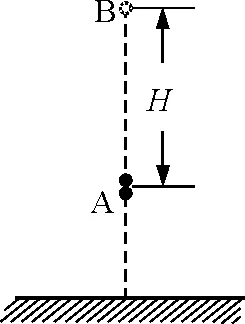
图1 两球相碰位置示意图

设球B从碰撞位置上升的最大高度为h，由运动学公式有

(5)

利用式(1)、(4)、(5)得

(6)

拓展:(1)如果碰撞后小球A的速度突然变为零，那么小球B上升的最大高度为多少？(2)两球的质量满足什么关系时，可使小球B上升的最大高度有极大值？(3)两球A和B在何处碰撞可使小球B上升的最大高度有极大值？

解析:(1)如果碰撞后小球A的速度突然变为零，那么球B的速度是向上的，对式(2)、(3)取v1=0，联立方程可得

v2=2v0

利用运动学公式有

可知小球B从碰撞位置上升的最大高度h=4H.

由式(2)可得质量大小关系为

mA=3mB

代入式(6)得

h=4H

由此可知，k越大，h就越大.当k→∞时，即当mA≫mB时，hmax≈9H.

(3)若两个小球不同时下落，则先后下落的时间间隔越短，碰撞点就越低，到释放点的距离H就越大，那么根据式(6)，球B上升的高度h就越大，因此当二者同时下落时，碰撞点最低，H值最大，所以球B弹起后上升的高度有极大值.

可见，直接利用式(6)解题可化繁为简.

结论:对于从水平地面上方同一位置先后自由下落的两个小球m1和m2(m1>m2)，若相碰位置到释放位置的高度为H，则上方小球从碰撞位置弹起的最大高度为

若下方小球与上方小球的质量之比越大，则上方小球弹起的高度就越大，当m1≫m2时，hmax≈9H；若两球同时下落，则上述h值最大.

2 结论应用

直接利用上述结论解答类似的问题比较简单，可避免根据动量守恒定律和机械能守恒定律列方程以及解方程组的麻烦.

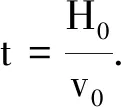
而

可得

设小球1和2碰撞前瞬时的速度分别为v1和v2，则有

v1=gtv2=v0-gt

即

由于两球相碰前的瞬时速度大小相等，方向相反，因此可等效为两个小球从同一高度处先后自由下落，质量较大的球与水平地面发生弹性碰撞后弹起再与质量较小的球发生弹性碰撞.由题意可知从释放点到碰撞点的高度为

设

则相碰后上方小球从碰撞点上升的最大高度

因此当m=9m1时，球1上升的高度最大，最大值为

对于该题，还有一种错误的解法，即认为碰撞后下方小球的速度立即为零时，把全部能量都给了上方小球，则上方小球被弹起的最大高度h=4H，可得二者的质量关系为m=3m1.

【例2】有两个钢球，密度相同，其中小球的半径为a，大球的半径为2a，小球置于大球顶上，开始时大球的球心到水平钢板平台的高度为h0，如图2所示.若两球从静止开始下落，假设两球心始终在同一竖直线上，而且所有的碰撞都是弹性的，求碰撞后小球将达到的最大高度(球心到钢板平台的距离).

图2 例2题图

解析:大球与钢板碰撞后反弹，再与小球相碰，由于二者一起下落，则相碰时的速度大小相等，那么由结论可知小球从碰撞位置上升的最大高度为

由公式m=ρV和球体积公式可知M=8m.两球同时下落，当大球接触钢板时两球发生弹性碰撞，可知上方小球自由下落的距离等于二者一起下落的距离，即H=h0-2a，因此小球从碰撞点上升的最大高度h可表示为

所以小球上升的最高点到钢板的距离

d=h+5a≈6.5h0-8a

点评:当两球上下叠放同时下落时，只有当下方球与钢板碰撞反弹时，两球才发生碰撞，由此来确定上方小球自由下落的距离，等于两球一起下落的距离，即为下方球面的最低点到钢板的距离，而不是球心到钢板的距离.虽然两球不在同一位置释放，但在一起下落，若不是在一起下落，则二者相碰时的速度大小不相等，那么结论不适用.

对于两道例题，尽管两球不在同一高度处自由下落，但仍可利用结论来解答.要注意结论的适用条件，包括3方面：

其一，两球正碰前的瞬时速率相等，这就要求半径忽略不计，且在同一位置释放，但不一定同时释放，若半径不能忽略，则须两球上下叠放同时释放，即二者一起下落；

其二，所有碰撞都是弹性的；

其三，位于上方小球的质量较小.

还要注意结论式中各距离的含义，其中H是指相碰位置到释放位置的距离，实际是上方小球自由下落的距离；而h是指上方小球竖直上抛运动的最大位移.该结论适宜解答选择题和填空题，而对于高考题中的论述计算题，要慎用结论，但可借助结论来检验常规解法所得结果是否正确.