余弦曲线轨道背景下小球运动加速度的变化

魏学锐

(佛山市南海区石门中学 广东 佛山 528200)

笔者在教学中，遇到一道值得深入思考的题．原题如下：

【题目】如图1所示，甲乙两光滑的小球原来在水平面以相等速度向右运动，现甲向右运动要通过一段坡路ABC，乙要经过一个坑DEF，若经ABC和DEF的路程相等，两球通过C或F到达右端水平面的速度相等，则( )

A.甲由A到C的时间比乙由D到F的短

B.甲由A到C的时间比乙由D到F的长

C.甲由A到C的过程中加速度先减小再增大

D.乙由D到F的过程中加速度先增大再减小

图1 题图

针对选项C，D，因为涉及到曲线运动，并且未告知曲线的方程，解答起来是相当困难的．下面我们详细对选项D进行分析，选项C用类似方法可以分析得出．

1 构建模型

由于曲线未知，我们根据形状，构建一个DEF轨道的轨迹方程为：y=Acosωx，建立坐标系如图2所示．

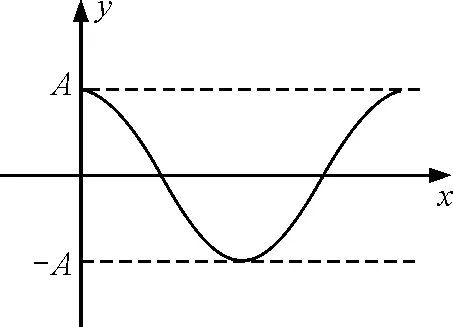
图2 曲线y=Acos ωx

有一质点以初速度v0从x=0处出发．此时我们要解决两个问题：

(1)该质点会不会脱离轨道运动？

(2)在不脱离轨道运动的情况下，加速度的变化是怎样的？

2 解决问题

2.1 讨论该质点会不会脱离轨道运动

假设在P点，该质点脱离轨道，则在P点只受重力作用．加速度分析如图3所示．

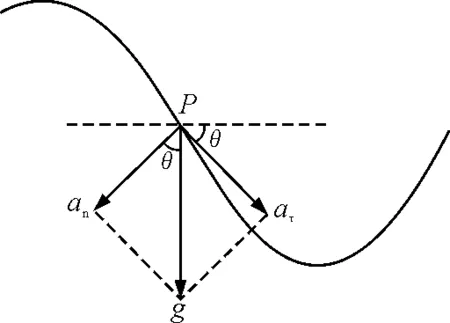
图3 P点加速度分析

易得

tanθ=|y′|=Aωsinωx

由三角函数关系可得

易得P点曲率半径为

从起点到P点，由动能定理有

在P点，由牛顿第二定律有

联立方程并整理得

(g+gA2ω2)=0

整理后得

若要让cosωx有解，则需满足

满足上式条件时，脱离位置由下解确定

特别地，当v0=0,ω=1时，Δ=-4g2A2<0，此时cosωx无解，则此时不会脱离轨道运动．

2.2 质点不脱离轨道运动情况讨论

如图4所示，一般曲线运动在自然坐标下的加速度由切向和法向两部分组成，即

a=aτ+an

考虑切向加速度，可以列出方程

mgsinθ=maτ

其中

故易得

考虑法向加速度，有

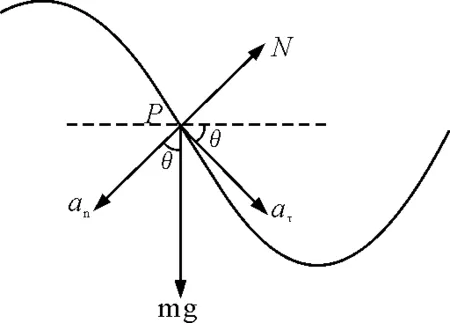
图4 P点受力及加速度图示

由2.1讨论，代入相关公式有

故该质点不脱离轨道运动情况下加速度大小为

即

使用软件作出a-x图，容易发现，a与ω和A关系很大．下面举两种情况看一下加速度变化的图像．

(1)A=1,ω=1,v0=0,g=9.8 m/s2．此时由图5可知，在x∈(0,π)内，加速度先增加，后减小；在x∈(π,2π)内，加速度先减小，后增加，再减小．最大值出现在x=π处．

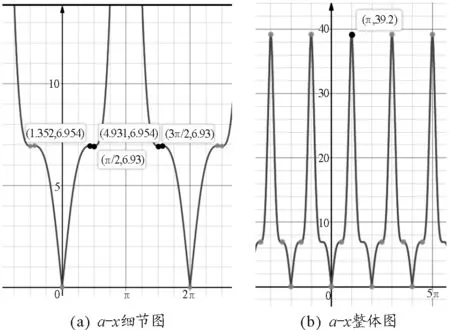
图5 情况(1)a-x图像

(2)A=1,ω=0.5,v0=0.1 m/s,g=9.8 m/s2．此时我们发现，在x∈(0,2π)内，加速度大小是单调递增的，如图6所示．

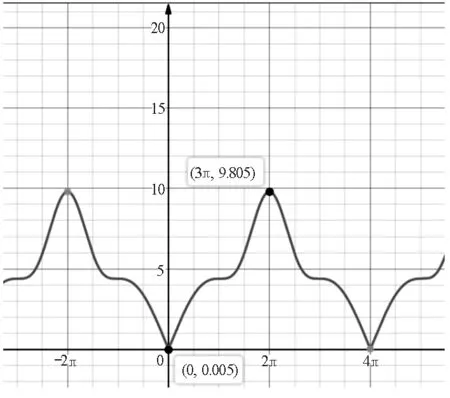
图6 情况(2)a-x图像

至此，我们发现加速度的变化在所建模型中是捉摸不定的，是会随着ω和A的变化而不同的．在给定特定参数的情况下，才能确定加速度的变化，自然也就证明了本文开始时提出的题目是有问题的．