基于磁场解析弹体飞行俯仰角的算法研究

于勇吉,林春生,翟国君

(1.海军工程大学兵器工程学院,湖北武汉430033；2.海军工程大学导航工程系,湖北武汉430031；3.海军海洋测绘研究所,天津300061)

0 引言

随着现代战争向信息化、智能化演变，常规弹药命中率较低的特点使之不再适合于复杂的作战环境使用[1]。目前弹体的飞行滚转角方式主要有：基于陀螺仪的测量方法，利用无陀螺的惯性组合测量，利用太阳方位角传感器进行测量，利用GPS导航器件测姿和运用地磁传感器的测量方式。在上述测量方式中，陀螺测姿的漂移误差会随着时间而产生积累，解算精度无法保证[2-5]。利用惯性组合和GPS导航器件受制于安装条件，太阳方位角传感器受气象条件影响较大。本文针对地磁传感器解算俯仰角的算法进行研究。利用构建的弹体姿态数学模型，推导出飞行俯仰角的解算方程，并对地磁场解算俯仰角的算法进行仿真试验和实物实验验证。

1 构建弹体姿态数学模型

建立弹体坐标系oxy和弹轴坐标系ox1y1z1[6-7]。模型中认为弹轴坐标系在初始发射时与弹体坐标系是重合的，弹轴坐标系的变化只与弹体俯仰和偏航的变化有关。模型主要研究弹体坐标系，其中ox轴为目标轴线方向，沿箭头方向为正，oz轴垂直地面指向下，oy轴与ox，oz轴构成右手坐标系。大地磁场方向和大小用B表示，其在oxy面内的投影与ox轴的夹角定义为磁方位角H，由ox轴偏向oy轴正方向取正。磁倾角I为地磁场与oxy的夹角，向下偏为正。弹体坐标系如图1所示。

图1 弹体坐标系示意图Fig.1 Schematic diagram of projectile’s coordinate system

弹体在短距离飞行过程中地磁场矢量基本保持不变，可将其视为常量。由图1可得地磁场在弹体坐标系oxyz上各轴的投影分量为[8]

当不考虑滚动时，假设弹体以一定的俯仰角P直线飞行时，地磁场在弹体坐标oxyz上各轴的投影分量可以表示为

若考虑弹体做小范围摇摆和俯仰随机运动，只需考虑俯仰角和磁航向角的时间变化，则有磁方位角和俯仰角的变化公式为[9]

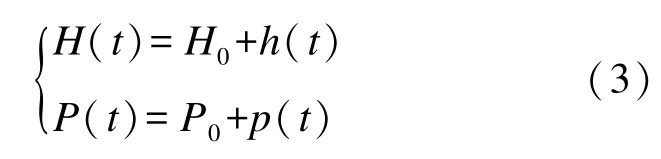
2 利用加速度计解算弹体俯仰角

通过加速度计测量弹体飞行俯仰角时，忽略加速度计离心力的影响，即将加速度计视为安装在弹体的旋转中心附近的理想状态，另外不考虑弹体章动角对于加速度计幅值的影响，其中g为重力加速度。弹体所受重力加速度在弹体端面上的投影如图2所示。

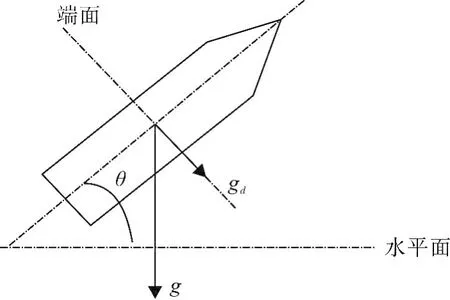
图2 重力加速度在弹体端面上的投影图Fig.2 Projection of gravity acceleration on end face of projectile

弹体在整个飞行过程中忽略风的阻力，且旋转过程视为匀速转动，不考虑弹体的切向加速度，那么加速度计的理论测量值为重力加速度与离心加速度[10]，由图中几何关系可得重力加速度g在弹体端面上的投影分量gd为

图3为弹体截面图，可求得g在弹体截面上的投影分量gd分别沿弹体径向和轴向上的分量为因此加速度计两轴的输出值为

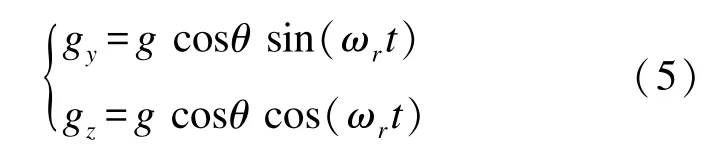
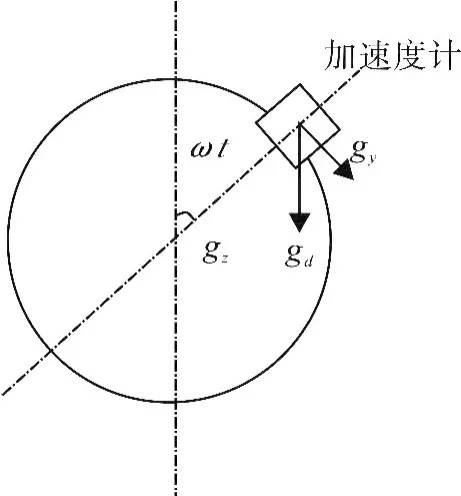
图3 弹体截面图Fig.3 Sectional view of projectile

因此采用加速度计解算出的俯仰角和滚转角为

但在实际测量中，由于加速度计受到离心加速度的影响，加速度计三轴的测量值会存在较大偏差，由此本文选用利用地磁进行弹体俯仰角的解析。

3 地磁传感器求解弹体俯仰角

对地理坐弹体相对地磁俯仰角Pc(t)做出分析。俯仰角Pc(t)为地磁场在xBOzB面内的投影与弹体OxB轴的夹角，规定向下为正。当弹体平行飞行时，俯仰角P=0，初始相对地磁俯仰角为[10]

由地磁投影关系可知，地磁场在补偿弹体滚转角之后，在OzB轴上的投影为Bz0(t)，则地磁场在坐标面xBOzB的投影为

则相对地磁俯仰角瞬态值为

由式(8)和式(10)，得到弹体瞬时俯仰角P(t)为

在短时间内平均俯仰角可近似计算为

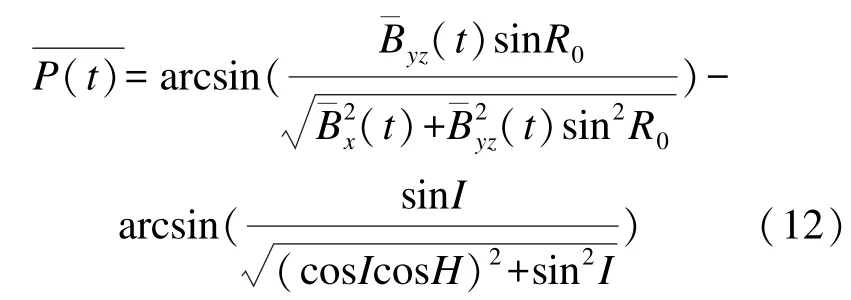
根据式(12)，在已知I和H的条件下，可以得到短时平均俯仰角

4 俯仰角测量试验

根据磁场解算俯仰角的方法分别进行算法仿真试验和单片机控制的地磁传感的实物实验。

4.1 算法仿真实验

为了验证算法的可行性，本文进行算法仿真。首先进行弹道仿真，给定初始条件：地磁场50 000 nT，磁倾角I=45°，方向斜向下，初始磁航向角H0=15°，弹体滚转角速率为200 r/s，俯仰姿角姿态维持在-10°(下压为正)，全程不考虑偏航角的变化，算法采样率为720 Hz，采样点为40 000个。为模拟真实的弹道参数，将仿真出来的磁场测量值添加上均值为0，方差为0.1 uT的高斯白噪声。得到的俯仰角度及其误差如图4-5所示。

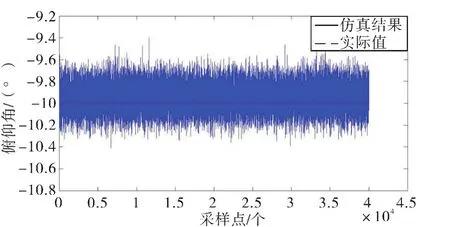
图4 俯仰角度示图(200 r/s)Fig.4 Schematic diagram of pitch angle(200 r/s)

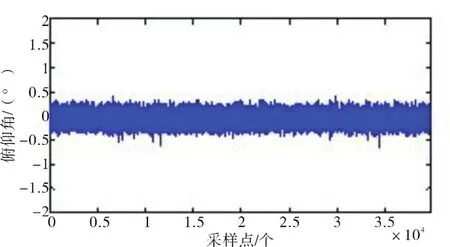
图5 俯仰角误差示图(200 r/s)Fig.5 Schematic diagram of pitch angle’s errors(200 r/s)

保持平飞状态，地磁场噪声信号均值为0，方差为0.1 uT，改变转速由200 r/s变为100 r/s，进行比对仿真试验，得到仿真结果如图6-7所示。

综上，俯仰角的解算误差在±0.4°以内，误差没有出现发散。

现对俯仰角发生变化的情况进行仿真分析。设定仿真所需要的初始条件不变，弹体自身旋转速度为200 r/s，设定俯仰角从-10°变化到30°。 得到图8-9所示结果。

图6 俯仰角度示图(100 r/s)Fig.6 Schematic diagram of pitch angle(100 r/s)

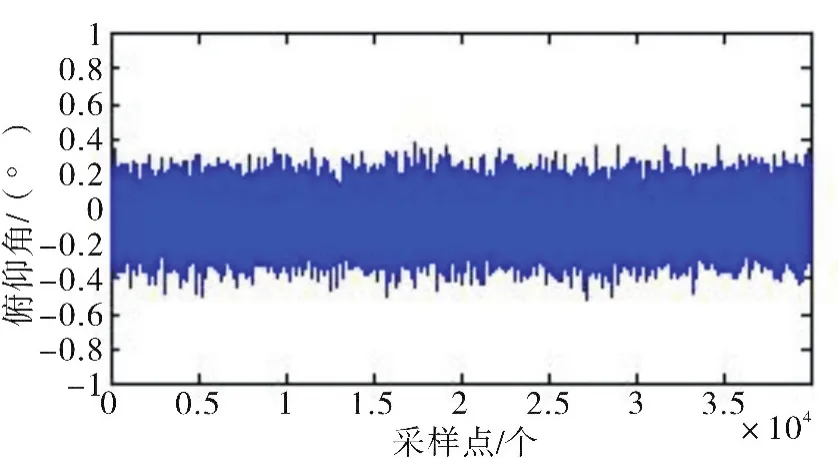
图7 俯仰角误差示图(100 r/s)Fig.7 Schematic diagram of pitch angle errors(100 r/s)

图8 俯仰角度示图Fig.8 Schematic diagram of pitch angle

图9 俯仰角误差示图Fig.9 Schematic diagram of pitch angle’s errors

从仿真实验结果可知：运用本算法解算出的俯仰角不随采样点的增多而产生误差积累。如图4-9所示，姿态角变化与理想值比对具有相同的变化规律。由此验证了算法的可行性。

4.2 地磁传感器解算滚转角实验

本实验选用的传感器是HoneyWell公司的HMC5883L型号磁传感器。选用的核心控制单元为STC15型单片机。测量系统组成的原理框图如图10所示。

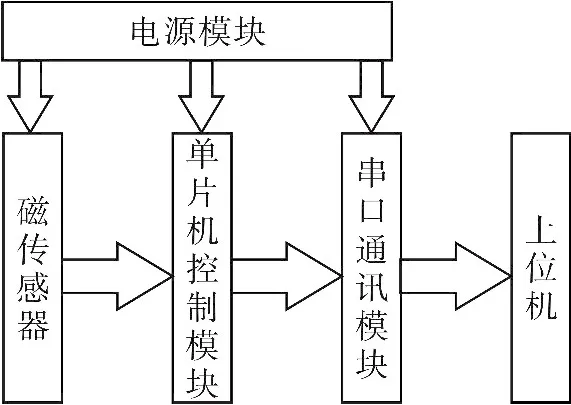
图10 系统硬件组成示意图Fig.10 Constitutional diagram of system hardware

在三轴实验转台上进行实验，设定转台内轴匀速旋转，角速度为0.872 5 rad/s，外框方位角保持为0°，进行弹体飞行俯仰角的模拟实验。设定转台中轴俯仰状态为正向5°(俯仰向下为正)，得到如图11和图12所示俯仰角及误差示图。

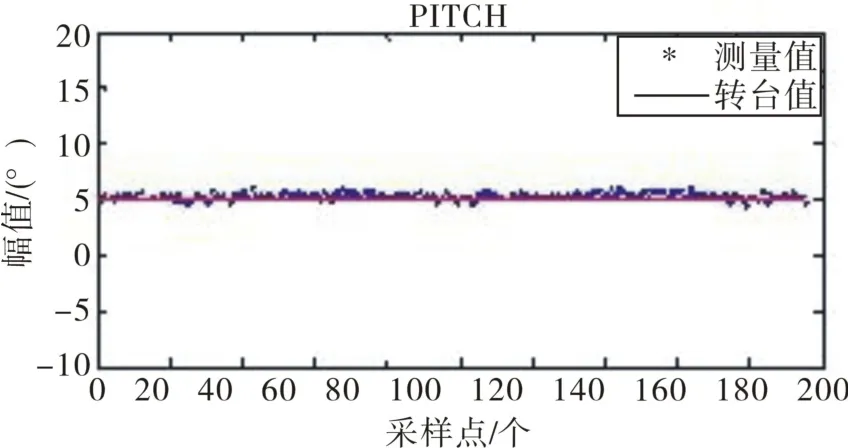
图11 俯仰角度示图Fig.11 Schematic diagram of pitch angle

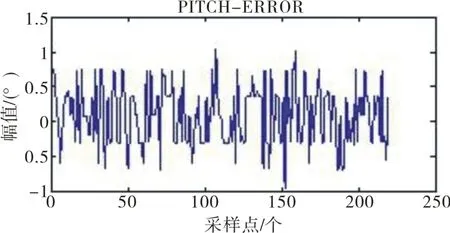
图12 俯仰角度误差示图Fig.12 Schematic diagram of pitch angle’s errors

由图11和图12可以看出，改变俯仰状态为负向后俯仰角误差仍然在±2°以内，属于合理的误差范围。

最后分析得出，实验结果与仿真结果相吻合，进一步验证了算法的正确性、合理性。同时随着俯仰状态改变，解算出来的俯仰角误差仍在合理范围内，表明其具有优越性与工程价值。

5 结束语

本文在建立的弹体姿态数学模型上，进行了地磁传感器解算俯仰角的算法研究。发现根据地磁解算弹体俯仰角，误差不会随着弹体转动而产生累积。最后，分别进行算法仿真和实物测量，结果表明该算法在弹体飞行俯仰角解算上的可行性，同时算法简单有效，在工程应用方面有广阔前景，与其他弹体俯仰角测量方法相比具有更高的实用价值。