含缺陷球柱组合壳极限承载能力分析

2019-06-28吴益辉万乐天

数字海洋与水下攻防 2019年2期

吴益辉,万乐天

(中国船舶重工集团有限公司第七一〇研究所,湖北宜昌443003)

0 引言

球柱组合壳结构是单壳体潜艇耐压船体结构的主要形式，其极限承载能力是衡量结构安全性的一个重要指标。单壳体潜艇具有超长舱和大分舱特点[1]，在静水压力作用下球柱组合壳结构的变形不再是单一的构件受载荷作用下的变形，而是会受到相邻结构构件变形的诱导，在连接处会产生应力集中现象，使结合处成为整个结构的薄弱环节，影响了整个结构的承载能力。国内外很多学者对柱壳或球壳的后屈曲变形和极限承载能力进行了相关研究，而对球柱组合壳的研究主要集中在力学性能的分析方法上，但少涉及到球柱组合壳及其试验相关方法。白雪飞等[2]设计制作了3个凹型加肋锥—柱/锥—环—柱结合壳系列精车模型，静水外压试验和计算结果表明，凹型加肋锥—环—柱结合壳能有效降低锥、柱壳结合部的应力峰值。郭日修等[3]通过分析加肋锥—环—柱结合壳中环壳块的应力分布特点，指出凹环壳块需局部加强的必要性，并提出了凹环壳块中部增设肋骨和凹环壳块适当加厚两种加强方式。ABS[4]及DNV[5]规范中给出了相对准确和可靠的水下航行器的相关设计方法和失效载荷；Radha和Rajagopalan[6]采用非线性有限元及蒙特卡洛法分析潜艇耐压壳体的承载可靠性，并利用Johnson-Ostenfeld弹塑性修正法及非线性有限元逼近法研究了加筋圆柱壳的弹塑性失稳，表明有限元法的精度高于理论计算。而关于初挠度的研究，往往通过导入其特征屈曲失稳模态波形实现，虽取得了较好的结果，但其失稳波形存在一定的假设，可能与实际情况不符，并且壳体结构在建造过程中其初挠度是很难用解析函数表示的[7]。

本文根据实测三维初挠度数据建立含缺陷的球柱组合壳有限元模型，计算了外部均匀压力作用下球柱组合壳的极限承载能力和变形，并与试验结果进行了对比分析，得到了组合壳体的变形与受力特性，为球柱组合壳体的优化设计提供了有效的依据。

1 球柱组合壳体结构力学性能

球柱组合壳结构在受均匀静水压力作用下的力学模型如图1所示。球冠结构边缘半径与轴线之间夹角为α，本文球柱组合壳体端面利用法兰固定，加压时力学模型可简化如此。

图1 球柱组合壳力学模型Fig.1 Mechanicalmodel of sphere-cylinder combined shell

2 球柱组合壳静水压力试验

球柱组合壳静水压力试验在模拟深海的压力罐内进行，3个球柱组合壳结构的焊接模型，分别命名为1#模型、2#模型和3#模型。这3个模型的圆柱壳结构尺度相同，球形壳壳板厚度与圆柱壳相同。1#、2#模型为半球壳结构，3#模型为球冠结构，球冠壳的圆弧角为120°，采用逐步加载法进行了强度试验和承载能力试验[8]。

分别利用回转平台、分度仪和高度尺等对3个球柱组合壳的壁厚及肋骨尺寸和肋骨间距进行了测量，其中壳体厚度及肋骨间距测量结果如表1-2所示。表1壳体厚度测量中涉及周向6个角度下的测量均值，取平均为最终壳体厚度；表2中li(i=1，2，3，4，5)表示肋骨离球柱组合壳连接处及相邻肋骨间的距离，其中2#模型有4根环肋。

表1 模型壳体厚度测量均值Table 1 Averagemeasurement values of models’hull thickness

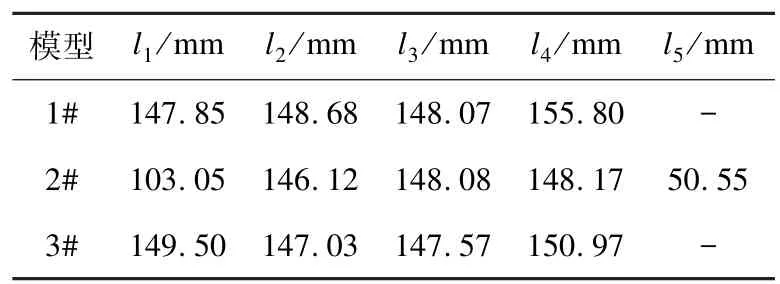
表2 模型肋距测量均值Table 2 Averagemeasurement values ofmodels’frame space

3 非线性有限元分析

3.1 模型建立

根据模型结构实测参数建立了相应含缺陷几何模型，壳体厚度及环肋加强筋由测量均值给出，组合壳半径R=155mm，肋骨截面为矩形且腹板长为l=10 mm，法兰半径r=195 mm，法兰板厚t=5.2 mm。球柱组合壳结构焊接模型材料弹性模量E=1.97×105MPa，泊松比μ=0.3，屈服极限σs=418 MPa。

3.2 数值仿真结果

试验及有限元结果见图2，由变形形状及应力集中区分布情况来看，两者符合的很好。1#模型最大变形发生在球壳与柱壳连接处靠近第一个环肋处；2#模型最大变形发生在柱壳第二与第三环肋中间处；3#模型最大变形则发生在第一与第二环肋中间处；变形区域平均 Mises应力分别达到539.5 MPa、476.9 MPa、442.7 MPa，可见，在外部均布水压作用下，组合壳结构均失稳破坏。

图2 变形及Mises应力分布Fig.2 Deformations and Mises stress distributions

试验中3个模型均发生总体失稳破坏，且失稳的部分为环肋圆柱壳部分。最终测得1#、2#、3#试验模型破坏崩溃压力分别为2.2 MPa、2.4 MPa、2.3 MPa，而有限元结果为 2.5 MPa、2.8 MPa、2.4 MPa。可见，组合壳2#模型有着较高的承载能力，与1#模型相比，靠近球柱连接处的环肋提高了结构的整体稳定性，其应力集中区较小；而3#模型与1#模型的抗压能力相当，其球冠结构使得变形区域下移，在连接处较大的结构不连续性使其产生了比1#模型更大的塑性应变；3个模型球壳部分应力分布较为均匀。

4 对比分析研究

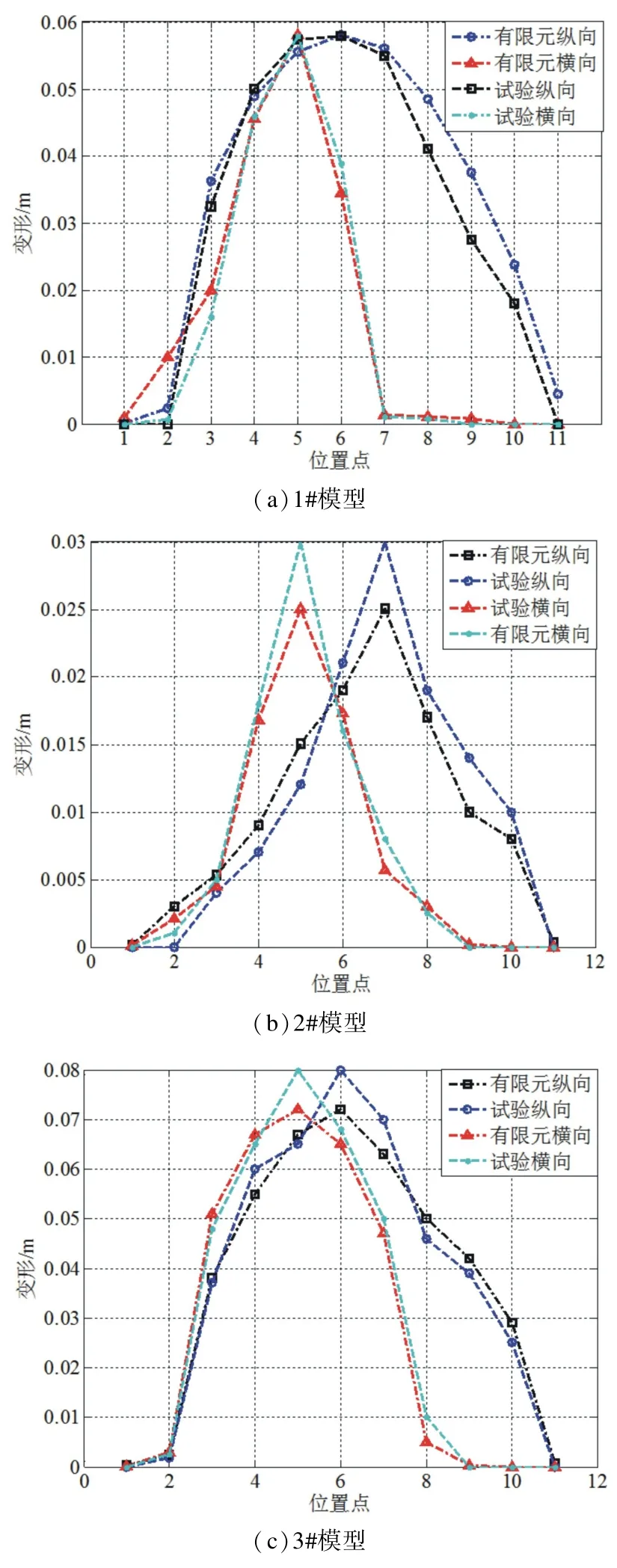
图3 有限元与试验变形对比Fig.3 Results comparison of finite element and experiment deformation

1#与2#球柱组合壳体极限承载能力分别为554.9 kn、551.2 kn，观察结构达到极限强度之后的后极限强度行为变化过程可以发现，2#模型的承载能力变化较1#模型缓慢，且具有较高的剩余强度，可见在连接处的加强筋对于球柱组合壳的后极限强度行为影响较大。3#模型承载能力变化与1#模型相当，但是最大抵抗反力相比1#模型较小，仅为539.8 kn，可见球冠结构的不连续性减弱了结构的极限强度。

输出和测量了纵向沿半壳体经线分别于球壳顶部、中部、球柱壳连接处及柱壳肋骨及肋骨中间11个位置点的轴向变形，横向对称沿半壳体纬线方向的9个位置点的轴向变形，均以最大变形点为基准点，且变形方向均为沿壳体半径方向。非线性有限元与实验结果如图3所示。由图3可知，1#与3#模型纵横向变形较2#模型平缓，2#模型由小变形到极限变形发展速度很快。1#与3#球柱组合壳连接处的3号位置点变形量较大，而2#球柱组合壳3号位置点变形量较小，说明靠近连接处的柱壳环肋加强在很大程度上影响了连接处的变形与应力分布。

表3为球柱组合壳最大变形数值模拟与试验结果对比，其误差分别为0.35%、19.61%、9.75%。2#模型较其他2个模型的误差偏大，可能是由于测量误差和有限元处理大变形时迭代路径的影响，但总体上可以看出非线性有限元结果与实验误差在工程结构物计算的可接受范围内，较为准确地反映了结构的实际变形。