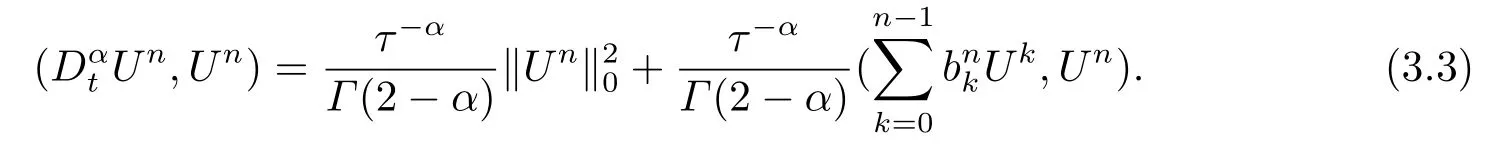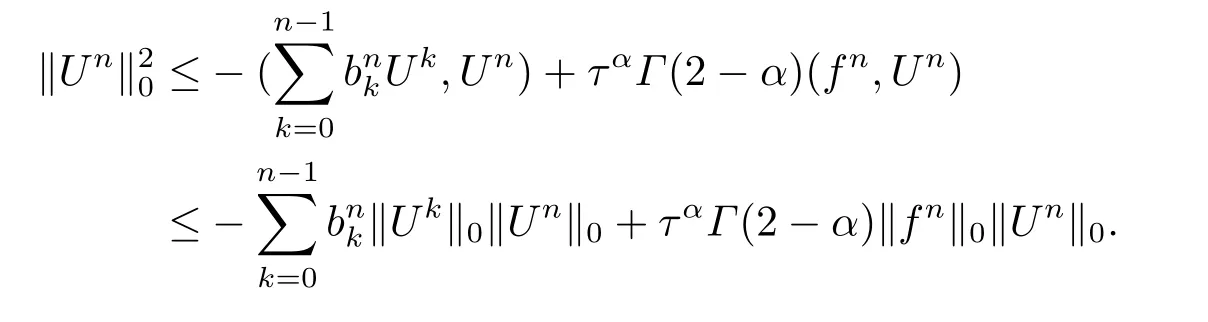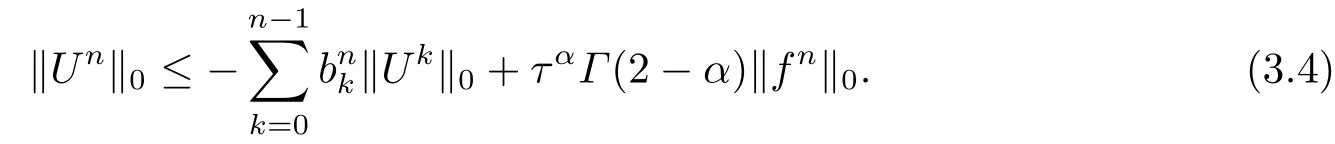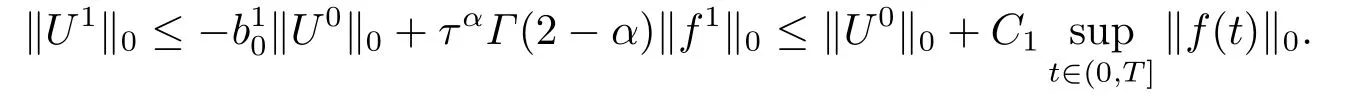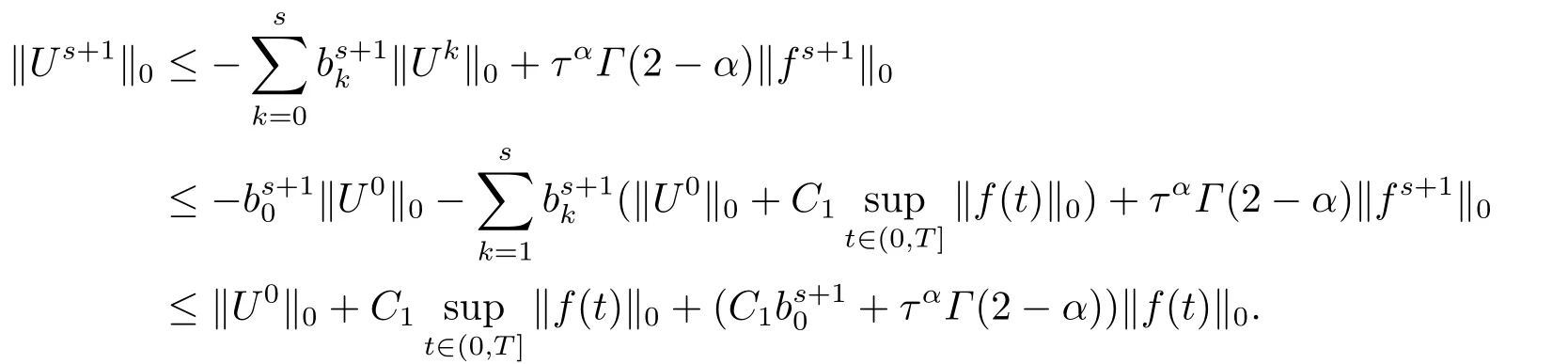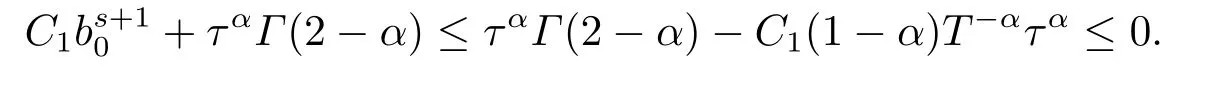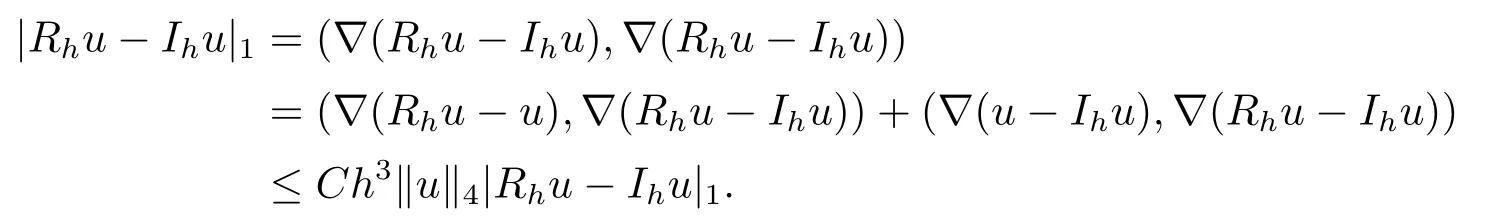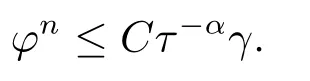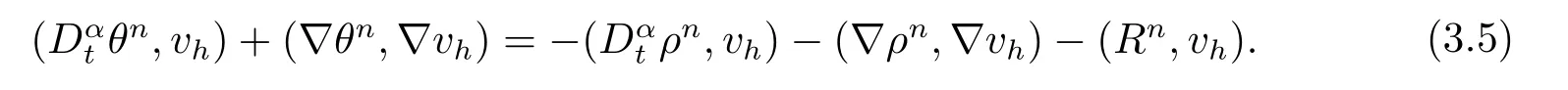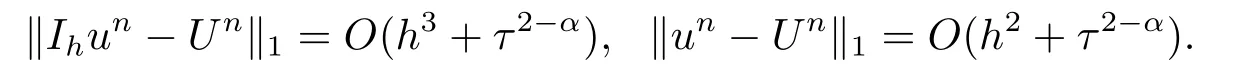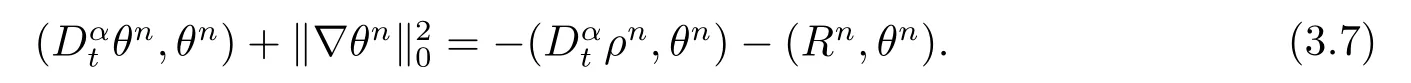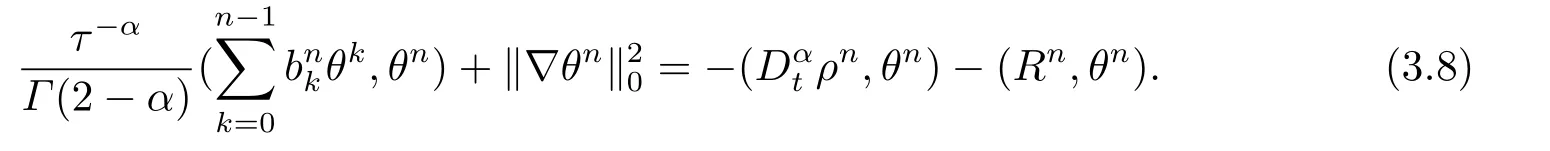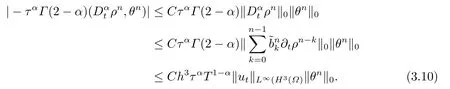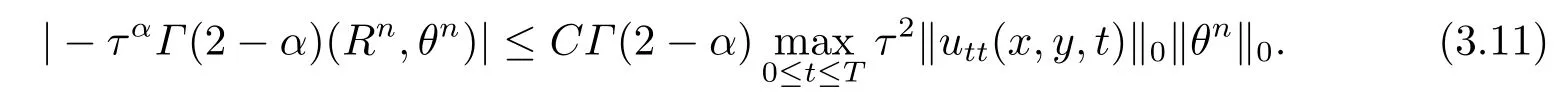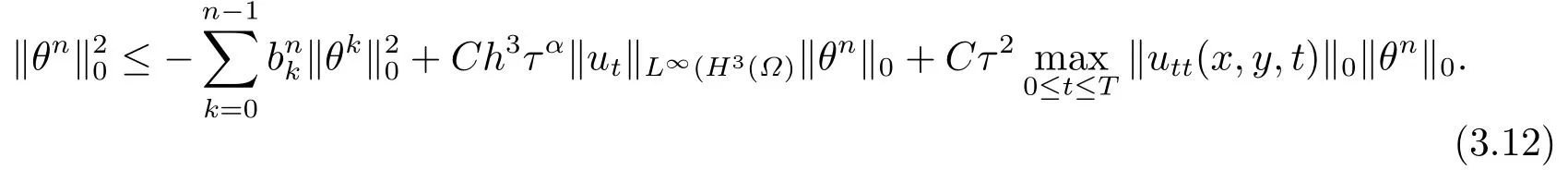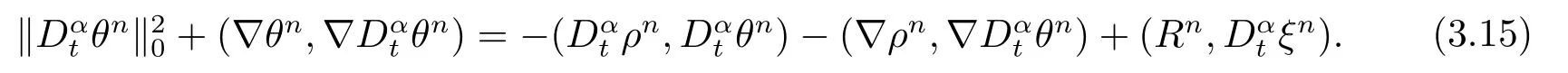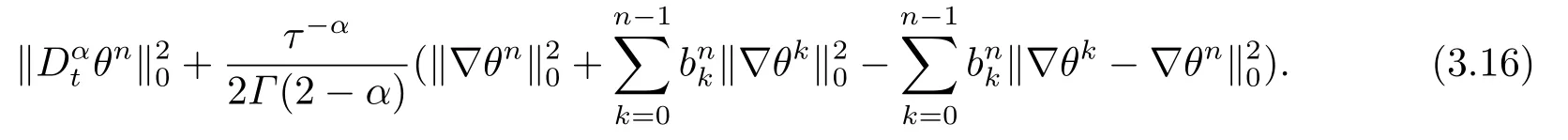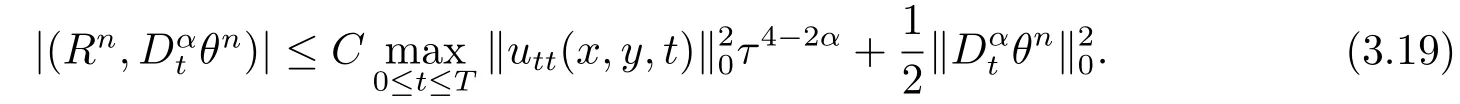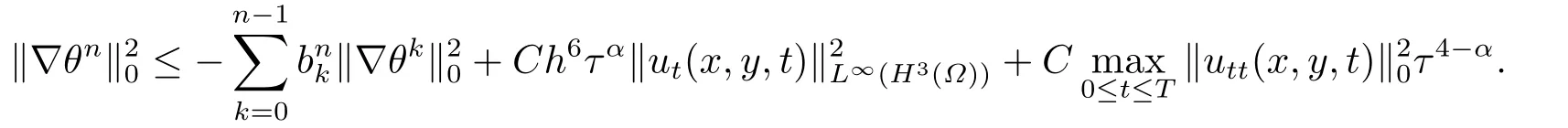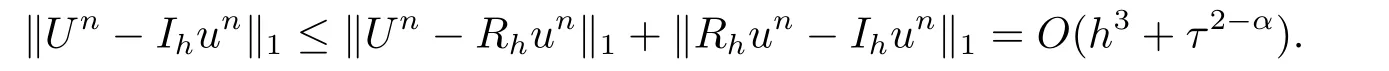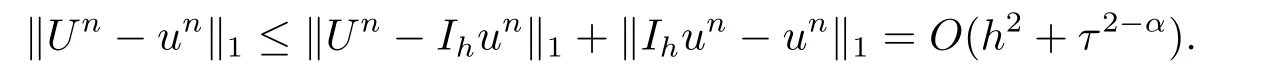二维时间分数阶扩散方程的Hermite型矩形元的超收敛分析
2019-06-27王萍莉牛裕琪赵艳敏王芬玲史艳华
王萍莉,牛裕琪,赵艳敏,王芬玲,史艳华
(许昌学院数学与统计学院,河南 许昌461000)
1.引言
本文考虑如下二维时间分数阶扩散方程(TFDE)

其中Ω ⊂R2是x-y平面上具有Lipschitz连续边界∂Ω的有界凸区域,u0(x,y)和f(x,y,t)是给定的适当光滑函数,为Caputo导数,其定义如下

其中Γ(·)是Gamma函数.
分数阶偏微分方程(FPDEs)是传统模型的扩展,基于分数微积分的定义发展起来的,因而根据定义的方式通常分为时间分数阶,空间分数阶及时空分数阶偏微分方程.随着FPDEs的不断发展,可以发现其在越来越多的领域内均有重要的应用[1−4],故而人们对其日益重视.从分数阶导数的定义知道其具有非局部性质,因而相对于整数阶方程来说,分数阶偏微分方程在声波衰减,物质记忆及遗传性质,连续时间随机游走过程等方面具有更明显的优势.但对于大多数FPDEs来说,寻找它们的解析解比较困难,因而寻找其有效的数值求解方法成了众多学者研究的热点之一.针对时间分数阶偏微分方程(TFPDEs)的数值方法大致分为直接数值算法和间接数值算法.早期关于TFPDEs的处理常常采用间接方法,将其转化为积分微分方程进行求解[5−6].直接方法是对时间分数阶导数进行直接逼近的数值方法[7−9],由于直接方法实施起来较直接简便,因而深受研究者的关注,其中最常见的一种格式即为L1逼近方法.
关于TFPDEs人们研究了多种数值求解方法,如文[1,8,10-11]中考虑了其有限差分方法,文[12-13]中采用了谱方法,文[15-21]考虑了其有限元方法,除此之外还有许多其他的数值求解方法[22−23].关于有限元方法,在整数阶偏微分方程方面我们己有些研究成果[24−32].其中文[24-25]分別研究了Hermite型矩形元対椭圆方程及广文神经传播方程的高精度分析,均得到了超逼近結果.文[29]中提出了Ritz投影与插值算子相结合的技巧,同时该技巧也被应用于其他方程[31−32],也得到较为理想的结果.
本文在空间和时间部分分别采用Hermite型矩形有限元方法及L1逼近格式,针对TFDE 建立了一个无条件稳定的全高散逼近格式,利用投影与插值算子相结合的技巧,并巧妙的处理分数阶导数对其进行了高精度数值逼近.首先,利用L1逼近的性质及数学归纳法证明了其逼近格式的稳定性; 其次,基于Hermite型矩形元的积分恒等式结果,建立了插值和Ritz投影之间在H1模意义下的超收敛分析; 进而,利用插值与投影相结合,得到了超逼近结果; 最后,借助于插值后处理技术导出了整体超收敛结果.
2.单元构造及全离散格式
设Γh是Ω上的一族正则的矩形剖分及任意K ∈Γh,设其四个顶点坐标分别为a1(−1,−1),a2(1,−1),a3(1,1),a4(−1,1),平行于x轴和y轴的边分别为边长分别为2hx,K,2hy,K,记其中hK是单元K的最大直径.设=[−1,1]×[−1,1]为平面ξ-η上的参考单元,记为的四个顶点.我们定义有限元如下
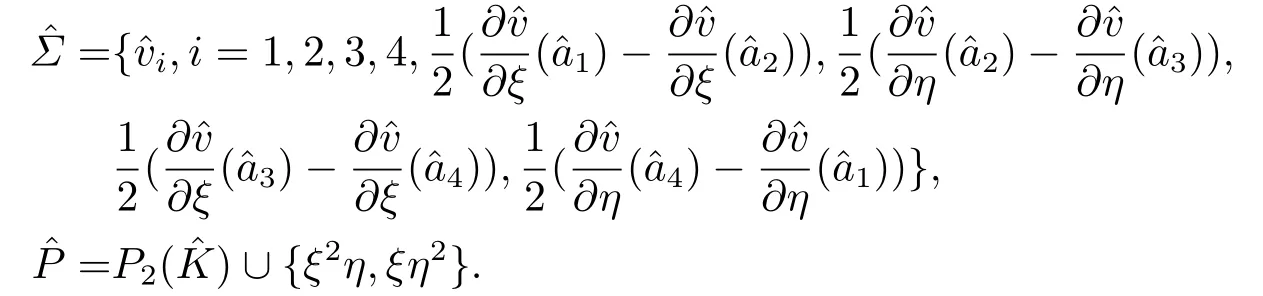
则相应的插值函数为
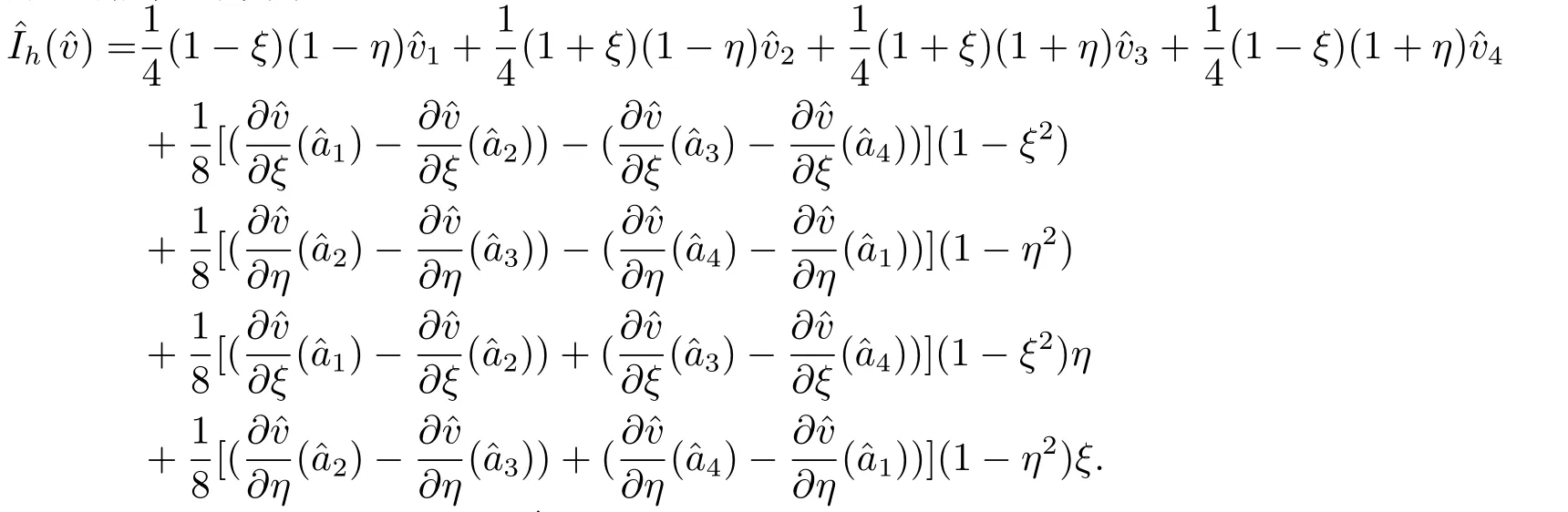
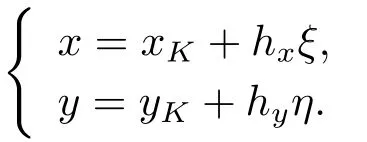
然后,我们定义相应的有限元空间V h
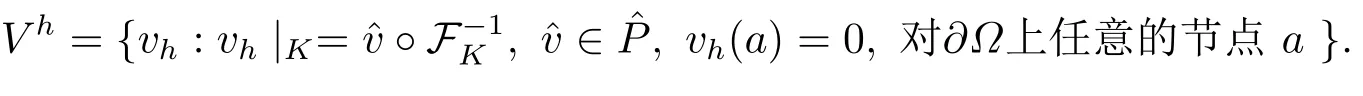
并且,由文[24]可知,若u ∈H4(Ω),则有

全文中,C是一个不依赖于h和τ的常数,在不同的地方可以取不同的值.
则(1.1)的变分形式为: 求u:(0,T]→H10(Ω)满足

接下来,先将区间[0,T]分成N个相等的子区间: 0=t0< t1< ··· < tN=T,时间步长为τ=T/N且tn=nτ,n=0,1,··· ,N.对(0,T]上的光滑函数φ,定义
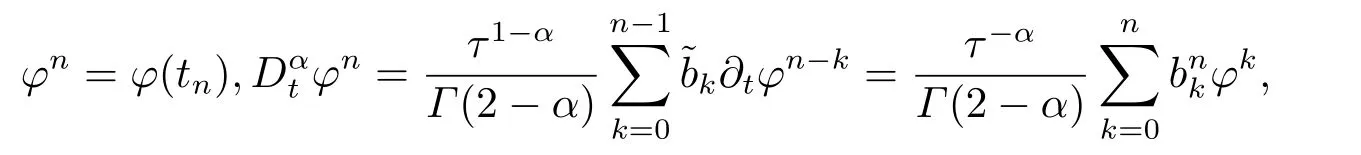
其中

由于bnk=[(n −(k −1))1−α−(n −k)1−α]−[(n −k)1−α−(n −(k+1))1−α]和φ(k)=(n −k)1−α−(n −(k+1))1−α在0 基于Hermite型矩形元和L1法,则(2.2)的全离散逼近格式为: 对于给定的Un−1,求Un∈V h满足 其中Rh:H10(Ω)→Vh是Ritz投影算子,定义如下 并且,根据文[33],有 本节中,我们将研究全离散格式的稳定性,并给出相应的超逼近和超收敛结果. 首先我们给出定理3.1,它表明全离散格式是无条件稳定的. 定理3.1设Un为(2.4)的解,则有 其中C1=max{Γ(2−α),(1−α)−1Tα}. 证在(2.4)中令vh=Un,则有 注意到DαtUn的定义,可得 利用Cauchy-Schwarz不等式及(3.3),并注意到∥∇Un∥20≥0,bnk<0(0≤k 即有 下面利用数学归纳法证明(3.1)式成立.当n=1时,注意到−b10=1,由(3.4)式可得 定理成立. 假设n ≤s时定理成立,下证n=s+1时定理成立. 定理3.1得证. 其次,基于分析需要,我们先给出下面几个引理. 引理3.1对任意的u ∈H10(Ω)∩H4(Ω),有∥Rhu −Ihu∥1≤Ch3∥u∥4. 证注意到(2.1)和(2.5)式,易得 再利用H10(Ω)空间中的模等价关系,引理3.1得证. 引理3.2[7]设φk≥0(k=1,···),φ0=0,γ >0,其满足则有 引理3.3[17]设为Ω上的一序列函数,可得 为了得到超逼近和超收敛结果,我们首先给出一些记号和误差方程.记联立(2.2)和(2.4),我们可得如下误差方程 定理3.2设un,Un分别为(2.2)和(2.4)在t=tn时刻的解.对任意的t ∈(0,T],若u(x,y,t)∈H4(Ω),ut(x,y,t)∈H3(Ω),utt(x,y,t)∈L2(Ω),以及任意的正整数1≤n ≤N,则有 证在(3.5)中,令vh=θn,则有 注意到(2.5),可知(∇ρn,∇θn)=0,因此我们有 借助于Dαtθn的定义,我们得到如下等式 由引理3.3可得 由Cauchy-Schwarz不等式及(2.3),(3.9)式右端的第二项可以估计为 由引理3.2,上式则得 利用(2.6)和(3.13),可得L2意义下的最优误差估计 接下来,为了估计∥θn∥1,我们在(3.5)中令vh=Dαtθn,则有 利用引理3.3,(3.15)的左端可变形为 对(3.15)右端的每一项进行估计. 由Cauchy-Schwarz不等式和(2.6),我们有 由投影的定义,可得 由(2.3),则有 利用引理3.2和上式,我们可得到超逼近结果 由(3.13)和(3.20),则有 由引理3.1和(3.21)及三角不等式,易得 又借助于上式及插值性质,可得 定理3.2得证. 为了得到整体超收敛,我们将相邻的九个单元合并成一个大单元,且定义插值算子满足 其中,Q3为双三次的多项式空间,C(¯e)为¯e的连续函数空间,Zi,i=1,2,··· ,16,为这九个单元的所有顶点. 引理3.4[24]设u ∈H4(Ω),则上述定义的插值算子满足 其中Sh3为双三次有限元空间. 定理3.3在定理3.2的条件下,我们有 证根据定理3.2及(3.23)-(3.25)得 则定理得证.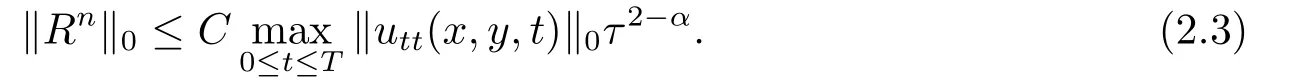
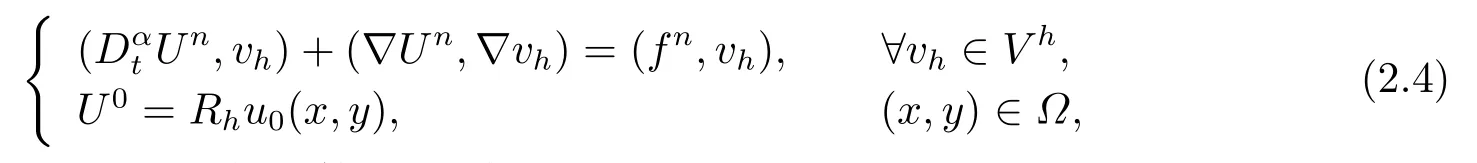

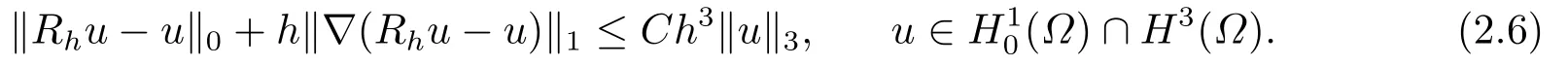
3.稳定性,超逼近和超收敛分析