矩形张量奇异值的S-型包含集
2019-06-27桑彩丽赵建兴
桑彩丽,赵建兴
(贵州民族大学数据科学与信息工程学院,贵州 贵阳550025)
1.引言
令R(C)为实(复)数域,p,q,l,m,n为正整数,l=p+q,m,n ≥2且N={1,2,··· ,n}.记A=(ai1···ipj1···jq),若
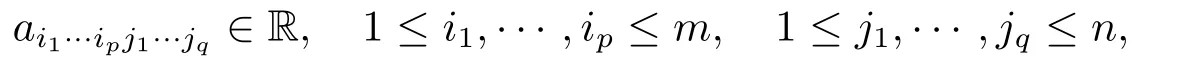
则称A为一个(p,q)阶m×n维实矩形张量[1−4],记作A ∈R[p,q;m,n].若存在数λ ∈C和非零向量x=(x1,x2,··· ,xm)T∈Cm{0},y=(y1,y2,··· ,yn)T∈Cn{0}满足方程组:

则称λ为A的奇异值[3],x和y为相应于λ的左、右特征向量,其中Axp−1yq和x[l−1]为m维向量,它们的第i个分量分别为

Axpyq−1和x[l−1]为n维向量,它们的第j个分量分别为
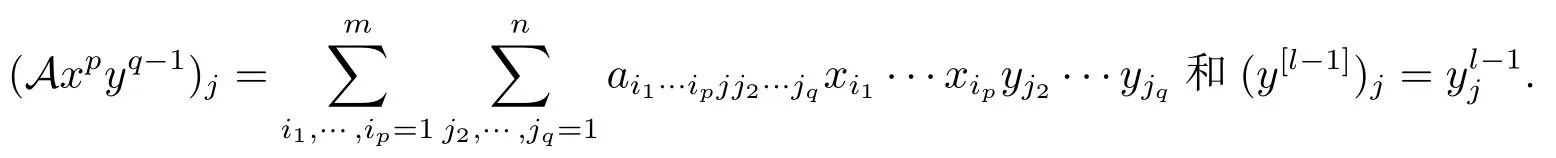
记σ(A)为A的所有奇异值组成的集合.
矩形张量的奇异值在固体力学中的强椭圆性条件[5−7]和量子力学中的纠缠问题[8]等诸多领域有着广泛的应用背景.最近许多学者对矩形张量的奇异值进行了定位,给出了一些奇异值包含集[9−13],其中ZHAO和LI于2018年在文[11]中给出了如下Gergorin-型奇异值包含集:
定理1.1[11]设A=(ai1···ipj1···jq)∈R[p,q;m,n],则

其中
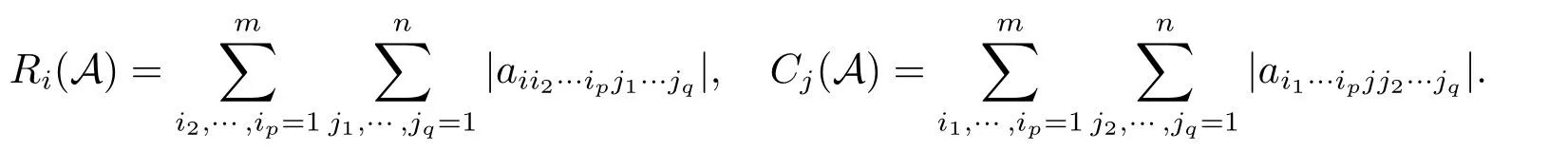
弹性张量是一个p=q=2且m=n=2或3的实张量,其在非线性弹性材料中有着重要应用[5−7].受这些应用背景的激励,文[11]就m=n这种情形给出了矩形张量奇异值的一个Brauer-型包含集:
定理1.2[11]设A=(ai1···ipj1···jq)∈R[p,q;n,n],则
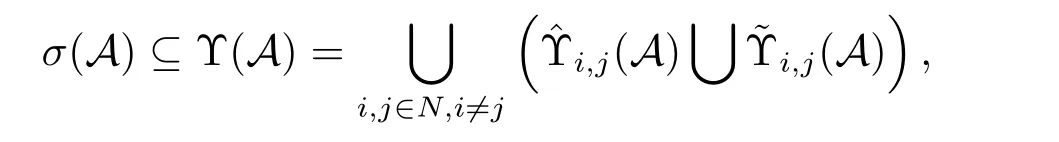
其中

和

并证明了Υ(A)⊆Γ(A).
为了减少计算量,文[12]利用指标集N的一个划分: 非空真子集S及其补集给出了张量奇异值的一个S-型包含集.
定理1.3[12]设A ∈R[p,q;n,n],S为N的非空真子集,为S在N中的补集,则

本文在文[11-12]的基础上继续考虑矩形张量A的奇异值定位问题,利用N的非空真子集S及其补集和分类讨论思想,并结合不等式放缩技巧给出A的新的S-型奇异值包含集,改进了定理1.1、定理1.2和定理1.3的结果.
2.主要结果
设矩形张量A=(ai1···ipj1···jq)∈R[p,q;n,n],S为N的非空真子集,记

且
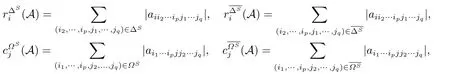
则对任意i,j ∈N,有

定理2.1设A=(ai1···ipj1···jq)∈R[p,q;n,n],S为N的非空真子集,为S在N中的补集,则
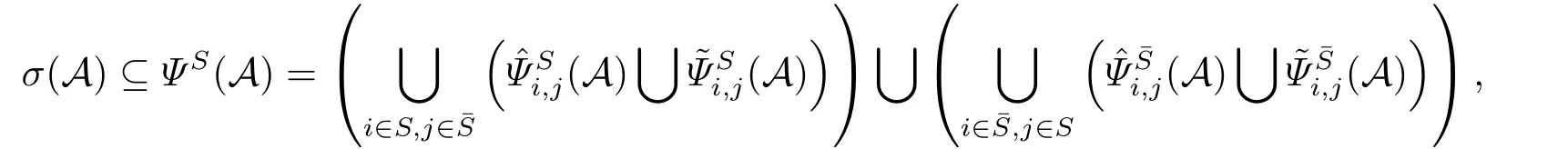
其中
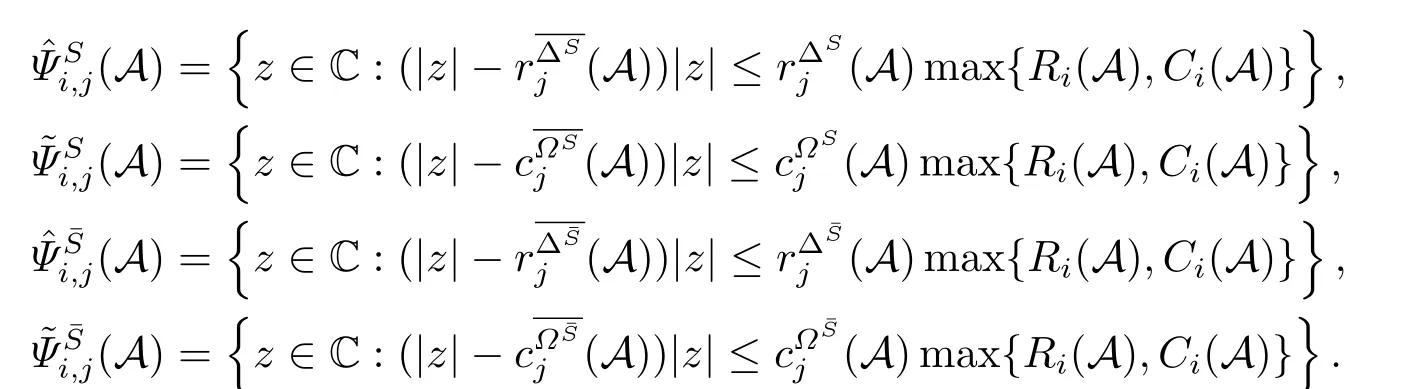
证设λ为A的奇异值,x=(x1,x2,··· ,xn)T∈Cn{0}和y=(y1,y2,··· ,yn)T∈Cn{0}为其对应的左、右特征向量.设
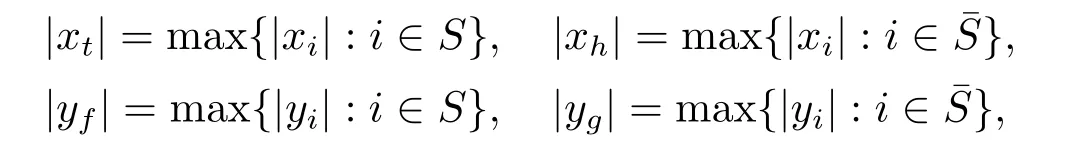
且
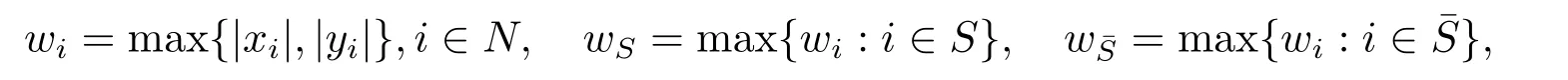
则|xt|和|xh|中至少有一个为正数,|yf|和|yg|中至少有一个为正数.下面分四种情形证明.
情形1: 假设wS=|xt|,w¯S=|xh|.
情形1.1:设|xh|≥|xt|,此时|xh|=max{wi:i ∈N}.由(1.1)式的第h个方程
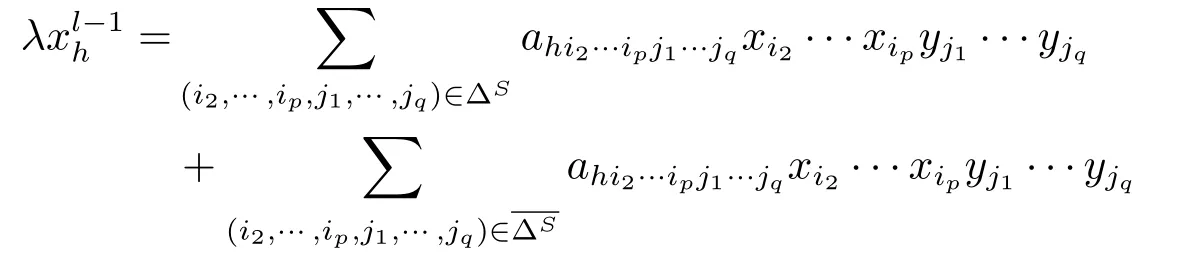
得


即

若|xt|=0,则由|xh|>0得进一步可得

若|xt|>0,则由(1.1)式的t个方程

可得

即

将(2.1)式和(2.2)式相乘,并消去|xt|l−1|xh|l−1>0,可得
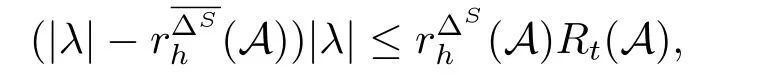
情形1.2:若|xt|>|xh|,此时|xt|=max{wi:i ∈N}.应用类似于情形1.1的证明,可得

应用类似于情形1的证明,容易完成下面三种情形的证明.
结合情形1、情形2、情形3和情形4,可知结论成立.证毕.
下面对定理1.1、定理1.2、定理1.3和定理2.1中的奇异值包含集进行比较.在此之前,先给出一个引理.
引理2.1[14]设a,b,c ≥0 且d>0,则

定理2.2设A ∈R[p,q;n,n],S为N的非空真子集,为S在N中的补集,则由定理2.1给出的奇异值包含集ΨS(A)比由定理1.1、定理1.2和定理1.3给出的包含集精确,即

证由定理1.2知Υ(A)⊆Γ(A).易知ΥS(A)⊆Υ(A).因此仅需证明ΨS(A)⊆ΥS(A),即证明: 对于任意的z ∈C,若z ∈ΨS(A),则z ∈ΥS(A).设z ∈ΨS(A),则有


下面分两种情形给出z ∈ΥS(A)的证明.
情形1:若rv∆S(A)max{Ru(A),Cu(A)}=0,则rv∆S(A)=0,或max{Ru(A),Cu(A)}=0.
情形1.1:若rv∆S(A)=0,则avu···uu···u=0,rv∆S(A)=rvu(A)且
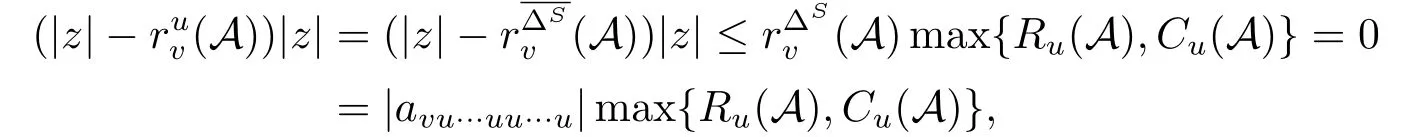
情形1.2:若max{Ru(A),Cu(A)}=0,则
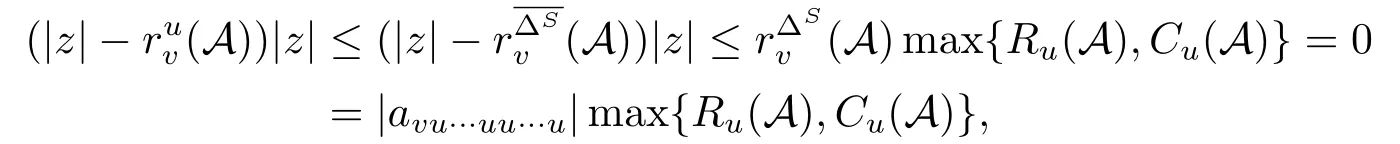
情形2:若rv∆S(A)max{Ru(A),Cu(A)}>0,则由(2.3)式得

由(2.4)式得

或

情形2.1:令a=|z|,b=rv∆S(A),c=rv∆S(A)−|avu···uu···u|和d=|avu···uu···u|.若(2.5)式成立且d=|avu···uu···u|>0,则由引理2.1中1)得

再由(2.4)式得
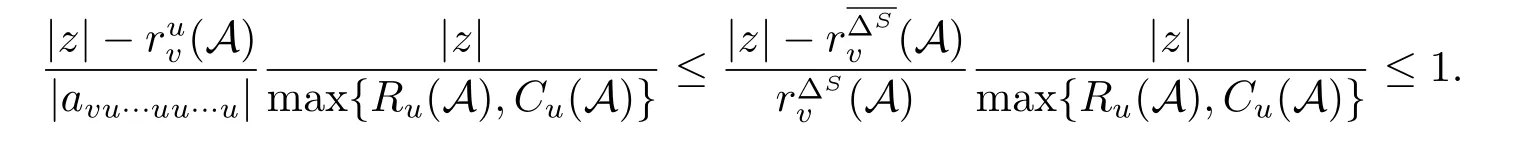
由此得


得
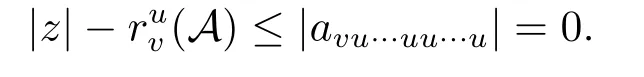
由此得

情形2.2:若(2.6)式成立,即|z|≤max{Ru(A),Cu(A)},这里仅证明当

时,z ∈ΥS(A).
若|z|≤max{Ru(A),Cu(A)}=Ru(A)且|auv···vv···v|>0,则由引理2.1中1)得

由|z|>Rv(A)和引理2.1中2)得

由(2.4)式、(2.7)式和(2.8)式得

即

若|z|≤max{Ru(A),Cu(A)}=Ru(A)且|auv···vv···v|=0,则由
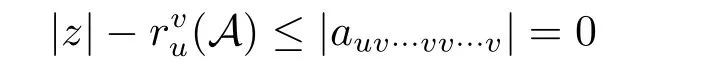
和

若|z|≤max{Ru(A),Cu(A)}=Cu(A),类似地,可得

和

证毕.
3.数值例子
本节给出两个数值算例验证第二部分的结果.
例3.1设矩形张量A=(ai1i2j1j2)∈R[2,2;3,3],其中a1121=2,a1131=a1222=5,a2111=4,a2212=6,a2232=1,a3111=a3313=8,a3222=9,a3323=10,其余aijkl=0.
下面对A的所有奇异值进行定位.取S={3},此时={1,2}.由定理1.1得

由定理1.2和定理1.3得
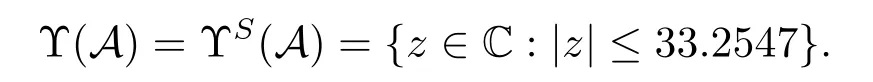
由定理2.1得

矩形张量A的奇异值包含集ΨS(A),ΥS(A),Υ(A),Γ(A)和所有奇异值见图3.1,其中Γ(A),Υ(A)和ΥS(A),ΨS(A)分别用点线、虚线和实线边界标出,所有奇异值用“+”号标出.由图3.1可以看出:σ(A)⊆ΨS(A)⊂ΥS(A)⊆Υ(A)⊂Γ(A).
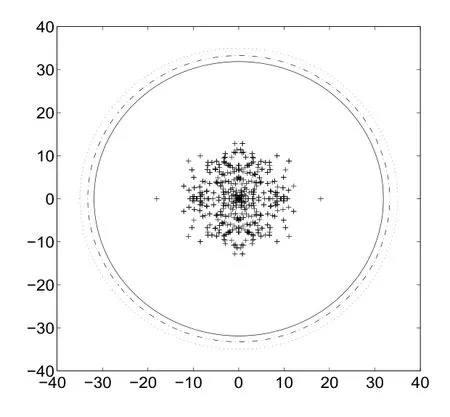
图3.1 奇异值包含集的比较

图3.2 ΨS(A)和A的所有奇异值
例3.2设矩形张量A=(ai1i2j1j2)∈R[2,2,2,2],其中a1111=a1112=a1222=a2112=a2121=a2221=1,其余aijkl=0.经计算,A的所有奇异值为±3,±1.6774±0.6722i,±1.2452±0.6322i,±1.1417±0.2018i,±1.0682±1.2175i,±1,±0.8599±0.5072i,±0.8226,±0.3373±1.8125i,±0.2090±1.0372i,±0.1378±1.2530i,0.
下面对A的所有奇异值进行定位.取S={1},此时={2}.由定理2.1得
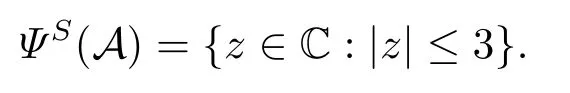
矩形张量A的奇异值包含集ΨS(A)和所有奇异值见图3.2,其中ΨS(A)用实线边界标出,所有奇异值用“+” 号标出.由图3.2可以看出,ΨS(A)恰好包含了A的所有奇异值.
