具有插队和止步行为的M/M/1/m+1排队系统的等待时间分析
2019-06-27张元元吴文青唐应辉
张元元吴文青唐应辉
(1.西南科技大学理学院,四川 绵阳621010; 2.可视化计算与虚拟现实四川省重点实验室,四川 成都610068; 3.四川师范大学基础学院,四川 成都610068)
1.引言
在日常生活中存在着大量服务和被服务的现象,当到达的顾客不能立即得到服务的情况下就出现了排队现象.比如在超市购物的顾客等待收银台人员对其进行结账服务、银行取款时的顾客等待柜台人员对其办理相关业务、出现故障的机器等待修理工来修理、电话咨询服务中电话占线的问题.然而,当排队等待的队列过长,有些顾客可能会不进入系统,有些顾客可能会选择插队.例如,当处于下课高峰期时,来食堂打饭的同学总是试图找到队列前面他认识的同学来完成插队,从而以较短时间完成服务离开排队系统.然而有些同学会直接放弃食堂吃饭选择其他方式就餐.当医院出现较多排队挂号的病人时,一些挂号者会试图插队尽快完成挂号,从而达到以相对更早的时间就诊的目的,或直接选择其他医院.
1987年,Larson[1]从社会公正现象以及社会心理学的角度将插队行为引入到排队系统中,并使用“slips” 和“skips”来具体描述具有插队行为的排队系统.Kleinrock[2],Afeche和Mendelson[3],以及Lui[4]分析队列中的顾客其具体的位置由顾客支付金钱多少来决定的排队模型.通过引入费用函数,作者推导出顾客需支付多少的最优取值.另外,Yechiali等人[5−7]根据实际情况,提出了多队列轮询的以色列排队模型.该模型中的顾客可以根据每次服务员服务完某个顾客后,选择一个对其有利的队列进行排队等待服务.2012 年,余玄少妙[8]从顾客是否履行社会公德的角度考虑了M/M/C排队模型.利用Laplace-Stielties、负指数分布理论讨论了系统中顾客的等待时间问题,并给出了顾客等待时间上界的一个近似公式.HE和Chavoushi[9]应用矩阵分析法分析并讨论了具有插队行为的排队模型.作者将到达队列的顾客分成两类:常规顾客(normal customer)和插队顾客(interjecting customer),其中常规顾客按照到达次序进行服务.若队列中顾客数不为0,顾客到队列末尾排队等待服务.插队顾客是指新到顾客为减少个人等待时间,总是试图插队到队列的前面部分,从而以较短时间完成服务.在此基础上,作者利用矩阵分析方法给出了常规顾客和插队顾客在该排队系统中的平均等待时间的数值表达式与理论结果.
本文考虑了具有插队和止步行为的M/M/1/m+1排队系统中顾客的等待时间问题.利用负指数分布、Laplace-Stieltjes变换、全概率公式,给出了处于等待队列位置n的顾客,任意一个常规顾客和任意一个插队顾客的等待时间的表达式和数值结果,并在此基础上,讨论了相关指数随系统参数的变化情况.与文[9-10]不同的是: 当系统中服务员空闲时,顾客直接进入系统接受服务; 当系统中服务员繁忙时,到达顾客考虑到插队情形的发生,其将以概率b决定进入队列等候服务,或者以概率1−b止步系统.
2.模型描述
本文研究具有插队和止步行为的M/M/1/m+1排队系统具体描述如下
1) 顾客相继到达的间隔时间服从参数为λ的Poisson流,系统中只有一个服务员,当到达顾客遇到系统空闲,则立即接受服务,其服务时间服从参数为µ(0<µ<∞)的负指数分布.
4) 插队顾客决定插队时,其插队位置取决于等待的队列中顾客数和顾客的位置.若等待队列中的顾客数为k,并且假设等待位置上的顾客拒绝其插队行为的概率为ri.因此,插队顾客成功插队于位置i的概率为队列中k个顾客均拒绝其插队行为,插队顾客处于位置k+1上的概率为
5) 系统的最大容量为m+1,当m+1个位置均被顾客占领时,新到的顾客自动离开系统.
3.具有止步行为的M/M/1/m+1排队系统排队指标
现考虑以概率b止步的M/M/1/m+1排队系统,其状态转移图如图3.1所示.

图3.1 止步策略的M/M/1/m+1排队系统的状态转移
为了便于后面研究,记
• pn(n=0,1,...,m+1)为平稳条件下任意时刻队长为n的概率;
• qn(n=0,1,...,m)为到达且能进入系统的顾客看到有n个顾客的概率;
•为顾客在队列中的平均等待时间.根据文[10-11],可得系统稳态状态概率的方程为
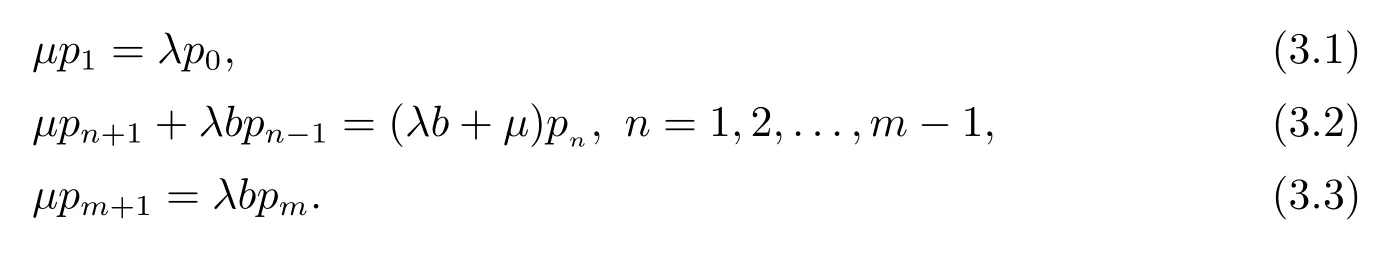
解得
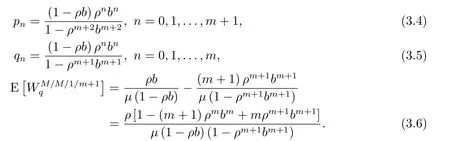
4.插队行为下顾客的等待时间分析
虽然插队行为对该排队系统的队长没有影响,但在该队列中顾客等待时间将会受到此插队行为的干扰.在本节中,我们对位置n的顾客、常规顾客与插队顾客的等待时间进行详细的讨论,同时求解出各个顾客的平均等待时间的具体表达式.在讨论之前,先给出几个需要用到的符号,记
• Wn(n=1,2,...,m): 等待位置n的顾客所需等待时间,Wn(t)=P {Wn≤t},t>0.
• W[N]: 任意一个常规顾客所需等待时间,W[N](t)=P{W[N]≤t},t>0.
进一步,定义
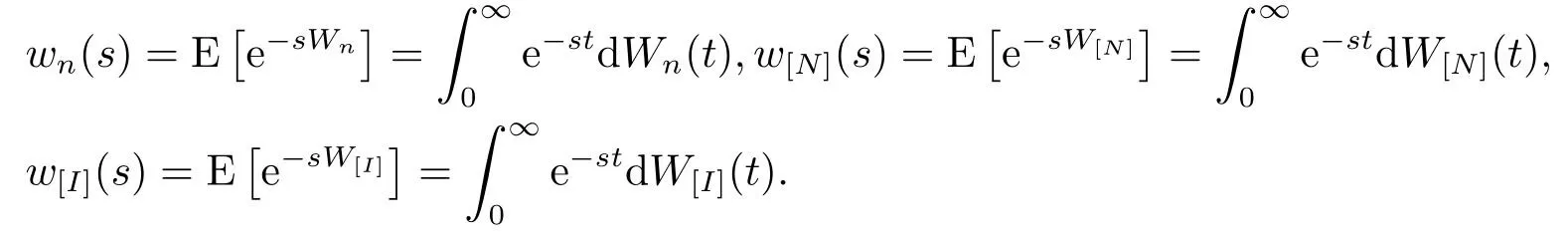
处于等待队列位置n(n=1,2,...,m)的顾客的等待时间长短与其位置的变化密切相关.而这种位置变化又取决于其自身所处位置和插队顾客剩余到达时间和顾客的剩余服务时间之间的关系.因此,对处于位置n顾客的队列序号变化做如下讨论:
情形1n=1,2,...,m −1,即顾客所处位置并非排队系统的末尾位置,可分为下面两种:
a)n →n+1: 当前繁忙的服务员服务一个顾客的剩余时间大于插队顾客的剩余到达时间;
b)n →n −1: 当前繁忙的服务员服务一个顾客的剩余时间小于下一个插队顾客的剩余到达时间.
情形2n=m,即顾客所处位置为队列末尾,这表明系统中的总顾客数已经为m+1 (一位顾客正在服务,m位顾客处于等待状态).此时新到的顾客由于容量的限制不得不直接离开系统.因此,位置m顾客的队列序号变化只能是向前移动一位.注意这里的离开不同于止步行为: 止步行为是到达顾客自己以一定的概率决定是否进入系统,而此时的离开是必然事件.
Research on corresponding views in Qingdao modern urban construction
用T1表示插队顾客在前n个位置插队成功的剩余到达时间,T2表示服务员服务一个顾客的剩余时间.记Zn=min(T1,T2)为当前位置n顾客的位置序号改变时间.于是有如下表达式:

利用负指数分布的的无记忆性,可得

进一步,得
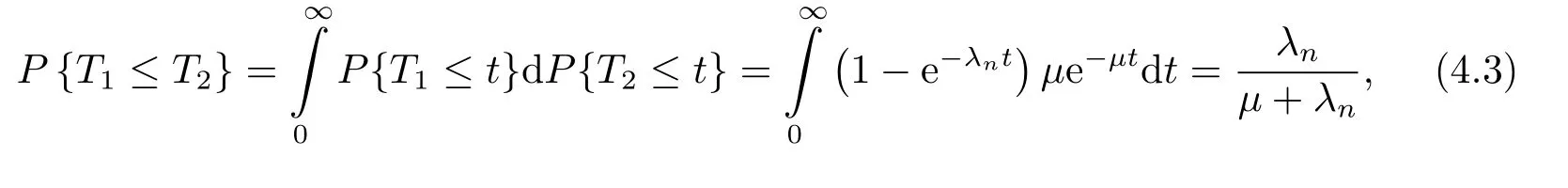

下面分3种情况讨论E[Wn]的表达式.
1)当n=1时,由全概率公式得

2)当n=2,3,...,m −1时,由全概率公式得

3)当n=m时
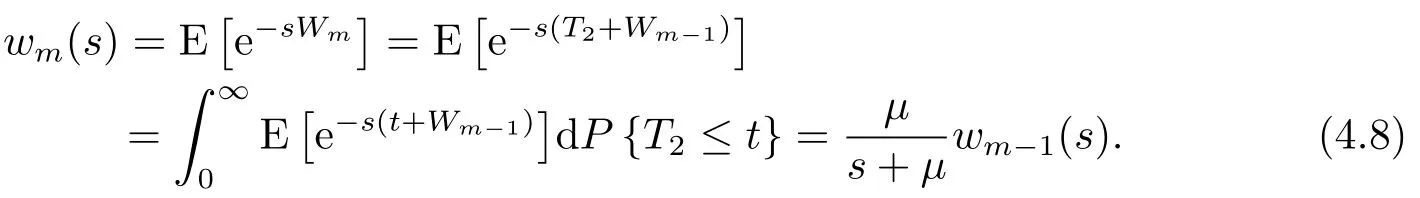
对式(4.6)-(4.8)进行简单的代数处理得

将式(4.10)反复迭代可得,

注意到w0(s)=E[e−sw0]=E[1]=1,将式(4.9)和(4.12)合并为
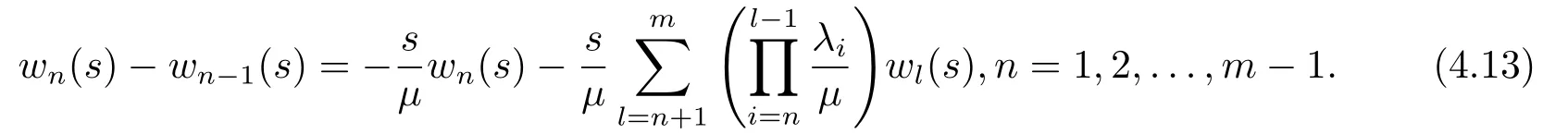
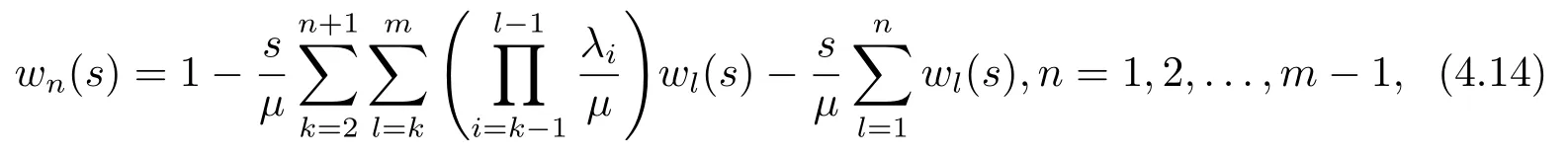


常规顾客在其所在排队系统中遵从先到先服务(FCFS)的规则,即当其到达排队系统时总是在队列的末尾排队等待服务.则平均等待时间为

结合(4.16)和(4.17)式,(4.18)转化为

当到来的插队顾客看见服务员处于忙碌状态并且队列中等待人数为n(n ≥1)时,那么它将以概率处于队列中的第k(1≤k ≤n)个位置,以概率插队不成功而排队于队列末尾.
由w[I](s)的定义和全概率公式可得
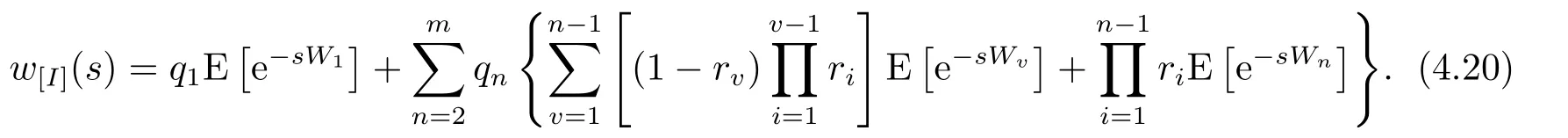
由等待位置n顾客的等待时间的相关结果,(4.20)转化为
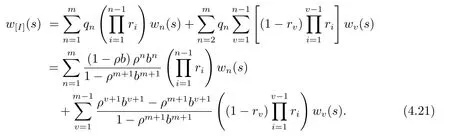
式(4.21)求导并令s=0得

5.算例分析
本节讨论排队系统中位置n顾客的平均等待时间E[Wn],n=1,2,...,m随着位置n和顾客决定插队的概率σ,顾客到来强度λ,服务时间参数µ的变化情况.进一步,讨论任意位置顾客平均等待时间E[W[N]]和插队顾客平均等待时间E[W[I]]随系统相关参数的变化趋势.所得结果见表5.1和图5.1.
算例1讨论M/M/1/45排队系统中E[Wn],(n=1,2,...),m,E[W[N]],E[W[I]]的数值结果.取λ=5.6,b=0.5,µ=3.2,σ=0.5,ri=e−1/i.
利用MATLAB 软件编写数值计算程序,其计算结果如表5.1.从表5.1可看出,在等待队列中的位置越靠后,其等待时间越长.由图5.1知在该系统中,插队顾客的等待时间期望比常规顾客的等待时间期望约小于2.7个单位.该结论不失一般性,即插队顾客等待时间期望显然小于常规顾客.
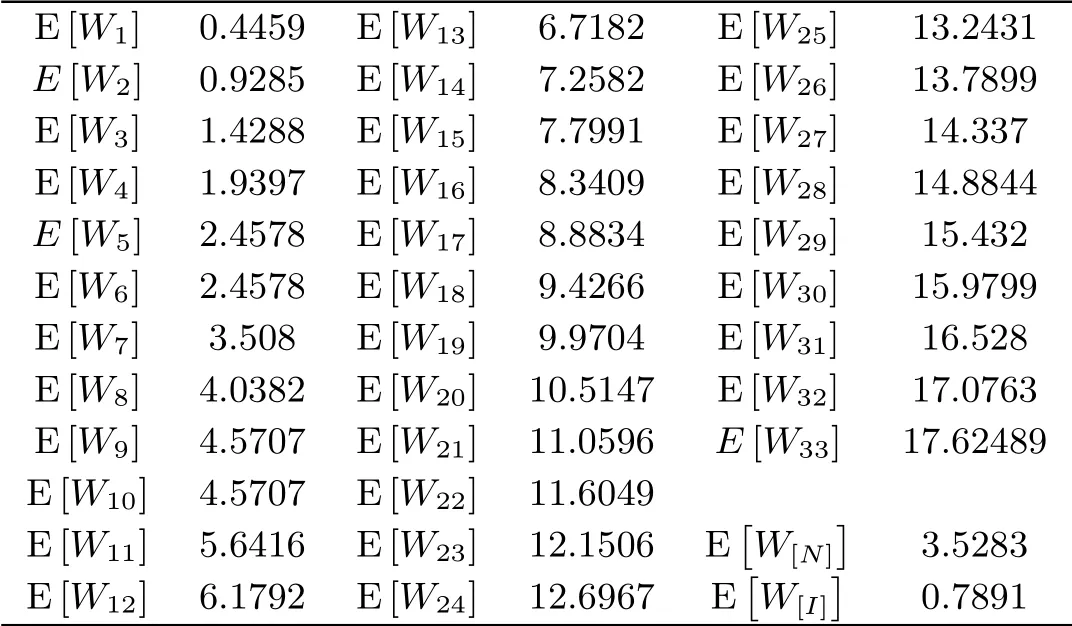
表5.1 γ 等待队列位置n的顾客的平均等待时间

图5.1 E[Wn],E[W[N]],E[W[I]]随n变化结果
算例2讨论M/M/1/42排队系统中,客流量强度和顾客插队概率σ对常规顾客的平均等待时间E和插队顾客的平均等待时间的影响情况.取µ=4.0,m=42,b=0.5,ri=e−1/i,λ从1.5变化到3.8,σ从0.32变化到0.8.利用MATLAB软件编写数值计算程序,相应的数值结果见图5.2和图5.3.

图5.2 E[W[I]]随λ和σ的变化图
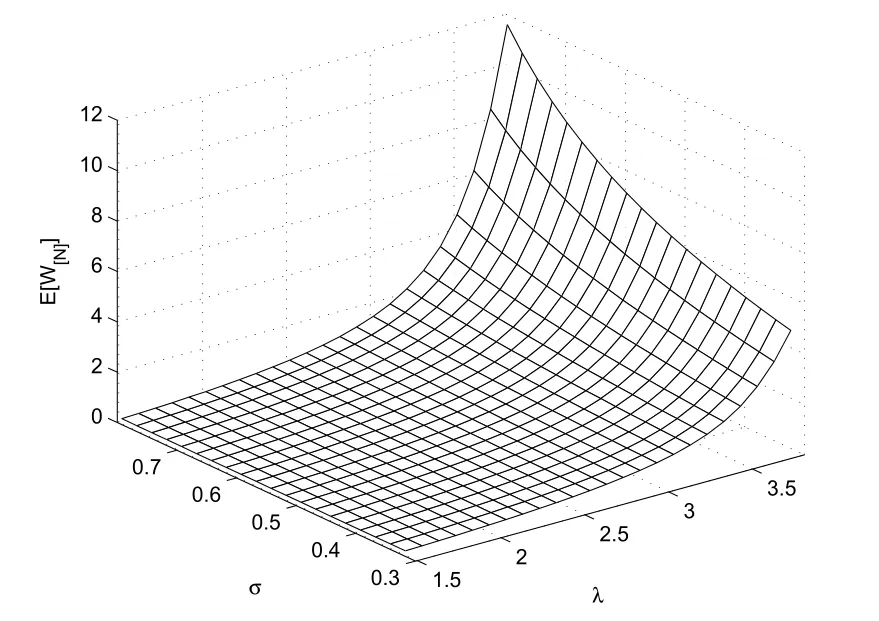
图5.3 E[W[N]]随λ和σ的变化图
从图5.2和图5.3中,可以看出当顾客到达率λ较小时,即在M/M/1/42排队系统中,顾客到来强度比较小的时候,顾客插队概率σ对E[W[N]]和E[W[I]]两者的影响就不太明显.但当顾客到达率λ增大时,顾客插队概率σ对E[W[N]]和E[W[I]]两者的影响就较为明显.与此同时,将图5.2和图5.3作比较,可以发现插队顾客的平均等待时间明显比常规顾客的平均等待时间减少了约8倍左右.
