Lagrange Type Duality and Saddle Point Optimality Criteria for Mathematical Programs with Vanishing Constraints

HU Qingjie(胡清洁)DONG Rongen(董榕恩)ZHANG Haiqi(张海琦)

( 1.Guangxi Key Laboratory of Automatic Detecting Technology and Instruments,Guilin 541004,China; 2.Guangxi Colleges and Universities Key Laboratory of Data Analysis and Computation,Guilin 541004,China; 3.School of Mathematics and Computing Science,Guilin University of Electronic Technology,Guilin 541004,China)

Abstract: In this paper,based on the structure characteristic of vanishing constraints,we propose a Lagrange type dual model which does not include the unknown index sets for the mathematical programs with vanishing constraints and establish the weak,strong duality results between the primal problem and the Lagrange type dual model under mild assumptions.We also investigate the optimality criteria of the saddle point problem to the mathematical programs with vanishing constraints under some conditions.Finally,we also verify the validity of these results through some examples.

Key words: Mathematical programs with vanishing constraints; Lagrange duality;Saddle point optimality criteria

1.Introduction

We consider the following mathematical program with vanishing constraints (MPVC for short):

wheref: Rn→R,g: Rn→Rm,h: Rn→RpandG,H: Rn→Rlare all continuously differentiable functions.In this paper,Xdenotes the feasible region of (1.1).

The mathematical programs with vanishing constraints was firstly introduced to the mathematical community in[3].It originated from the optimization topology design problems in mechanical structures.Recent researches show that it can be served as the mathematical model such as a robot path-finding problem with logic communication constraints in robot motion planning[15],scheduling problems with disjoint feasible regions in power generation dispatch[12]and mixed-integer nonlinear optimal control problems [13][17].The major difficulty in solving problem (1.1)is that it does not satisfy most of the standard constraint qualifications,such as Linear Indenpendent constraints qualification and Mangasarian-Fromovitz constraints qualification,at any optimal solution so that the standard optimization methods are likely to fail for this problem[3].It has attracted much attention in the recent years.Several theoretical properties and different numerical approaches for MPVC can be found in[1-11,14-18].However,at present,little attention is paid to dual results for the mathematical programs with vanishing constraints.Until recently,Mishra et al.[19]studied the Wolfe and Mond-Weir type dual models for the mathematical programs with vanishing constraints.They established the weak,strong,converse,restricted converse and strict converse duality results under some convexity assumptions between the primal mathematical program with vanishing constraints and the corresponding Wolfe type dual.They also derived the weak,strong,converse,restricted converse and strict converse duality results between the primal mathematical program with vanishing constraints and the corresponding Mond-Weir type dual under the corresponding convexity assumptions.However,there exist some unknown index sets in their duals.This makes it not easy to solve the dual problem.

In this paper,we propose a Lagrange type dual model and establish some saddle point optimality criteria for the mathematical programs with vanishing constraints by exploiting the structure characteristic of vanishing constraints.The weak,strong duality results between the primal problem and the Lagrange type dual model are derived under mild assumptions.The optimality criteria of the saddle point problem to the mathematical programs with vanishing constraints are established under some conditions.We also verify the validity of these results through some examples.It is worth noting that our dual model does not contain some unknown index sets.

The rest of the paper is organized as follows.In Section 2,we review some results of the MPVC.In Section 3,we give the Lagrange type dual model.In Section 4,we establish some optimality criteria of the saddle point problem to the MPVC.We close this paper with some final remarks in Section 5.

2.Preliminaries

Forx ∈X,we firstly give the following index sets for MPVC.

In order to get our Lagrange type duality,we will use the following Lagrange function for the MPVC:

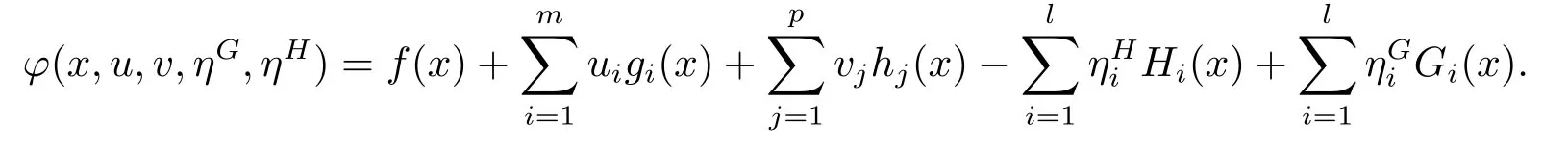
Obviously,the above Lagrange function is different from the ordinary one which is widely used in the classical nonlinear programming.

Along the lines of[3],we introduce the following modified Abadie constraint qualification(VCACQ) for MPVC by exploiting the special structure of vanishing constraints.

Definition 2.1Letx∗∈X.The VC-ACQ is said to hold atx∗,if

where

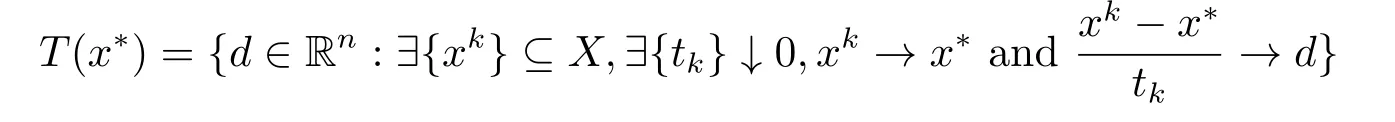
and

In [3],the following VC-KKT conditions which is weaker than the standard KKT conditions of the MPVC (1.1) were derived under the VC-ACQ.

Theorem 2.1Ifx∗∈Xis a local minimum of the MPVC(1.1)such that the VC-ACQ holds atx∗,then there existu∗∈Rm,v∗∈Rp,ηG∗∈Rl,ηH∗∈Rlsuch that

In the above theorem,x∗is called as a VC-KKT point of MPVC (1.1),and (u∗,v∗,ηG∗,ηH∗)is the corresponding multiplier vector.

The following concept of convexity plays a vital role in the subsequent analysis.

Definition 2.2LetS ∈Rnbe a nonempty set andf: Rn→R be continuously differentiable.Then,fis said to be convex atx∗∈Sif and only if for anyx ∈S,one gets

3.Lagrange Type Duality for MPVC

In this section,we will present the Lagrange type dual model for MPVC and disscuss the corresponding duality results.

Let

We firstly give the Lagrange type dual model to the MPVC (1.1) for a feasible point∈X,denoted by VCLD(),as follows.

We denote bySD()={(u,v,ηG,ηH,ρ,ν) :ui≥0,i=1,2,··· ,m,ηGi=νiHi(),νi≥0,i=1,2,··· ,l,ηHi=ρi−νiGi(),ρi≥0,i=1,2,··· ,l}the feasible set of the VCLD().Obviously,the above dual model depends on the primal MPVC (1.1).In order to make it independent of the primal MPVC,we present another duality problem (VCLD) as follows:

Remark 2.1Obviously,the above dual does not contain the unknown index sets.This implies that it is more easier to deal with the above dual than the one in [19] from algorithm point of view.

The following index sets will be used in the sequel.

Now,we establish the weak duality and strong duality theorems between the VCLD(x)and the MPVC (1.1).

The following theorem is a weak duality result,which indicates the relationship between a feasible point of the MPVC (1.1) and a feasible point of the Lagrange duality (VCLD(x)).

Theorem 3.1(Weak duality) Ifx ∈Xand (u,v,ηG,ηH,ρ,ν)∈SD(x) is the feasible points for the MPVC (1.1) and the VCLD(x),respectively,then

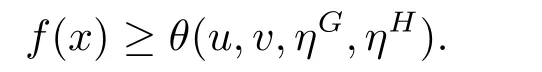
ProofIn view ofx ∈Xand (u,v,ηG,ηH,ρ,ν)∈SD(x) being the feasible points for the MPVC (1.1) and the VCLD(x),respectively,we can obtain that

The proof is completed.

Based on the above theorem,we can get easily the following three corollaries.

Corrollary 3.1Ifx ∈Xand (u,v,ηG,ηH,ρ,ν)∈XDis the feasible points for the MPVC (1.1) and the VCLD,respectively,then

Corrollary 3.2Ifx∗and(u∗,v∗,ηG∗,ηH∗,ρ∗,ν∗)is the optimal solution for the MPVC(1.1) and the VCLD,respectively,then

Corrollary 3.3If x∗and (u∗,v∗,ηG∗,ηH∗,ρ∗,ν∗) is the feasible point for the MPVC(1.1)and the VCLD,respectively,and f(x∗)=θ(u∗,v∗,ηG∗,ηH∗),then x∗and(u∗,v∗,ηG∗,ηH∗,ρ∗,ν∗) is the optimal solution for the MPVC (1.1) and the VCLD,respectively.

In order to prove the strong duality theorem,the following lemma is necessary.

Lemma 3.1If x∗is a local optimal solution of the MPVC(1.1)such that the VC-ACQ holds at x∗,then there exists(u∗,v∗,ηG∗,ηH∗,ρ∗,ν∗)which is the feasible point of VCLD(x∗).

ProofTaking into account that x∗is a local optimal solution of the MPVC (1.1) and the VC-ACQ holds at x∗,from Theorem 2.1,we can know that there are u∗∈Rm,v∗∈Rp,ηG∗∈Rl,ηH∗∈Rlsuch that(2.1)and(2.2)hold.The next object is to prove that there exist ρ∗,ν∗such that (u∗,v∗,ηG∗,ηH∗,ρ∗,ν∗) is the feasible point of VCLD(x∗).

Case 1 i ∈I+−(x∗).Since Hi(x∗) > 0,Gi(x∗) < 0,from (2.2),we know that=0,=0.According to (3.1),we may choose ρ∗i=0,ν∗i=0.

Case 2 i ∈I+0(x∗).In view of Hi(x∗) > 0,Gi(x∗)=0 and (2.2),we know that ηiG∗≥0,ηiH∗=0.From (3.1),we may choose ρ∗i=0,νi∗≥0.

Case 3 i ∈I0−(x∗).Noting that Hi(x∗)=0,Gi(x∗) < 0 and (2.2),we know thatAccording to (3.1),we may choose ρ∗i≥0,ν∗i≥0.

Case 4 i ∈I0+(x∗).In view of Hi(x∗)=0,Gi(x∗) > 0 and (2.2),we know thatis free.By using (3.1),we may choose ρ∗i≥0,ν∗i≥0.

Case 5 i ∈I00(x∗).In view of Hi(x∗)=0,Gi(x∗)=0,from (2.2),we know thatAccording to (3.1),we may choose ρ∗i≥0,ν∗i≥0.The proof is completed.

The following theorem presents a strong duality relation between the MPVC and the VCLD(x) at a local optimal solution of the MPVC.

Theorem 3.2(Strong duality) Let x∗be a local optimal solution of the MPVC (1.1)such that the VC-ACQ holds at x∗.Assume that one of the following conditions holds:

(i) φ(·,u,v,ηG,ηH) is convex at x∗for all (u,v,ηG,ηH,ρ,ν)∈SD(x∗);

(ii) f,gi(i ∈I+g(x∗)),hi(i ∈I+h(x∗)),−hi(i ∈I−h(x∗)),−Hi(i ∈I++(x∗)∪I+0(x∗)),Hi(i ∈I0−(x∗)),−Gi(i ∈I0−+(x∗)∪I0−0(x∗)∪I+−0(x∗)),Gi(i ∈I0+0(x∗)∪I0+−(x∗)∪I++0(x∗)∪I++−(x∗))are all convex at x∗.

ProofTaking into account the facts that x∗is a local optimal solution of the MPVC(1.1) and the VC-ACQ holds at x∗,from Theorem 2.1,we can know that there are u∗∈Rm,v∗∈Rp,ηG∗∈Rl,ηH∗∈Rlsuch that (2.1) and (2.2) hold.Hence,from Lemma 3.1,we know that there exist ρ∗,ν∗such that (u∗,v∗,ηG∗,ηH∗,ρ∗,ν∗) is the feasible point of VCLD(x∗).Noting that the definitions of the index sets,we know that the following equality holds:

(i) In view of the fact that φ(·,u,v,ηG,ηH) is convex at x∗for all (u,v,ηG,ηH,ρ,ν) ∈SD(x∗),we get for all x ∈Rn,

From (2.1)(3.3)(3.4),one gets

By the weak duality theorem,it follows that

Combining the above two relationships,we obtain that

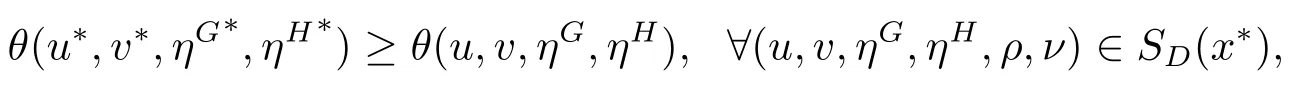
that is,(u∗,v∗,ηG∗,ηH∗ρ∗,ν∗) is a global optimal solution of the VCLD(x∗).Obviously,the optimal value of the MPVC and VCLD(x∗) is equal.

(ii) By using the convexity of

Noting that the definitions of those index sets,we obtain that

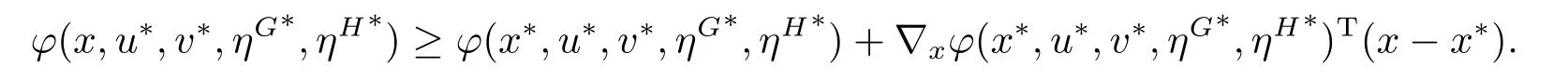
Similar to the proof of (i),a required result can be also obtained.

We will verify the validity of the Weak duality theorem and Strong duality theorem through the following example.

Example 3.1We consider the following two-dimensional MPVC problem

The feasible region of the above MPVC problem is given by

Let

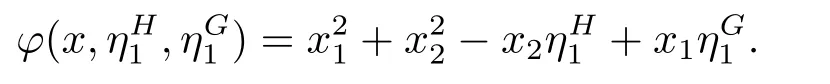
Since

is positive definite,φ(·,ηH1,ηG1) is a convex function.Hence,

For anyx ∈X,the VCLD(x) for the above MPVC problem is formulated as

In view of the fact that

we get that the weak duality theorem between the above MPVC problem and VCLD(x)holds true.

The next objective is to verify the validity of the strong duality theorem.Sincex∗=(0,0)is an optimal solution of the above MPVC problem,and VC-ACQ holds atx∗,andφ(·,ηH1,ηG1)is a convex function atx∗,by the Strong duality theorem,there existSD(x∗) such thatis a global optimal solution of VCLD(x∗) and

We now verify the validity of the above Strong duality results.Since

then the VCLD(x∗) is given by

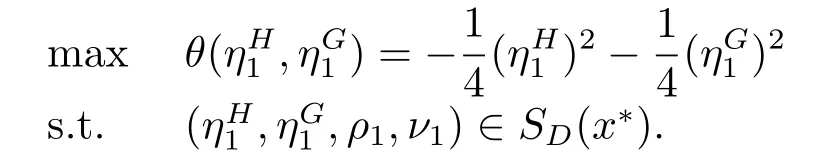
Obviously,the optimal solution of theMoreover,

4.Saddle Point Optimality Criteria for MPVC

In this section,we will discuss the saddle point optimality criteria of the MPVC (1.1).Firstly,we give the definition of the saddle point about the MPVC.That is to say,there exists a pair of (x∗,u∗,v∗,ηG∗,ηH∗,ρ∗,ν∗) withx∗∈Xand (u∗,v∗,ηG∗,ηH∗,ρ∗,ν∗)∈SD(x∗) such that

holds for allx ∈Rnand (u,v,ηG,ηH,ρ,ν)∈SD(x∗).We call (x∗,u∗,v∗,ηG∗,ηH∗,ρ∗,ν∗) as a saddle point ofφ(x,u,v,ηG,ηH).

The following theorem proposes the conditions under which an optimal solution of the MPVC generates a saddle point ofφ(x,u,v,ηG,ηH).

Theorem 4.1Ifx∗is a local optimal solution of the MPVC,and the conditions of the strong duality theorem hold,then there exists (u∗,v∗,ηG∗,ηH∗,ρ∗,ν∗)∈SD(x∗) such that(x∗,u∗,v∗,ηG∗,ηH∗,ρ∗,ν∗) is the saddle point ofφ(x,u,v,ηG,ηH).

ProofSince the conditions of the strong duality theorem hold,from Theorem 2.1,we can obtain that there areu∗∈Rm,v∗∈Rp,ηG∗∈Rl,ηH∗∈Rlsuch that (2.1) and (2.2)hold.From Lemma 3.1,we know that there existρ∗,ν∗such that (u∗,v∗,ηG∗,ηH∗,ρ∗,ν∗) is the feasible point of VCLD(x∗).In view of that the definitions of the index sets,one gets the following equality:

Similar to the proof of Theorem 3.2,from the corresponding convexity,we can also obtain for allx ∈Rn

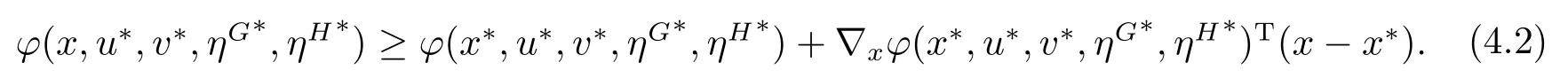
Taking into account (2.1) and (4.2),we know that the following inequality holds:

On the other hand,from (4.1) and the feasibility ofx∗,it follows that

Combining the above two relationships,we can obtain that(x∗,u∗,v∗,ηG∗,ηH∗,ρ∗,ν∗)is the saddle point ofφ(x,u,v,ηG,ηH).

The following theorem shows that a VC-KKT point of the MPVC is a saddle point ofφ(x,u,v,ηG,ηH) under some conditions.

Theorem 4.2Letx∗be a VC-KKT point of the MPVC and (u∗,v∗,ηG∗,ηH∗) be the corresponding multiplier vector.Assume that one of the following conditions holds:

(ii)φ(·,u,v,ηG,ηH) is convex atx∗for all (u,v,ηG,ηH,ρ,ν)∈SD(x∗).Then there existρ∗,ν∗such that(x∗,u∗,v∗,ηG∗,ηH∗,ρ∗,ν∗)is the saddle point ofφ(x,u,v,ηG,ηH).

ProofTaking into account thatx∗being a VC-KKT point of the MPVC and(u∗,v∗,ηG∗,ηH∗)being the corresponding multiplier vector,from Theorem 2.1,Lemma 3.1 and the definition ofSD(x∗),we know that there existρ∗,ν∗such that (u∗,v∗,ηG∗,ηH∗,ρ∗,ν∗)∈SD(x∗).

(i) Noting that the convexity of the functionsand−hj(j ∈I−h(x∗)),we can obtain that

Combing the above inequalities,(2.1) and (2.2),one gets

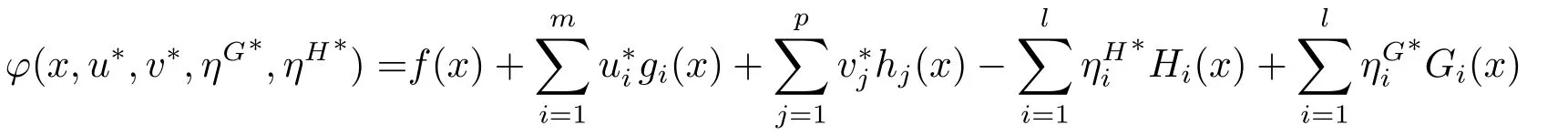
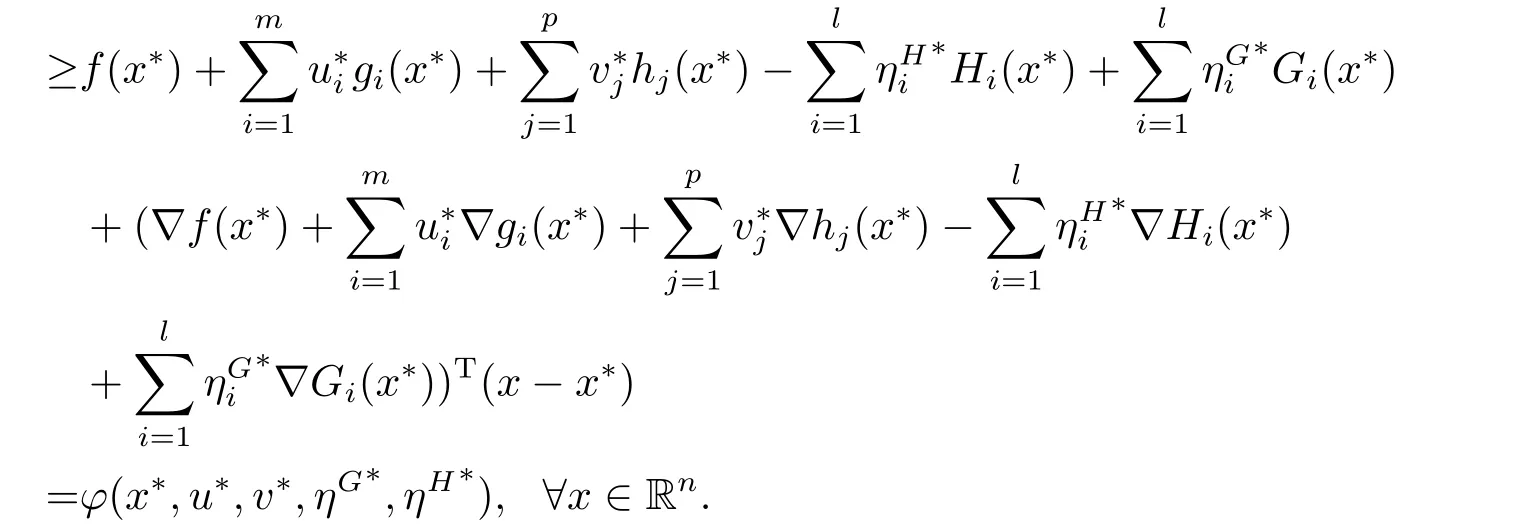
On the other hand,from (2.2),we have for all (u,v,ηG,ηH,ρ,ν)∈SD(x∗)

In view of the above two relationships,we can conclude that (x∗,u∗,v∗,ηG∗,ηH∗,ρ∗,ν∗) is the saddle point ofφ(x,u,v,ηG,ηH).

(ii) From the convexity ofφ(·,u,v,ηG,ηH) atx∗for all (u,v,ηG,ηH,ρ,ν)∈SD(x∗),we get for allx ∈Rn

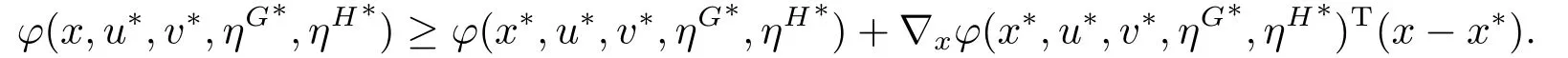
Similar to the proof of case (i),we can also conclude that (x∗,u∗,v∗,ηG∗,ηH∗,ρ∗,ν∗) is the saddle point ofφ(x,u,v,ηG,ηH).

Now,we will verify the validity of Theorem 4.1 and Theorem 4.2 through the following example.

Example 4.1We continue to consider the MPVC problem in Example 3.1.From Example 3.1,we know thatx∗=(0,0) is an optimal solution of the MPVC problem and the conditions of Strong duality theorem hold true,by Theorem 4.1,there existsuch thatis a saddle point ofφ(x,ηG1,ηH1).

We now verify the validity of the above results.Sincethen we can chooseObviously,In view of thatφ(·,ηH1,ηG1) being a convex function atx∗,one gets

The validity of Theorem 4.1 is completed.

The following object is to verify the validity of Theorem 4.2.

Sincex∗=(0,0) is an optimal solution of the MPVC problem and VC-ACQ holds atx∗,by Theorem 2.1,we can obtain thatx∗is a VC-KKT point of the MPVC andis the corresponding multiplier vector such that

Hence,from the above relationships,we can getSincef(x)=x21+x22,−H1(x)=−x2,G1(x)=x1are convex functions,by Theorem 4.2,we can conclude that there exist (ρ∗1,ν∗1)=(0,0) such thatis a saddle point ofφ(x,ηG1,ηH1).Obviously,we can also verify the validity of the above results which is obtained by Theorem 4.2 in a similar way.

5.Conclusions

In this paper,by considering the special structure of vanishing constraints,a Lagrange type dual model and some saddle point optimality criteria for the mathematical programs with vanishing constraints are studied.The weak,strong duality results between the primal problem and the Lagrange type dual model under mild assumptions are derived.The optimality criteria of the saddle point problem to the mathematical programs with vanishing constraints are investigated under some conditions.As further research work,some other dual model,like the Fenchel-Lagrange type duality,may be established by relaxing some conditions to obtain the corresponding duality results.