年龄结构乙肝传染病模型及稳定性
2019-06-27刘纪轩王改霞李学志
刘纪轩,王改霞,李学志
(1.空军工程大学航空机务士官学校基础部,河南 信阳464000; 2.信阳学院数学与信息学院,河南 信阳464000; 3.河南师范大学数学与信息科学学院,河南 新乡453007)
1.引言
世界卫生组织驻华代表处利千基博士强调,乙型肝炎和丙型肝炎均为慢性感染传染病,可能长期不出现症状,有时会长达数年或数十年.至少有60%的肝癌病例因没有及时检测和治疗病毒性乙型肝炎和丙型肝炎所致.我国约有2800万人慢性乙肝患者,肝硬化、肝癌患者中,乙型病毒性肝炎感染引起的分别高达60%-80%.
从肝炎病毒入侵到临床出现最初症状以前,这段时期称为潜伏期[1−5].乙肝潜伏期为6周~6个月,一般为3个月.潜伏期随病原体的种类、数量、毒力、人体免疫状态而长短不一.对于乙肝疾病可以采用隔离治疗,隔离期限根据医学检查结果确定.由于乙肝疾病可能长期不出现症状,且不同年龄的人对乙肝疾病的潜伏期长短、感染能力及传播能力不同,因而研究年龄结构乙肝传染病模型具有重要的实际意义.
2.模型
把总人口分为易感类、潜伏类、染病类、隔离类、免疫类,分别用S(a,t),E(a,t),I(a,t),Q(a,t),R(a,t)表示各类年龄密度函数,a为年龄,t为时间.µ(a)为年龄依赖自然死亡率,[ε(a)]−1平均潜伏周期,[α(a)]−1为平均染病周期,[g(a)]−1为平均隔离周期,b(a)为年龄依赖出生率.令感染力函数为[6]
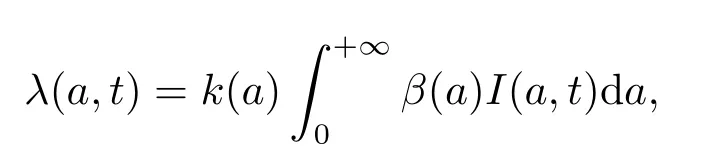
其中β(a)为年龄依赖的染病率,k(a)为年龄依赖的接触率.不考虑因病死亡,则年龄结构乙肝SEIQR传染病模型为
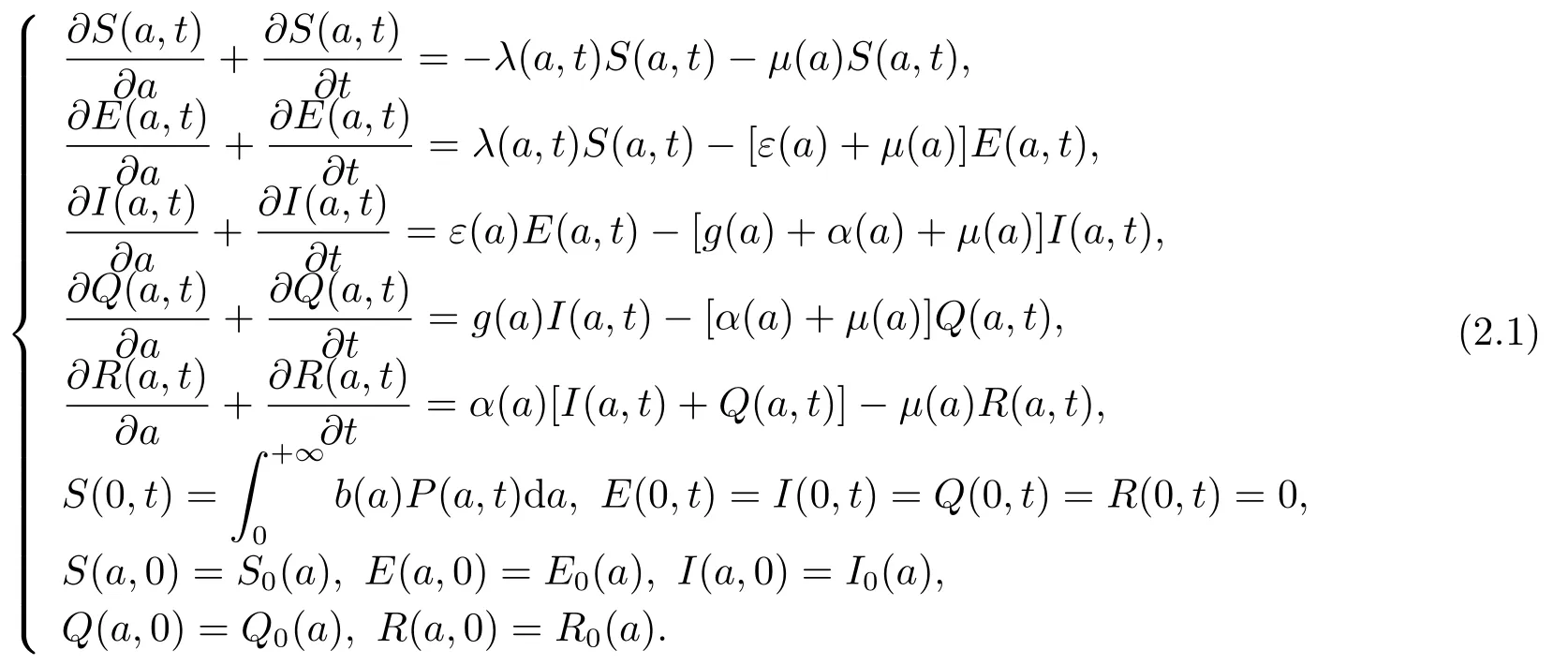
把(2.1)前四个方程相加得总人口年龄密度函数P(a,t)=S(a,t)+E(a,t)+I(a,t)+Q(a,t)+R(a,t)满足
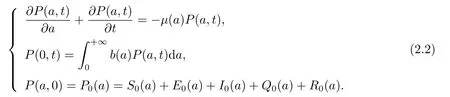
这是一个标准的Mckendrick-von Forester方程.假设所有的参数都非负[7],且

假设当个体超过一定生育年龄时b(a)=0.假设总人口处于稳定状态[8],即假设

设

则有
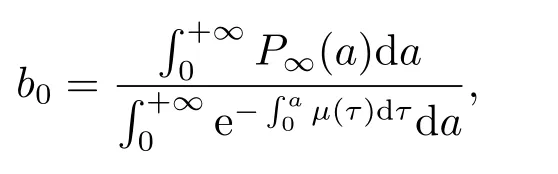
由(2.3)得

对系统(2.1) 作归一化处理[9]
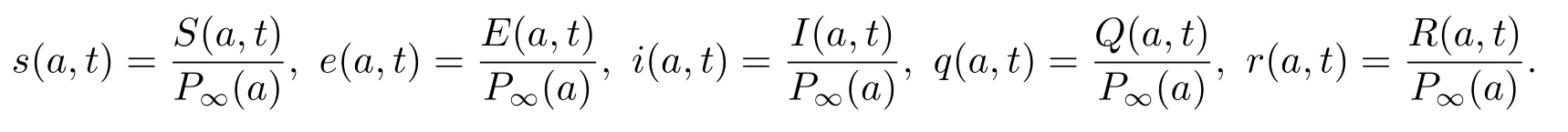
则系统(2.1) 转化为

3.无病平衡点及其稳定性
系统(2.4) 平衡解满足

易得(3.1)的无病平衡点E0(1,0,0,0,0).为讨论其稳定性,将系统(2.4)在E0处线性化[9],考虑如下形式的指数解
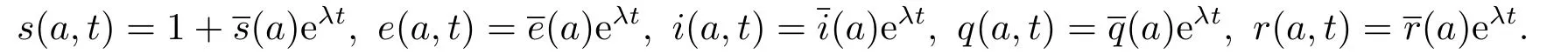
省略高阶项得

其中

为常数.由(3.2)第二个方程得

代入(3.2)第三个方程得

把(3.4)代入(3.3),两边同除以V0(其中V00) 可得特征方程为

定义基本再生数[9]ℜ0=G(0),即

则有下面的定理:
定理3.1若ℜ0<1,则无病平衡点E0(1,0,0,0,0)是局部渐近稳定的; 若ℜ0>1,则无病平衡点E0不稳定.
证注意到

当G(0)>1时,即ℜ0>1时,方程(3.5)有唯一的正实根,此时无病平衡点E0不稳定.当G(0)<1时,也即ℜ0<1时,方程(3.5)有唯一的负实根λ∗.λ∗是G(λ)=1的占优实根,事实上,设λ=x+iy是(3.5)的任意根,由于

由G(λ)的递减性得,Reλ ≤λ∗.也就是说当ℜ0<1,则无病平衡点E0(1,0,0,0,0)是局部渐近稳定的.证毕.
定理3.2若ℜ0<1,则无病平衡点E0是全局渐近稳定的.
证令

其中s(a,t)≤1,则将(2.4)式沿特征线积分得到

代入(3.7)得
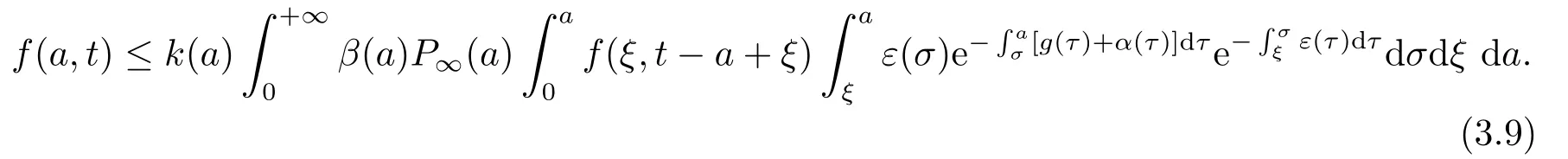
令

对(3.9)式两边取t →+∞时的上极限,由Fatou引理得

令C是常数,
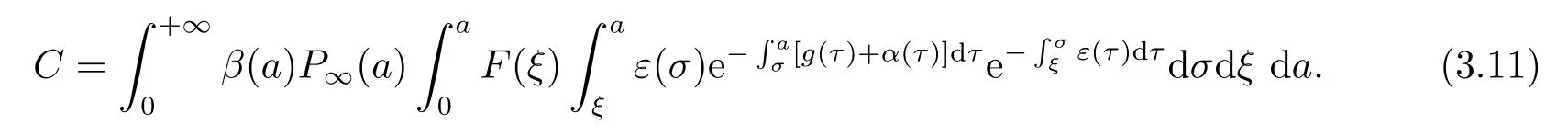
则(3.10)式变为

代入(3.11)得
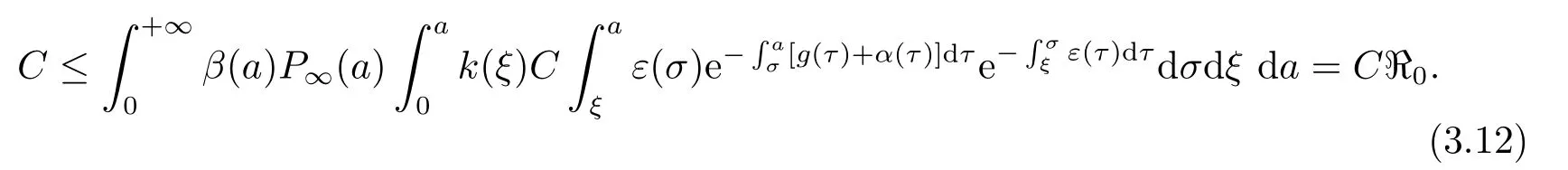
从(3.12)式可以看出,若ℜ0<1,则C=0,从而F(a)=0,因此

从而由(3.8)式得

从而有limt→+∞s(a,t)=1.
故若ℜ0<1,则无病平衡点E0是全局渐近稳定的.
4.地方病平衡点的存在性和稳定性
前面得到当ℜ0>1时,无病平衡点不稳定.实际上此时存在地方病平衡点.
定理4.1当ℜ0>1时,系统(2.4)存在唯一的地方病平衡点.
证若系统(2.4)存在地方病平衡点E∗(s∗(a),e∗(a),i∗(a),q∗(a),r∗(a)),则满足
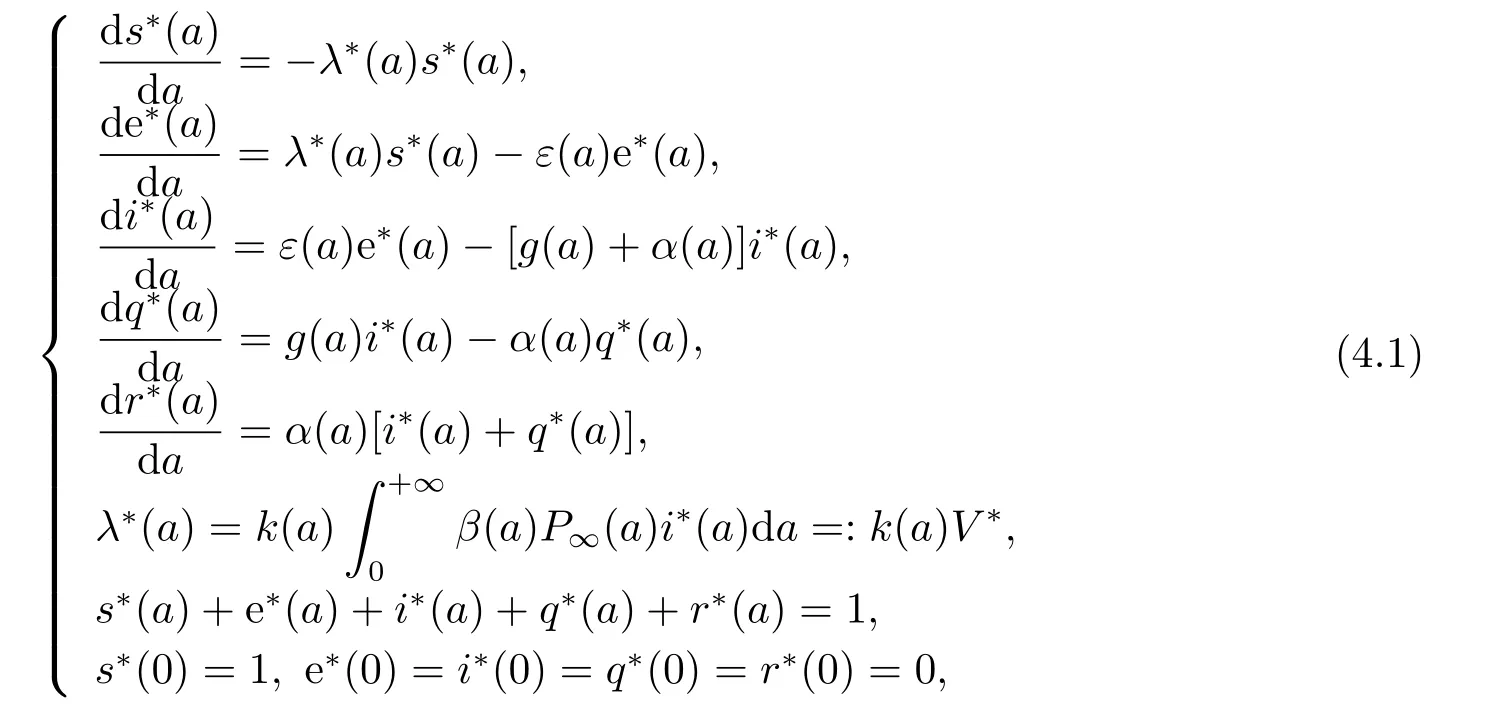
其中
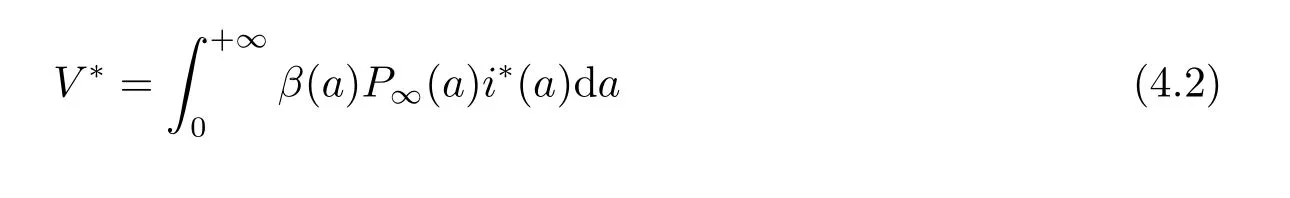
为常数,显然每一个正数V ∗对应唯一的地方病平衡点.由(4.1)中的前两个式子得

将i∗(a)代入(4.2)后,两边同除以V ∗(其中V ∗0),有

若(4.4)有一个正解V ∗,那么系统(2.4)就存在地方病平衡点.又s∗(a)+e∗(a)+i∗(a)+q∗(a)+r∗(a)=1,且s∗(a)>0,则i∗(a)<1.对任意的V ∗>0,有

其中N是总人口,β+=max{sup[0,+∞)β(a)}.
若V ∗=β+N,则H(β+N)<1.又H(V ∗)是关于V ∗的单调递减连续函数,因此若H(0)=ℜ0>1则H(V ∗)=1在区间(0,β+N)上存在唯一正解.即当ℜ0>1时,系统(2.4)存在唯一的地方病平衡点.证毕.


令

求解(4.6) 得
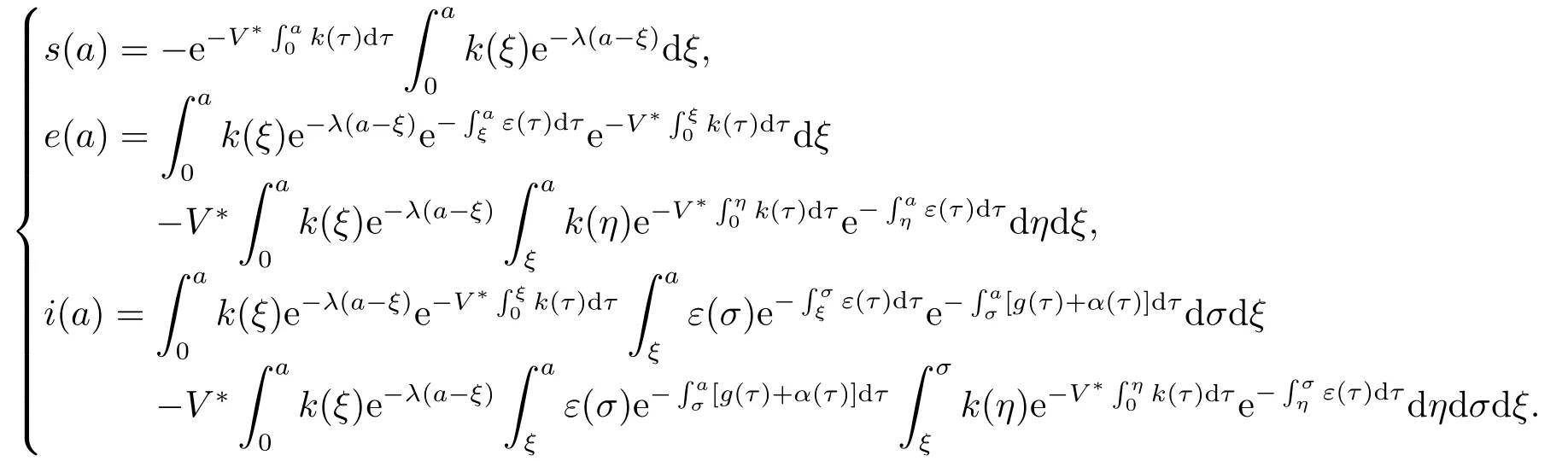
将i(a)代入T(λ)换序并整理得
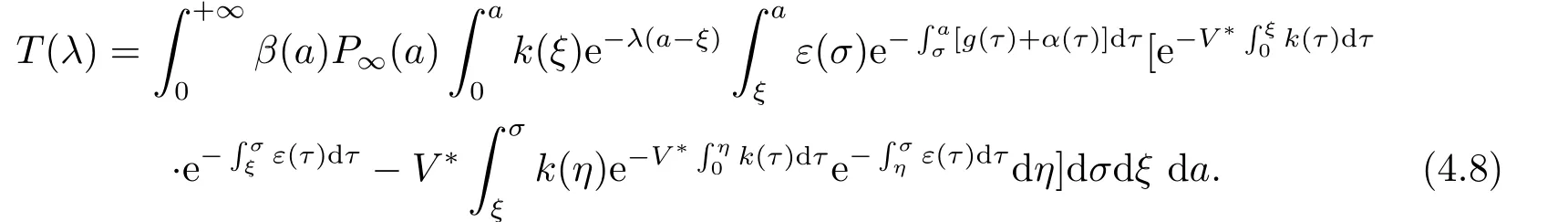
若

则有
定理4.2若条件(4.9)满足,则
1)T(λ)关于λ递减且当λ →+∞时趋近于0;
2)T(0)<1.
证1) 若条件(4.9)满足,则可得到(4.8)式中括号内式子大于零,因而T(λ)≥0关于λ指数递减,且当λ →+∞时T →0.
2) 令λ=0得

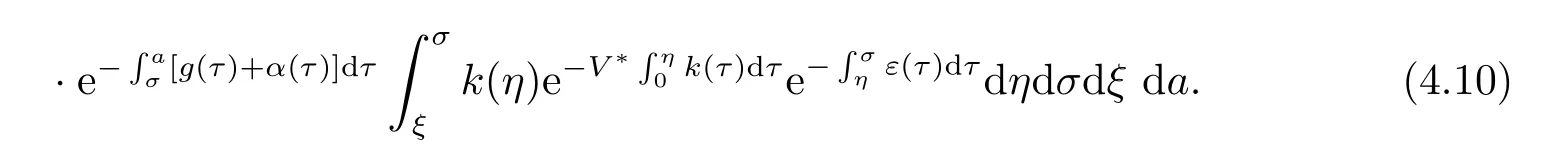
由(4.4)可以看出上式第一个积分等于1.因此,T(0)<1.证毕.
定理4.2及(4.8)说明方程T(λ)=1,也就是(4.7)有唯一的负实根且所有的复根实部都小于这个负实根.因此有
定理4.3假设(4.9)成立,则系统(2.4)的地方病平衡点局部渐近稳定.
