一类具有饱和发生率和复发的随机SIRI模型的稳定性
2019-06-27穆宇光徐瑞
穆宇光,徐瑞
( 陆军工程大学石家庄校区军政基础系,河北 石家庄050003)
1.引言
近些年来,由于传染病在人口增长上的负面影响,了解这些疾病的动态行为并预测可能发生的情况是十分必要的.因此,建立数学模型研究传染病的动力学行为成为了帮助人们了解传染病传播模式和控制疾病的重要工具.在现实生活中,一些传染病在染病者康复后会赋予其暂时的或者永久的免疫力,对于其他一些疾病,康复的人可能会随着潜伏感染的重新激活而复发并恢复为染病者类,例如,牛结核病和人类疱疹,这类具有复发的疾病可以用SIRI(S-susceptible,I-infective,R-removed)传染病模型来进行描述[1−3].
设S,I,R分别表示易感者,染病者和康复者的人口密度,文[4]提出了一类具有复发的SIRI传染病模型:

其中Λ是易感人群的补充率,µ是人口的自然死亡率,β是疾病的传播系数,α是因病死亡率,κ表示了染病个体转化为康复个体的速率,γ表示了康复个体因复发而成为染病个体的速率,所有参数均为正数.
然而,由于不可预测的个体接触,传染病的发展和传播是不断变化着的.因此,研究环境噪声对于传染病的影响是十分必要的[5−9].结合文[4,6],本文研究了一类具有复发和饱和发生率的随机SIRI传染病模型:

其中λ表示染病个体转化为康复个体的速率,为饱和发生率,B(t)是标准布朗运动,σ表示白噪声的强度,其余参数与模型(1.1)相同,且所有参数均为正数.易得

则
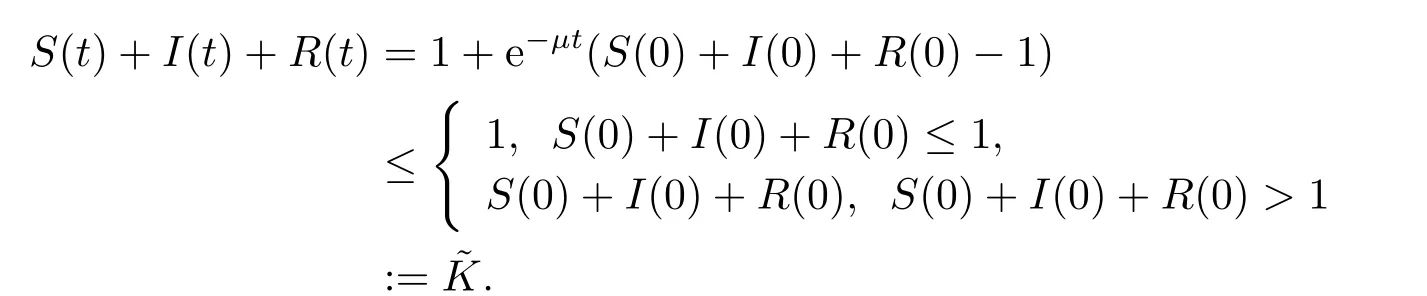
因此
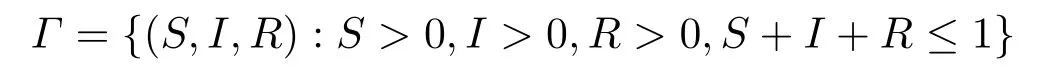
是系统(1.2)的正向不变集.假设(S(0),I(0),R(0))∈Γ,且S+I+R=1,(Ω,F,{Ft}t≥0,P)是一个完备概率空间,σ-代数族{Ft}t≥0满足非降和右连续,并且B(t)是定义在完备概率空间(Ω,F,{Ft}t≥0,P)上的布朗运动,Rn+={x ∈Rn:xi>0,1≤i ≤n}.
2.系统正解的存在与唯一性
为了研究系统的动力学行为,首先应该证明系统在任何初值下是否存在一个唯一的全局解(也就是说,在有限时间内未出现爆破).众所周知,为了保证随机微分方程存在唯一全局解,系统的系数通常被要求满足线性增长条件和局部Lipschitz条件[10].然而系统(1.2)的系数并不满足线性增长条件,但是满足局部Lipschitz条件,因此系统(1.2)的解可能会在某个有限时间点发生爆破.本节中,根据文[11]中的方法,我们给出如下定理.
定理2.1对于任意(S(0),I(0),R(0))∈Γ,当t ≥0时,系统(1.2)存在唯一正解并且它的解将依概率1停留在Γ内,即当t ≥0时,(S(t),I(t),R(t))∈Γa.s.
证因为系统(1.2)的系数满足局部Lipschitz连续条件,则对于任意给定初值(S(0),I(0),R(0))∈Γ,在t ∈[0,τe)内存在一个唯一局部正解(S(t),I(t),R(t)),其中τe为爆破时间[10].为了证明解是全局解,仅需证明τe=∞a.s.设k0≥1足够大,使得S(0),I(0),R(0)均位于区间[1/k0,k0]内.对于每一个整数k ≥k0,定义停止时间
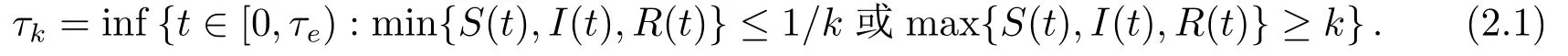
设inf ∅=∞(其中∅表示空集).因此,当k →∞时,τk单调递增.设τ∞=limk→∞τk,显然τ∞≤τea.s.如果τ∞=∞a.s.则τe=∞a.s.并且当t ≥0时,(S(t),I(t),R(t))∈Γa.s.因此,要证明定理成立,仅需证τ∞=∞a.s.设τ∞=∞a.s.不成立,则存在一对常数T >0和ε ∈(0,1)使得P{τ∞≤T} > ε,因此存在整数k1≥k0使得P{τk≤T} ≥ε对于任意k ≥k1成立.
定义C2-函数V1:Γ →R+如下:
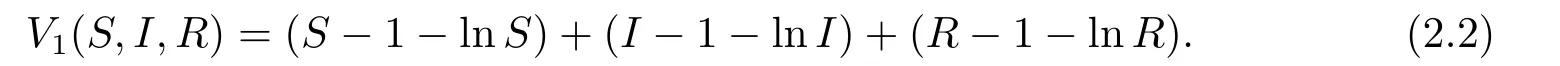
显然函数V1(S,I,R)≥0恒成立.根据Itˆo公式可得
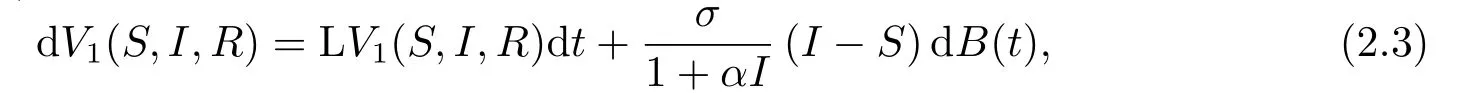
其中
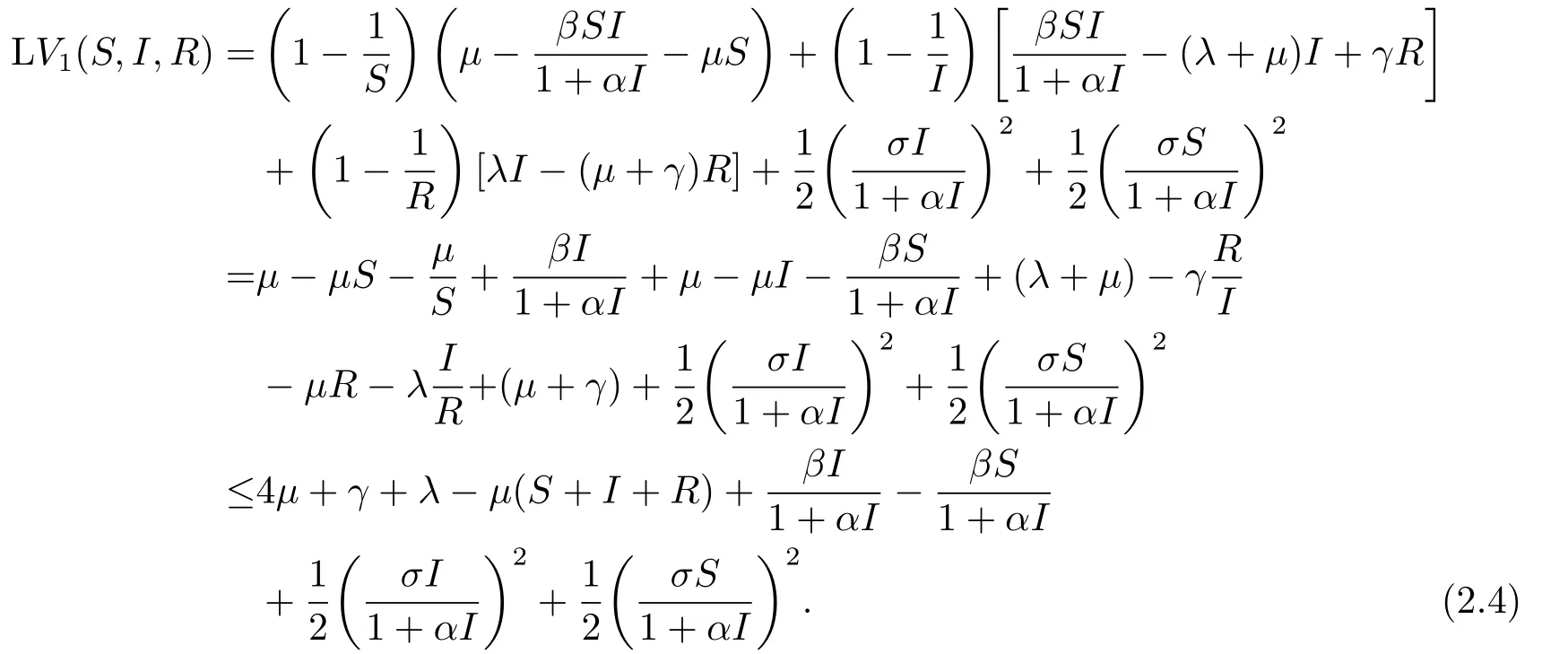
由Γ的定义可得,
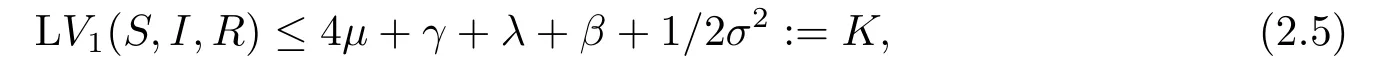
其中K是正常数.则

对(2.5)式两边同时从0到τk∧T=min{τk,T}积分,然后取期望可得
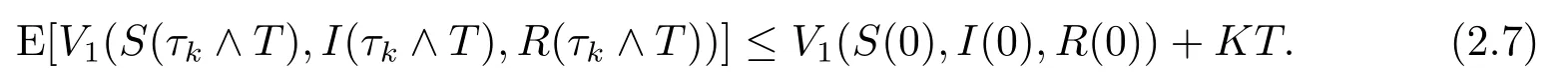
设Ωk={τk≤T},k ≥k1,根据(2.1)可得,P(Ωk)≥ε.注意到对于任意ω ∈Ωk,S(τk,ω),I(τk,ω)和R(τk,ω)中至少有一个等于k或1/k.因此V1(S(τk,ω),I(τk,ω),R(τk,ω))不小于
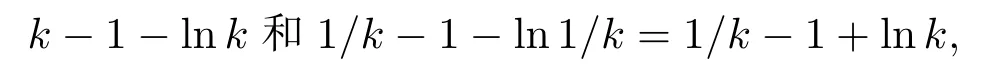
则V1(S(τk,ω),I(τk,ω),R(τk,ω))≥(k −1−lnk)∧(1/k −1+lnk).由(2.7)式可得

其中IΩk表示Ωk的示性函数.令k →∞,则∞≥V1(S(0),I(0),R(0))+KT=∞,显然存在矛盾.因此必有τ∞=∞a.s.这意味着解(S(t),I(t),R(t))依概率1在有限时间内不会发生爆破.证毕.
3.疾病的灭绝性
本节中,通过构建适当的Lyapunov函数,我们得到了疾病灭绝的充分条件.
定理3.1对于任意(S(0),I(0),R(0))∈Γ,若则无病平衡点E0依概率全局渐近稳定.
证定义Lyapunov函数
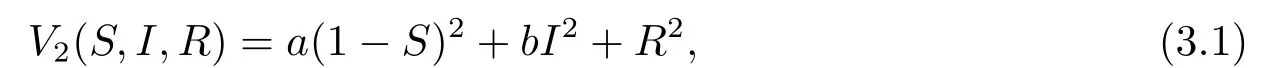
其中a,b是正实常数.根据公式可得
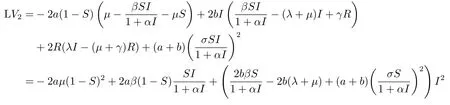

因为S,I ∈(0,1),则

又因为
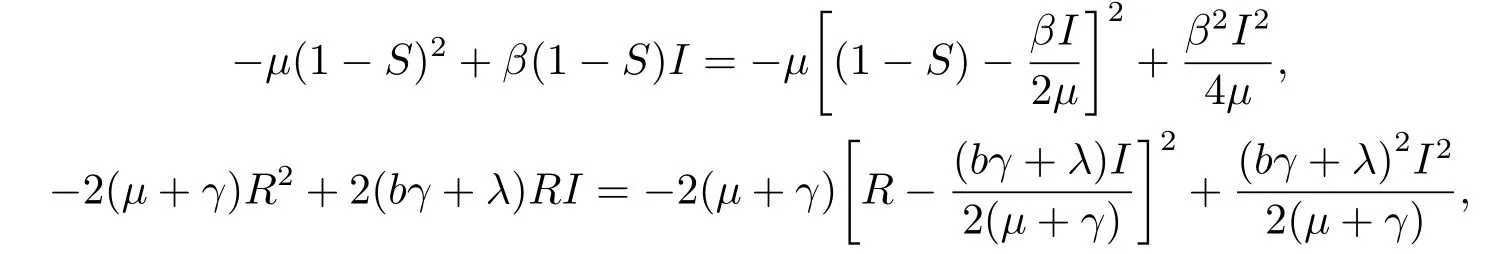
则由(3.3)式可得

其中
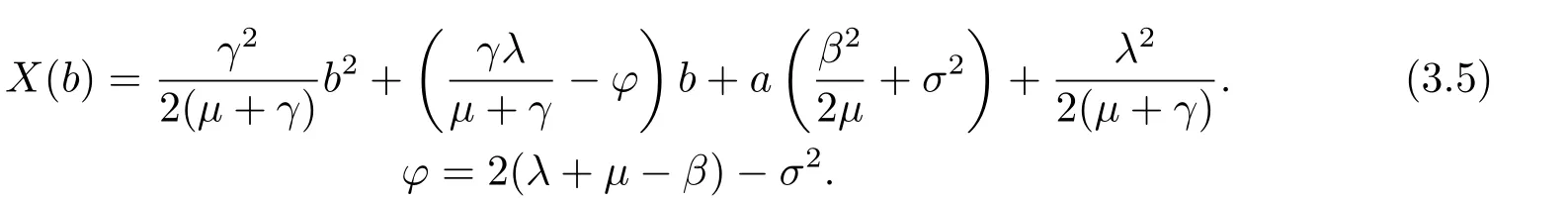
注意到,当X(b)<0时,LV2负定.由(3.5)式可得
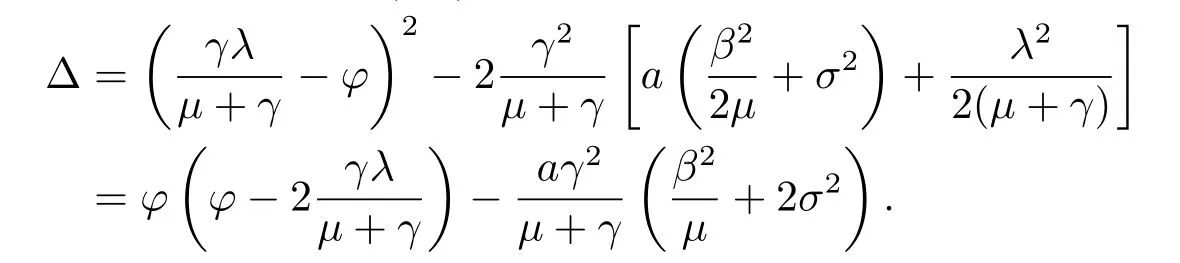
当φ −2γλ/(µ+γ)>0且a足够小时,∆>0成立,则函数X(b)存在两个正根b1和b2.因此,对于任何b ∈[b1,b2]有X(b)<0.将φ=2(λ+µ−β)−σ2代入不等式φ −2γλ/(µ+γ)>0可得
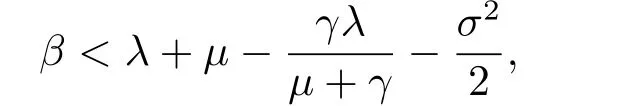
因此,LV2负定,无病平衡点E0依概率全局渐近稳定.证毕.
定理3.2对于任意(S(0),I(0),R(0))∈Γ,若则(I(t),R(t))指数收敛于(0,0) a.s.
证设θ为一正常数.根据Itˆo公式可得

由定理2.1可得
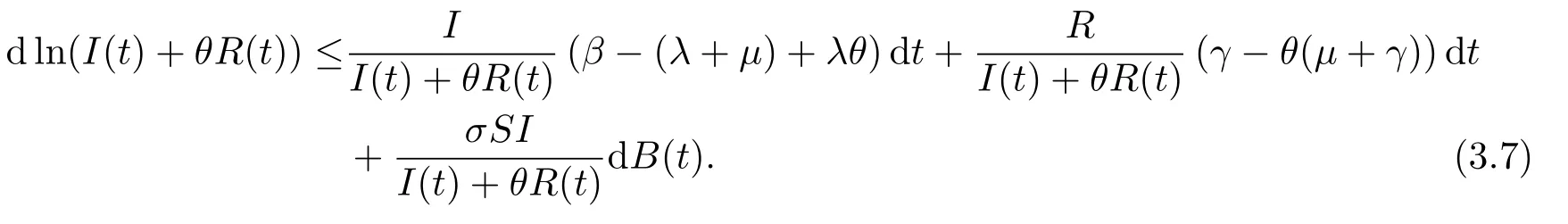

由(3.8)式可得,存在m >0使得γ −θ(µ+γ)< −mθ成立.因此有µ+λ −β成立.则m取值范围如下

设n=max{β −(λ+µ)+λθ,−m}<0,因此
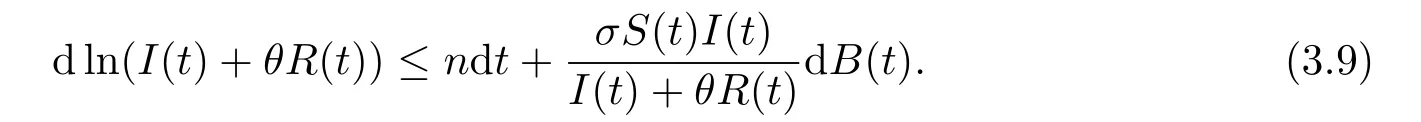
对(3.9)式两边从0到t积分,可得

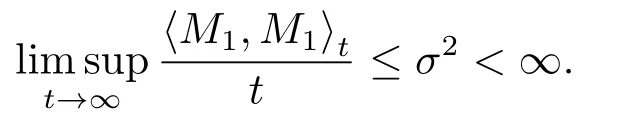
因此,由大数定理得

则结合(3.10)和(3.11)式可得
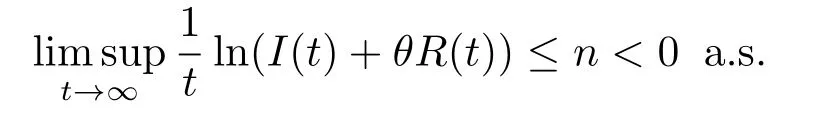
证毕.
4.疾病的持久性
本节,我们研究了疾病的持久性.
定理4.1对于任意(S(0),I(0),R(0))∈Γ,若R0>1,则系统的解满足
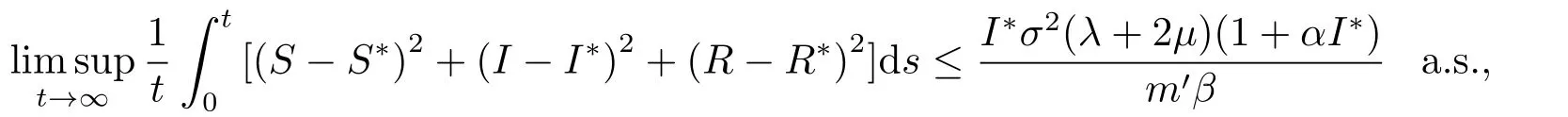
其中m′=min(2µ,2γ),E∗=(S∗,I∗,R∗)为非随机系统的地方病平衡点.
证设x,y为正常数,定义函数
其中
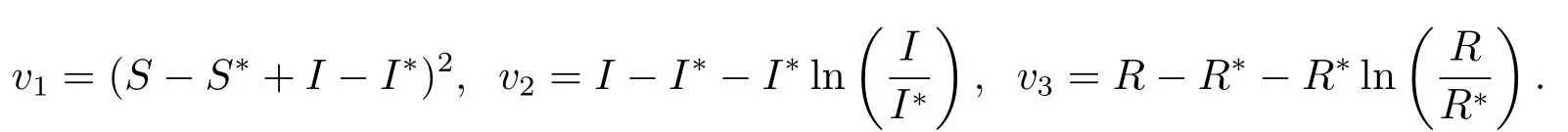
根据Itˆo公式可得

计算可得
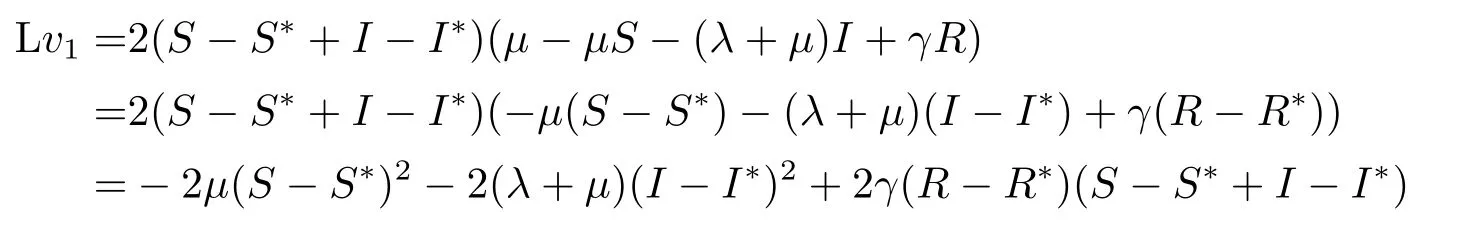

因为S+I+R=S∗+I∗+R∗=1,则
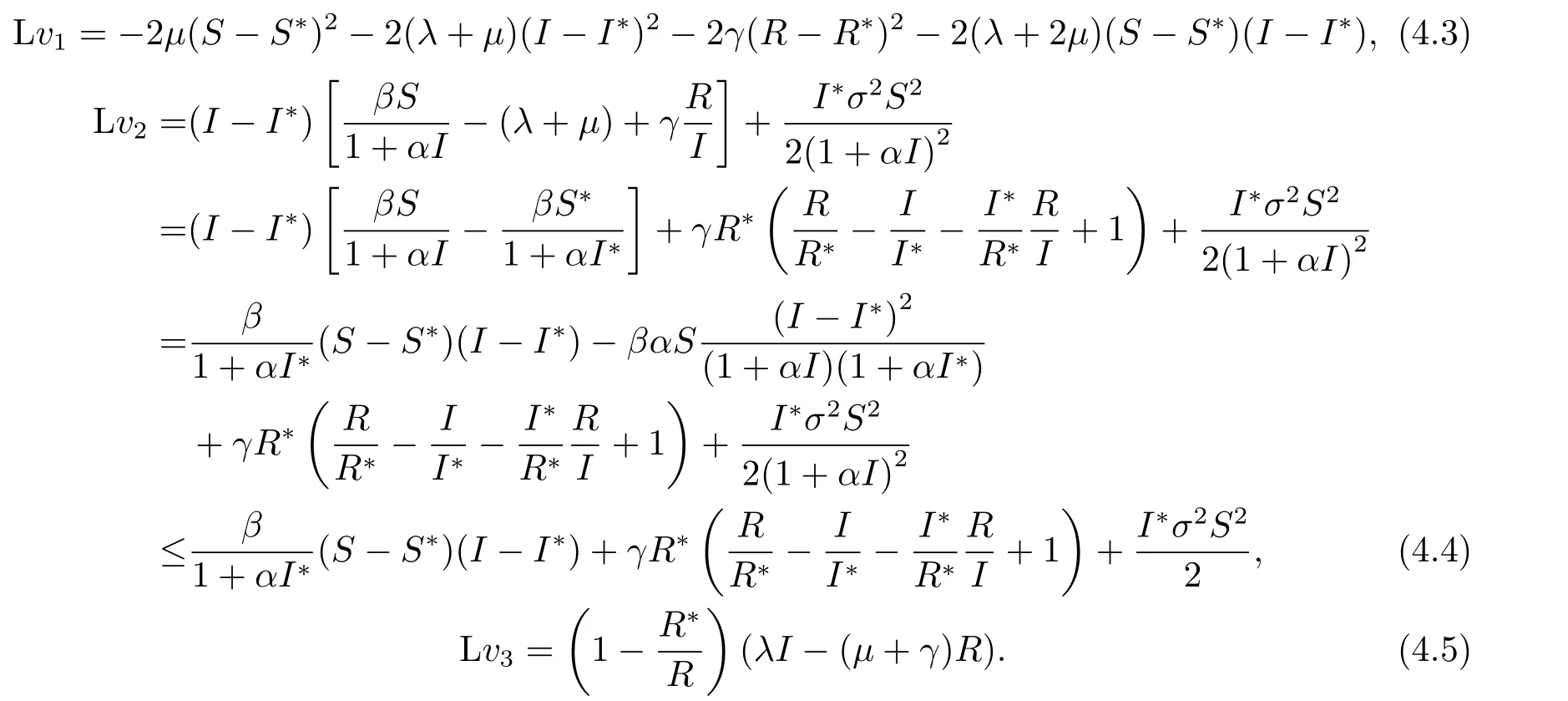
又因为λI∗−(µ+γ)R∗=0,则
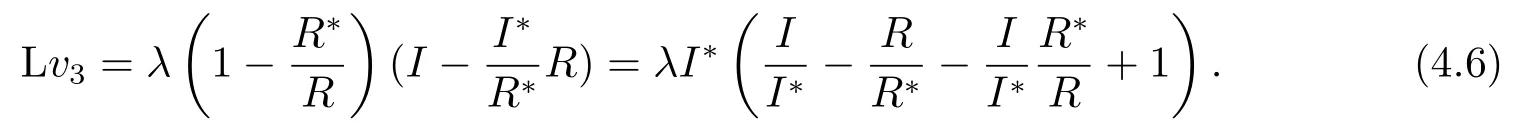

取m′=min(2µ,2γ),则
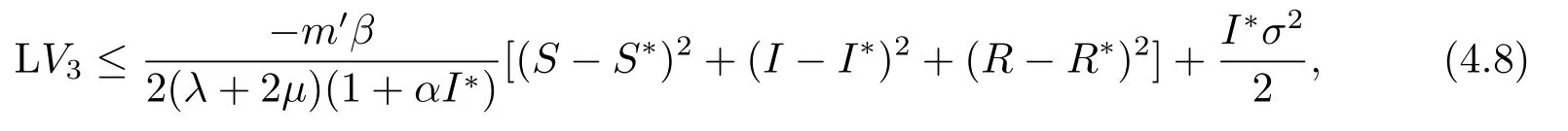
因此

对(4.9)式两边从0到t积分,可得

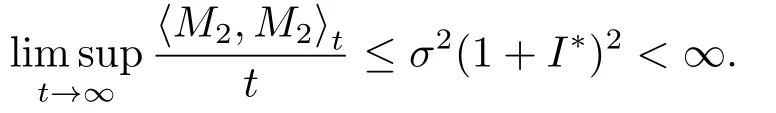
因此,由大数定理得
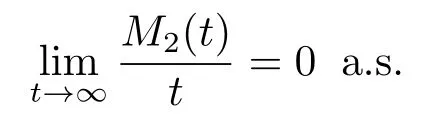
所以
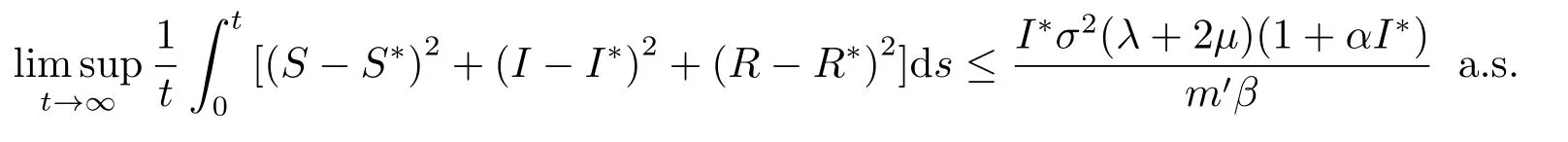
证毕.
定理4.2设(S(t),I(t),R(t))是系统(1.2)对于任意初值(S(0),I(0),R(0))∈Γ的解,若Rs=成立,则疾病将持续存在,即,
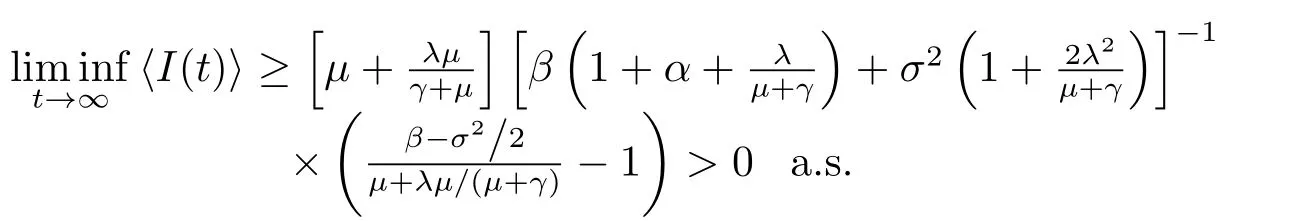
证对系统(1.2)积分,可得S(t)+I(t)+R(t)=1+e−µt(S(0)+I(0)+R(0)−1),和综合上式,可得

其中
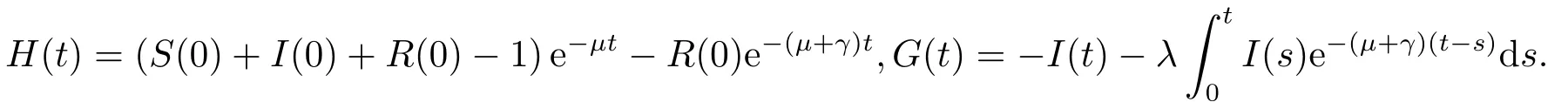
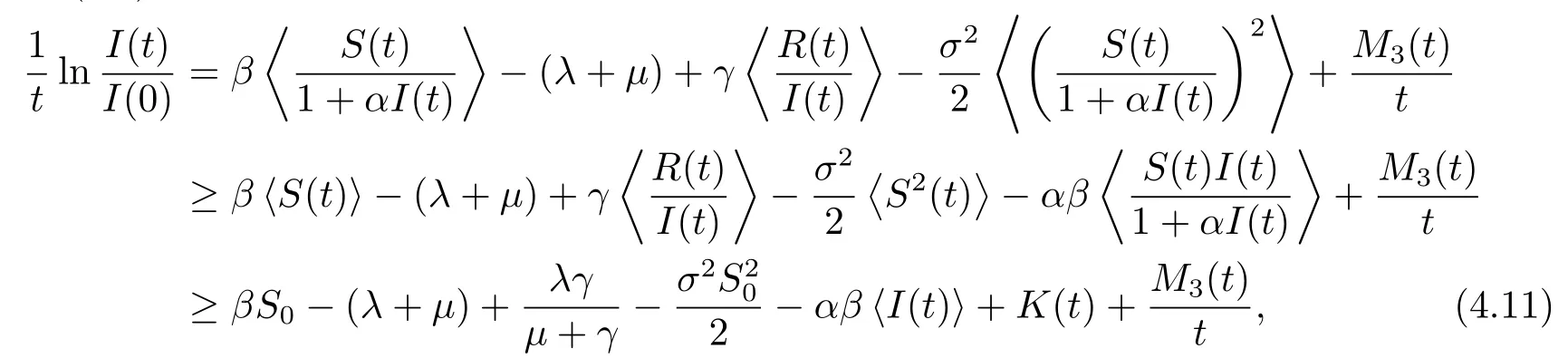
其中
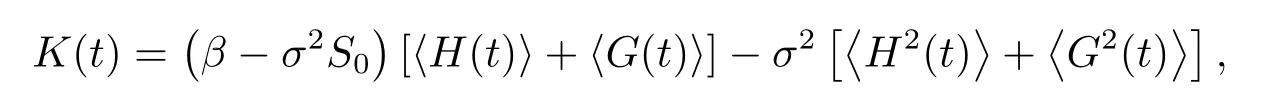
计算可得
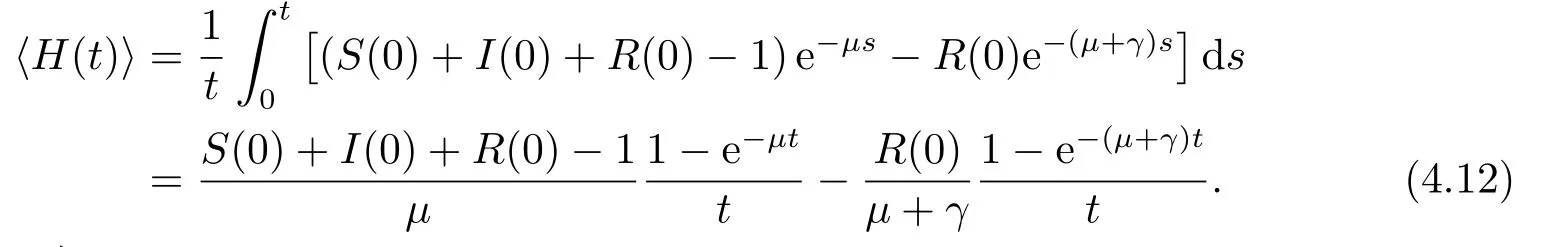
显然,当t →∞时
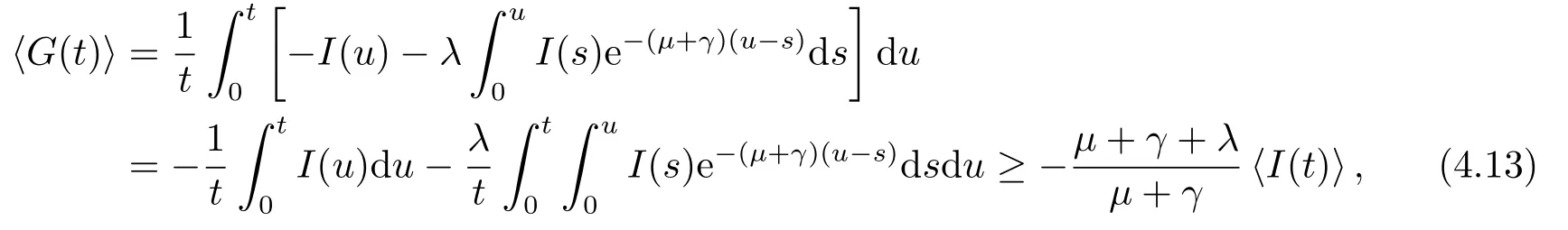
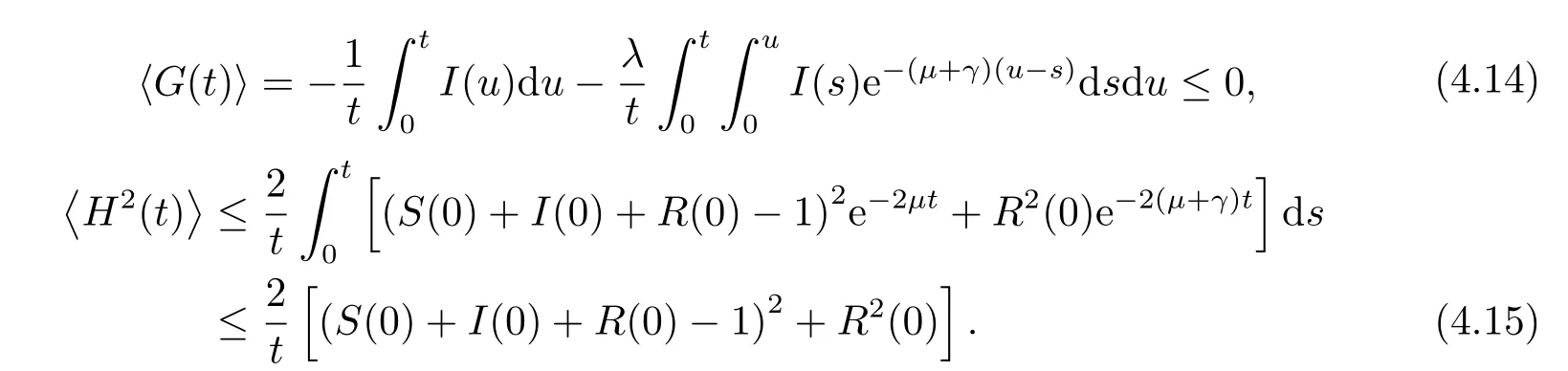
显然,当t →∞时
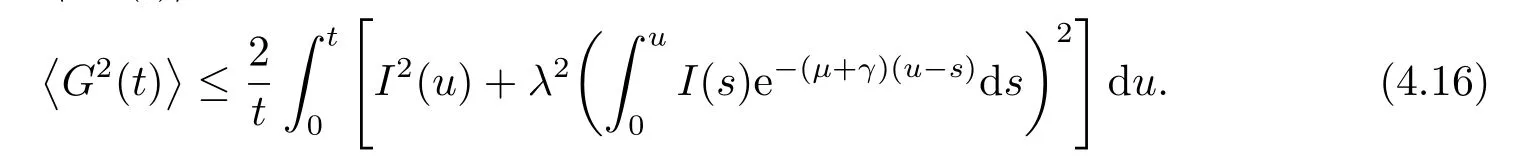
将I放大至1,则

综合上式并结合文[12]中引理5.2,可得
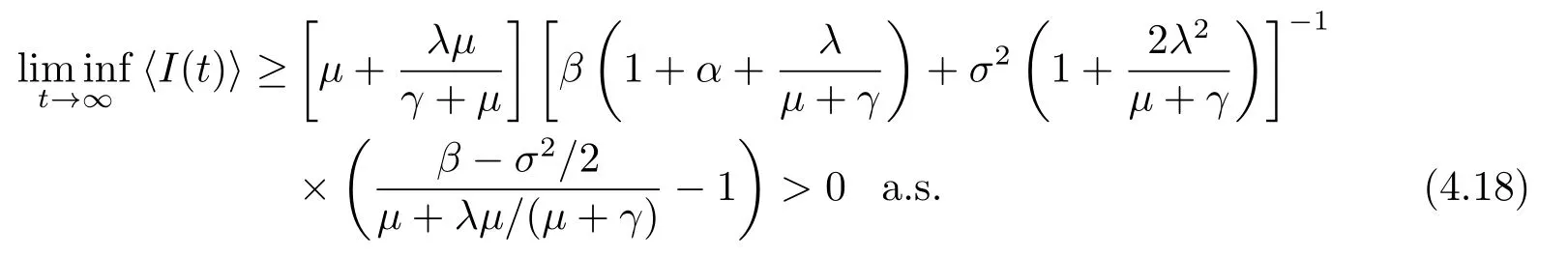
证毕.
5.数值模拟
本节我们应用文[13]中提出的Milstein高阶方法对系统(1.2)的解进行数值模拟,参数根据参考文[6]选取,部分数值如下表所示

表5.1 数值模拟中参数和初值取值
图中Stochastic表示随机系统曲线,Deterministic表示非随机系统曲线.
图5.1中,选取参数σ=0.4,γ=0.012,使得数值模拟验证了定理3.1的结论,此时疾病将会灭绝.
图5.2,5.3中,选取参数γ=0.03,计算可得R0=0.875<1,数值模拟验证了定理3.2的结论,此时系统的无病稳态将吸引系统(1.2)的所有正解,并且随着σ的增大,灭绝的速率也会增大,因此白噪声会加速疾病的灭绝.
图5.4中,选取参数σ=0.2,γ=0.1,计算可得Rs=1.2394>1,数值模拟验证了定理4.1,4.2的结论,其中随机系统的解在地方病平衡点E∗周围持续性地周期振荡,此时疾病将会持续存在.

图5.1 σ=0.4,γ=0.012
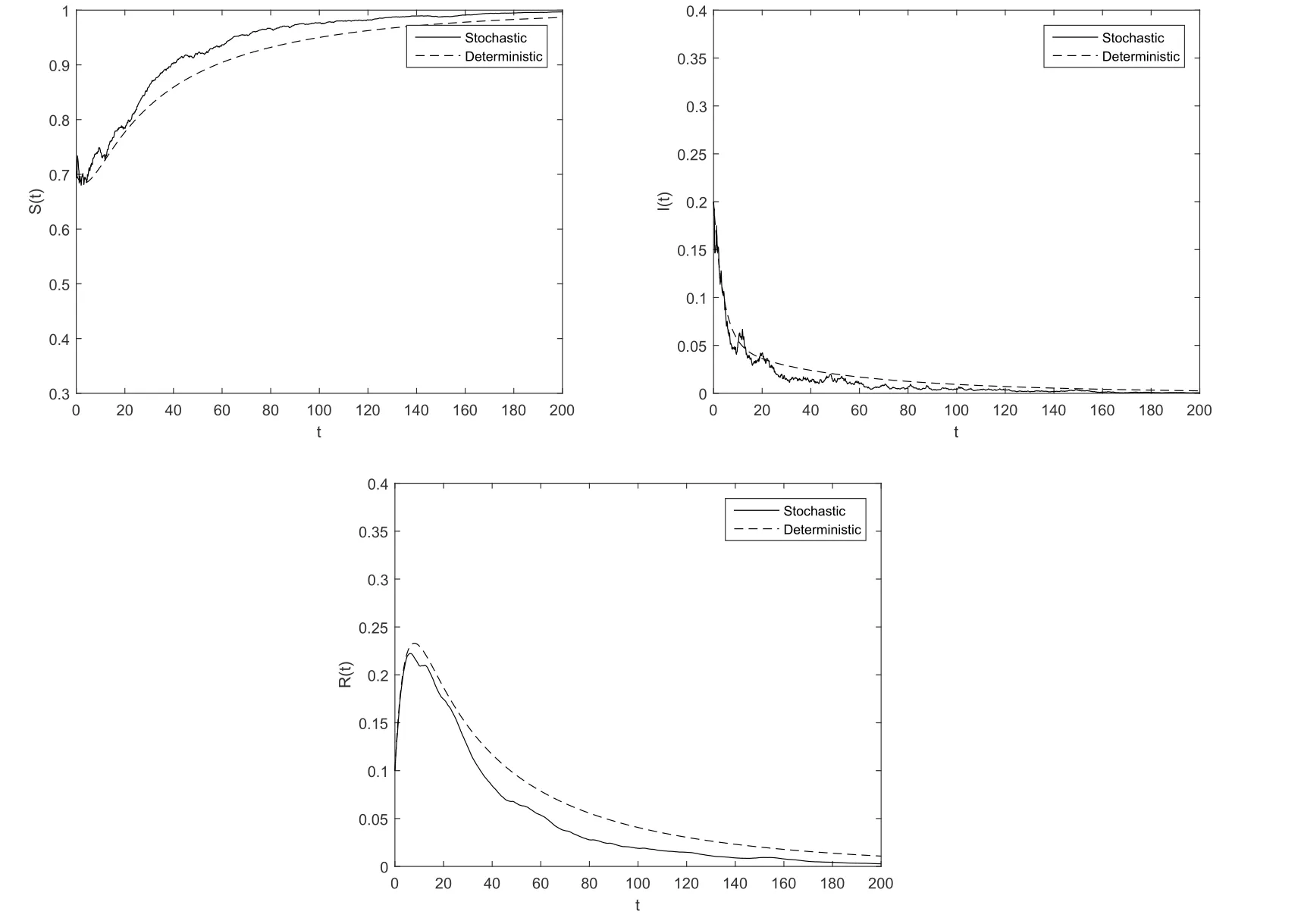
图5.2 σ=0.2,γ=0.03
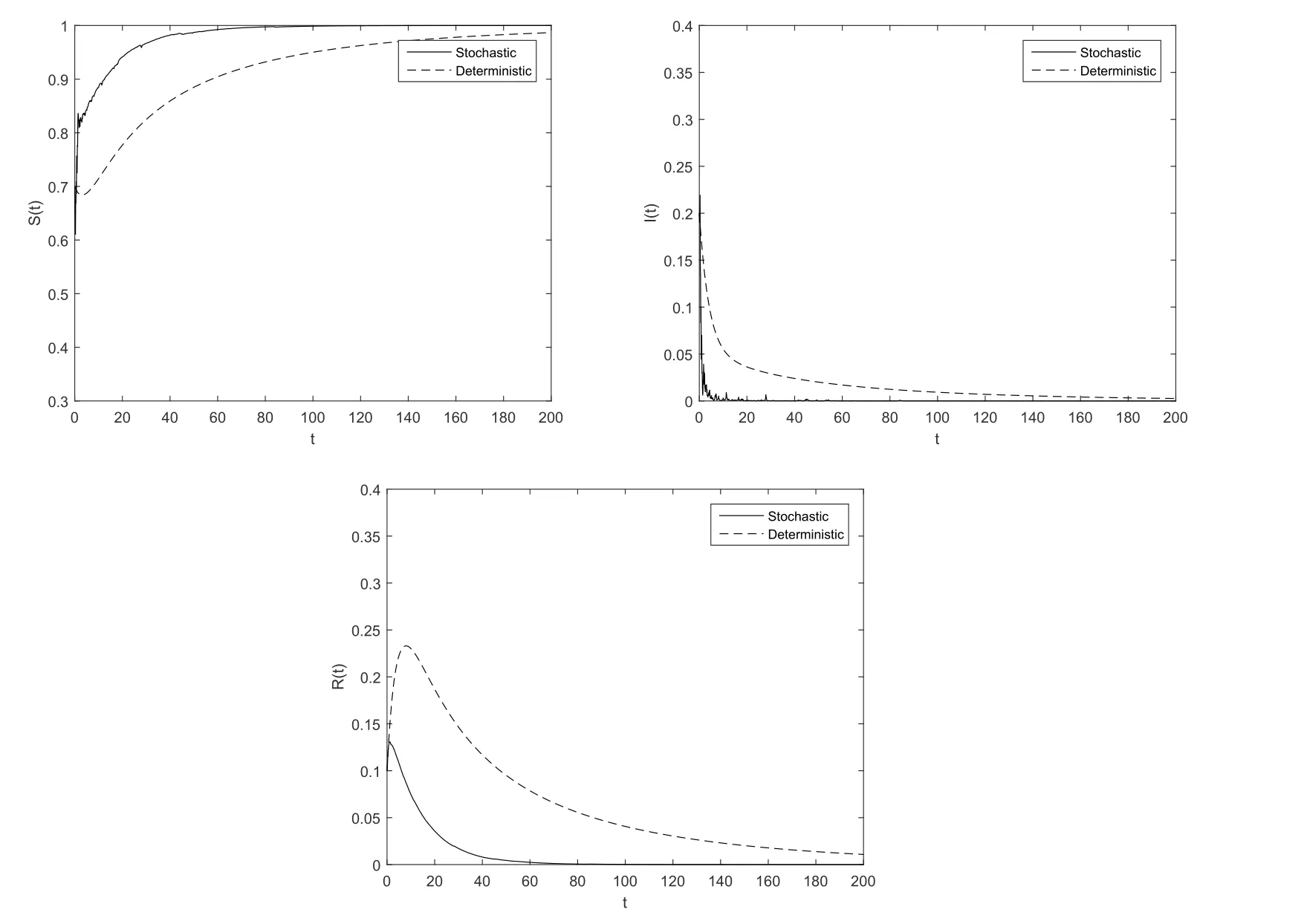
图5.3 σ=2,γ=0.03
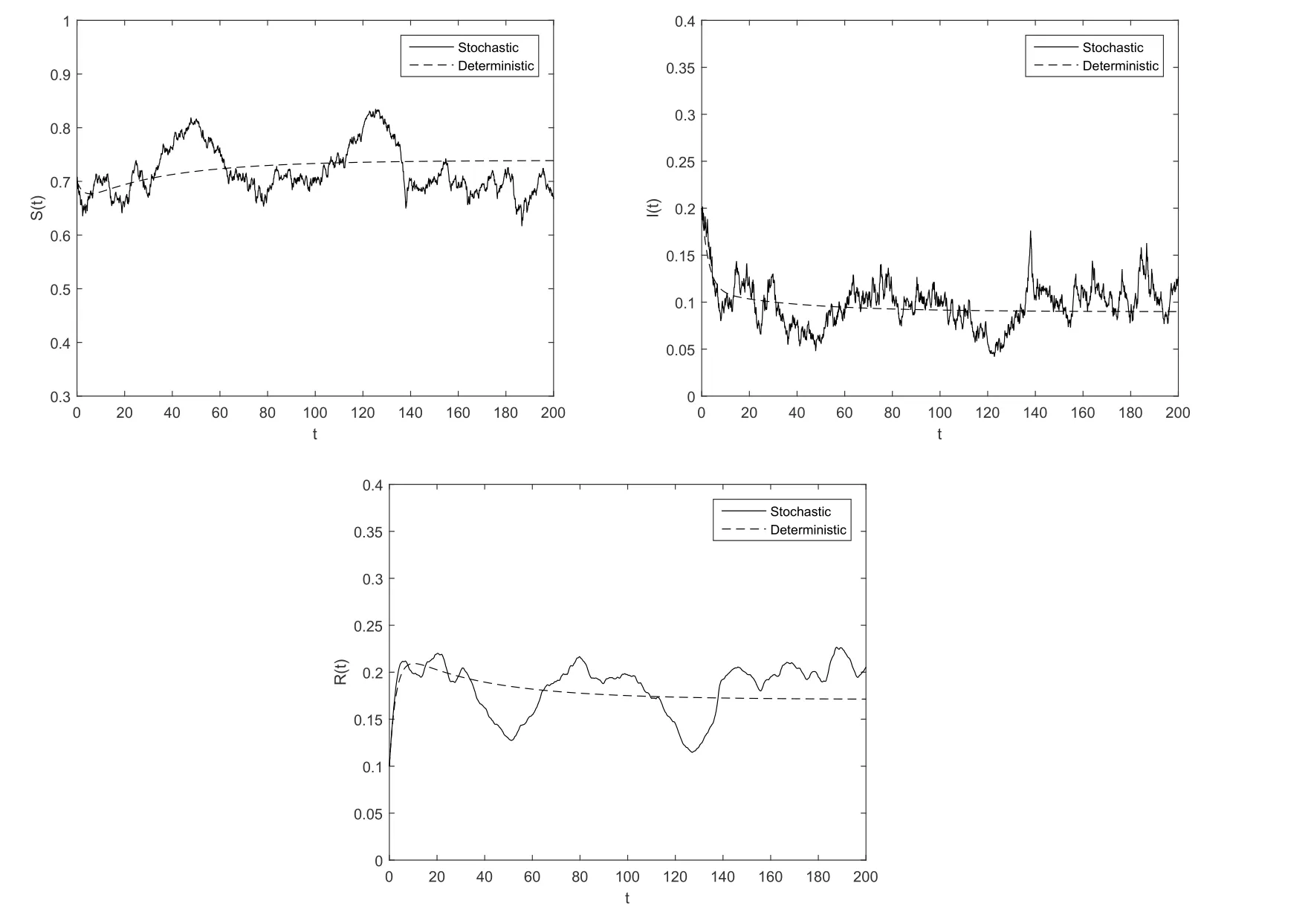
图5.4 σ=0.2,γ=0.1
