V锥节流装置内气液分层流动特性数值模拟
2019-06-27贺登辉陈森林白博峰
贺登辉, 陈森林, 白博峰
(1.西安理工大学省部共建西北旱区生态水利国家重点实验室,陕西西安 710048;2.西安交通大学动力工程多相流国家重点实验室,陕西西安 710049)
气液分层流是湿气多相流(湿天然气、湿蒸汽等)中的一种重要的流动形态,广泛存在于工农业生产过程中。气液分层流的测量非常重要。目前虽然有许多种方法可以测量气液分层流流量,但应用最多的仍然是差压法[1-2]。作为一种新型的差压式流量计,V锥流量计因其具有信号稳定、压损低、量程比宽、所需直管段短等优点[3-7],近年来在多相流测量领域受到了越来越多关注。对V锥流量计测量湿气时的差压响应特性研究表明, V锥流量计湿气测量特性主要受气、液相含量、压力及节流比等因素影响[3, 7-11]。Stewart等[8]采用Steven文丘里关联式[10]的建立方法,得到对不同节流比V锥流量计的测量关联式;Steven等[3,12]对管径为101.6和152.4 mm,节流比为0.75的V锥流量计,改进了de Leeuw关联式测量模型;徐英等[13]通过对V锥流量计测量湿气时产生的“过读”进行修正,建立了一套湿气测量模型;爱默生公司[14]基于V锥流量计,开发了Roxar湿气流量计,并成功应用于实际油气井气液流量测量中,但该公司未公布其V锥流量计具体采用何种修正模型。由于V锥流量计在湿气测量时比文丘里管对液相测量精度的依赖更低[9,15],这对于提高其气相测量精度十分有利。目前对于V锥流量计关注的重点多是不同结构参数及流动参数下V锥流量计的差压响应特性,但V锥节流装置内的气液两相流动特性及其对差压测量的影响机制知之较少。笔者针对实际湿气中常见的气液分层流采用数值模拟方法对V锥节流装置内气液分层流动特性进行研究。
1 数值模拟方法及模型
1.1 数值模拟方案
V锥节流元件的结构如图1所示。节流元件由前、后锥角分别为φ和θ的两个V形锥体组成,并且由支撑杆固定在管道上;高压取压口位于V锥元件上游,低压取压口位于后锥体的顶点处,穿过锥体由支撑杆引出管外。管道内径为50 mm,V锥的节流比为0.55,前、后锥角分别为45°和135°。
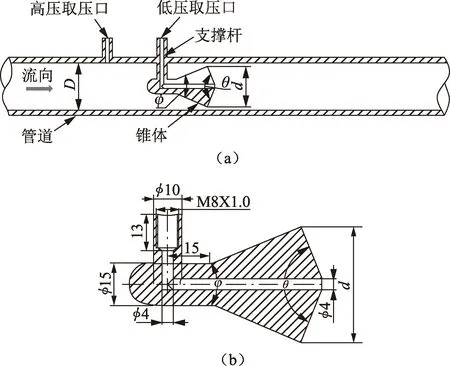
图1 V锥节流装置Fig.1 V-Cone throttle device and structure
基于ANSYS Fluent平台,对空气、水流经V锥节流装置的流动特性进行数值模拟。由于来流是分层流,主要包括光滑分层流、波状分层流及滚动波状流,不考虑分层流内液滴的运动,采用VOF模型捕捉气液界面[16]。如图2(a)所示,所模拟的V锥装置上、下游直管段分别为5D和9D,这与试验中的测压点布置保持一致。采用速度入口边界条件,分为两部分,其中气相由中间的圆形区域进入管道,液相由环形区域进入。对于本文中研究工况,气液两相经过5D的长度,在进入V锥节流段时可达到气液分层流态;出口采用压力出口边界条件,壁面无滑移;模拟的工况进出口边界条件均为试验值。湍流模型采用RNGk-ε模型[17];采用结构化六面体网格对模拟区域进行划分,并在锥体附近进行网格加密处理(图2(b))。
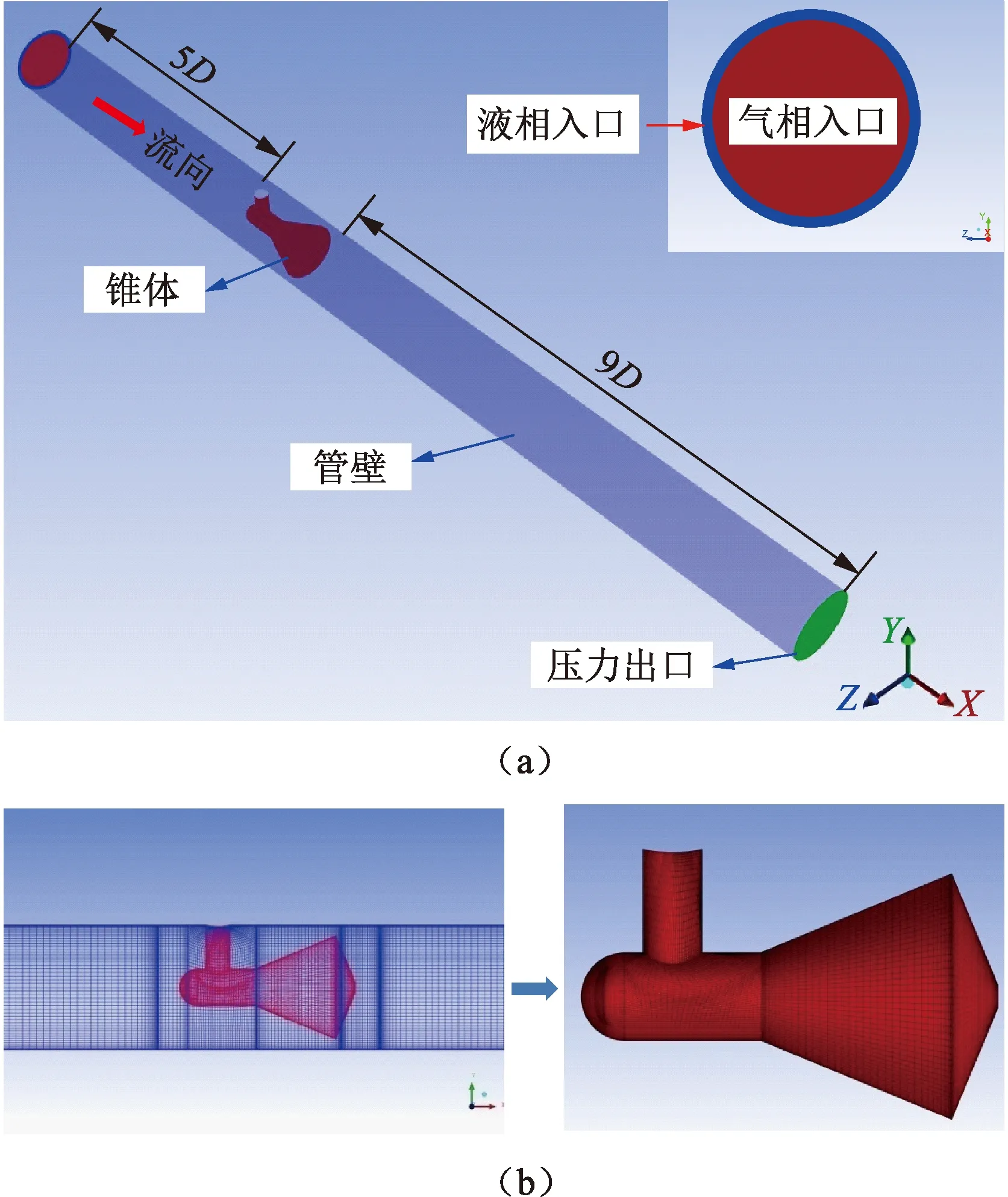
图2 几何模型及网格划分Fig.2 Geometry model and mesh
1.2 数学模型
由于涉及的数学模型众多,仅对几个主要的模型进行介绍,其他模型可以参考ANSYS Fluent帮助文献[18]。
1.2.1 连续性方程
采用VOF模型模拟气、液两相流时,两相流体使用同一个方程组,每一相的体积分数在整个计算域内被追踪。通过求解其中一相体积分数的连续方程来跟踪气、液两相之间的界面。第q相的连续性方程为
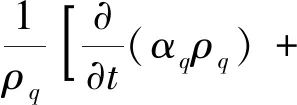
(1)
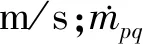
由于不考虑相变,传质及源项均取为零。
气、液两相的体积分数之和满足
αg+αl=1.
(2)
连续性方程采用隐式时间离散格式进行求解,单元内的物性参数根据气、液两相体积分数加权平均得到。气、液混合物的平均密度ρ和黏度μ分别为
ρ=αgρg+(1-αg)ρl,
(3)
μ=αgμg+(1-αg)μl.
(4)
式中,μg和μl分别为气相和液相的动力黏度,Pa·s。
1.2.2 动量方程
动量方程通过气、液混合密度ρ和动力黏度μ与体积分数相联系,在整个计算区域内求解同一动量方程,得到的速度场也被两相共同使用。动量方程为
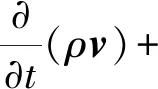
ρg+Fvol.
(5)
其中
式中,p为压力,Pa;Fvol为作用于气、液间相界面的体积力,N/m3;κg为曲率,1/m。
1.2.3 能量方程
由于V锥节流的影响,流体温度在锥体附近可能会发生变化,因此,考虑了温度对能量传递的影响。气液两相共用能量方程为

(6)
式中,keff为有效热导率,由气液两相共用,W/(m·K);T为温度,K;E为能量,J。
VOF模型中取两相质量加权平均值计算能量及温度,对于能量有
(7)
式中,Eq为按单相比热容和共用的温度计算的每一项能量,J。
1.3 模型验证
1.3.1 网格独立性验证
采用3组不同的网格数进行网格无关性验证(图3,其中Usg为表观气速,m/s;Usl为表观液速,m/s),网格单元数依次增大约1.5倍,如表1所示。由图3可知,网格2与网格3计算结果相比,沿流动方向(X轴方向)的静压力分布变化很小,可认为网格2能够满足计算需求。
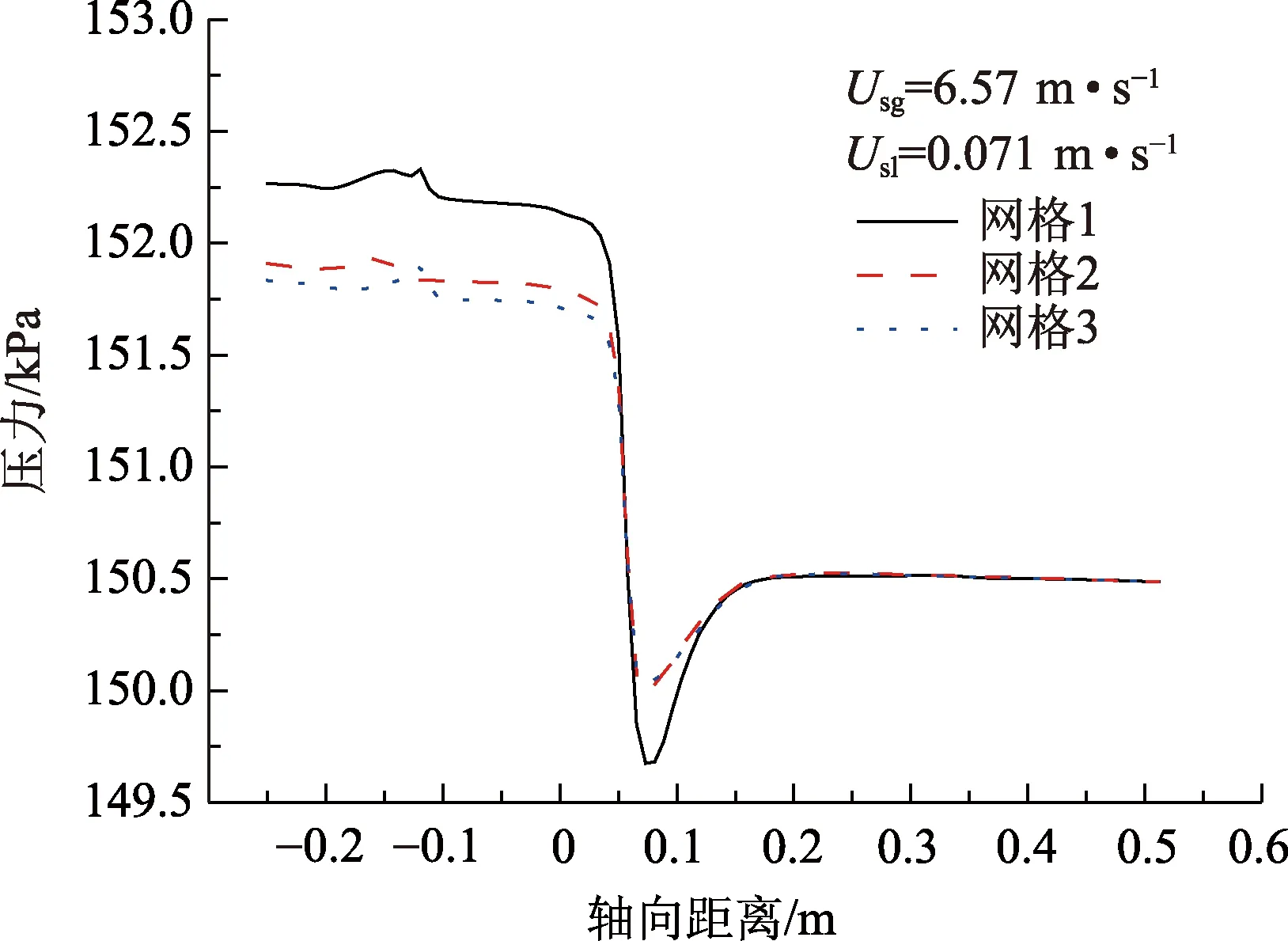
图3 网格数量变化时压力模拟结果对比Fig.3 Wall pressure profiles under different meshes

网格节点数单元数 网格1963199936360 网格214879811452880网格322140012168992
1.3.2 试验数据验证
采用网格2方案进行模拟,得到沿流动方向静压力分布,与试验结果(试验装置和方法见参考文献[4])进行对比 (图4)。由图4可知,两者吻合良好,最大相对误差小于5.0%,表明所建立的数值方法可靠,能够反映出气液两相流在V锥节流装置内的压力分布特性。
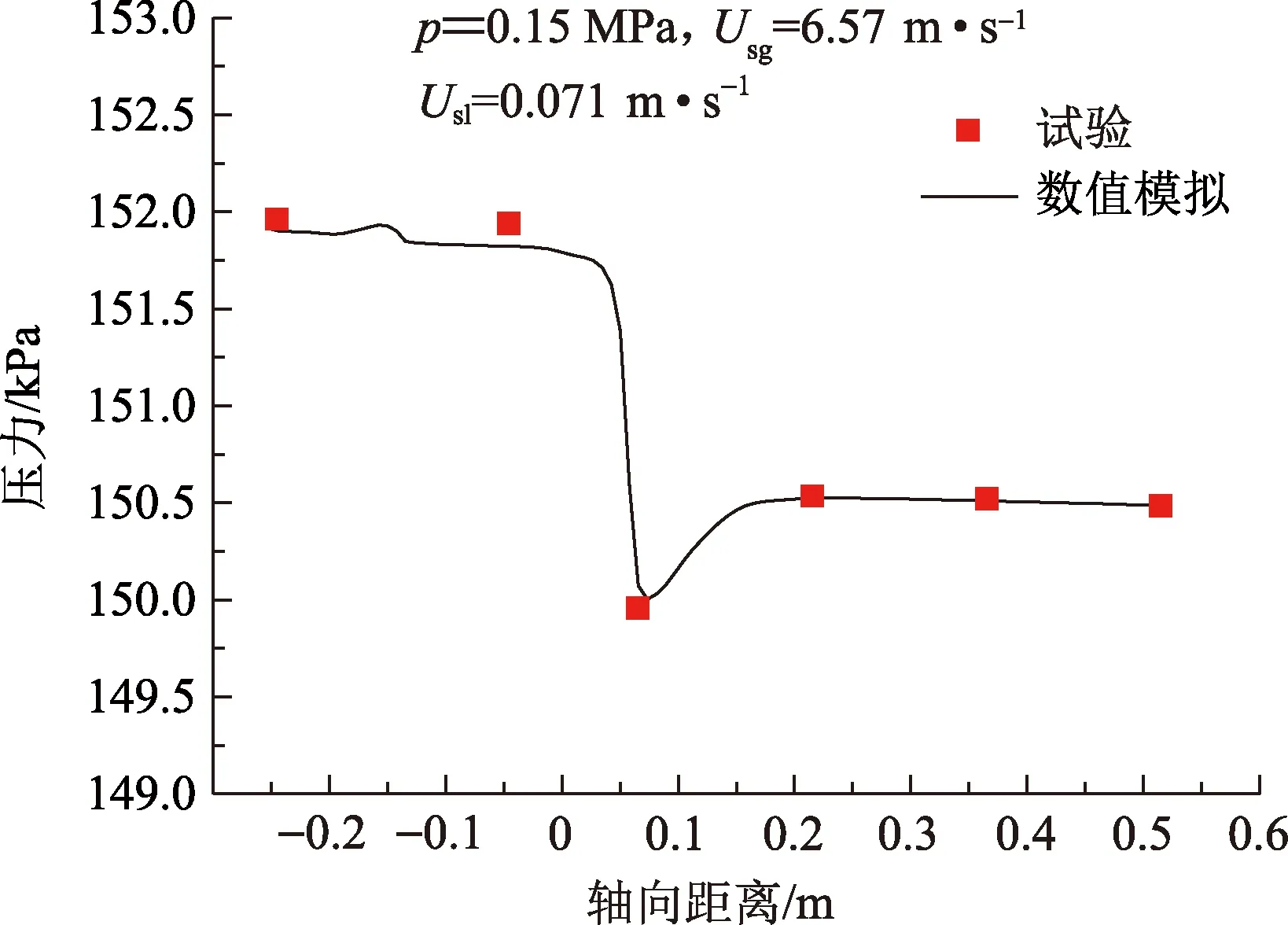
图4 数值模拟与试验得到的沿流动方向静压对比Fig.4 Comparison of wall pressure profile between numerical simulation and experimental results
2 数值结果分析
2.1 锥尾尾涡特性
2.1.1 尾涡基本特征
当来流为单相气体时,如图5(p=0.2 MPa,Usg=5.71 m·s-1,Usl=0)所示,单相气体流经V锥,在喉部形成环形射流,射流撞击壁面,发生反弹,并在喉部下游一定距离处射流速度达到最大;在射流剪切作用下,V锥锥尾区域压力梯度变化较大,锥尾下游出现了尾流,形成了尾流漩涡(尾涡),尾涡涡心速度较低。流动速度在尾涡下游端点附近达到最小,沿流动方向速度接近于0处的位置即为尾涡的下游端点。尾涡尺度较大,长度Lvortex约为锥体直径d的2~3倍;由于V锥节流装置边壁收缩,尾涡靠近管壁处的流动方向与主流相同,中心区的流动方向与主流相反(图5(b)和(c))。
当来流为气液分层流时,V锥下游尾涡特征呈现出上部大下部小的形态,靠近管道下壁面处的尾涡长度与单相气体中的相比,其长度大大缩短。例如,图6(p=0.2 MPa,Usg=5.71 m·s-1,Usl=0.057 m·s-1)工况中的尾涡长度与图5的工况相比,缩短了约40%。其主要影响机制为:①流体物性的影响。单相气体中加入液相后导致流体的混合密度和黏度等物性均发生变化,而密度增大幅度远远大于黏度,再加上喉部射流速度相对于单相气体急剧增大,从而导致流体雷诺数增大,加剧了气液动量交换,能量损失增大,尾涡长度缩短;②V锥喉部射流的影响。射流使气液撞击壁面,液体发生反弹和破碎,少量液体被卷吸进尾涡中,消耗了尾涡的能量。同时随液量增大,反弹的液体高度增大[4],从而阻碍了尾涡发展。

图5 单相气体条件下的流动Fig.5 Streamline and velocity vector distribution under single-phase gas flow

图6 气液两相流条件下的流动Fig.6 Streamline and velocity vector distribution under annular flow
尾涡形成和发展对沿流动方向的静压分布产生影响。图7为单相气体和气液两相流条件下壁面静压沿流动方向分布(p=0.2 MPa)。由图7可知,流体流经V锥,压力逐渐降低,在锥尾下游某处压力达到最低,之后逐渐恢复;其恢复长度受尾涡的影响,尾涡越长,则压力恢复所需的距离越长;随着尾涡影响的减弱,下游压力也逐渐恢复,经过一定长度的过渡区域,当流线与主流方向趋于平行时,流动即可恢复。图7中的气液两相流尾涡长度与单相气体中的基本相等,因此所需的压力恢复长度也相差不大。
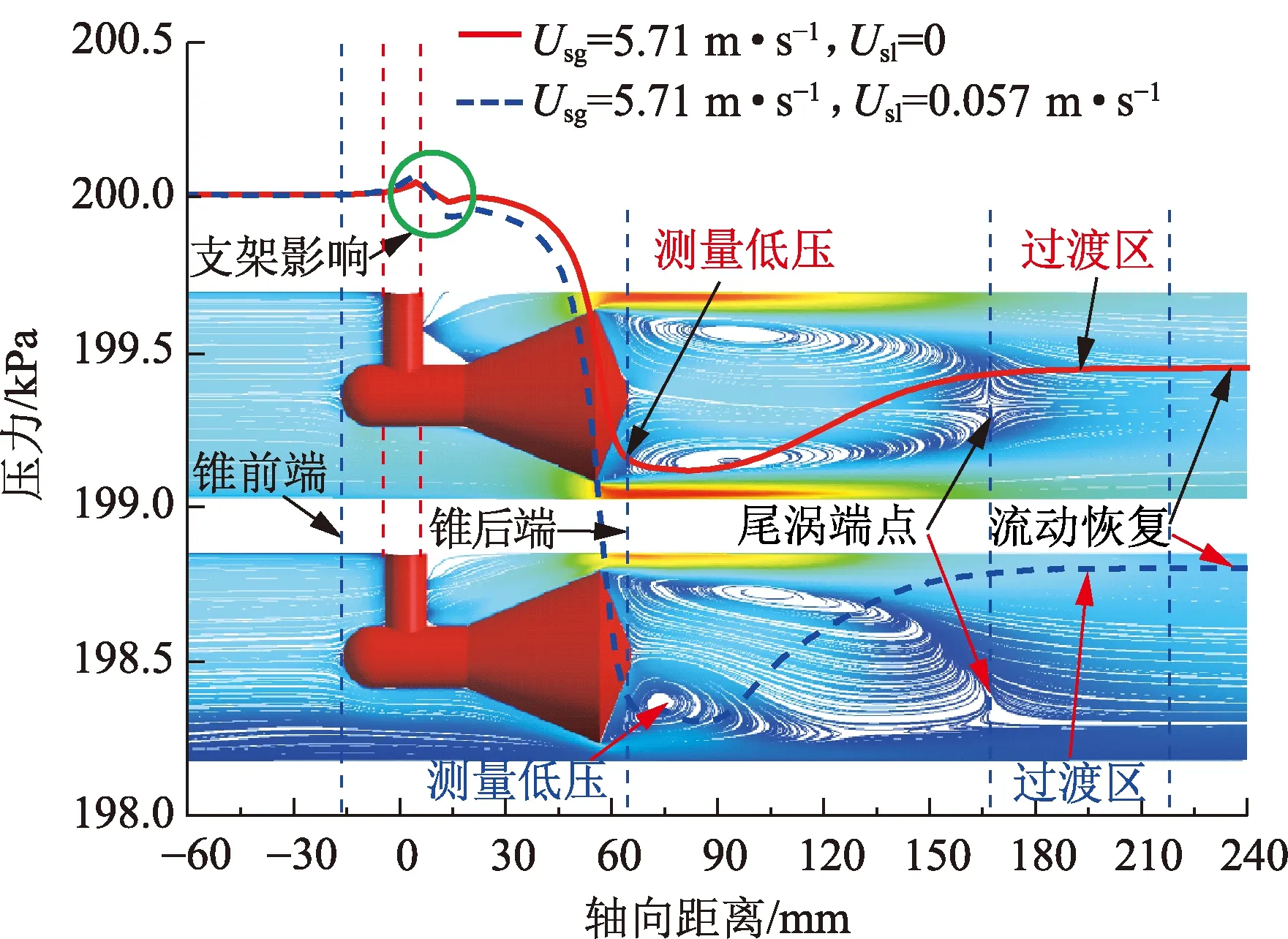
图7 流动对管壁静压的影响Fig.7 Effect of vortex on wall pressure
2.1.2 影响因素
单相气体中引入液相,使得锥后尾涡发生变化。图8为表观液速对尾涡的影响(刻度尺单位为mm,上图为XOY截面,下图为XOZ截面)。由于尾涡是立体的,为了更全面的认识尾涡,给出了其在XOY和XOZ两个截面上的分布。单相气体中,尾涡沿轴线基本对称(图8(a));加入液相后,尾涡开始呈现上部大下部小的形态,且随着表观液速增加,尾涡长度发生变化,且尾涡下游端点越来越向管道下部倾斜。这意味着管道上部流场的稳定区域增大,尾涡对下游的影响也减弱。尾涡形状的变化主要是由于分层流来流时,液相主要分布在管道下部,因此下部流速较低,V锥喉部射流作用较弱,导致了尾涡向管道下部倾斜,而XOZ截面上尾涡分布的对称性基本不受表观液速影响。此外,气、液表观流速基本相同的情况下,尾涡基本不受来流入口压力的影响。在本文气液分层流范围内,流体温度变化较小(小于1 ℃),因此温度对测量的影响亦较小。

图8 液相对尾流漩涡的影响Fig.8 Effect of liquid velocity on vortex
2.1.3 尾涡对下游流动影响
尾涡影响下游流体速度及压力分布特性。图9为来流经过V锥之后,上下游截面速度沿Y轴方向分布,其中0D表示V锥锥尾取压口所在的管道横截面。可以发现,无论在单相气体还是气液分层流条件下,锥尾取压口附近(r/R=0,0D截面)流速基本均为0,说明锥尾取压口附近的流动较为稳定,有利于低压测量;当来流为单相气体时(图9(a)),上游-1D处流动较为规则;从下游1D截面上的流速分布可知,从管道中心轴线r/R=0沿Y轴方向到r/R=1范围内,流速先减小后增大,这是由于该范围位于锥尾尾涡区域之内(图8),尾涡的影响使得流速分布发生变化。当来流为分层流时,位于尾涡区内的截面上也存在类似的速度分布(图9(b)~(d))。对于分层流,管道上下速度并不对称,上部速度大于下部速度,且表观液速越大,其不对称性越明显;速度分布亦与图8的尾涡分布特征相吻合。
在同一截面上,随着表观液速增大,沿Y轴方向的上部流速越来越大,而下部流速越来越小,如图10所示。由图7可知,流体流过V锥之后,压力恢复位置与尾涡的影响密切相关。当表观液速增大时,V锥差压也随之增大,同时下游恢复压力也越小,压力损失越大。对于分层流来流,下游压力恢复位置受表观液速影响较小(图11),这与尾涡对下游流动的影响规律相一致。
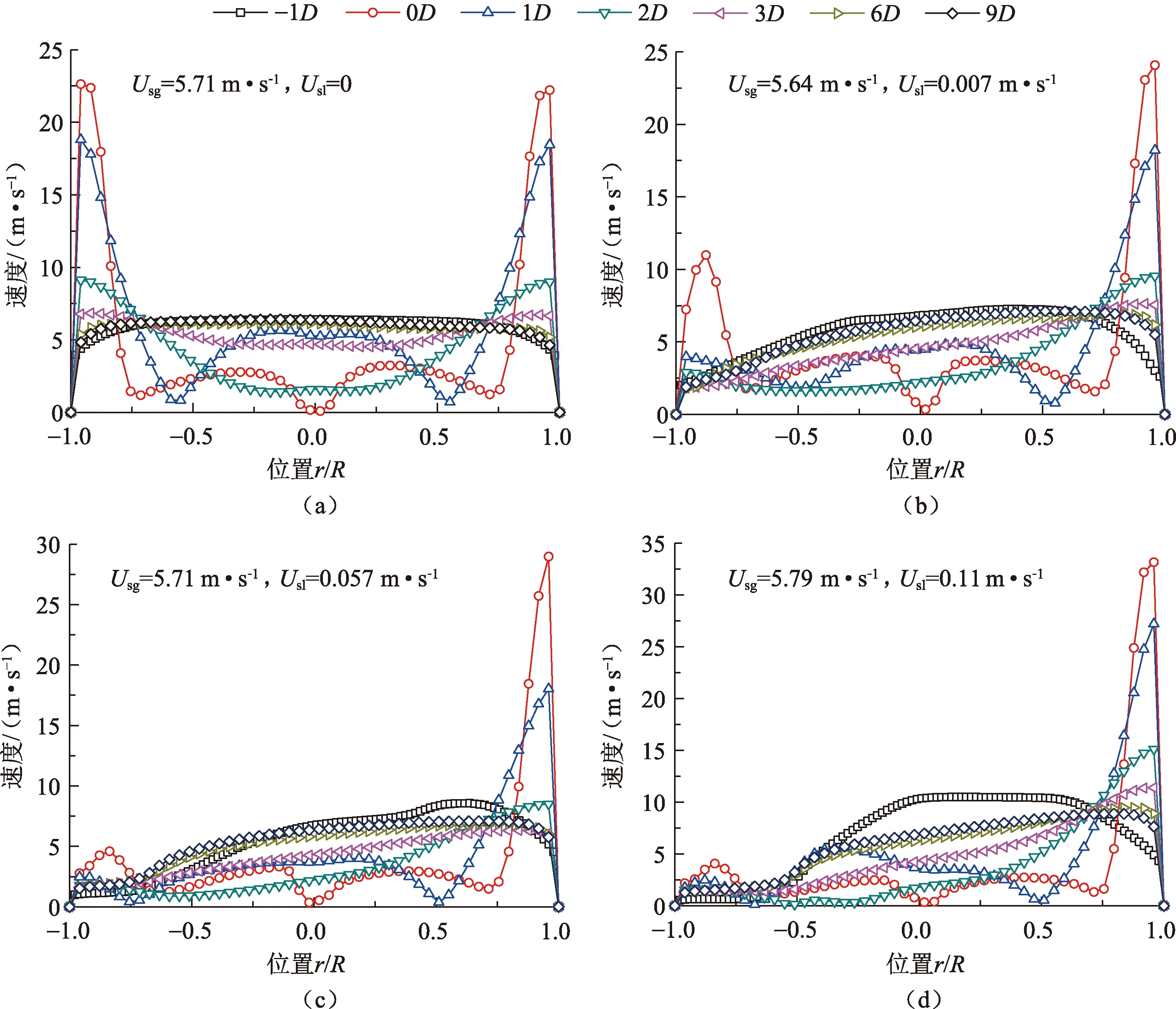
图9 不同横截面上沿Y轴方向的速度分布Fig.9 Velocity along Y axis direction under different cross sections
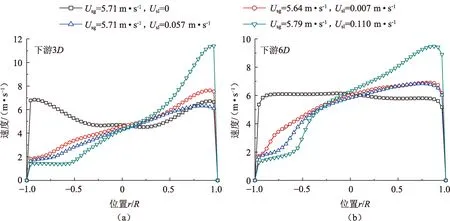
图10 V锥下游3D和6D截面上速度沿Y轴的分布随表观液速的变化Fig. 10 Velocity along Y axis direction with different superficial liquid velocity at 3D and 6D downstream V-cone
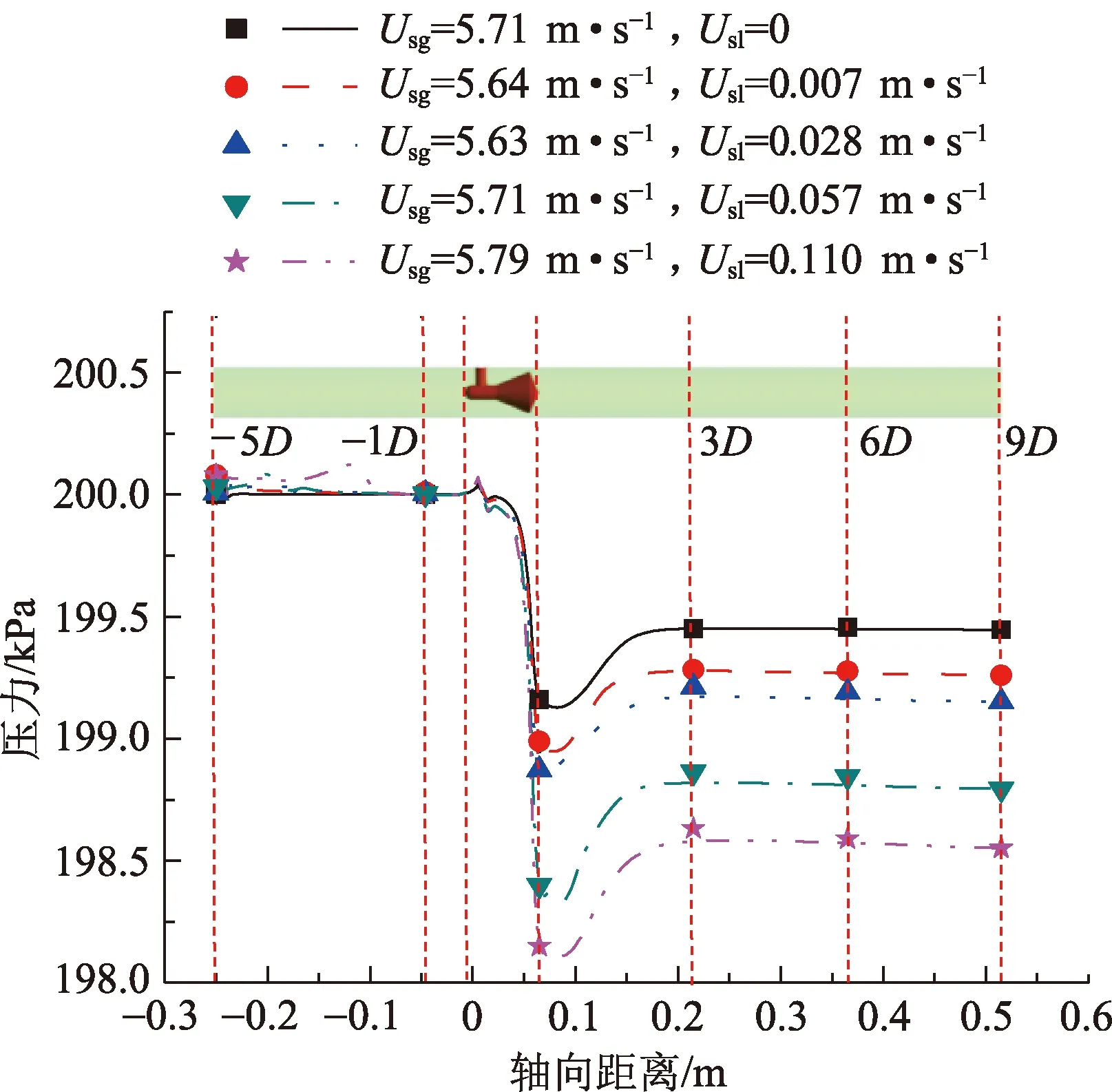
图11 不同表观液速下壁面静压力沿流动方向X的分布Fig.11 Wall static pressure along flow direction X under different superficial liquid velocity
2.2 气液相分布变化及其对测量影响
对V锥上游1D、V锥前端、锥尾取压口所在的管道截面及下游3D和6D处管道横截面上的液相分布进行分析。当来流为分层流时(图12(a)Usg=5.64 m·s-1,Usl=0.007 m·s-1;(b)Usg=5.63 m·s-1,Usl=0.028 m·s-1;(c)Usg=5.71 m·s-1,Usl=0.057 m·s-1;(d)Usg=5.79 m·s-1,Usl=0.11 m·s-1),气相中液相极少,流经V锥后,尾涡卷吸少量液体,同时在喉部高速射流作用下,管道下部液膜变薄,在V锥下游一定距离处才逐渐恢复;喉部射流的影响还导致液体发生飞溅,并有少量液体进入气相中。试验中还发现,气液两相流流经V锥,液膜在后锥体表面吸附,而在尾涡的影响下,液膜并没有完全覆盖后锥体表面,而是存在一个液膜边界,使得取压口附近基本没有液体分布(图13)。液相在V锥表面的这种分布是由“科恩达效应”(Coanda effect)引起的。尾部取压口附近基本没有液相分布,从而使得低压取压孔处于一个相对稳定的流动环境中,十分有利于气液两相差压测量。
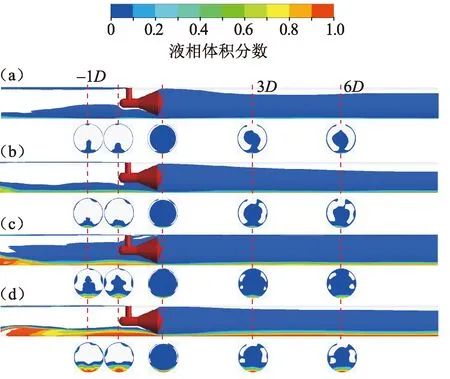
图12 液相体积含率分布Fig.12 Water volume fraction

图13 试验观察到的锥后液体分布Fig.13 Liquid distribution observed in experiment
3 结 论
(1)V锥锥尾下游形成大尺度的尾流漩涡。分层流来流条件下,由于液相主要分布在管道下部,因此下部流速较低,同时射流强度较弱,导致尾涡呈现上部大下部小的分布形态,表观液速越大,尾涡下游端点越向管道下部倾斜。气液两相流的平均密度与黏度均比单相气体中的高,以及V锥喉部环形射流撞击管壁产生的反弹液滴扩散现象,是导致V锥后尾涡特征发生变化的主要原因。
(2)V锥下游压力恢复长度和横截面上的速度分布与尾涡长度和形状变化密切相关。对于分层流,管道上下部速度并不对称,上部速度大于下部速度,其不对称性随表观液速增大而增加。
(3)锥尾取压口附近的流动较为稳定,且锥尾取压孔附近液相含量极低,使得低压取压环境较为稳定,进而有利于差压测量。
