基于局部等效方法的深水水下井口半解耦分析模型
2019-06-27畅元江姬景奇李家仪许亮斌盛磊祥
畅元江, 王 健, 姬景奇, 李家仪, 许亮斌, 盛磊祥, 乔 畅
(1.中国石油大学(华东)海洋油气装备与安全技术研究中心, 山东青岛 266580;2.中海油研究总院, 北京 100027)
深水水下井口在隔水管波致振动和涡激振动以及浮式钻井装置运动的激励下,其内部出现动态响应和循环交变应力,易发生疲劳损伤甚至失效。1982年,英国北海西舍得兰群岛附近海域,钻井隔水管涡激振动导致井口在服役仅29 d即发生疲劳失效[1],于是对深水水下井口进行准确的疲劳评估能够有效预防失效事件的发生,减小钻完井作业的风险。迫切需要研究并提出一种准确快速的水下井口动态响应精细分析方法和理论模型。目前,对于水下井口的研究主要集中在承载能力和稳定性、井口结构等内容[2-4],进行隔水管-井口系统疲劳分析时往往只是对水下井口进行简单建模[5-9]。Buchmiller等[10]指出高压井口疲劳失效是大量海洋钻采事故发生的原因,提出井口结构优化措施。Reinas等[11]针对北海某井口导管焊缝疲劳断裂进行研究,对比分析不同边界条件对水下井口疲劳分析的影响。Evans等[12]综合考虑土壤、海况等因素,采用Flexcom软件对水下井口进行波致疲劳损伤评估,提出提高水下井口疲劳寿命的对策。Holm等[13]对隔水管-井口整体分析模型进行改进,提高了水下井口疲劳损伤评估数值模拟方法的准确性。Sunday等[14]结合隔水管监测数据,考虑顶张力、泥浆密度等因素对水下井口初始评估模型进行校正。Hφrte等[15]分别采用Monte-Carlo、Form/Sorm等方法对水下井口系统进行结构可靠性分析。DNV与SHELL、WOODSIDE、TOTAL等公司合作,提出水下井口疲劳评估的推荐做法,该推荐做法对水下井口疲劳评估具有重要的指导意义[16]。这些关于水下井口疲劳评估中虽对水下井口的动态响应分析方法进行较多研究,但并未给出系统性的理论模型和计算方法与流程。笔者以水下井口为对象,考虑土壤、导管、高低压水下井口以及水下隔水管柱之间的相互作用,提出水下井口局部等效的方法和以此方法为基础的水下井口半解耦分析模型,形成深水水下井口局部等效的流程。
1 深水水下井口系统
典型的深水水下井口系统如图1所示。深水水下井口分为低压井口和高压井口,低压井口和导管往往采用喷射法下入地层中,成为建井的基础。浸泡结束,当导管和低压井口稳定之后,继续钻进井眼到设计深度,然后下入高压井口和表层套管并进行固井。回收固井管柱后,采用隔水管下入防喷器组(blowout preventers,简称BOPs),BOPs通过液压连接器与海底高压井口进行连接和锁紧,后续作业均需要在钻井隔水管内进行[17]。处于连接模式的深水浮式钻井平台-隔水管-水下井口-导管-土壤耦合模型如图2所示。
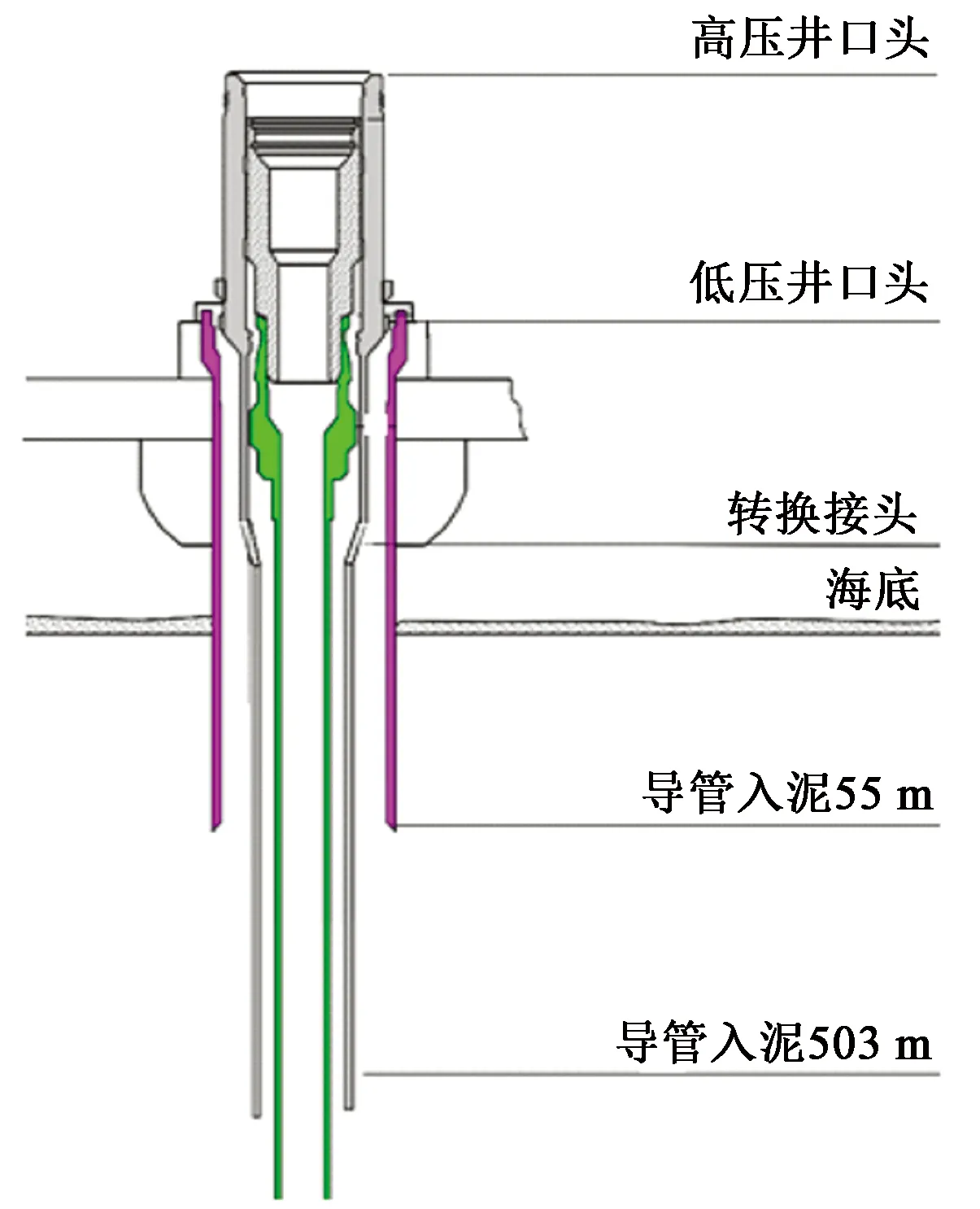
图1 典型水下井口系统结构Fig.1 Structure of typical subsea wellhead system
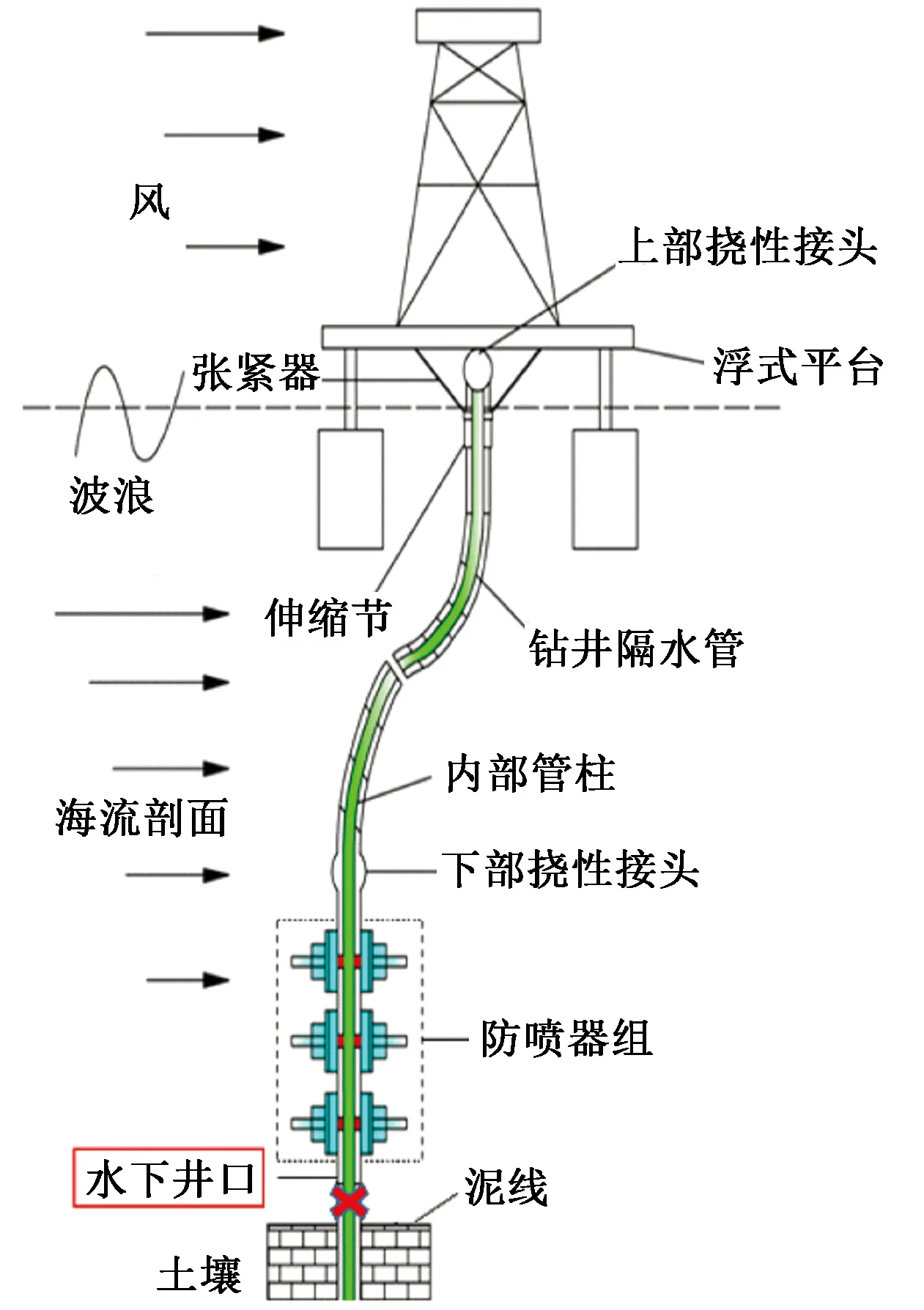
图2 浮式平台-隔水管-水下井口-导管-土壤耦合模型Fig.2 Coupled model of floating platform-drilling riser-subsea wellhead-conductor and soil
图2中,井口与导管要承受BOPs的重力、隔水管传递的横向力和弯矩[18]、土壤抗力以及高低压井口之间、水泥环与导管和表层套管之间、套管挂和高压井口之间的相互作用,从而导致水下井口的分析模型非常复杂。
传统的水下井口系统分析方法有两种,分别是耦合方法和解耦方法[19-20]。耦合方法模型中(图3),需要建立隔水管-井口-导管与土壤耦合的整体分析模型,模型的上部边界终止于上挠性接头与张紧器,浮式钻井装置运动作为强迫位移约束施加于上挠性接头和张紧器,下部边界终止于导管,导管下端采用固支约束。自伸缩节至导管的整个海洋钻井管柱系统采用管单元进行模拟;上、下挠性接头采用铰单元进行模拟,铰单元定义为连接、可转动类型,上部挠性接头的转动刚度一般设为0,而下部挠性接头的转动刚度随水深的增大而变大;张紧器作为等效垂直张力进行考虑。若采用解耦方法,则须将上述耦合模型在隔水管下部挠性接头处进行人为截断,建立两个子模型。第一个子模型包括平台边界-隔水管至下挠性接头,模型的底端采用固定端约束(图4(a))。第二个子模型包括下挠性接头至导管末端的部件,是一个可以考虑接触、交互等非线性作用的局部精细有限元模型(图4(b))。采用该方法时,先进行第一个子模型分析得到下挠性接头处的载荷边界条件,再将载荷边界条件施加到第二个模型进行分析以得到井口响应。
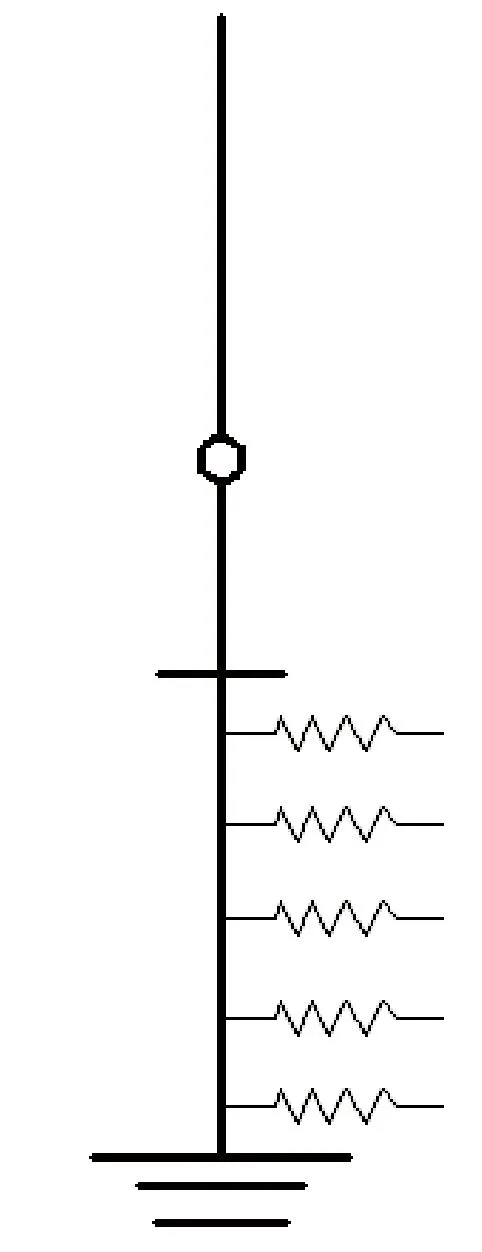
图3 水下井口的耦合模型Fig.3 Coupled model of subsea wellhead
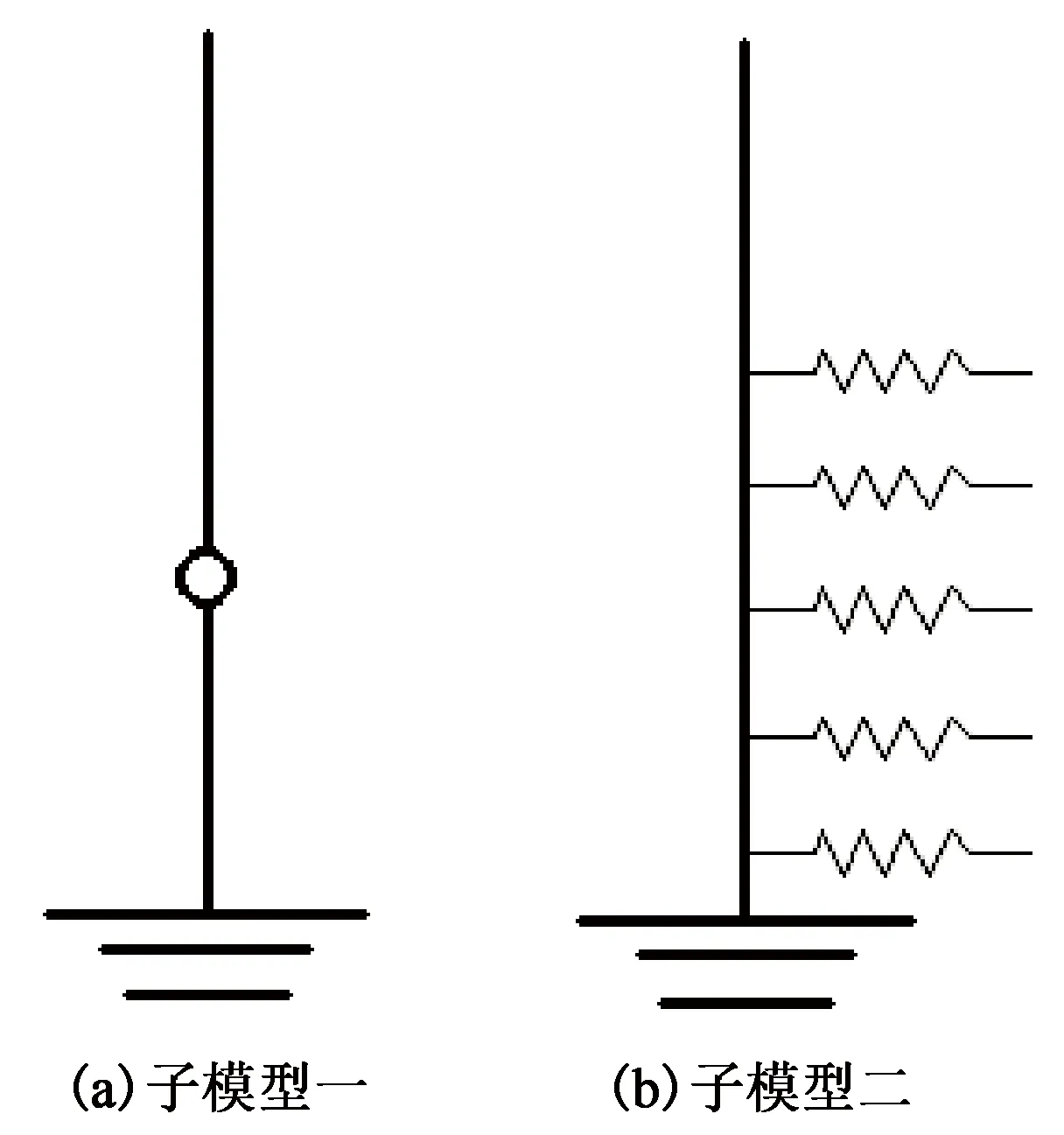
图4 水下井口的解耦模型Fig.4 Decoupled model of subsea wellhead
耦合方法须建立隔水管-井口-导管与土壤耦合系统的整体分析模型,由于为整体模型,有限元建模时水下井口各部件只能采用梁单元进行模拟,虽然管土之间可以采用较多的非线性弹簧进行模拟,但是无法考虑水下井口系统各个部件之间的非线性相互作用,故降低了水下井口分析的精度。而采用解耦方法时,由于第一个子模型的底部采用固定端约束,与考虑管土相互作用的耦合模型相比,提取的隔水管底部挠性接头转角处的载荷和位移响应均过大,在进行水下井口局部分析时将导致井口响应预测不准确。
2 水下井口等效模型理论基础
2.1 水下井口等效模型
集成耦合与解耦方法优点的水下井口力学分析的半解耦等效模型如图5所示。底部边界条件为铰支,底部铰支点为坐标原点,水平方向为x轴,沿着梁的方向为y轴。
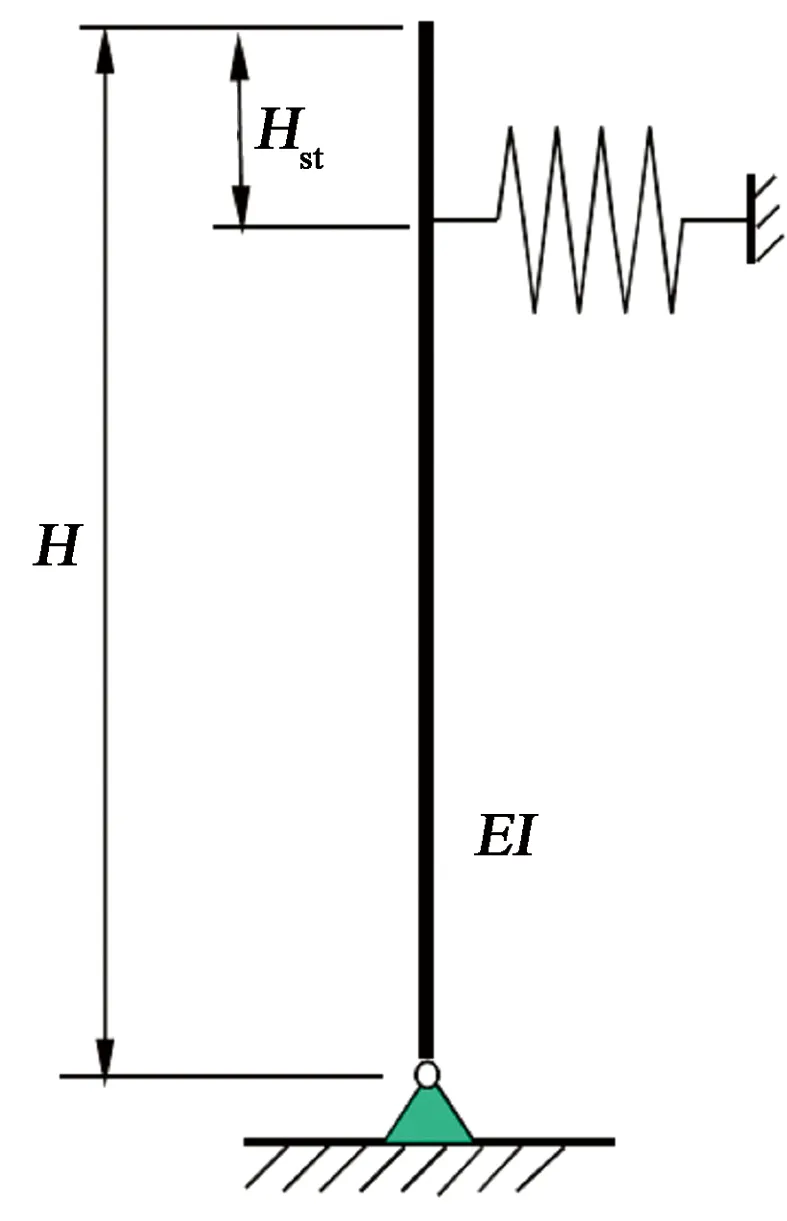
图5 水下井口系统等效模型Fig.5 Equivalent model of subsea wellhead system
整体分析过程中以梁和非线性弹簧的组合形式模拟水下井口系统,其中梁的底端约束为固支,该等效模型中梁截面为圆型,梁的顶端附近连接一非线性弹簧。等效模型中需要确定的参数为梁的高度H、梁的抗弯刚度、非线性弹簧的刚度K及弹簧距离梁顶部高度Hst。
等效后水下井口系统的变形过程可视为梁弯曲与梁转动的组合[21],如图6所示。
2.2 梁属性
实际作业过程中井口在基准面处(高压井口顶端)所受载荷为横向剪切力、弯矩和轴向力的组合。正常情况下井口系统变形远小于整体尺寸,根据力线平移定理,水下防喷器顶端所受横向剪切力可移至井口基准面处,只需附加一个力偶即可。
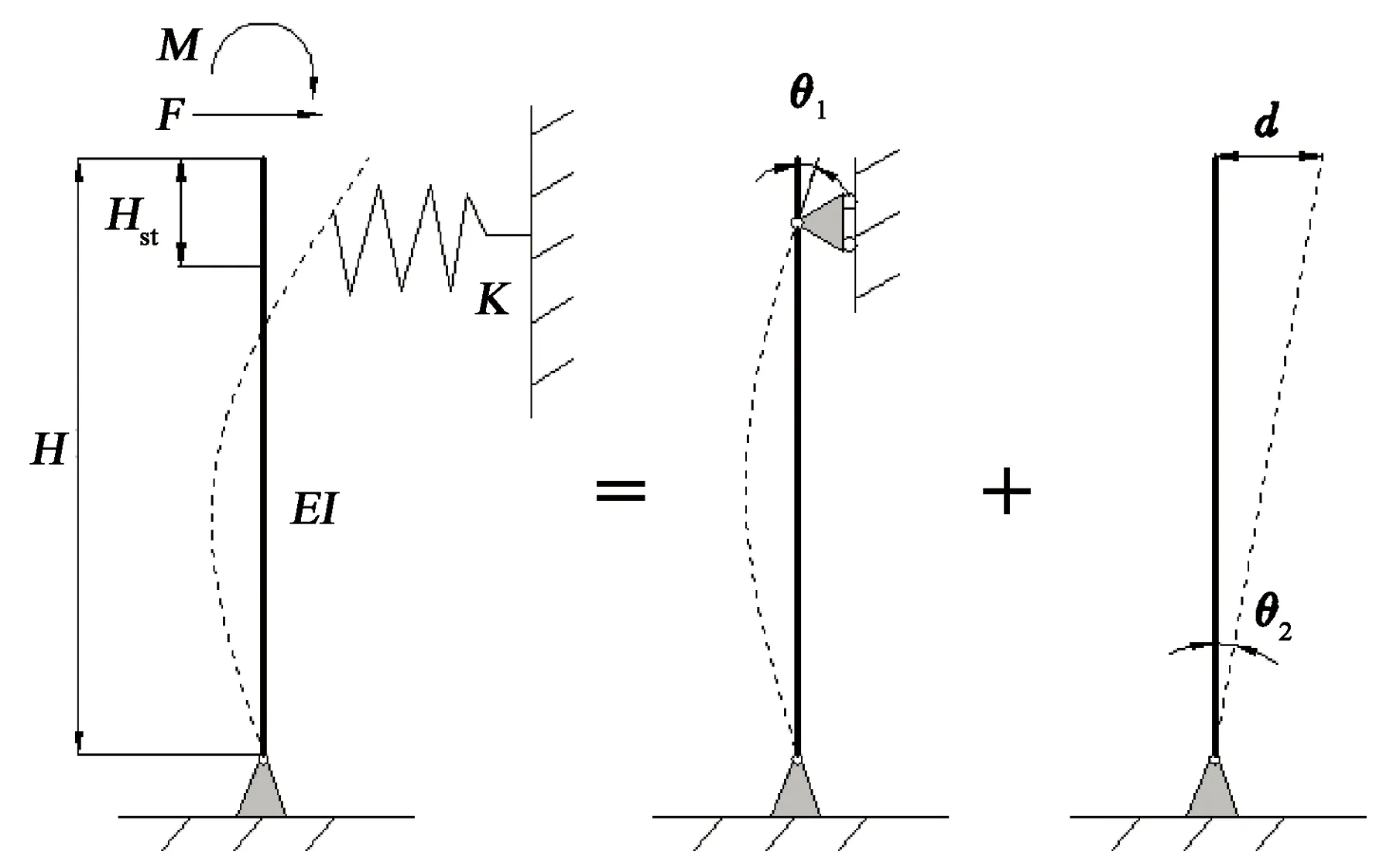
图6 梁弯曲与转动组合的水下井口变形示意图Fig.6 Diagram of subsea wellhead deflection by combination of beam bending and rotation
横向剪切力作用下两端铰支一端外伸梁的挠度和转角,弯矩作用下两端铰支梁的挠度和转角计算公式分别为
(1)
(2)
(3)
(4)
式中,yp为横向剪切力作用下梁末端挠度,m;P为横向剪切力,N;θp为横向剪切力作用下梁末端因变形产生的转角,rad;yM为弯矩作用下梁末端挠度,m;M为弯矩,N·m;θM为弯矩作用下梁末端因变形产生的转角,rad;L为两铰支的距离,m;a为梁外伸段的长度,m;E为弹性模量,MPa;I为梁的截面惯性矩,m4;x表示梁上某一点的位置,m。
平移至井口基准面后,横向剪切力作用下井口基准面挠度、转角,附加力偶作用下井口基准面处挠度、转角分别为
(5)
(6)
(7)
(8)
式中,y1为横向剪切力作用下井口基准面处挠度,m;θ1为横向剪切力作用下井口基准面处转角,rad;y2为附加弯矩作用下井口基准面处挠度,m;θ2为附加弯矩作用下井口基准面处转角,rad;F为横向剪切力,N;M为附加弯矩,N·m。
井口基准面因转动产生的挠度、转角为
y3=Hθ3.
(9)
式中,y3为井口基准面因转动产生的挠度,m;θ3为梁的转动角度,rad。
综合考虑横向剪切力、附加力偶作用以及转动,井口基准面的挠度、转角满足条件为
y1+y2+y3=y,
(10)
θ1+θ2+θ3=θ.
(11)
式中,y为井口基准面总挠度,m;θ为井口基准面总转角,rad。
由式(1)至式(11)可得
(12)
同理,弯矩作用下井口基准面挠度、转角分别为
(13)
(14)
井口基准面因转动产生的挠度、转角为
(15)
综合考虑弯矩作用和转动,井口基准面的挠度、转角满足条件为
(16)
(17)
由式(13)至式(17)可得
(18)
联立式(12)和式(18)可形成方程组,该方程组中,Hst一般取0.5 m[16],可方便求出剩余两个未知量梁的抗弯刚度和H。
2.3 弹簧属性
等效模型中梁的底端可自由转动,弹簧的刚度为非线性,可通过在局部模型井口基准面处施加横向剪切力求解,求解原理为胡克定律,具体求解过程为
(19)
ds=θ3(H-Hst),
(20)
(21)
K=R/ds.
(22)
式中,R为弹簧处的横向力,N;ds为弹簧处的位移,m;θ3为梁的转动角度,rad;θ为横向剪切力作用下梁的总转角,rad。
3 水下井口局部等效方法与流程
3.1 等效流程
建立水下井口局部有限元模型,以局部模型为基础,等效流程如下。
(1)以局部模型为研究对象,计算步骤:①在水下防喷器顶端仅施加横向剪切力;②在水下防喷器顶端仅施加弯矩。计算后提取两种载荷条件下井口基准面的挠度与转角,进而得到二者与横向剪切力、弯矩的关系;
(2)选取横向剪切力与弯矩作用下挠度与转角参数,计算梁的属性;
(3)以横向剪切力计算结果为基础,计算非线性弹簧属性;
(4)得到基于局部等效方法的深水水下井口半解耦分析模型。
对所得水下井口半解耦分析模型进行静力学和动力学分析,并将分析结果分别与精细有限元模型、解耦模型和耦合模型结果进行对比,验证所提出的水下井口半解耦分析模型的精度。
3.2 水下井口局部有限元模型
3.2.1 模型范围
建立水下井口局部有限元模型之前,需要确定局部模型的范围。为避免底部边界条件对水下井口应力产生影响,模型下边界应在泥线以下至少50 m,局部模型上边界取下挠性接头处[20]。
水下井口系统由外到内依次包括低压井口与导管、高压井口与表层套管、中间套管、油层套管等,连接状态下水下井口的载荷主要由高压井口与表层套管、低压井口与导管承受,其他部件不承受或承受很少载荷。因此,可以建立包含导管、表层套管和技术套管的水下井口局部有限元模型。
水下井口局部有限元模型较大,在保证精度的前提下为提高计算效率采取如下措施:水下井口系统有限元模型包含实体单元和梁单元,其中高压井口与低压井口结构复杂且包含接触关系,导管、套管上部含接头、焊缝等疲劳热点的部位采用实体单元建模,下部无疲劳热点区域采用梁单元建模。梁单元第一个节点与实体模型下端面耦合。
3.2.2 边界条件
土壤抗力对水下井口系统的应力分布起到重要作用。从有限元建模角度,目前有两种方法用于模拟土壤作用:①建立土壤实体模型;②以非线性弹簧模拟土壤抗力。以南海实际已钻井为例,当水深达到600 m,水下井口系统导管通常长达80 m,采用实体单元模拟土壤会导致模型过大,计算效率低下。以非线性弹簧模拟土壤抗力简便易行,准确度较高,能够极大地缩短计算时长。
水下井口模型为实体模型,无法直接建立非线性弹簧。建模过程中,先将导管的实体模型分割成多个长度相同的单元区域,在单元区域中心轴线位置建立参考点,并将参考点与单元区域的外表面耦合,耦合方式不引入附加刚度,土壤弹簧连接到参考点上,梁单元区域的土壤弹簧直接连接到节点上。由于所建水下井口模型为1/2对称模型,土壤对导管的抗力只须施加1/2。导管与土壤之间通过非线性弹簧耦合,其模型如图7所示。
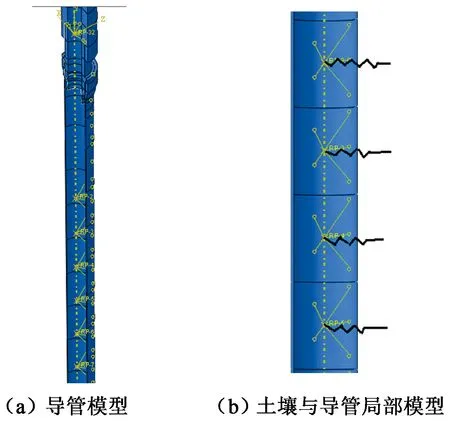
图7 导管与土壤耦合模型Fig.7 Coupled model of conductor and soil
根据钻井工艺流程,下入表层套管和高压井口后,在导管与表层套管环空中注入水泥,为准确模拟高低压井口间的受力,水泥环采用生死单元,在高压井口与表层套管重力施加后发挥作用。导管与水泥环底端采用固定边界条件,模型横截面建立对称约束。
3.2.3 载荷施加
水下井口系统静态轴向载荷包括套管重力、BOPs重力和过提力。其中套管重力随作业阶段的不同产生变化。高压井口与表层套管重力以集中力形式施加在表层套管底端,BOPs重力以集中力形式施加在其重心处,过提力作用于隔水管底部总称顶端,套管挂、技术套管以及其他内部套管重力施加在技术套管底端。水下井口系统的横向载荷包括横向剪切力和弯矩。横向剪切力和弯矩施加于BOPs顶端。考虑模型对称性,上述载荷只需施加其值的1/2即可。
水下井口系统精细有限元模型如图8所示。
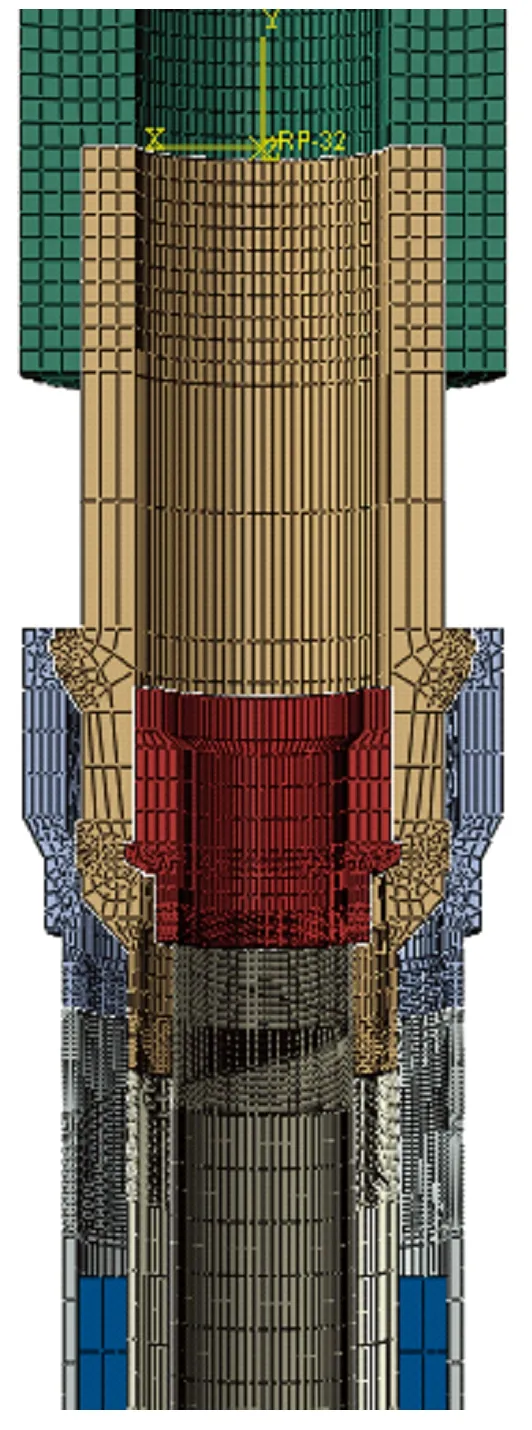
图8 水下井口系统精细有限元模型Fig.8 Fine finite element model of subsea wellhead system
4 算 例
4.1 基本参数
以南海某海域水下井口为例,水深为628 m,流剖面采用南海一年一遇流剖面[6],波浪基本参数见表1。此外,固井水泥环密度取1 560 kg/m3,弹性模量为18 GPa,泊松比为0.1。导管与表层套管参数见表2,土壤参数见表3。
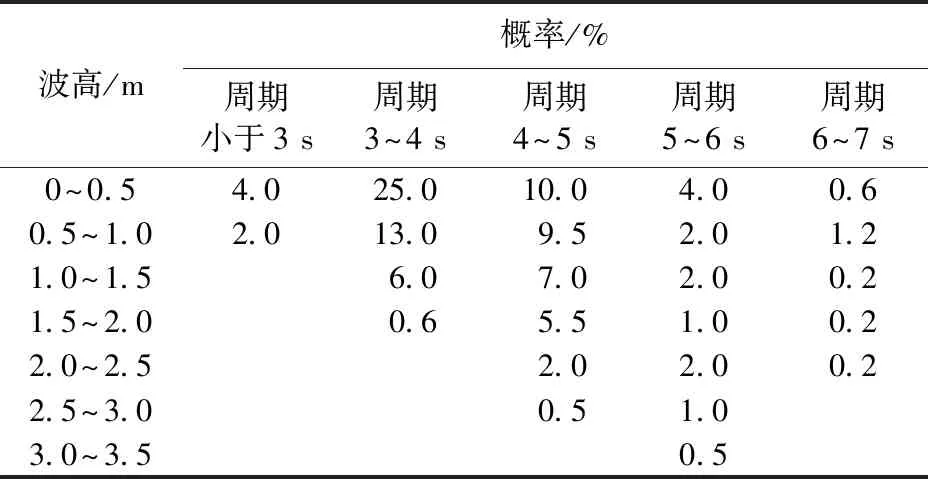
表1 南海某海域波高和周期联合分布

表2 导管/套管参数
注:导管总长度为68 m,外径为762 mm,其中上部导管长度约24.38 m,壁厚为38.1 mm,其余部分壁厚为25.4 mm;对于表层套管:上部长度为18.29 m,外径为508 mm,壁厚为15.875 mm,其他部分外径为339.7 mm,壁厚为10.9 mm,采用变径接头进行过渡。
4.2 等效参数计算
以本文所提出的等效模型理论为基础,采用水下井口系统局部有限元模型,在BOPs顶部分别施加横向力与弯矩,提取高压井口顶部位移、转角。部分井口基准面位移、转角与横向力关系见表4,部分井口基准面位移转角与弯矩关系见表5,等效梁的属性计算结果:Hst、H分别为0.5和9.650 6 m,抗弯刚度为797.02 MN·m2。
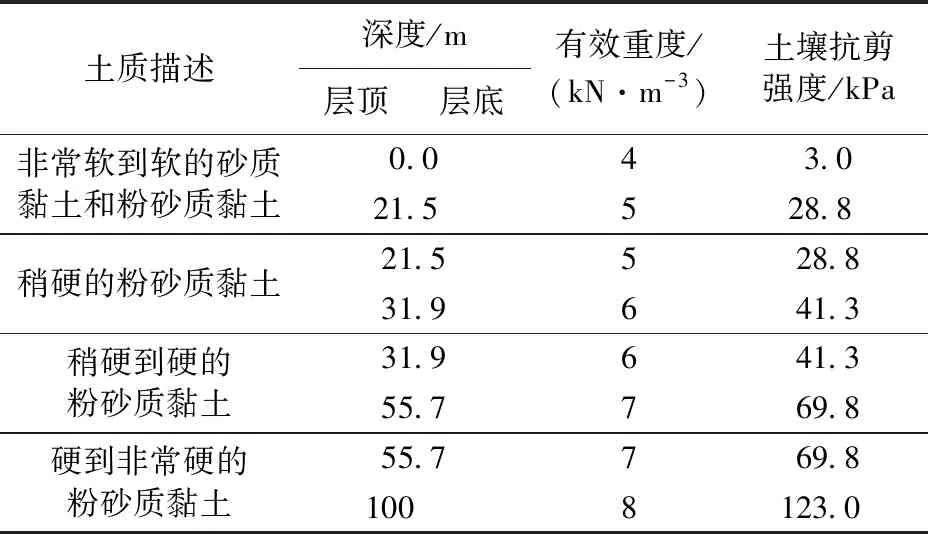
表3 土壤参数
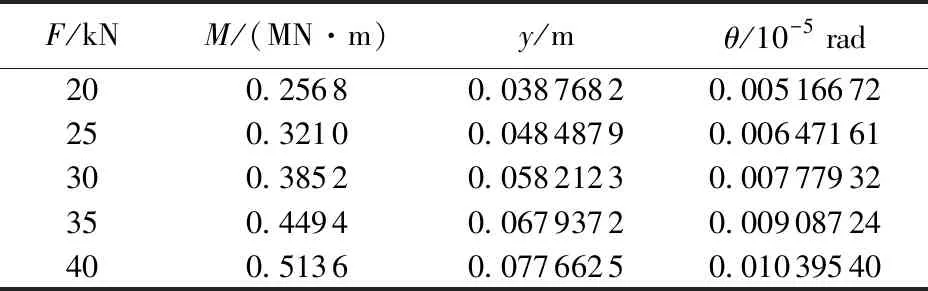
表4 横向力作用下井口基准面位移、转角

表5 弯矩作用下井口基准面位移、转角
计算得到的等效模型中弹簧非线性刚度曲线如图9所示。
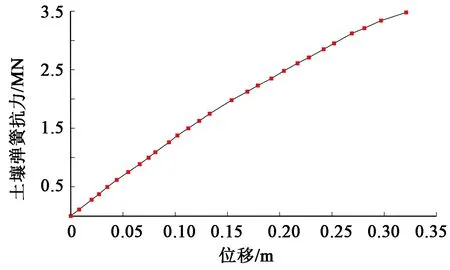
图9 等效非线性弹簧刚度曲线Fig.9 Stiffness curve of equivalent nonlinear spring
4.3 结果验证
从静力和动力两个层面对等效模型进行精度验证。从静力特性的角度来说,分别建立水下井口系统精细有限元模型(图8)和包含梁与弹簧组合的等效模型(半解耦模型),然后分别施加弯矩和横向剪力,再分别提取两种载荷条件下井口基准面转角与位移进行对比,对比结果如图10、11所示。由图10、11可知,在横向剪切力和弯矩作用下,采用等效模型的井口基准面位移及转角与采用精细模型的计算结果吻合良好,这表明进行水下井口系统静力学特性分析时可以用等效模型代替精细模型,计算和建模可得到相当大的简化,且具有同样的计算精度。
在同样的载荷工况下,分别采用解耦、耦合与半解耦方法对水下井口进行动力学分析,计算时长取值大于105s。分别提取3种方法的井口基准面处单元的弯矩时间历程,并对其进行雨流计数,得到循环弯矩幅值和对应的循环次数,结果如图12所示。
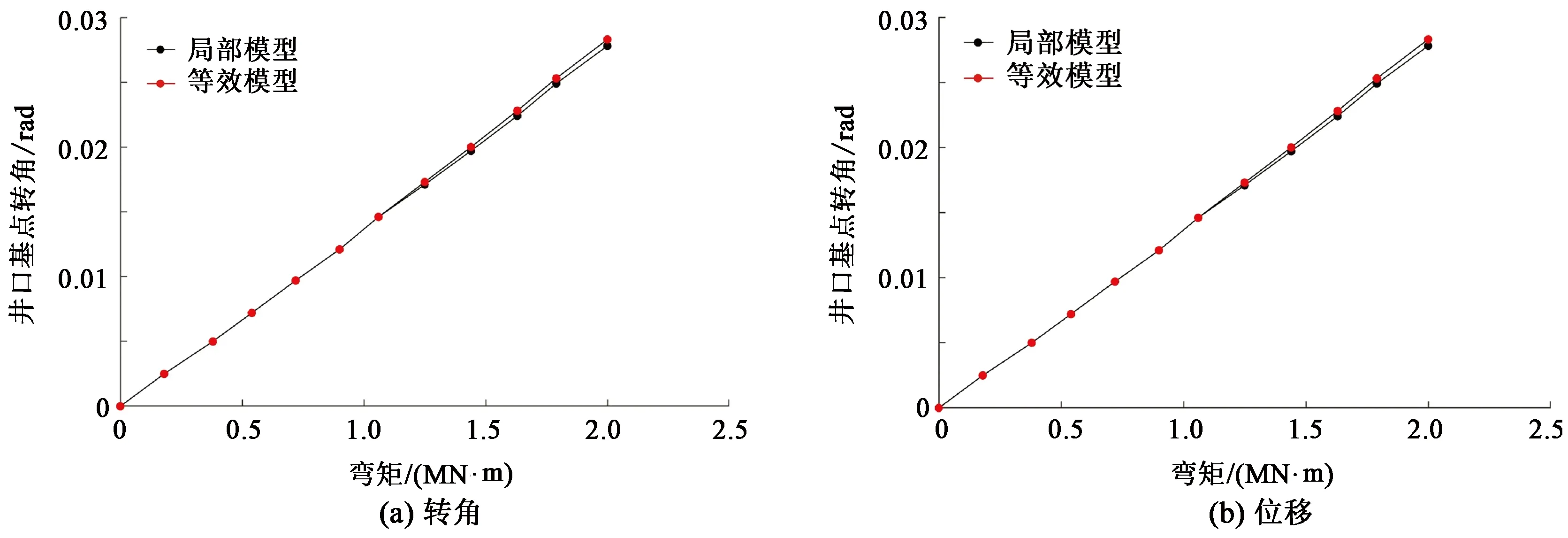
图10 弯矩作用下半解耦模型与精细模型计算结果对比Fig.10 Calculated results comparison of semi-decoupled and fine model under bending moment
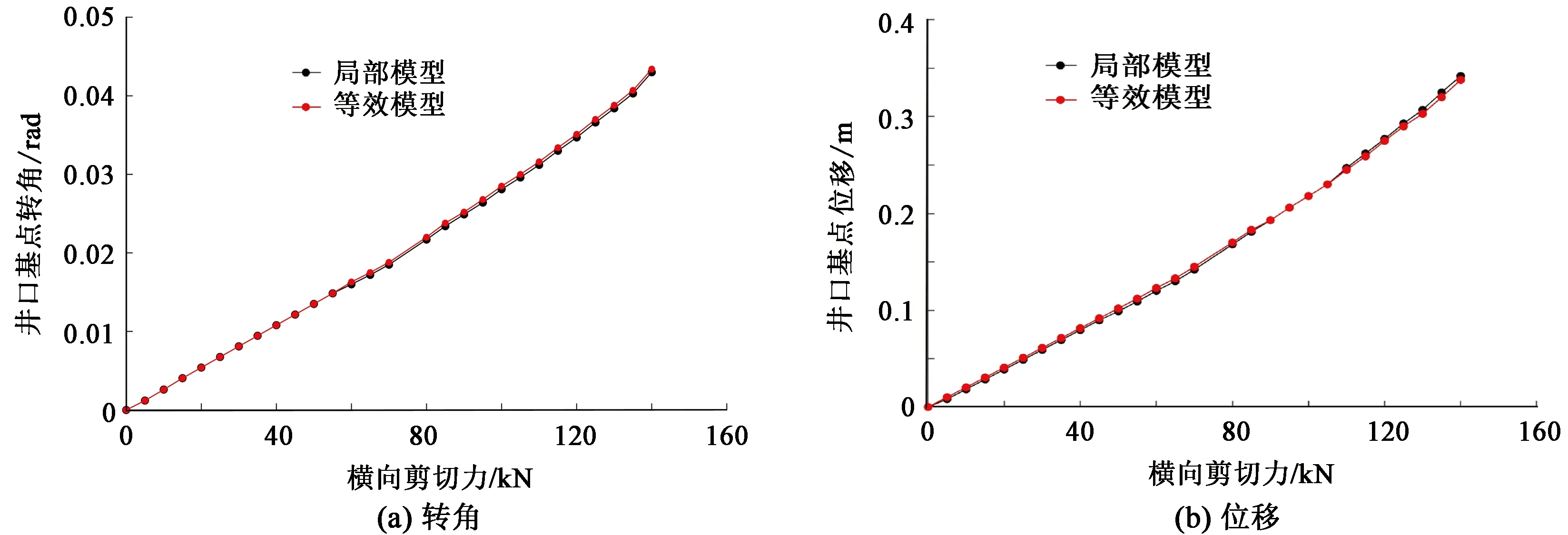
图11 横向剪切力作用下半解耦与局部模型计算结果对比Fig.11 Calculated results comparison of semi-decoupled and fine model under horizontal force
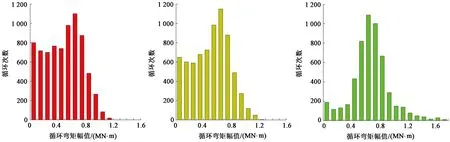
图12 半解耦、耦合和解耦模型井口弯矩Fig.12 Statistic bending moment of semi-decoupled、coupled and decoupled models
由图12可知,采用半解耦方法和耦合方法所得井口基准面循环弯矩分布较一致,两种方法所得弯矩循环次数在高幅值区域基本相等;在低幅值区域,采用半解耦方法得到的弯矩循环次数相对较高,表明半解耦方法捕捉的动态响应应力幅值范围更广。而采用解耦方法得到的结果与上述两者差别较大,解耦方法得到的高幅值弯矩循环次数增多,低幅值弯矩循环次数减少,其原因在于解耦方法的整体模型所取的边界条件为底部固定端约束,造成刚度较大导致计算精度较差。
在总的计算时长内,不同弯矩幅值条件下累积循环次数计数结果对比如图13所示。由图13可知,在整个计算分析的循环弯矩幅值范围内,采用耦合方法、半解耦方法和解耦方法所得井口基准面弯矩总循环次数(N)分别为7 191、7 502和5 450。耦合方法中无法考虑水下井口系统各部件之间的细节关系,计算精度较高。解耦方法由于自身模型缺陷的原因,计算精度较低,对水下井口的计算过于保守。而半解耦方法采用等效模型,在建立隔水管-水下井口-导管-土壤整体模型的同时,还可以考虑水下井口系统各个部件之间的细节关系,精度和计算效率相对最高,比较方便在工程中推广使用,可为开展井口疲劳评估提供一种可靠的计算方法。
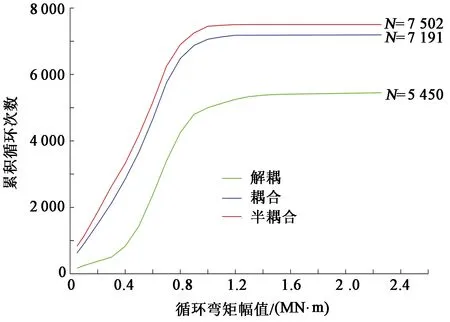
图13 三种模型井口弯矩累积循环次数比较Fig.13 Comparison of accumulated cycle number of bending moment for three models
5 结 论
(1) 提出深水水下井口半解耦分析模型的建模方法将水下井口系统等效为非线性弹簧和等效梁的组合模型,实现了水下井口系统的局部等效。
(2) 在横向剪力和弯矩作用下,局部模型和等效模型的井口基准面位移及转角非常吻合,水下井口静力学分析时等效模型可替代局部精细模型。
(3) 耦合方法精度较高但无法捕捉到井口的局部响应,解耦方法虽建模简单但计算精度较低且结果过于保守,而半解耦分析方法既可以捕捉到井口局部响应,精度和计算效率也相对最高。
