基于线性滑动模型的裂缝性地层声波测井响应数值模拟

欧伟明, 王祝文, 宁琴琴, 徐方慧, 于 洋

(吉林大学地球探测科学与技术学院,吉林长春 130026)

一般裂缝性储集层具有相当高的渗透率,裂缝对油气藏的开采非常重要[1-3]。裂缝的存在会使声波测井的波形发生很大的变化,因此掌握裂缝对井中声波传播的影响规律,将对裂缝的检测和评价起到重要作用。国内外关于裂缝对井中声波传播影响方面已经做了大量的研究,一方面根据实际声波测井和相关物理实验的数据进行分析;另一方面把裂缝当作一个流体薄层,采用有限差分和有限元方法数值模拟。Morris等[4]利用声波测井资料中纵、横波幅度检测裂缝的位置。Paillet[5]根据声波测井资料中斯通利波和横波幅度的变化研究在裂缝附近的声波传播。Zlatev等[6]采用物理实验模拟全波列声波在含有裂缝的井中传播,研究裂缝宽度和倾角对波形的影响。采用数值模拟的方法能避免人为误差、节约实验成本。魏周拓等[7]对井旁不同角度和不同位置裂缝的全波波列进行了数值模拟。龚丹和章成广[8]应用三维应力-速度有限差分方法模拟含有倾斜裂缝地层中的井孔声场。Matuszyk等[9]采用频率域有限元法模拟在裂缝性地层中井中声波的波形。阎守国等[10]运用变网格有限差分法模拟井中声波在含有倾斜薄裂缝的孔隙地层中的传播。闫怡飞等[11]采用有限元方法模拟存在井旁裂缝情况下的反射波波形特征。由于裂缝的宽度一般小于1 mm,这些流体薄层模型需要用非常小的网格来描述裂缝宽度,这会增加大量的计算时间。在地震波传播方面,裂缝经常被看作是一个位移不连续的线性滑动界面[12-13]。在线性滑动模型(LSM)中,假定裂缝可以用一个界面来表示,穿过这个界面,由地震波引起的位移是不连续的,而应力保持连续。位移矢量的跳跃与应力矢量之间的线性关系由断裂柔度张量决定。Coates和Schoenberg[14]在线性滑动模型基础上引入一种等效介质理论来模拟与裂缝相交的有限差分网格的性能。Wu等[15]采用有限差分法模拟一个开放的充满流体裂缝的地震响应,对比了线性滑动模型和流体薄层模型,并发现这两种模型具有很好的一致性,但计算前者所需要的时间非常少。吴国忱和秦海旭[16]采用线性滑动模型模拟裂缝性介质的响应。目前还没有线性滑动理论在声波测井响应模拟方面的研究。鉴于采用线性滑动模型模拟计算的高效性,笔者基于线性滑动模型,采用有限差分法来模拟不同裂缝宽度和不同裂缝条数情况下的全波列声波测井响应,研究水平的线性滑动裂缝对声波波形的影响规律。

1 线性滑动模型

为了把线性滑动模型的裂缝合并到有限差分网格中,Coates和Schoenberg[14]提出等效介质理论。该理论中,所有含有裂缝的有限差分网格单元被模拟裂缝的等效各向异性网格代替,如图1所示。等效介质理论被用于计算有裂缝穿过的有限差分网格的弹性参数。等效介质理论计算需要每个差分网格的参数,包括基岩的拉梅常数λ和μ、裂缝宽度h、每个网格包含的裂缝长度L以及法向和切向的裂缝柔度ZN和ZT。

τij=cijklekl.

(1)

式中,τij为应力;cijkl为弹性张量;ekl为应变。在等效介质理论中,公式(1)中的弹性张量定义为

(2)

图1 在有限差分模型中代替一条水平裂缝的各向异性的网格Fig.1 Anisotropic grids instead of a horizontal fracture in finite-difference model

对于二维模型,r=λ/(λ+2μ),δN=ZN(λ+2μ)/[L+ZN(λ+2μ)],δT=ZTμ/(L+ZTμ)。当δN和δT的值为0时,表示有限差分网格中没有裂缝。对于开口的、充满流体的裂缝,ZN=h/Kf,ZT=∞(Kf为流体体积模量)。公式(2)描述的等效弹性介质是横向各向同性的。如果裂缝的倾角和网格之间存在角度,需要对方程进行旋转变换,得到每个网格的等效介质参数后,可以采用交错网格有限差分法来模拟各向异性介质。

2 模型和有限差分实现

2.1 计算模型

地层中一些裂缝是单独存在的,影响声波的传播;还有一些多条裂缝相距较近,它们组成裂缝带,共同作用于声波的传播。本文中要模拟的模型包括单条裂缝模型和多裂缝模型。如图2所示,夹在两个相同的弹性地层中的水平裂缝穿过充满流体的井孔,裂缝的宽度为h,裂缝带的宽度为H,井孔半径为a,a=10 cm。声源位于井轴上,裂缝或裂缝带的下表面到声源的距离d=2 m。在裂缝带中,裂缝的间距为5 cm。

图2 被无限长水平裂缝穿过的井孔模型Fig.2 Borehole model inserted by infinite horizontal fractures

2.2 有限差分方法

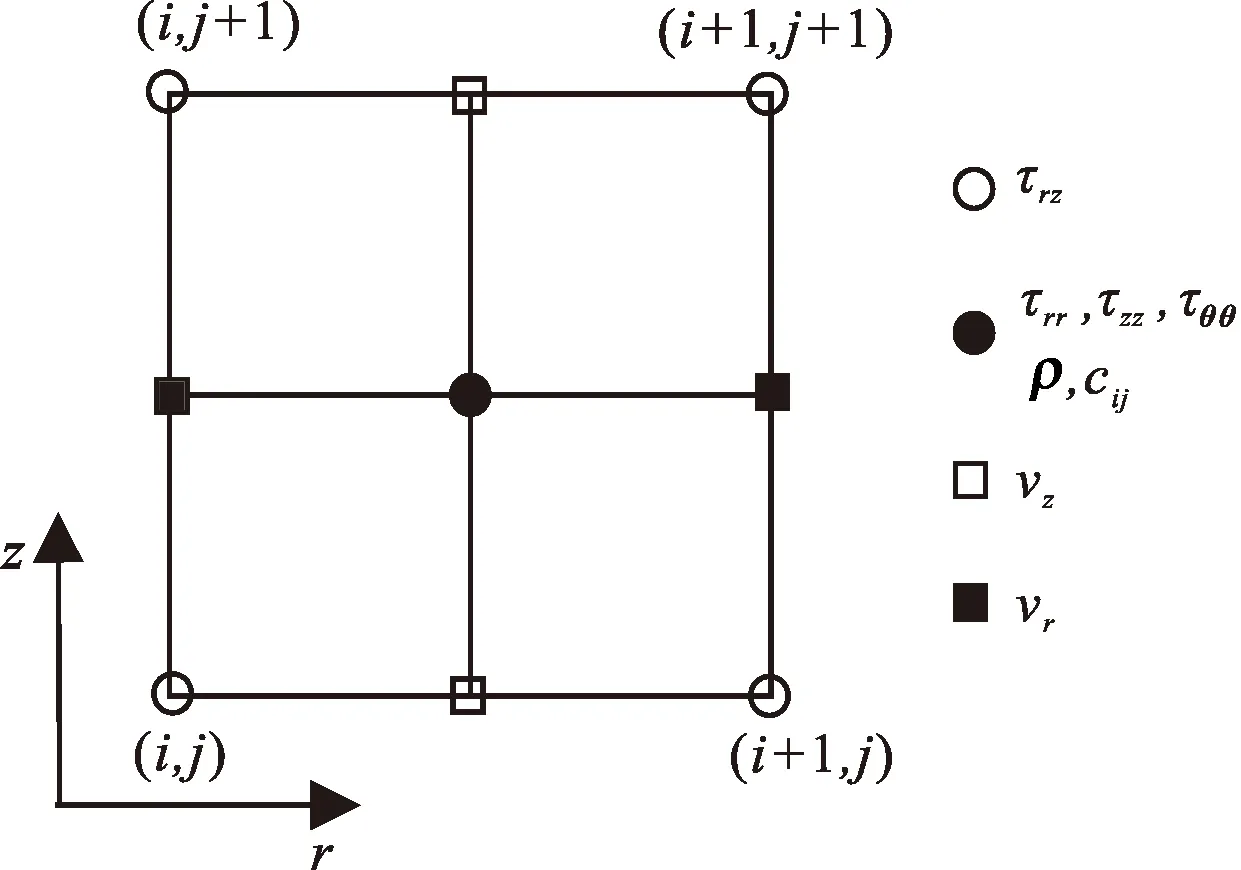
图3 介质参数和应力、速度分量在交错网格中的位置Fig.3 Position of medium parameters and stress and velocity components in staggered grids

由于井是圆柱形,使用柱坐标系来描述需要模拟的模型。因为模型具有对称性,可以将模型简化为在r-z平面上的二维模型。采用交错网格有限差分法[17-20]模拟弹性波在本文模型中的传播。介质的物性参数和应力、速度分量在交错网格中的位置,如图3所示。空心圆表示剪切应力,实心圆表示正应力,空心方形表示z方向上的速度分量vz,实心方形表示r方向上的速度分量vr。括号中的参数i和j分别表示r、z方向上的网格点数。在r、z方向上网格步长分别为Δr和Δz,Δr=Δz。二维柱坐标系下,时间上二阶、空间上二阶、声波在模型中传播的速度-应力方程为

(3)

式中,τrr、τθθ和τzz分别为r、θ和z方向上的正应力;τrz为剪切应力;上标n为时间层数;Δt为时间步长;Lr和Lz分别为r、z方向上的有限差分算子;σi为正向的算术平均算子,定义为σifi=(fi+fi-1)/2;参数ρ和μ分别为介质的密度和剪切模量。在介质的分界面上,分别对ρ和μ取算术平均值和调和平均值;在固-液分界面上,μ的值为0。

为了减小在计算期间的数值频散,空间网格的步长需要满足不等式:

Δr≤vmin/10fmax.

4.有利于党形成良好政治生态。党内政治生活与政治生态二者相互作用，密不可分。政治生活造就政治生态，政治生活是政治生态形成的基础；政治生态影响政治生活，政治生态是政治生活的集中反映。一段时间以来，由于党内政治生活存在宽松软的问题，一些地方和部门的政治生活出现庸俗化、随意化、平淡化的现象，给党内政治生态带来极大的负面影响。因此，良好的党内政治生态要从严肃党内政治生活中来。正如习近平同志所说：“党内政治生活、政治生态、政治文化是相辅相成的。”[4]

式中,vmin为模型中最小的纵波速度;fmax为声源的最高频率。对于二维的二阶交错网格有限差分法需要满足如下稳定性条件:

(4)

式中,vmax为模型中最大的纵波速度。本文中选取中心频率为10 kHz的声源,声源函数s(t)的表达式为

(5)

式中,f0为声源的中心频率;Tc为声源脉冲宽度,本文中Tc=2/f0。

3 数值模拟结果

3.1 单条无限长裂缝

根据公式的有限差分方程编写程序,模拟声波在被单条水平裂缝穿过的井中传播。模型的尺寸为6.4 m×2.56 m;根据有限差分的稳定性条件,选取差分网格的步长Δr为1 cm,时间步长Δt为1 μm。弹性地层的纵波速度和横波速度分别为3 570 m/s和2 170 m/s,地层密度ρ为2 350 kg/m3。井中流体的密度和纵波速度分别为1 000 kg/m3和1 500 m/s。在模型中加入非分裂完全匹配层吸收边界[21],消除模型边界产生的虚假反射波。

图4展示了在不同时刻t井中声波在含有水平裂缝的地层中传播的波场快照。虚线代表着井壁,声源位于z=500 cm和r=0 cm处,宽度为2 mm的水平裂缝位于z=300 cm处。声波沿着地层传播到模型边界后,声波被充分吸收了,地层中没有产生反射波,说明程序中加入的吸收边界是有效的。在1 ms时刻,井中纵波传播的距离最远,但它的能量非常小;之后是横波首波,它的能量比纵波大一些;传播距离最近的是斯通利波,它的能量最高。在1.5 ms时刻,井中横波首波和一部分斯通利波穿过裂缝,波的能量明显减小了很多。在2 ms时刻,井中可以看见明显的反射斯通利波和反射横波首波。

图5为模拟井中声波在单条水平裂缝模型中传播得到的波形。接收器的最小源距为1 m,接收器的间隔为0.2 m,水平裂缝位于源距上方2 m处。在裂缝上方的接收器记录的波列中,横波和斯通利波的幅度明显减小了。穿过裂缝后,横波幅度的骤降,说明了线性滑动裂缝对横波具有很强的衰减作用。由于裂缝引起波的强反射,在裂缝下面的波列中出现了反射横波首波和反射斯通利波。

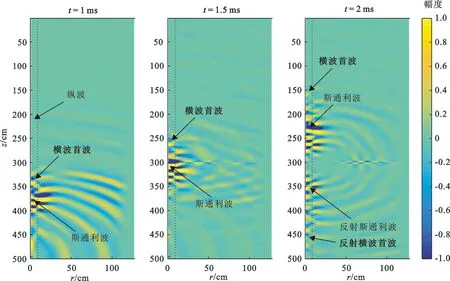
图4 在1、1.5和2 ms时刻的波场快照Fig.4 Acoustic wave field snapshots at 1, 1.5 and 2 ms respectively

图5 井中声波在单条水平裂缝模型中传播的波形Fig.5 Waveforms of borehole acoustic waves propagating in a single horizontal fracture model

图6展示了在裂缝上面不同源距的接收器所记录的透射波波形。在有裂缝和无裂缝情况下,纵波的波形几乎没有发生变化,可见裂缝对纵波的影响很小。即使宽度很小的裂缝,也使横波的幅度衰减了很多,这说明裂缝对横波的衰减作用很强。对于流体薄层模型,物理实验和基于有限元法的数值模拟也展现了裂缝会明显降低横波的幅度[6,9]。裂缝的存在使斯通利波的幅度也发生了明显的衰减,随着裂缝宽度的增加在同一源距斯通利波幅度的衰减程度增大。不同宽度裂缝对应的透射斯通利波的幅度非常接近,该现象说明在线性滑动模型中斯通利波幅度对裂缝宽度的变化不是很敏感。基于流体薄层模型的数值模拟表明随着裂缝宽度的改变,透射斯通利波的幅度发生了明显变化[8-9]。对于流体薄层模型,因为井中流体流入裂缝和裂缝散射,斯通利波发生衰减[22]。线性滑动模型忽略了流体流入裂缝的影响,因此它不能反映裂缝宽度与斯通利波衰减之间的关系。

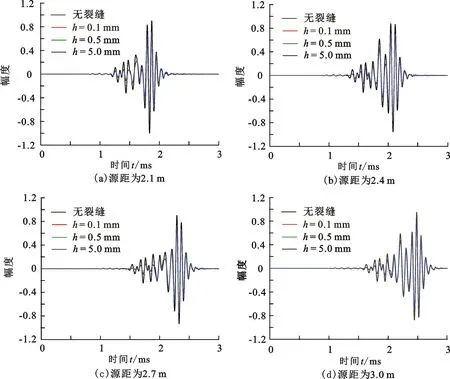
图6 不同源距的透射波波形Fig.6 Transmitted waveforms with different source distances

为了更清晰展示在不同宽度裂缝情况下,透射纵波和透射横波幅度的变化,用时间窗截取图6中的纵波首波和横波首波。图7和图8分别为不同源距的透射纵波和透射横波首波波形。在同一接收器下,将有裂缝与没有裂缝情况下纵波首波幅度作对比:图7(a)中前者稍微小一些;图7(b)中前者稍微大一些;而图7(c)和(d)中两者几乎一致。从这些现象可以看出:当接收器距离裂缝很近时,接收器记录的波列除了滑行波以外,还有由狭窄的裂缝口引起的散射波;由于这两种波重叠在一起,并且由于不同源距它们相位的差异不同,记录到纵波首波的幅度可能会增加也可能会减小。图7(a)中随着增加模型的裂缝宽度,纵波首波的幅度衰减程度增加,说明了宽度较大的裂缝产生的散射波对透射纵波幅度的影响也更大。由图8可以看出:随着源距的增加,即随着接收器到裂缝的距离增加,横波首波幅度的衰减程度增大;同一源距不同宽度裂缝对应的横波幅度变化很小;裂缝的存在使横波的相位发生了变化。

图7 不同源距的透射纵波首波波形Fig.7 Waveforms of transmitted compressional head wave with different source distances

图8 不同源距的透射横波首波波形Fig.8 Waveforms of transmitted shear head waves with different source distances

图9为源距为1 m的接收器记录的不同宽度裂缝情况下的反射波形。裂缝的宽度分别为0.1、0.5和5 mm。如图9所示,这3种不同宽度的裂缝对应的反射波曲线几乎重叠在一起,可见反射波的幅度对线性滑动模型的裂缝宽度的变化不敏感。

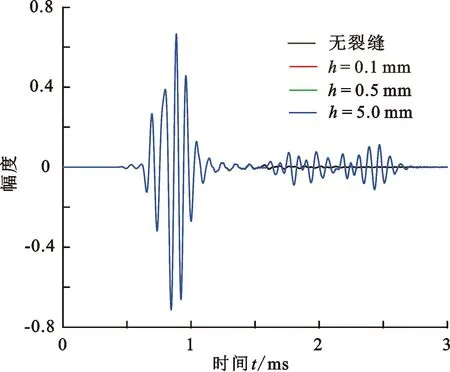
图9 不同宽度裂缝的反射波形Fig.9 Reflected waveforms of fractures with different widths

3.2 有限延伸距离的裂缝

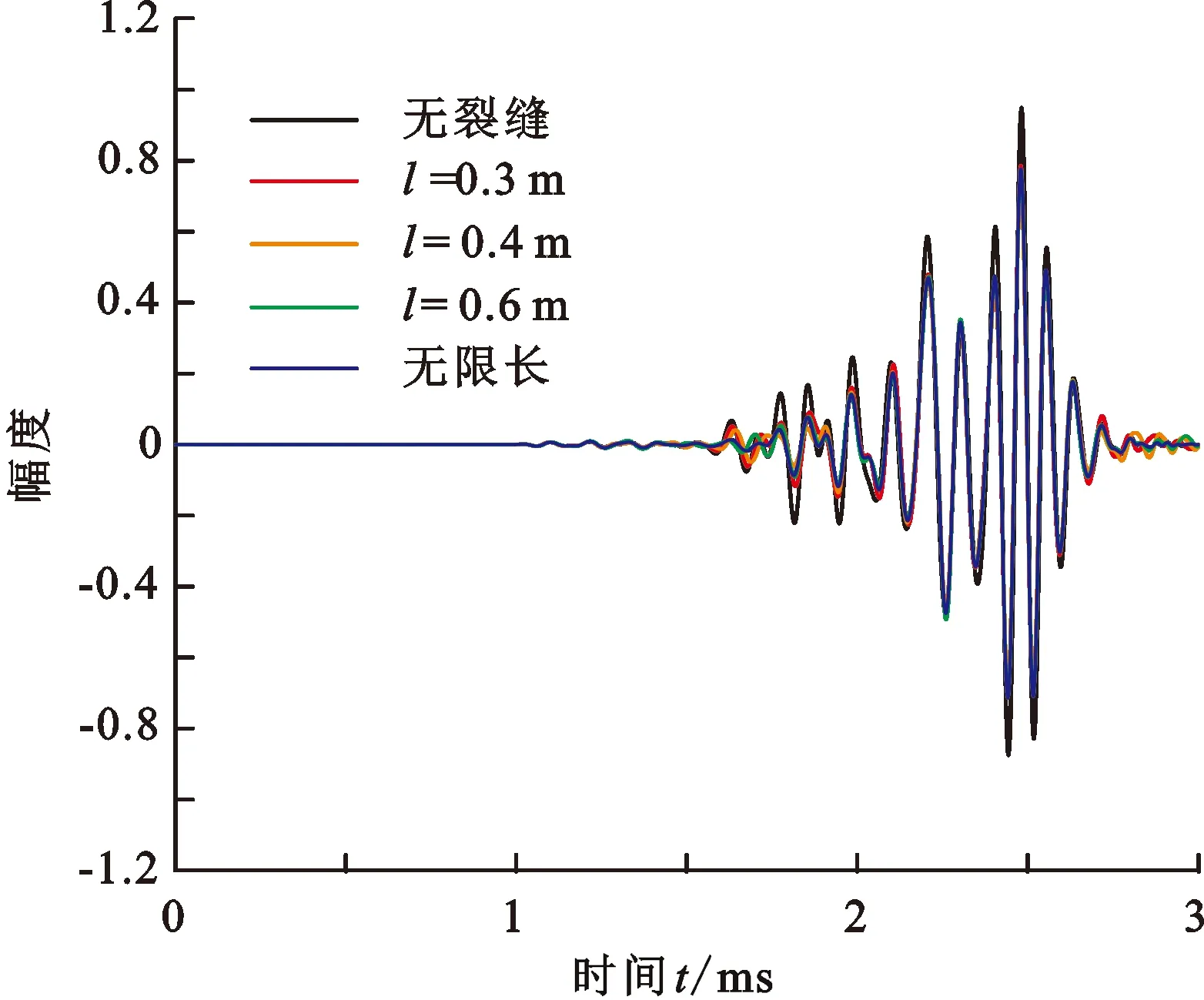
图10 不同裂缝延伸距离情况下的透射波波形Fig.10 Waveforms of transmitted waves with different extended distances of fractures

地层中的自然裂缝从井眼轴向径向延伸了有限距离,一些水压力缝的延伸距离很短[23]。假设水平裂缝从井轴向径向方向延伸有限的距离l,模拟井中声波在有限长裂缝模型中传播,研究裂缝长度对声波波形的影响。图10和图11分别展示了不同裂缝延伸距离情况下的透射全波、透射横波首波波形,接收器的源距为3 m。模型中裂缝的宽度均为1 mm,弹性地层的参数和图6中的相同。在图10中裂缝的延伸距离分别为0.3、0.4、0.6 m和无限长,在图11中裂缝的延伸距离分别为0.3、0.4、0.5、0.6 m和无限长。发现透射纵波和透射斯通利波的波形受裂缝的延伸距离影响不明显,而透射横波的幅度和相位随着裂缝延伸距离的改变而发生了明显变化。当裂缝的延伸距离为0.3 m时,横波的衰减也很小,透射横波的幅度较大。随着裂缝延伸距离增加,透射横波首波的幅度减小、波峰右移。当裂缝的延伸距离为0.6 m时,透射横波首波的波峰突然左移到无限长裂缝情况下的波峰附近,并且透射横波首波的幅度也与无限长裂缝情况下的幅度相近。

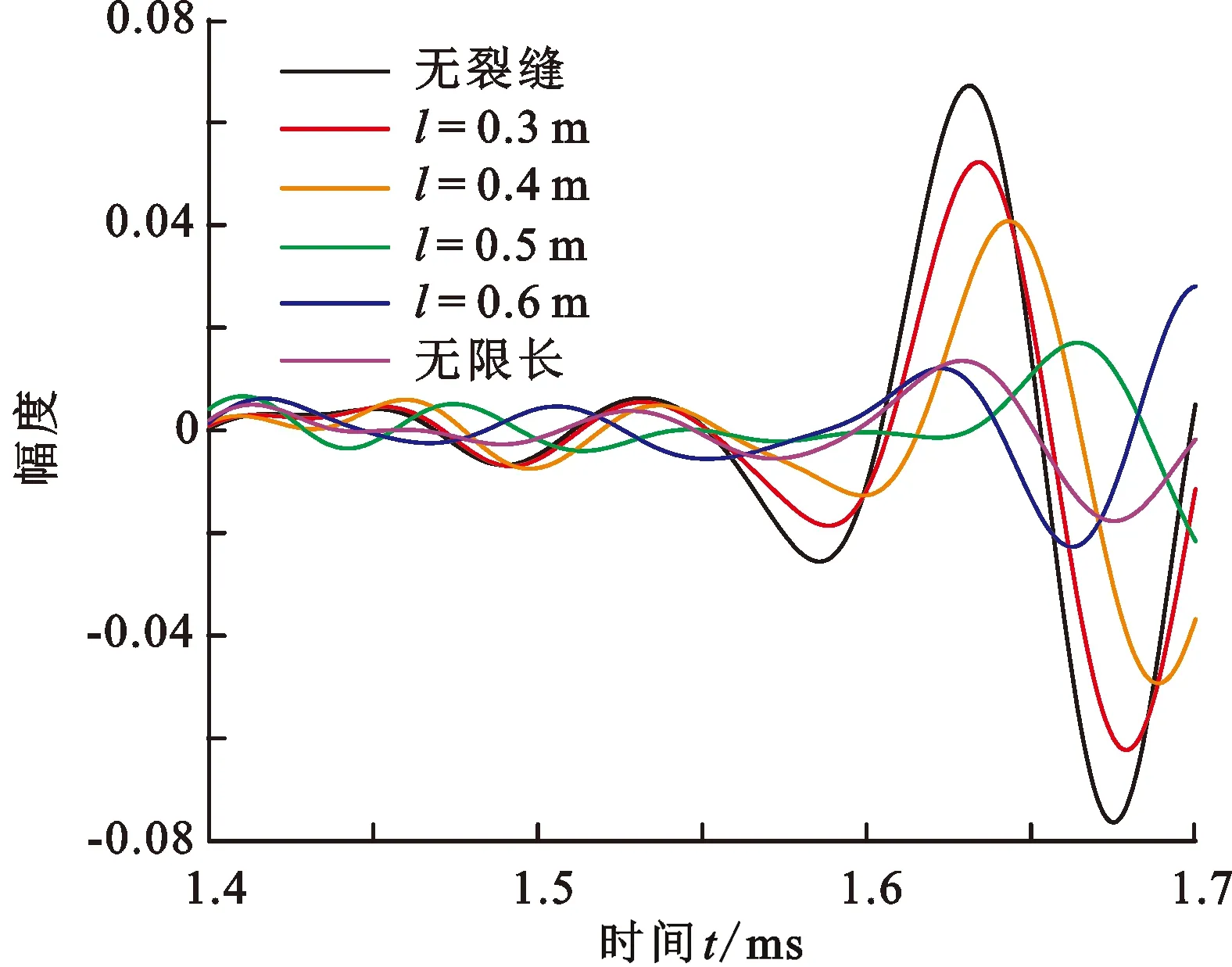
图11 不同裂缝延伸距离情况下透射横波首波的波形Fig.11 Waveforms of transmitted shear head waves with different extended distances of fractures

3.3 多条裂缝模型

模拟井中声波在多条裂缝模型中传播,研究不同裂缝条数对声波波形的影响。图12为不同裂缝条数情况下的透射声波波形,接收器的源距为3 m。模型中裂缝的条数分别为2、4和6,每条裂缝的宽度为1 mm。如图12所示,随着裂缝条数的增加,透射纵波的波形变化不大,透射横波和透射斯通利波的幅度减小,其中斯通利波幅度的衰减非常明显。观察横波首波可以发现,由于裂缝带的宽度随着裂缝条数的增加而增加,多条裂缝模型使透射横波的相位发生了很大变化;不同裂缝条数对应的相位不同。

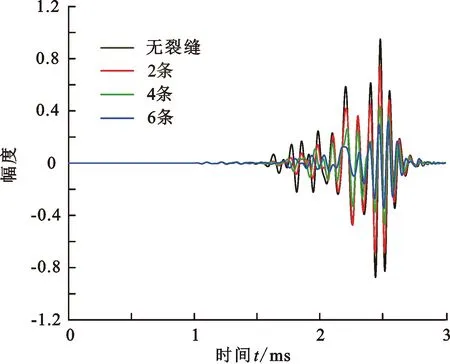
图12 不同裂缝条数情况下的透射声波波形Fig.12 Waveforms of transmitted acoustic wave with different fracture numbers

4 结 论

(1)裂缝对纵波的影响很小,距离裂缝较远的纵波波形几乎没有改变;由于狭窄的裂缝对声波的散射作用,靠近裂缝的透射纵波受到散射波的干扰,波的幅度发生了改变;裂缝的宽度越大,散射波对透射纵波幅度影响越大。

(2)横波对裂缝非常敏感,裂缝不仅对横波有很强的衰减和反射作用,而且使横波的相位发生了改变;距离裂缝越远,横波的衰减程度越高;不同宽度裂缝对应的横波幅度变化很小;当裂缝的延伸距离很短时,随着裂缝延伸距离增加,透射横波首波的幅度减小,波峰右移;对于多条裂缝,随着裂缝条数的增加,透射横波的幅度减小,横波的相位也发生了很大变化。

(3)裂缝也会引起斯通利波很强的衰减和反射;斯通利波对线性滑动理论所描述的裂缝宽度的变化不是很敏感,随着裂缝宽度的增加,斯通利波幅度的衰减增加不明显,因此在线性滑动模型中,不适合用斯通利波定量评价裂缝宽度;对于多条裂缝,随着裂缝条数的增加,透射斯通利波的幅度明显减小。