单轴旋转SINS惯性系对准方法研究

常振军，张志利，周召发，陈 河2，赵军阳

(1.火箭军工程大学 兵器发射理论与技术国家重点学科实验室，西安 710025；2.火箭军研究院，北京 100085)

0 引言

捷联惯导系统(strapdown inertial navigation system，SINS)初始对准为陆基车载导航提供初始条件，对准时间和精度直接影响导航系统的工作性能[1-2]。初始对准通常分为粗对准和精对准两个阶段，其中粗对准获取粗略姿态矩阵，在此基础上，利用小失准角误差模型完成滤波精对准或者针对大失准角开展非线性滤波完成精对准[3-4]。传统的解析法对准利用重力加速度和地球自转角速度双矢量定姿获取粗略姿态，但地球自转角速度很容易被晃动干扰角速度淹没。为解决晃动基座干扰的问题，多采用基于惯性凝固坐标系分解的思想，利用不同时刻惯性系下重力矢量不共线，通过双矢量定姿[5-6]或者将其转化为wahba问题进行多矢量定姿求解姿态矩阵[7-8]，可以隔离晃动角速度干扰，克服晃动基座对初始对准的影响。进一步地，通过低通滤波等提高抗线振动干扰能力，取得较好的效果。利用惯性系对准方法，还可以通过引入测速设备可完成行进间初始对准[5-6]。另外，为了抑制惯性器件等效常值误差影响，并且提高系统可观测性，可采用多位置或者旋转基座实现初始对准，其中连续旋转能够更好地提高系统可观测性及对准精度[9-10]。但对多位置及旋转调制初始对准方法的研究，多集中于解析式对准或双矢量定姿对准中，对旋转调制多矢量定姿的研究甚少。

本文在阐述单轴旋转调制误差抑制及惯性系双矢量定姿和多矢量定姿原理的基础上，将两者结合应用于捷联惯导静基座初始对准中，对比分析单位置对准和连续旋转对准、双矢量对准和多矢量对准的对准精度，最后进行仿真及设备实验验证。

1 单轴旋转调制误差抑制原理

在静基座条件下，由初始对准极限误差分析可知，其对准精度主要受水平惯性器件等效误差影响。相比于单位置初始对准，单轴旋转调制方法将惯性测量单元IMU(inertial measurement unit)相对载体绕方位轴按固定角速度连续旋转，能够使系统变为完全可观，并且可将水平惯性器件的常值误差调制为周期信号，该信号在固定的旋转周期内积分为零，从而抑制水平惯性器件常值误差对初始对准结果的影响。

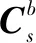
(1)

则旋转后载体坐标系下的陀螺仪和加速度计输出为：

(2)

(3)

由公式(2)～(3)可知，水平惯性器件的常值误差经过单轴旋转调制后变为周期信号，且在一个旋转周期内积分为零。由于初始对准误差主要与水平惯性器件常值误差相关，所以经过旋转调制可以达到抑制误差的效果。

2 惯性系初始对准

2.1 惯性系双矢量定姿

为阐述惯性系初始对准算法，对本文涉及的坐标系做如下定义：

1)地心惯性坐标系(i系)：原点设在地心，oixi轴在赤道平面内指向春分点，oiyi轴指向地球自转轴方向，向北为正，oizi轴与前两者构成右手直角坐标系；

2)地球坐标系(e系)，原点在地心，oexe轴在赤道平面内指向起始子午线，oeze轴平行于地球自转轴方向，向北为正，oeye轴与前两者构成右手直角坐标系；

3)地理坐标系(n系)，选取“东-北-天”坐标系，设为导航坐标系；

4)载体坐标系(b系)，选取“右-前-上”坐标系；

5)初始时刻惯性坐标系(i0系)，在初始对准起始时刻，原点与载体系原点重合，oi0xi0轴平行于赤道平面指向当地子午面，oi0zi0轴平行于地球自转轴方向，向北为正，oi0yi0轴与前两者构成右手直角坐标系，三轴在惯性空间内指向不变；

6)初始时刻载体惯性坐标系(b0系)，将初始时刻的载体坐标系(b系)凝固到惯性空间，在初始对准过程中三轴不随载体转动，相对于惯性空间指向不变。

另外，设地球自转角速度为ωie，重力加速度为g，当地地理纬度为L。

2.2 惯性系双矢量定姿

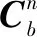
(4)

(5)

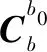
(6)

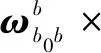
(7)

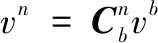
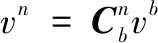
(8)

(9)

(10)

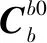
为了降低加速度计测量过程中外界干扰带来的影响，可对公式两边同时取一次积分，得到：

(11)

由于重力矢量相对地心惯性坐标系随着地球转动而连续缓慢移动，在惯性空间内运动轨迹是一个以地球自转轴为旋转轴的锥面，所以不同时刻的重力矢量均不共线。在初始时刻惯性坐标系和初始时刻载体惯性坐标系中，取不同时刻的重力矢量，利用公式(11)，通过双矢量定姿算法可确定两个惯性坐标系之间的转换矩阵：

(12)

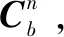
2.3 惯性系多矢量定姿

设有s个(s>2)不共面的量测矢量，根据其在两个坐标系内的分别投影可求解两个坐标系之间的转换矩阵，即多矢量定姿算法。考虑利用量测矢量确定载体姿态的问题为Wahba问题，其本质是带约束条件的最小二乘问题[11-12]，可构建目标损失函数：

(13)

由于gb0和gi0均随时间连续变化，Vb0和Ui0也随时间连续变化，可将公式(13)写成积分形式，通过求取最优姿态矩阵的估计值使得目标损失函数最小：

(14)

1968年，Davenport提出q-method算法，将利用量测矢量确定载体姿态的Wahba问题转换为求解所构造的四阶对称矩阵特征向量，以四元数形式给出最优解[13]。四阶对称矩阵构造方法为：

(15)

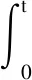
(16)

相比双矢量定姿算法，多矢量定姿初始对准充分利用了每个时刻测量的重力矢量，提高了测量信息使用率，并达到了最小二乘意义的最优解，可以增加抗随机突变和干扰的能力，从而提高初始对准性能。

3 实验验证与分析

本节通过仿真及实验验证前文理论分析。仿真条件设置如下：对准地点地理纬度设置为北纬34.25°；3个陀螺仪常值漂移为0.01°/h，角随机游走系数为0.001°/h1/2，加速计常值零偏为50 μg，随机游走系数为5 μg/Hz1/2。载体初始俯仰角θ=0°，横滚角γ=0°，航向角ψ=50°。对准时间共600 s，系统采样频率100 Hz。其中，单轴旋转方案设为绕方位轴以角速度18°/s进行旋转，转动时间从初始时刻连续转动至540 s，而后停留在转动起始位置，转动过程中忽略转动误差影响。

3.1 单位置与单轴旋转调制初始对准仿真对比

为了分析单轴旋转调制的效果，验证前文理论分析，采取的仿真试验步骤为：由轨迹模拟器及惯性器件信息分别生成静基座单位置和单轴连续旋转调制两种工况下的仿真实验数据；为便于对比分析，同样采用惯性系多矢量定姿对准方法，对两种工况进行初始对准，仿真结果如图1～3所示。

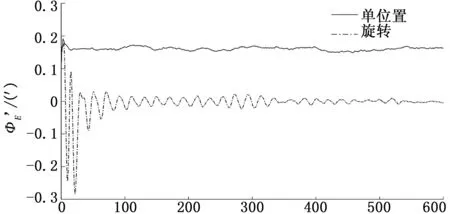
图1 东向失准角对准仿真结果(单位置与旋转调制)

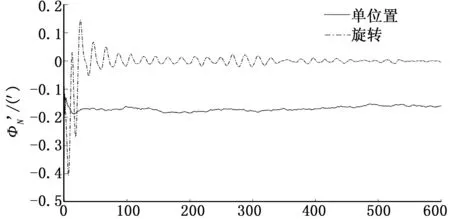
图2 北向失准角对准结果(单位置与旋转调制)

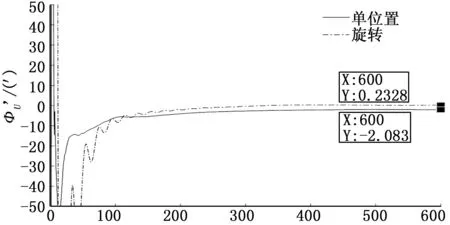
图3 方位失准角对准仿真结果(单位置与旋转调制)

由图1～3仿真结果可看出，与静基座单位置初始对准相比，绕方位轴连续旋转调制的初始对准方法提高了系统的可观测性，东向和北向失准角得到了有效估计，并且由于转动周期内抑制了水平惯性器件的常值误差，方位对准精度得到了明显提高。

3.2 双矢量与多矢量定姿初始对准对比

为了对比分析惯性系双矢量定姿与多矢量定姿的对准性能，首先进行仿真验证，采取的仿真试验步骤为：同样利用单轴连续旋转调制的实验数据，分别采用双矢量定姿和多矢量定姿进行初始对准，转动方案同前文，由于水平姿态角误差较小，仅对方位失准角进行对比仿真验证分析，方位失准角对准结果如图4所示。

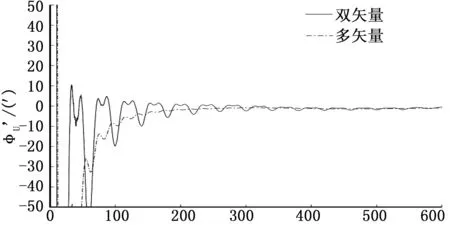
图4 方位失准角对准仿真结果(双矢量与多矢量)

由图4仿真结果可知，在单轴连续调制的工况下，相比于惯性系多矢量对准，惯性系双矢量初始对准的方位失准角曲线存在较大波动，收敛速度较慢，验证了前文对于惯性系双矢量对准测量矢量利用率不高，测量矢量的误差对初始对准结果影响较大的分析。若晃动干扰幅度较大，对准误差将更加明显。而由于惯性系多矢量对准充分利用对准过程中的量测矢量信息，达到了最小二乘意义下的最优解，对准性能相比惯性系双矢量对准算法得到明显提高。

为进一步验证上述关于惯性系双矢量与多矢量对准性能的分析，利用内置双轴旋转式激光捷联惯组进行单位置对准实验验证。对准时间共300秒，采样频率为100 Hz；3个激光陀螺零偏分别为0.0050°/h、0.0048°/h、0.0045°/h，随机游走系数分别为0.00046°/h1/2、0.00044°/h1/2、0.00047°/h1/2；加速度计零偏分别为47 μg、51 μg、37 μg，随机游走系数为5 μg/Hz1/2。以高精度摆式陀螺经纬仪寻北得到的实际方位角值作为对比基准，将惯性系双矢量对准和多矢量对准得到的方位角对准结果与基准方位角对比得到各自的方位失准角。局部放大的实验结果数据曲线见图5。

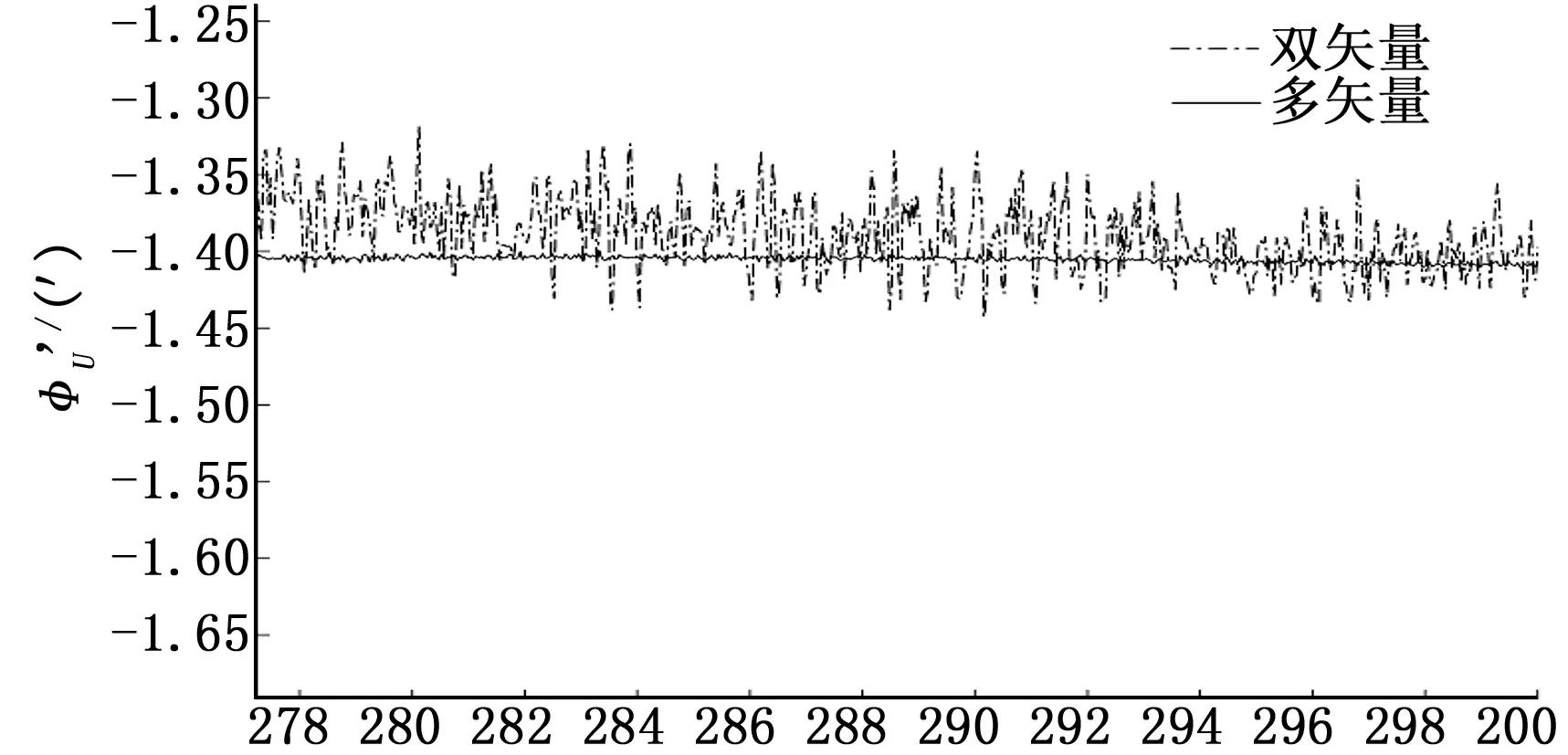
图5 方位失准角对准实验结果(双矢量与多矢量)

由图5实验结果可见，惯性系双矢量对准由于只利用了两个时刻的量测矢量，对准精度更容易受到所测时刻量测信息误差的影响，对准曲线波动较大，方位失准角方差较大，抗干扰能力和对准性能不如惯性系多矢量对准方法，验证了前文分析结论。

4 结论

本文通过对单轴连续旋转调制捷联惯导初始对准的误差抑制原理进行分析，利用惯性凝固坐标系分解的思想，建立惯性系双矢量定姿和多矢量定姿的初始对准模型，对比分析了两种惯性系对准方法的特点，结合单轴旋转调制和惯性系多矢量对准实现初始对准，并进行了仿真及设备实验验证。结果表明，相比单位置对准，单轴连续旋转调制能够有效抑制水平惯性器件误差影响，提高失准角对准精度；相比于惯性系双矢量对准方法，惯性系多矢量对准能够更加充分利用测量矢量信息，抑制外界干扰，提高对准性能。