水冷壁爬壁机器人路径跟踪研究

(常州大学 机械工程学院，江苏 常州 213100)

0 引言

流化床锅炉水冷壁的磨损是锅炉的主要失效形式之一[1-2]，为保证锅炉运行安全，需要定期检测水冷壁的磨损程度。由于人工作业效率低且安全性系数低，因此研制一种能自主检测水冷壁磨损的爬壁机器人是现在化工行业所急需的。

保证水冷壁爬壁机器人准确按照期望的直线路径运动是其研究的前提，所以对其路径跟踪的研究是必不可少的。针对路径跟踪这类问题，相关学者进行了大量研究并提出了各自的解决方案。蒋建东[3]等提出了模糊控制的方法，但模糊控制需要根据专家经验建立模糊规则，若不能建立理想的模糊规则，将影响其控制效果。张扬名[4]等基于滑模控制方法来实现路径跟踪控制，但由于滑模控制方法的特性使其存在“抖振”，且无法避免，实际控制效果不理想。

针对上述问题，基于水冷壁爬壁机器人的运动学模型，利用Back-stepping跟踪算法设计了一种水冷壁爬壁机器人路径跟踪控制律，同时采用Lyapunov稳定理论对路径跟踪控制律的收敛性进行验证，通过对机器人速度大小的控制以及选择合适的参数，保证其运动的稳定性。通过MATLAB软件进行仿真实验，实验结果验证了该方法鲁棒性好，自适应能力强。

1 水冷壁爬壁机器人结构

为了使水冷壁爬壁机器人能够完成磨损检测任务，水冷壁爬壁机器人需具备三个基本功能：吸附、运动和磨损检测功能。本实验研究的爬壁机器人采用永磁体吸附的吸附方式和履带式移动的移动方式。

如图1所示是水冷壁爬壁机器人的工作环境水冷管壁图。水冷壁是由钢制的水冷管焊接形成的密排管壁，锅炉内燃烧形成的飞灰颗粒的高速冲刷会对水冷壁造成磨损，所以需要定期检测其受磨损程度。

图1 水冷管壁图

图2所示是水冷壁爬壁机器人三维图，其本体由驱动机构,永磁吸附机构,超声波无损检测机构等组成。爬壁机器人通过装有特制永磁铁的履带紧紧地吸附在水冷壁壁面，驱动电机通过蜗轮蜗杆减速器带动链轮,链轮与链条啮合,从而使机器人沿着水冷管壁运动。

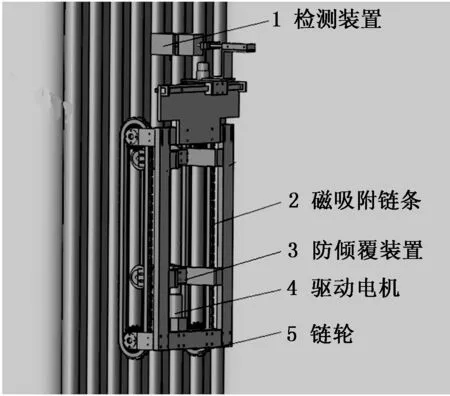
图2 水冷壁爬壁机器人三维图

水冷壁爬壁机器人由左右两侧的驱动电机提供驱动力，由于电机本身的制造差异，导致两侧履带的速度不可能完全一致，致使机器人偏离期望路径[5]，从而影响了测量结果的可靠性。所以需要对爬壁机器人的路径识别及跟踪进行研究，动态地控制机器人的运行轨迹为期望的直线路径，保证磨损检测结果正确。

2 水冷壁爬壁机器人运动模型

根据水冷壁爬壁机器人机械结构与工作环境，为建立其空间运动模型，对爬壁机器人作出如下假设[6]：

1)在二维平面内运动；

2)爬壁机器人为刚体；

3)两侧履带完全一致，且中心线与运动方向垂直。

在以上假设的情况下，如图3所示，在XOY参考面上，点c(xc,yc)为机器人质心坐标，θ为机器人运动方向与参考坐标系x轴正向夹角，那么爬壁机器人的位姿可用P=[xc,yc,θ]T来表示，再选择目标参考点k(xk,yk)，d为机器人质心c与目标参考点k的距离，α为直线CK与机器人坐标系y轴的正向夹角。

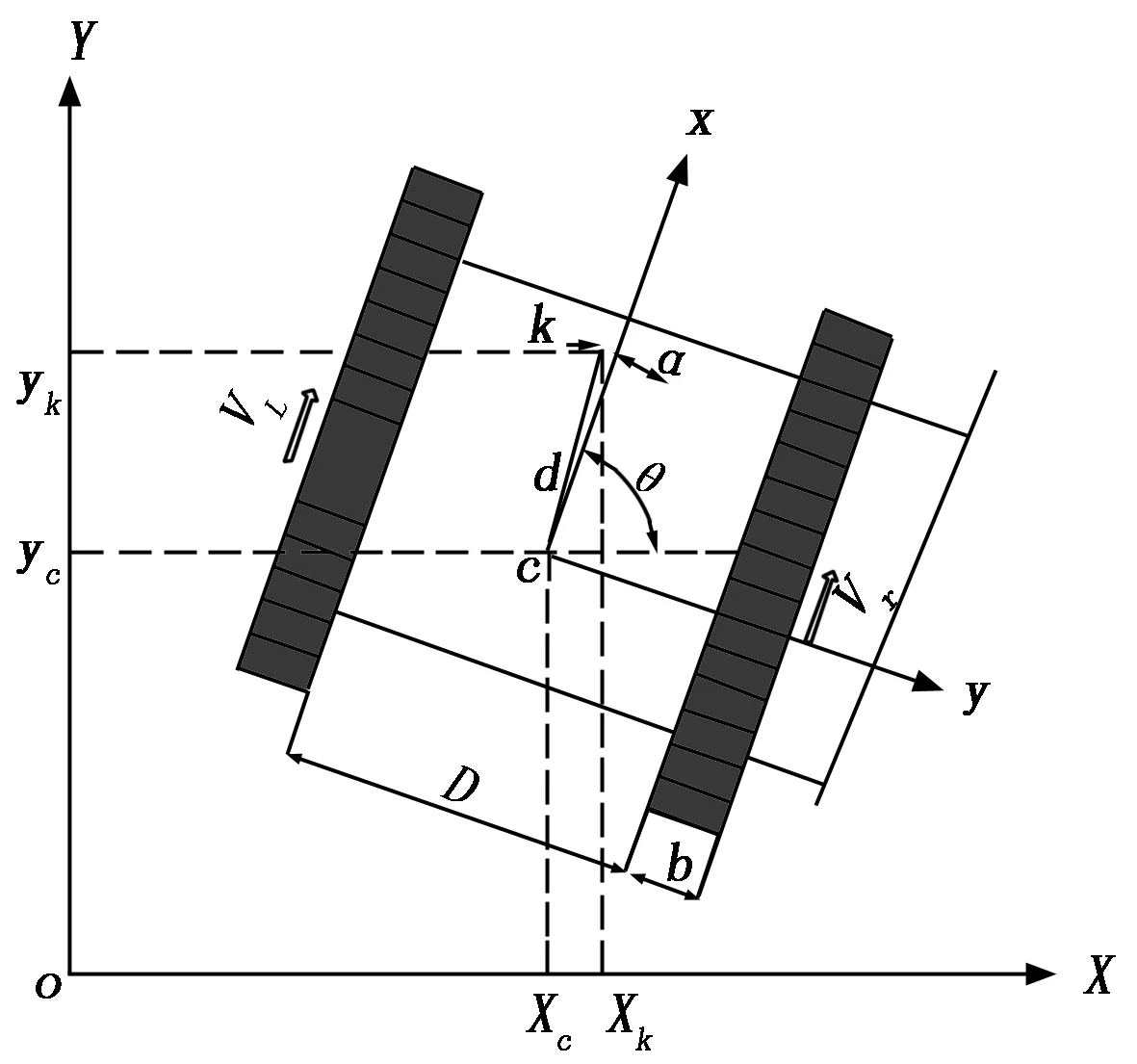
图3 爬壁机器人运动示意图

由图3可得：

(1)

对式(1)中的时间t求导可得：

(2)

设左右履带理论速度分别为vL和vR，则：

(3)

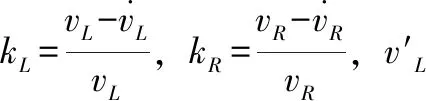
水冷壁爬壁机器人在实际工作过程中几乎不发生滑动的情况，可以将式(3)改写成下式：

(4)

结合式(12)和(14)可得：

(5)

当点K取为点C时，爬壁机器人的运动学方程可写成如下：

(6)

其中:P表示爬壁机器人的位姿矩阵。

则爬壁机器人质心C处的速度可按下式表示：

(7)

即：

(8)

结合式(6)和(8)，水冷壁爬壁机器人的运动学方程也可以表示为：

(9)

3 水冷壁爬壁机器人路径识别及跟踪控制

根据上章得出的机器人空间位姿方程，本章通过对实时图像的处理获得爬壁机器人实际空间运动轨迹，利用Backstepping跟踪算法设计了一种通过调控速度控制位姿的路径跟踪控制律，从而实现对爬壁机器人的直线路径跟踪。

3.1 水冷壁爬壁机器人路径识别

水冷壁爬壁机器人使用平行于水冷壁安装的摄像机实时拍摄水冷管壁图像，并进行图像处理，提取直线路径，实现对爬壁机器人位姿的实时反馈。如图4所示为摄像机定位图，其中AB为摄像机图像成像平面。

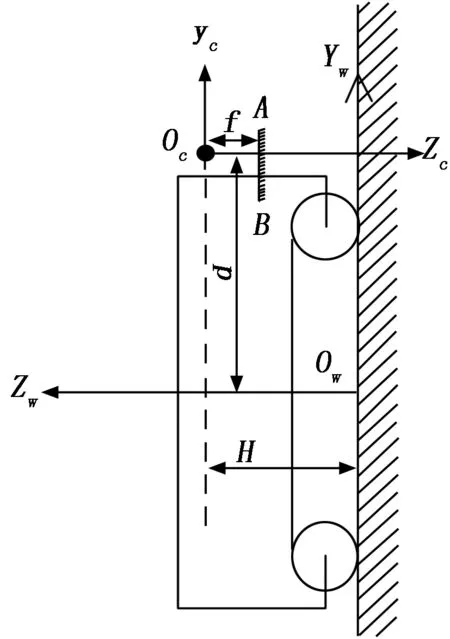
图4 摄像机定位图

对图像的预处理首先将图像灰度化，然后利用高斯滤波及图像二值化对图像进行预处理。图像预处理流程图如图5所示。

图5 图像预处理流程图

将图像预处理以后，通过Hough变换[7]来获取图像导航参数，提取直线路径。

利用函数cvHoughLines2()在经过预处理的图像中识别出两条边界线，当两条边界线被检测到之后，再利用OpenCV中的cvLine()函数提取其中心线，则提取的初始中心线即为爬壁机器人的期望直线路径。

水冷管壁图像处理如图6所示。其中(a)为对水冷管壁图像灰度处理；(b)为进一步的滤波处理；(c)为二值化处理；(d)为边缘检测处理；(e)为Hough检测处理;(f)为最后的直线路径提取。

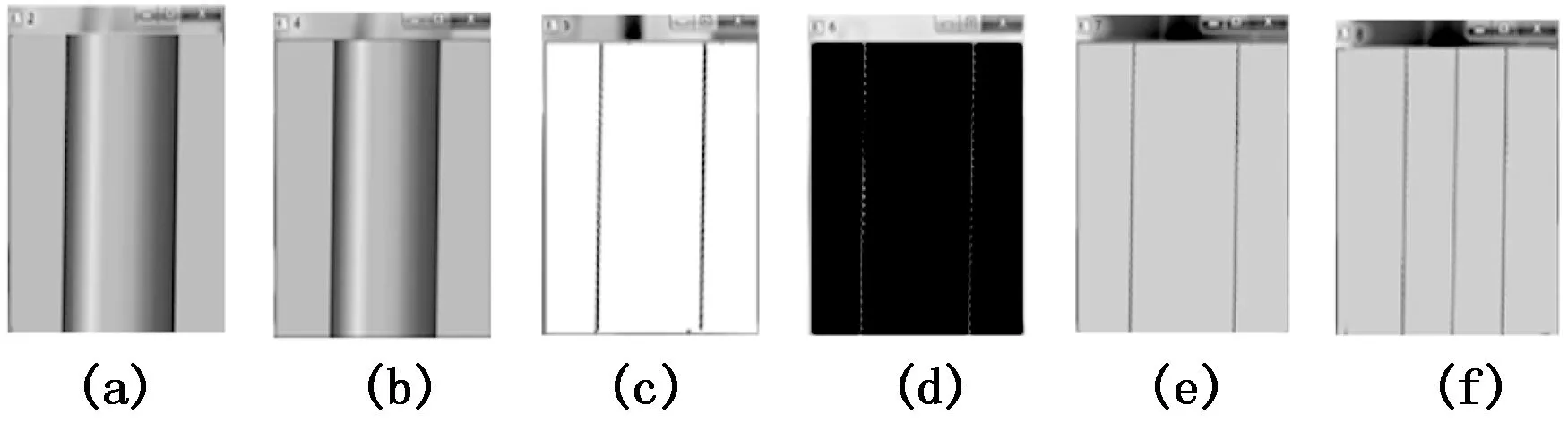
图6 水冷管壁图像处理图

3.2 水冷壁爬壁机器人路径跟踪控制

本文水冷壁爬壁机器人路径跟踪控制律的设计在提取期望直线路径的基础上，根据反向递推跟踪算法和Lyapunov稳定理论设计一种控制律U=[vLvR]T，使爬壁机器人的路径跟踪在全局渐近稳定。

爬壁机器人位姿误差示意图如图7所示。

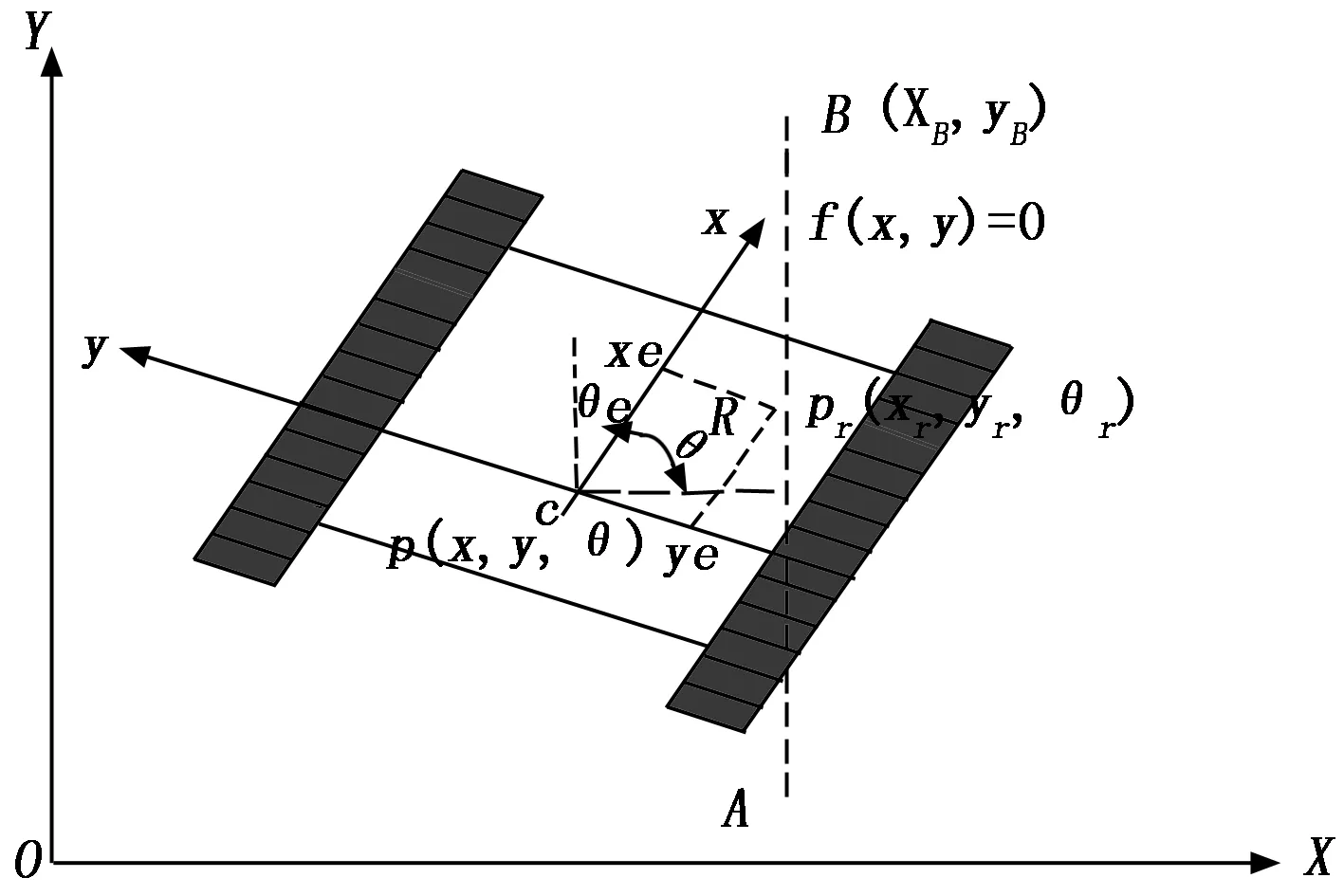
图7 爬壁机器人位姿误差示意图

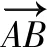
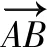
在爬壁机器人自身局部坐标系xcy下，其实际位姿和参考位姿之间的误差，即局部位姿误差Pe，通过以下坐标变换：

(10)

可得到局部位姿误差：

(11)

其中:Re为变换矩阵。

由式(11)可进而得出爬壁机器人的位姿误差微分方程[8]为：

(12)

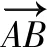
图8 爬壁机器人位姿控制流程图

根据引理1[9]：对于任意x(x∈R)且满足|x|<∞，有φ(x)=xsin(tan-1x)≥0，当且仅当x=0时等号成立。

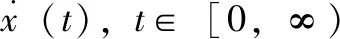
由Lypunov稳定性理论，设系统的状态方程为：

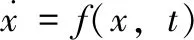
(13)

其平衡状态为：

f(0,t)=0(t≥t0)

(14)

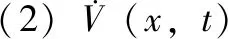
(15)

由此构造Lyapunov函数：

(16)

根据式(16)可得，V≥0，当且仅当[xeyeθe]T=0时，V=0。

对式(15)求导可得：

(17)

再对式(16)进行求导，则：

k1sin(tan-1(ω))(-ωxe+vrsinθe))-

(18)

设t∈[0,+∞)，vr和ωr都有界且不同时为0，则根据式(18)控制律可取为：

(19)

式(19)是根据Lyapunov构造的函数设计的控制律，将其结合式(12)得到相关微分方程：

(20)

再把控制律(19)代入(18)，整理可得：

(21)

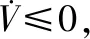
综上所述，利用Lyapunov函数设计的控制律使pe有界，即：

(22)

4 实验仿真与分析

通过MATLAB软件[12]对所设计的路径跟踪控制律进行模拟仿真实验。

参考轨迹取为直线，假设机器人的初始位姿PA=(-0.3 0.25π/12)，参考轨迹初始位姿PB=(0.1,π/4)，期望速度为vr=0.4 m/s，ωr=0，取参数k1=1，k2=3.5，k3=3.5，经过多次实验后，仿真结果如图9所示。仿真中直线路径跟踪的位姿误差如图10所示。

图9 直线跟踪仿真

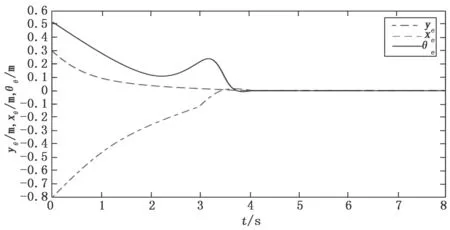
图10 直线跟踪仿真的位姿误差

由仿真结果可以看出，在所设计的控制律下，水冷壁爬壁机器人能渐近跟踪给定的参考轨迹，并在短时间内达到稳定，验证了该控制律的可靠性。

5 结论

本文通过摄像机采集水冷管壁图像，对图像的处理并提取导航信息参数，实现了对水冷壁爬壁机器人直线路径的提取，再利用Backstepping跟踪算法和Lyapunov稳定理论设计了一种水冷壁爬壁机器人路径跟踪控制律，并利用Matlab软件进行了模拟仿真实验，通过仿真结果可知该路径跟踪控制律合理可靠，具有较高的应用价值。