自适应算法在漆包线漆膜连续性检测中的应用
2019-06-27陈东泽李尤鹏贺慧勇
陈东泽,李尤鹏,贺慧勇
(长沙理工大学物理与电子科学学院,长沙410114)
0 引言
随着现代检测技术的飞速发展和处理器速度不断的提高,LMS 自适应时延估计算法成为了信号分析与处理领域一个重大研究课题,它被广泛应用于流速测量、管道泄漏检测、目标跟踪定位等领域中。不过大部分研究者多侧重LMS 自适应时延算法理论的改进以及优化,目前还没有研究者将算法应用于漆包线漆膜连续性检测当中。
漆包线漆膜检测传统方法包括日本盐水法、低压水银法、激光法测直径、压轮式直流高压漆膜连续性检测法等。日本水银法需要人工观察记录,检测能力有限。低压水银法一般只适用于Φ0.5mm 以下的漆包线,并且水银的渗透性会影响漆包线漆膜缺陷检测的严格性和准确性,并且水银是有毒物质。激光法测直径对关键件的要求很高,关键件误差较大会影响其检测精度。压轮式直流高压漆膜连续性检测法对技术要求过高。但是利用LMS 自适应时延算法可以通过利用缺陷信号在时延上存在相关性而噪声信号不存在相关性的特点来有效的提取出缺陷信号,能够有效解决传统方法一路检测漏检误检等问题,自适应滤波器是一种能够自动调节本身的滤波器参数已达到某种最佳的统计准则要求的滤波器,它的突出特点是并不需要预先预知输入信号和噪声特性。自适应算法常用的准则有LMS(最小均方误差)准则。LMS 自适应时延算法原理是自适应算法的应用,其原理是采用参数模型法设计滤波器的冲击响应函数,通过LMS 自适应来迭代调整冲击响应函数对称轴的位置来拟合两路信号时延的大小。这种方法实质将自适应算法转换成一个滤波器的设计和实现问题,通过不断的迭代和求逆实现滤波器的设计,当滤波器的权参数趋于稳定后,此时均方误差刚好趋于一个最小值,那么权参数最大值处对应的延时点即是我们所要求的延时点。但通过大量的现场漆包线数据分析之后,发现漆包线信号数据量非常的庞大,并且大部分并不是我们需要关心的缺陷信号,如果直接全部做自适应时延运算会影响处理的速度,故验证LMS 自适应时延算法在漆包线漆膜检测的可行性以及算法的优化是本文的核心。
1 漆包线自适应时延算法检测的原理
具体漆包线信号采集过程是通过两路红外对管(红外对管包括红外发射管和红外接收管)采集漆包线的反射光强度并通过后级的调理电路将光信号转换成电信号放大至0-5V 的电压来提取出漆包线信号。具体实验中红外对管中红外发射管和红外接收管的间距为3mm,红外对管1 和红外对管2 是同型号的产品,两个红外对管之间的距离为5cm,整个系统图如图1。为了保证数据传输的准确性,我们还采用虚拟示波器和处理器同时采集数据以确保数据的准确性。

图1 漆包线自适应时延检测算法原理
后级的信号处理采用的是自适应时延算法处理,因为在漆包线运动过程中,通过漆包线连续性检测平台采集的数据中缺陷信号淹没在强大的噪声信号中,所以通过缺陷信号在通过两路对管的时候具有延时性而噪声信号不具备这特性来提取缺陷信号,但在处理的过程中发现由于采集的数据量过大,而且大部分数据不是所需要的缺陷信号。所以在进行自适应时延估计算法处理前需要前级简化筛选算法处理,先设定两路漆包线信号的数据的阈值,然后通过阈值先初步筛选掉大量的无用漆包线信号。
在两路红外对管之间的距离和漆包线测量平台运动线速度已知的情况下,理论的延时值就可以通过计算得到。与此同时,自适应计算延时的结果主要受采样频率以及计算窗口的大小有关。根据采样定理决定了采样频率应该足够高,计算窗口代表的时间必须大于两路信号的渡越时间。在满足这些条件下,假设经过前级预处理的两路红外对管信号为X1(n)和X2(n),设定W(n)为自适应滤波器的加权系数,分别取X1(n)和X2(n)的n 个点的数据并将这两路信号送入自适应滤波器,进行如下的运算:

进而得到均方误差:
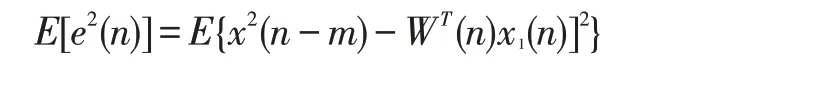
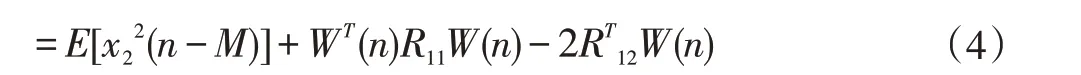
具体计算过程如图2 所示。

图2 漆包线漆膜连续性检测自适应延时算法的流程图
根据漆包线检测平台的红外对管之间的距离,漆包线运动的线速度以及漆包线数据的采样率来确定合适迭代步长因子u 满足收敛条件以及M 的值,经过权参数的多次迭代,当权参数趋于稳定后,即上述均方误差趋于最小值时,此时自适应滤波器必将收敛于维纳滤波器。此时权矢量峰值对应的时间点即是该段时间对应的两路信号的时间延时,将此时间延时值记录下来与理论的时间延时值进行对比,如果相差太大,就可以证明该段信号不是缺陷信号,如果两个值相差不大,则可判定可能是缺陷信号。进行完上述的计算后,将数据自动推后z 个点(z<n),同样进行上述的漆包线自适应算法的处理,如果连续几个自适应窗口时延值都与实际值相差不大则判定该处必定有缺陷信号。
2 漆包线采集数据对算法的验证
在满足这些条件下,对得到的漆包线数据进行处理,样本数据一现场的漆包线直径为Φ1.0,漆包线长度为1077m,数据采样率为32kHz,静止状态下漆包线红外对管之间的距离为5cm,漆包线线速度为235m/min,样本数据二现场的漆包线直径为Φ1.0,漆包线长度为1070m,数据采样率为16kHz,静止状态下漆包线红外对管之间的距离为5cm,漆包线线速度为235m/min。
在上述筛选算法处理的基础上,对筛选后的漆包线数据进行自适应时延算法处理,由上面数据可以可知样本数据一的采样率为32k,线速度为235m/min,红外对管间距为5cm,理论延时值为12.77ms(对应32k 采样率对应的点数为408)。对现场的漆包线观察时可以发现该组漆包线在963m 处左右有缺陷,于是对该处数据进行处理时,先取1024 个点窗口数据自适应步长U=0.04,M=500(M>408),对其进行处理,可以发现窗口内除了408 处有峰值外还有几个伪峰值,甚至比所求的峰值的幅度还高如图3 所示,由于漆包线前级电路已经对漆包线数据进行了前级滤波,故该噪声很有可能后级处理AD 采样时产生的,故我们在对数据处理前在对数据进行再滤波,于是在加了滤波器后,所需要的峰值就明显可见了。如图4,所以前级的再滤波可以凸显时延峰值。
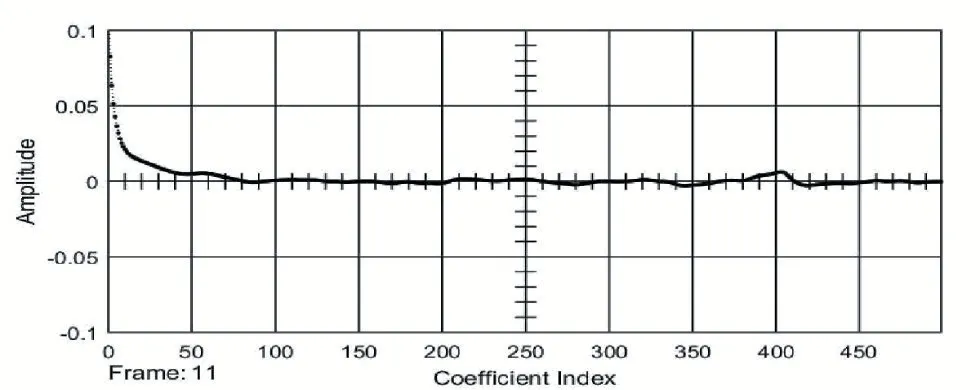
图3 没加滤波器数据一的时延图

图4 加了滤波器数据一的时延图
对样本数据一漆包线数据进行自适应时延处理,可以通过上述的计算得到自适应理论延时点数为408,转化成时间为12.77ms,其中设定自适应步长u=0.04,M分别是250,500,1000,计算自适应时延值。当M=250时,延时点数无法计算;当M=500 时,延时点数为405,转化成时间为12.65ms;当M=1000 时,延时点数为405,转换时间为12.65ms;
对样本数据三漆包线数据进行自适应时延处理,采样率为16k,故计算得到的理论延时点数为204,转化成时间为12.65ms,其中设定自适应步长仍为u=0.04,M=300,在266m 缺陷处可以得到实际处理得到的时延值为201,转化成时间为12.56ms。时延图如图5。

图5 16kHz自适应时延图
从上述数据以及时延图可以看出在漆包线采集过程中存在相关噪声,在进行自适应时延处理前需进行前级再滤波处理;自适应滤波器长度M 的值太小的话无法估测出时延值,但是M 的值选的过大的话可由自适应时延算法原理知会导致自适应算法的收敛速度变慢[8];通过对比样本数据一三可以看出两组数据在只有采样率不同的情况下,采样率小的话,相对应的自适应时延滤波器阶数M 可以相对取小些,这样可以收敛速度变快些。
3 结语
本文从漆包线漆膜连续性缺陷出发,介绍了红外接收管采集漆包线漆膜连续性信号的实验装置和自适应时延检测漆包线缺陷的原理,在对漆包线数据进行了前级简化和滤波处理后,验证了漆包线自适应时延检测的可行性。对比了同一采样率和线速度下自适应滤波器阶数M 值对计算结果的影响。同时对比了不同的采样率对M 值选取的影响。由微弱信号处理中自适应算法原理可以知道选取过大的自适应滤波器阶数M,会使得迭代次数变长,收敛速度变慢[8],故选取过大M 会使时延计算速度变慢,选取过小的自适应滤波器阶数M,则无法计算出时延值。并且采样率越小,可以发现M 值可以相对选取小些。因此需要根据采样率和实际需求来确定自适应滤波器的阶数M。
