图形万变不离其宗
2019-06-26毛巾钧
毛巾钧
“图形的变化”这一知识点是初中几何的重要内容,主要包括图形的平移、旋转和轴对称等。下面整理了几种典型错例并予以剖析,希望对同学们有所帮助。
一、概念不清
例1在矩形纸片ABCD中,AB=3,BC=2,沿对角线AC剪开(如图1)。固定△ADC,把△ABC沿AD方向平移(如图2),当两个三角形重叠部分的面积最大时,平移的距离AA′等于( )。
A.1 B.1.5 C.2 D.0.8或1.2
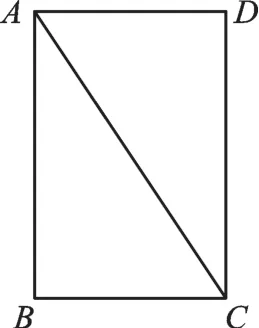
图1
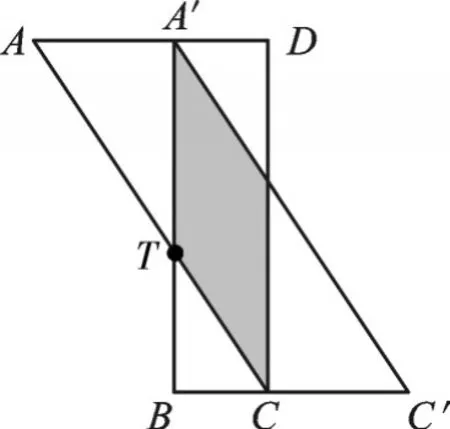
图2
【错解】D。
【错因】本题是平移背景下二次函数的最值问题。很多同学往往只停留在直观的感受层面,难以从平移的定义和性质出发进行推理和计算。
【正解】本题根据平移的性质得到平行,进而得出三角形相似,同时得到重叠部分为平行四边形。如图2,设A′B与AC的交点为T,即有△AA′T∽△ADC。设平移的距离AA′=x,根据相似得,再利用平行四边形面积公式,得出重叠部分的面积·(2-x),求此二次函数取最大值时的x值即可。
正确答案:A。
二、性质不明
例2如图3,在正方形ABCD中,已知P为边AD的中点,Q为边BC上一点,且把这个正方形折叠,使得P、Q重合,折痕为MN,则

图3
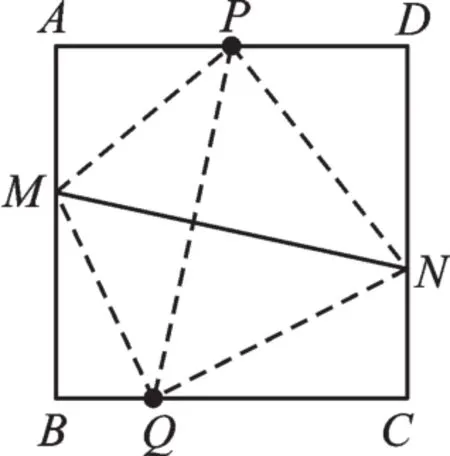
图4
【错解】。
【错因】不会分析“折叠”,难以联想到折叠的性质——对称轴垂直平分对称点的连线,无从下手,胡乱猜测答案。
【正解】同学们解读题意时,应充分联系轴对称的性质。这里主要是运用“对称轴垂直平分对称点连线”,连接PQ,如图4,可得MN垂直平分PQ。进一步根据垂直平分的性质,连接MP、MQ、NP、NQ,可得MP=MQ,NP=NQ,根据条件,不妨设AP=PD=2a,BQ=a,CQ=3a,AM=x,BM=4a-x,在Rt△AMP与Rt△BMQ中,再利用勾股定理,可得(2a)2+x2=a2+(4a-x)2,解得。同理可得
正确答案
三、变化不全
例3 如图5,矩形ABCD中,AB=4,BC=3,点E是射线CD上的一个动点,把△BCE沿BE折叠,点C的对应点为F。当点F刚好落在线段AB的垂直平分线上时,求CE的长。

图5
【错解】根据折叠,得BF=BC=3,设EF=CE=x,∠F=∠C=90°,过点F作AB的垂线,利用“K字形相似”,可得
【错因】题目条件中“射线”两字很重要,这是一个提示。随着点E沿着CD往左运动,点F可能会落在矩形ABCD的外部,即在AB的上方。
【正解】因为“点E是射线CD上的一个动点”,因此,需以动态的视角去分类讨论。如图6,画图过程中抓住轴对称的根本性质,即BF=BC,得到点F的运动轨迹是以点B为圆心、BC长为半径的圆。再画出AB的垂直平分线与圆的交点,有两个,分别是F1、F2,最后画∠CBF1的角平分线BE1与∠CBF2的角平分钱BE2,即折痕。具体解法与上面错解的解法类似,也是通过构造“K字形相似”,得=

图6
四、理解不透
例4如图7,在△ABC中,∠ACB=90°,AB=18把△ABC绕着点C旋转,使点B与AB边上的点D重合,点A落在点E处,则线段AE的长为( )。
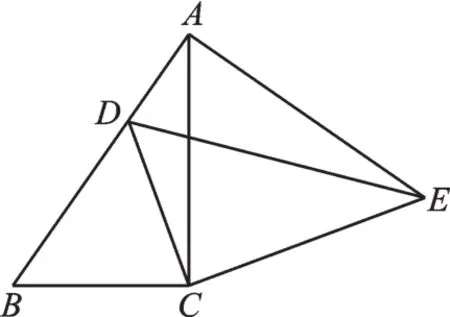
图7

【错解】根据旋转得到对应线段相等,计算得出AC=6,观察图形,选A。
【错因】错解的产生,一是缺少严密的逻辑推理,仅从直观感受得结果;二是没有充分地利用旋转的性质。
【正解】旋转时,旋转角相等这一性质运用广泛。本题中,两个旋转角∠BCD和∠ACE相等,同时由旋转可得BC=DC,AC=EC,由此可得△BCD∽△ACE。再过点C作BD的垂线,求出BD的长度,最后利用相似可求AE的长度。
正确答案:C。
平移、轴对称和旋转是几何中的三种基本变换,我们在解决图形变化的问题时,应当从这三种变换的定义和性质出发,研究变与不变。
