基于改进型滑模观测器与旋转高频电压注入法的永磁同步电机无传感器矢量控制(上)
2019-06-26张家明张利军
张家明,张利军
(中车青岛四方车辆研究所有限公司,山东 青岛 266109)
0 引 言
永磁同步电机的无传感器矢量控制,在中高速段多采用滑模观测器法来实现转子位置估算[1]。使用滑模观测器来实现转子位置估算,可以迫使永磁同步电机的电流的轨迹按照特定的滑模面运动,这个滑模面即为滑动模态,仅仅取决于所选择的切换函数。切换函数多为符号函数,因此当电机的电流的估计值收敛至真实值时会有抖动,这就导致了带载运行时的转矩脉动现象。为了解决这一缺陷,在不改变切换函数的前提下,提出了一种转子位置估算的校正算法,进而可以克服转矩脉动。改进型滑模观测器在低速段,由于电机的定子反电动势较小,估算精度会很低,因此提出了一种旋转高频电压注入法,直接给电机的定子注入旋转高频电压信号,然后电机由于磁路饱和,其定子电流中会包含有转子位置信息,基于设计的解调方法,可以将转子位置精确解算出来,进而实现矢量控制。
1 永磁同步电机的数学模型
在对永磁同步电机进行数学建模时,对电机做以下假设[2]:①定子绕组在空间上是对称的,且定子反电动势是正弦波;②磁链不受温度的影响;③电机的转子磁极是凸极型。
图1为永磁同步电机的矢量坐标,给出了永磁同步电机三相静止abc坐标系、两相静止αβ坐标系和同步旋转dq坐标系的矢量关系。
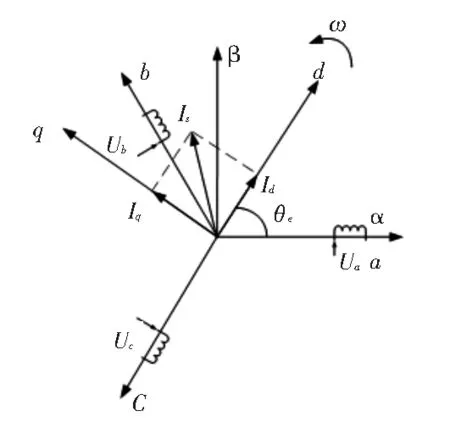
图1 永磁同步电机的矢量坐标
在三相静止abc坐标系下,定子电压方程为
(1)
式中,ua,ub,uc为三相定子电压,V;ia,ib,ic为三相定子电流,A;ψa,ψb,ψc为转子磁链折算到定子侧的三相磁链,Wb;Rs为定子电阻。
以矩阵形式表达式(1),可得:
(2)
在对永磁同步电机进行矢量控制的时候,需要进行Clark变换和Park变换。经过Clark变换得到永磁同步电机在αβ坐标系下的电压方程为
(3)
式中,p为微分算子:uα,uβ为两相静止坐标系下的定子电压,V;iα,iβ为两相静止坐标系下的定子电流,A;ψα,ψβ为两相静止坐标系下,转子磁链折算到定子侧的磁链,Wb。
永磁同步电机在dq坐标系下的电压方程为
(4)
式中,p为微分算子:ud,uq为同步旋转坐标系下的定子电压,V;id,iq为同步旋转坐标系下的定子电流,A;ψd,ψq为同步旋转坐标系下,转子磁链折算到定子侧的磁链,Wb;θr为转子角度,rad/s。
永磁同步电机的矢量控制的本质是在同步旋转dq坐标系下实现转矩和励磁的解耦控制,因此还需要考虑dq坐标系下的磁链方程:
(5)
式中,Ld,Lq为定子dq轴电感,H;ψr为转子磁链,Wb。
永磁同步电机的电磁转矩方程:
Te=np(ψdiq-ψqid)=np[ψfiq+(Ld-Lq)idiq]
(6)
式中,Te为电磁转矩,Nm;np为电机的极对数。
永磁同步电机的运动方程为
(7)
式中,TL为负载转矩,Nm;J为电机的转动惯量;ωr转子电角速度,rad/s。
2 改进型滑模观测器
2.1 滑模观测器的基本原理
如前所述,采用滑模观测器来实现永磁同步电机的转子位置估算,其本质在于通过滑模观测器来估算转子磁链在定子绕组中产生的反电动势[3],进而估算出转子的角度与机械转速。
将滑模观测器的切换函数,也就是滑模面定为S(x)=0,其中,x为系统的状态变量。在PMSM的控制系统中,唯一可以观测的物理量为定子电流,因此将滑模面S(x)的变量x取为定子电流,当系统在滑模面S(x)=0上运动时,定子电流的估算值将收敛于真实值,进而反电动势的估算值也收敛于真实值。图2为滑模观测器的原理图。
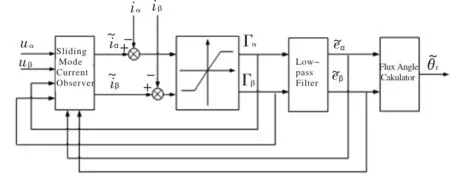
图2 滑模观测器原理图
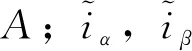
在αβ轴系下的定子电流的状态空间方程为
(8)
式中,Ls为定子电感,其他变量的含义如前所述。
如前所述,将滑模面S(x)的变量x取为定子电流,因此结合式(8)与图2,可得图2中“Sliding Mode Current Observer”,即滑模电流观测器的状态空间表达式为
(9)
式中各变量含义如前所述。实际的工程应用时,需要将式(9)进行离散化处理,转换成差分方程的形式。采用双线性变换法对式(9)进行离散化,可得对应的差分方程为

(10)
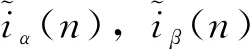
图2中饱和函数的数学表达式为
(11)
式中,Γα,Γβ为饱和函数的αβ轴输出量,V;K1为饱和函数的增益;E0为饱和函数的限幅。
实际的工程应用时,K1的取值范围可以依据实际的转速响应时间来整定,类似于PID控制器的比例增益的整定方法,增大K1可以加快图2中滑模电流观测器的跟踪速度,使得定子电流的观测值尽快收敛于真实值,进而使估算的转子位置尽快跟踪实际的转子位置,减小转速响应时间。E0的作用类似于PID控制器的限幅,需要根据实际的试验效果来确定限幅值。
饱和函数的输出经过图2中一阶低通滤波器“Low-pass Filter”滤波后即可得到反电动势的估算值。图2中一阶低通滤波器的微分方程如式(12)所示:
(12)
式中,ωc为低通滤波器的截止频率,rad/s。
对式(12)进行离散化处理,可得对应的差分方程为
(13)
式中,各变量的含义如前所述。
得到了反电动势的估算值,即可根据式(14)计算转子角度:
(14)
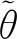
式(14)也就是图2中的“Flux Angle Calculator”。
2.2 基于改进型滑模观测器的矢量控制
如前所述,采用滑模观测器对转子位置进行估算,当电机带载运行时会发生抖动现象。鉴于此,提出了一种转子位置估算的校正算法,用以克服抖动现象。这种校正算法,本质上来说是一种转子位置锁相环,其结构图如图3所示。

图3 转子位置锁相环结构图
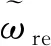
如图3所示,有:
(15)
当定子电流估算值收敛于真实值时,有:
(16)
式中,θr为转子角度真实值,rad;K为反电动势的幅值;联立式(15)、式(16),可得当定子电流估算值收敛于真实值时,有:
(17)
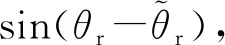
估算出转子位置后,即可根据式(18)计算出转子的机械转速:
(18)
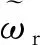
综上所述,基于改进型滑模观测器的永磁同步电机无传感器矢量控制的算法结构图如图4所示。图4中,ωref、IdRef和IqRef分别为转速给定值、定子d轴电流给定值和定子q轴电流给定值;其他变量的含义如前所述。
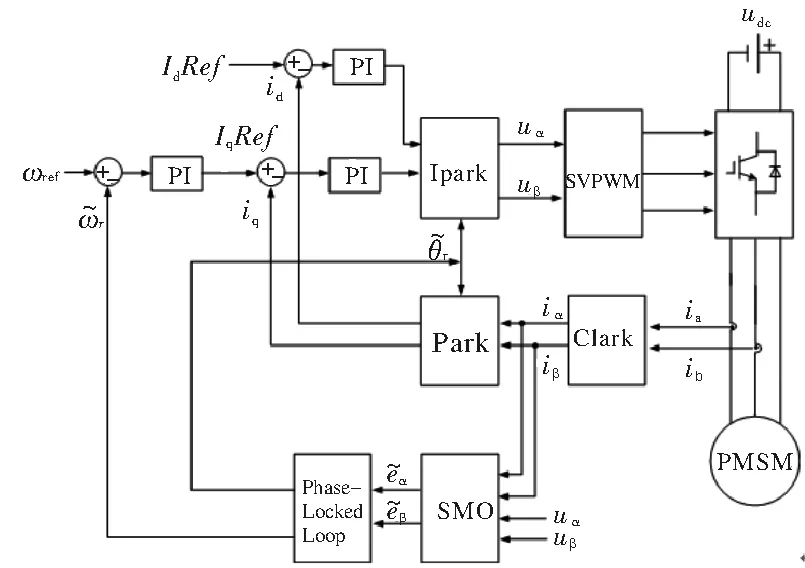
图4 基于改进型滑模观测器的永磁同步电机无传感器矢量控制
3 旋转高频电压注入法
3.1 旋转高频电压注入法的基本原理
当永磁同步电机运转在极低转速段时,由于基波反电动势的幅值过低,导致基于滑模观测器算法进行反电动势估算时,无法使估算的定子电流收敛于真实值,进而估算的反电动势的误差很大,转子位置也就不能正确估算出来[4]。鉴于此,设计了一种旋转高频电压注入法,利用永磁同步电机的磁路饱和特性,向电机定子电压中注入频率远高于基波频率的旋转电压,此时定子基波电压上就叠加了高频电压,定子电流中势必就会含有高频分量。定子电流的高频分量中就包含有转子的位置信息,因此可以通过检测并提取定子电流中的高频分量,再通过一定的解调算法将转子的位置估算出来,进而实现永磁同步电机的无传感器精确转速控制。即便电机带重载运行,也能保证较高的控制精度。
假设高频电压的幅值为ui,角频率为ωi,则注入的高频电压在定子两相静止坐标系(αβ轴系)为
(19)
式中,uαi为定子α轴高频电压,V;uβi为定子β轴高频电压,V;
因为高频电压的频率远远高于基波电压的频率,因此高频电压下的永磁同步电机的数学模型为
(20)
式中,Ls为定子电感,H;iαβi为两相静止坐标系下的定子高频电流,A。
式中,L为平均电感,ΔL为半差电感,其计算公式为
(21)
式中,Ld为定子d轴电感,H;Lq为定子q轴电感,H。
联立式(19)、式(20)、式(21)可得:
(22)
式中,
(23)
式中,ip为定子高频电流的正序分量的幅值,A;in为定子高频电流的负序分量的幅值,A;
由式(22)可知,定子高频电流的负序分量的相位中含有转子位置信息。鉴于此,可以通过提取定子高频电流的负序分量来获取转子电角度θr。
3.2 基于旋转高频电压注入法的矢量控制
图5为基于旋转高频电压注入法的永磁同步电机无传感器矢量控制的算法结构图。
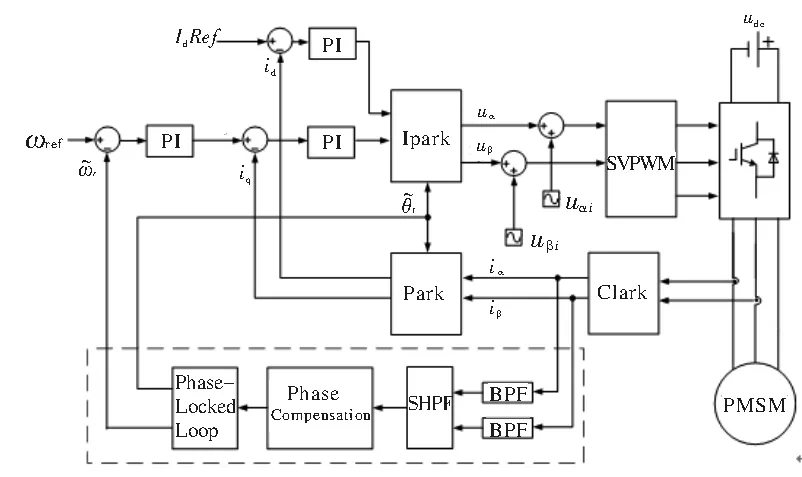
图5 基于旋转高频电压注入法的永磁同步电机无传感器矢量控制
图中,BPF为带通滤波器(Bandpass Filter);SHPF为同步轴系高通滤波器(Synchronous High-pass Filter)。
首先通过BPF,即带通滤波器,将高频电流准确提取出来。然后依据式(22)可知,高频电流正序分量的角频率为ωi,负序分量的角频率为ωi-2ωr。由于ωi>>ωr,故高频电流正序分量的频率与负序分量的频率很接近,普通的低通或高通滤波器不能将两者分离出来,因此设计了SHPF,即同步轴系高通滤波器,用以提取高频电流的负序分量。
本文中,注入的旋转高频电压的频率为500 Hz, BPF为4阶IIR带通滤波器,通带频率为 400~600 Hz,其z域的传递函数为
(24)
图6为BPF滤波器的波特图。幅频特性显示滤波器在500 Hz处的增益为1(0dB),低截止频率为400 Hz,高截止频率为600 Hz。相频特性显示滤波器在500 Hz处的相角几乎为0°,约为-6.4°。因此,使用BPF滤波器对定子电流滤波后,500 Hz高频量幅值无衰减,相位几乎不产生偏差,可准确提取出定子αβ轴系下的高频电流,且α轴高频电流在相位上超前β轴高频电流90°。
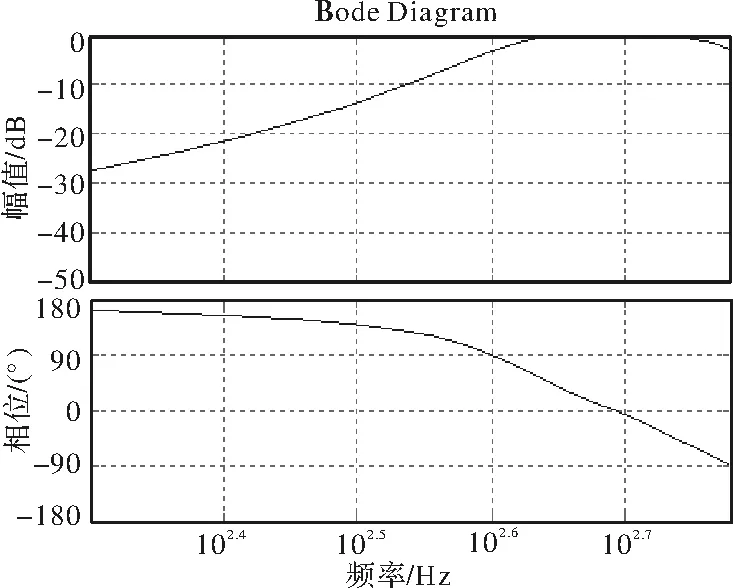
图6 BPF滤波器的波特图
SHPF的实现方式为:首先对αβ轴系下的高频定子电流按照式(25)进行坐标变换,转化为dq轴系下的电流。
(25)
式中,iαi为定子α轴的高频电流,A;iβi为定子β轴的高频电流,A;idi为定子d轴的高频电流,A;iqi为定子q轴的高频电流,A;
进行了一次坐标变换后,高频电流的正序分量表现为直流量,负序分量表现为频率为ωi-2ωr的高频量,再通过高通滤波器滤除直流量,即可得到高频电流的负序分量。SHPF滤波器的实现原理如图7所示[6],图中,θi为高频电流在t时刻的相位。
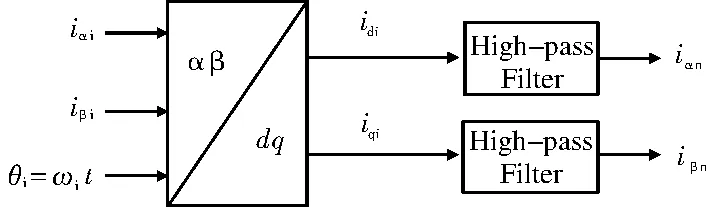
图7 SHPF滤波器的原理框图
图中的iαn和iβn分别为定子α轴高频电流的负序分量和定子β轴高频电流的负序分量,由式(22)可知:
(26)
图7中的高通滤波器,即High-pass Filter的工程实现方式为4阶IIR高通滤波器,波特图如图8所示,幅频特性显示滤波器在0 Hz处的增益要小于-103 dB,截止频率为20 Hz,因此可以有效滤除正序分量。相频特性显示滤波器在ωi-2ωr频率处的相角约为5.9°。
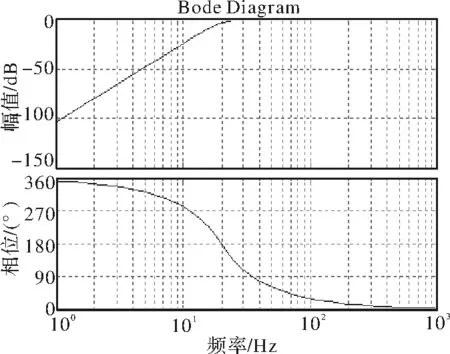
图8 HPF滤波器的波特图
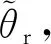
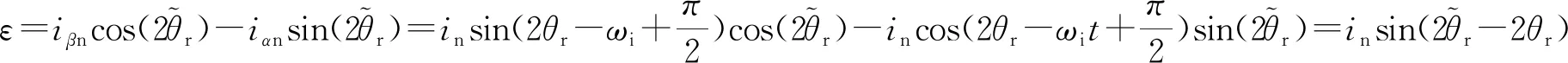
(27)

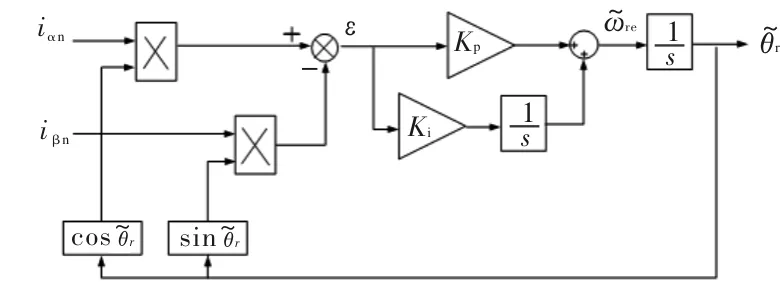
图9 锁相环结构图

(28)
估算出转子位置后,依据式(18)即可计算出电机的机械转速。
